Grundlagen und Entscheidungsrechnungen EwertWagenhofer 2002 Alle Rechte vorbehalten

Ziele n Entscheidungstheoretische Grundlagen zur Lösung von Entscheidungsproblemen n Vereinfachungen, auf denen die traditionelle KLR basiert n Investitionstheoretischer Ansatz der KLR n Verbindungen zwischen dem Kapitalwert auf der Basis von Zahlungen und demjenigen auf der Basis von Kosten und Leistungen 2. 2

Ziele der Entscheidungsträger Optimieren eines Konsumzahlungsstroms – bezüglich seiner Breite, – seiner zeitlichen Struktur – und seiner Unsicherheit Aber Kosten (Leistungen) sind “bewertete, sachzielbezogene Güterverbräuche (Gütererstellungen) eines Unternehmens in einer Periode” Wie paßt das zusammen? 2. 3

Grundmodell der Entscheidungstheorie n n Entscheidungsfeld m Aktionsraum a A m Umweltzustände q Q m Ergebnisfunktion w(a, q) Zielplan m Präferenzsystem Höhenpräferenz m Artenpräferenz m Zeitpräferenz m Risikopräferenz m m Definition der Ergebnisarten 2. 4

Ergebnisfunktion 2. 5

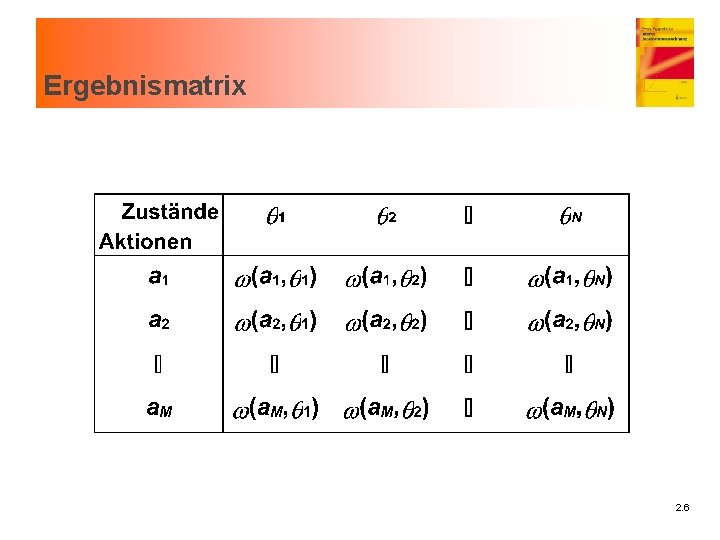
Ergebnismatrix 2. 6

Entscheidungsrechnungen Bereitstellung von Informationen zur zielentsprechenden Lösung von Entscheidungsproblemen n Ermittlung der relevanten Ergebnisstrukturen von Aktionen n Entspricht letztlich der Ergebnismatrix n Kosten I Angesichts eines bestimmten Zielplanes und eines bestimmten Entscheidungsfeldes resultierende negative Konsequenzen einer Aktion Leistungen I Angesichts eines bestimmten Zielplanes und eines bestimmten Entscheidungsfeldes resultierende positive Konsequenzen einer Aktion 2. 7

Notwendigkeit von Vereinfachungen Strenge Anwendung der Prinzipien des Grundmodells läuft auf Totalmodelle hinaus n Weiterhin müßten individuelle Portefeuilleaktivitäten umfassend integriert werden - und zwar bei jedweder Entscheidung n Vorgelagertes Entscheidungsproblem Optimaler Komplexionsgrad eines Planungssystems n Konzeptionen der KLR lassen sich als spezifische Vorschläge zur Lösung des Komplexionsproblems auffassen! 2. 8

Investoren und Unternehmen Unt 1 Arbeitseinkommen Unt 2. . . Untn FI Investor(in) Fin 1 Fin 2 VG Konsum . . . Finm 2. 9

KLR-Konzeption II Aktionsraum: Parameter der institutionalen Unternehmung n Nur finanzielle Ergebnisarten n Alle zeit-zustandsabhängigen Zahlungen werden durch eine spezifische Repräsentanzgröße dargestellt n Kosten II Verringerungen der die ggf. unsicheren, mehrperiodigen monetären Konsequenzen einer Aktion widerspiegelnden Repräsentanzgröße Leistungen II Erhöhungen der die ggf. unsicheren, mehrperiodigen monetären Konsequenzen einer Aktion widerspiegelnden Repräsentanzgröße 2. 10

Repräsentanzgröße n Funktion eines Nutzenwertes n Repräsentanzgröße = Kapitalwert, falls – vollkommener Kapitalmarkt – sichere Erwartungen n Bei unsicheren Erwartungen Marktwert, falls – Spanning – Competitivity n Separationstheorem Bestimmung der optimalen Entscheidungen der Unternehmung kann unabhängig von den individuelllen Konsum- bzw. Portefeuilleentscheidungen durchgeführt werden 2. 11

Investitionstheoretischer Ansatz der KLR Darstellung anhand zweier Beispiele n Intertemporal optimale Produktionsstrategien n “Traditionelle” Kosten als Spezialfälle 2. 12

Optimale Produktionsstrategien auf investitionstheoretischer Basis n Zielgröße Maximierung des Kapitalwertes 2. 13

Intertemporal optimale Produktion Annahmen (1) Nutzungsdauer liegt fest n Kapitalwert der laufenden Einzahlungen: KWe n Kapitalwert der laufenden Auszahlungen: KWa n KW = KWe - KWa - I n Investitionstheoretische Kosten und Leistungen Kosten Erhöhungen des Kapitalwertes der Auszahlungen inklusive der Investitionsauszahlungen Leistungen Erhöhungen des Kapitalwertes der Einzahlungen 2. 14

Intertemporal optimale Produktion Annahmen (2) n Zu bestimmen: Produktionsstrategie xt (t = 1, . . . , T) Erlöszusammenhänge: Preisabsatzfunktion pt(xt) n Annahme: Keine zeitlichen Interdependenzen bei Erlösen Daher: Auszahlungsseite im Mittelpunkt n Erlöse: 2. 15

Fall 1: Keine zeitlichen Auszahlungsinterdependenzen Zusammenhänge im Auszahlungsbereich 2. 16

Optimierung im Fall 1 Kapitalwert KW Addition diskontierter, unverbundener Überschüsse Optimierungsbedingungen „ Grenzerlös = Grenzkosten “ 2. 17

Fall 2: Bestehende Interdependenzen Lerneffekte n Verschleißeffekte n Auszahlungen: At = At(x 1, x 2, . . . , xt) n n Präzisierung durch Änderungsfaktoren ct(xt): – ct(0) = 0 (Normierung) – ct´(xt) < 0 bei Lerneffekten – ct´(xt) > 0 bei Verschleißeffekten n Auszahlungen z. B für t = 4: 2. 18

Auszahlungen und Änderungsfaktoren n Beispiel: Optimierung für t = 1 Gegebene Produktionsmengen für t = 2, . . . , T 2. 19

Auszahlungen in Folgeperioden Grenzkosten 2. 20

Intertemporale Effekte n “Reiner” Periodeneffekt Grenzkosten ohne zeitliche Interdependenzen n “Dynamischer” Effekt Veränderung der künftigen Auszahlungen durch Variation der heutigen Produktion Bedingungen für die jetzt optimale Menge in t = 1 2. 21

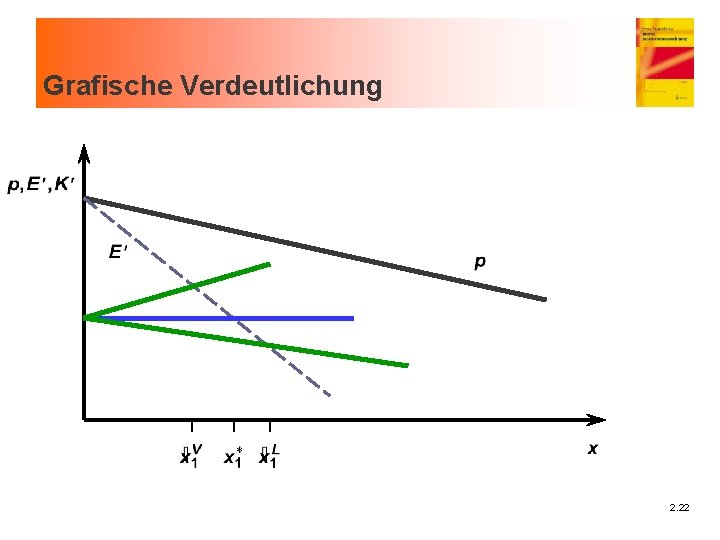
Grafische Verdeutlichung 2. 22

Konsequenzen in Fall 2 n Lerneffekt Investition in Erfahrung “Überproduktion” n Verschleißeffekt – “Unterproduktion” Probleme n Woher stammen die künftigen Mengen für t = 2, . . . , T? n Annahme: Langfristig optimaler Plan liegt vor n Müßten dafür aber nicht analoge Zusammenhänge wie für t = 1 gelten? n Führt erneut auf Totalmodelle 2. 23

Beispiel - Annahmen n Zweiperiodiges Problem Zinssatz i = 0, 25 Gleiche Preis-Absatz-Funktionen für beide Perioden pt(xt) = p(xt) = 100 - 2 xt Keine fixen Periodenauszahlungen Variable Stückauszahlungen k 1 = k 2 = 20 Investitionsauszahlung I = 700 Verschleißeffekt c(x 1) = 0, 1 x 1 2. 24

Statische Optimierung Erlöse : 100 x - 2 x 2 Grenzerlöse 100 - 4 x Grenzkosten 20 Bedingung 1. Ordnung Zahlungsüberschuss 100 • 20 - 2 • 202 - 20 • 20 = 800 Kapitalwert 2. 25

“Dynamische” Optimierung via Gleichungssystem (1) Zinssatz wird vorerst allgemein berücksichtigt Kapitalwert Bedingungen 1. Ordnung 2. 26

Dynamische Optimierung via Gleichungssystem (2) Einsetzen in die erste Bedingung ergibt 2. 27

Einfluß höherer Zinssätze Verschleißeffekt Lerneffekt m Höhere Menge in t = 1 m Geringere Menge in t = 1 m Höherer Überschuß Ü 1 m Geringere Menge in t = 2 m Geringerer Überschuß Ü 2 m Niedrigerer Kapitalwert und umgekehrt für niedrigere Zinssätze 2. 28

Traditionelle Kosten als Spezialfälle n Illustration Entwicklung linearer Abschreibungen aus dem investitionstheoretischen Ansatz Lineare Abschreibungen: Ab = (I - LQ)/T Annahmen Unendliche, identische Investitionskette m Betrachtung nur der Auszahlungsseite m Bestimmung eines “Anlagenwertes”, dessen zeitliche Veränderung die investitionstheoretischen Abschreibungen ergibt m Vergleich der Auszahlungskapitalwerte neuer Aggregate mit denjenigen gebrauchter Anlagen m 2. 29

Wert einer Anlage KWa ( ) Kettenkapitalwert für eine gebrauchte Anlage mit der Nutzungsdauer t = 0, . . , T-1 2. 30

Wert einer vorhandenen Anlage n Eigenschaften – W(0) = I – W(T) = LQ 2. 31

Abschreibungen Ab(t) n Summe aller Abschreibungen 2. 32

Bedingungen für lineare Abschreibungen 1. Konstante laufende Auszahlungen Kettenkapitalwert 2. Vernachlässigbarer Zinssatz Abschreibungen 2. 33

Fazit zur Abschreibungsproblematik Traditionelle Vorgehensweise Vergangenheitsorientiert n Verteilung der Ausgaben gemäß “Güterverzehr” n Investitionstheoretische Vorgehensweise Zukunftsorientiert n Wertänderungen setzen sich nur aus künftigen Zahlungen zusammen n Korrespondenz durch Annahme unendlicher, identischer Kette 2. 34

Traditionelle KLR (Konzeption III) Kosten III (Leistungen III) Bewertete, sachzielbezogene Güterverbräuche (Gütererstellungen) eines Unternehmens in einer Periode Verbindungen zur Konzeption II • Eingrenzung auf institutionale Unternehmung • Monetäre Natur Unterschiede zur Konzeption II • Periodisierung von Zahlungen nach Maßgabe von “Güterverbrauch” und “Gütererstellung” • Vorwiegend empfohlene Anwendung im Rahmen sogenannter “kurzfristig wirksamer Entscheidungen” 2. 35

Fristigkeit von Entscheidungsproblemen Separierung von Entscheidungsfeldern Langfristig und kurzfristig wirksame Entscheidungen n Begründbar, falls n – keine zeitlichen Interdependenzen im Zahlungsbereich – keine zeitlichen Interdependenzen im Restriktionsbereich – alle Zahlungswirkungen der operativen Aktivitäten einer Periode in dieser Periode n Faktisches Kriterium Bestand an Potentialfaktoren ändert sich nicht bei einer bestimmten Entscheidung Das sind letztlich aber unterschiedliche Sachverhalte 2. 36

Güterverbräuche und Gütererstellungen n Erklärbar aus zeitlichen Verwerfungen von – Einzahlungen, Leistungen – Auszahlungen, Kosten n Kriterium ist das Auslösen von Zahlungen durch Maßnahmen der laufenden Periode n Berücksichtigung von Zinseffekten – Zinsen auf das durchschnittlich gebundene Kapital 2. 37

Kurzfristig wirksame Entscheidungen Beispiele n Beschaffungsbereich – Beschaffungsmengen, -wege und Bezugsquellen – Preisobergrenzen n Produktionsbereich – Produktionsprogramme und -verfahren – Losgrößen und Sortenschaltung – Zusatzaufträge n Absatzbereich – Preisuntergrenzen, Absatzpreise und Absatzlager – Vertriebswege, Verkaufsgebiete, Kundengruppen n Integrative Bereiche – Fertigungstiefe (“Make or Buy”) – Verrechnungspreise – innerbetriebliche Logistik 2. 38

Angleichung von interner und externer Unternehmensrechnung? Vorteile n International keine strikte Trennung gebräuchlich n Kostengünstiger n Angleichung von Controllingund Reporting-Systemen n Orientierung an gegebenen Regeln und oftmals externe Prüfung der Zahlen Nachteile n Probleme bei Erfüllung der Funktionen (“Different Costs for different purposes”) n Oftmals ungeeignete Bilanzierungsregeln n Für Planungszwecke werden Plangrößen benötigt n Ansatz von Opportunitätskosten nicht ohne weiteres möglich 2. 39

Verbindung zu langfristig wirksamen Entscheidungen - Beispiel Projekt mit Investitionsauszahlung I = 1. 000 Nutzungsdauer T = 2, Zinssatz i = 0, 1 Zahlungsüberschüsse z 1 = 550, z 2 = 605 Kapitalwert KW = -1. 000 + 550/1, 1 + 605/1, 21 = 0 Lineare Abschreibung Ab 1 = Ab 2 = 500 Gewinne G 0 = 0 G 1 = 550 - 500 = 50 G 2 = 605 - 500 = 105 Barwert der Gewinne 0 + 50/1, 1 + 105/1, 21 = 123, 23 2. 40

Lücke-Theorem Kapitalbindung n Kapitalbindung KBt Differenz der bis zum Zeitpunkt t kumulierten Gewinne und der kumulierten Zahlungsüberschüsse oder 2. 41

Lücke-Theorem n Voraussetzung: Kongruenzprinzip Clean Surplus Condition n Residualgewinn 2. 42

Implikationen des Lücke-Theorems n n n Grundlage für eine Entscheidungsrechnung, die auf alle Probleme anwendbar ist Diskontierung von Residualgewinnen, Korrektur der Zinsverzerrungen Verwendungsmöglichkeiten im Rahmen der Investitionskontrolle und absoluter Vorteilhaftigkeit Formelle, nicht materielle Bedeutung Kenntnis der künftigen Politik erforderlich Residualgewinne können zu Anreizkompatibilität führen, wenn Prämie Pt daran geknüpft wird Siehe dazu auch 10. Kapitel Economic Value Added 2. 43

Clean-Surplus-Accounting (CSA) und Lücke-Theorem n CSA basiert auf Clean-Surplus-Relation (CSR) CSA umfasst das Kongruenzprinzip Erfasst auch direkte Eigenkapitalbuchungen (other comprehensive income) n Analog zum Lücke-Theorem gilt bei CSR für den Marktpreis 2. 44