Growth Mixture Model Latent Variable Modeling and Measurement

Growth Mixture Model Latent Variable Modeling and Measurement Biostatistics Program Harvard Catalyst | The Harvard Clinical & Translational Science Center Short course, October 28, 2016 Slides contributed by Jeannie-Marie Leoutsakos, Assistant Professor of Psychiatry & Mental Health, Johns Hopkins University

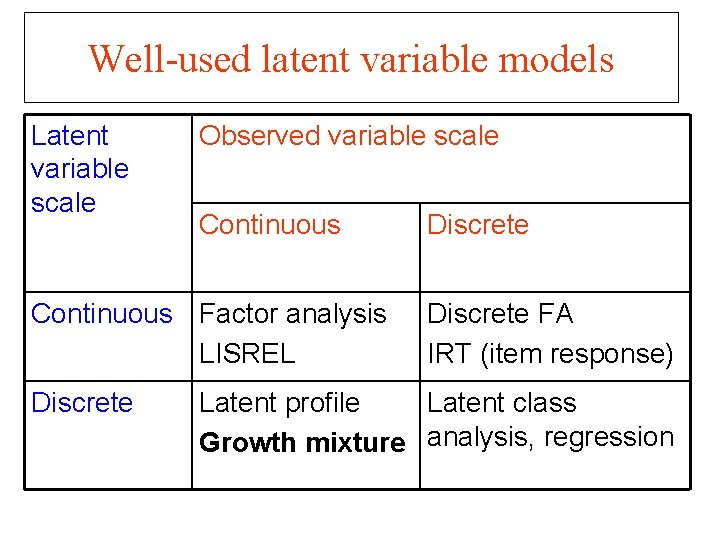
Well-used latent variable models Latent variable scale Observed variable scale Continuous Factor analysis LISREL Discrete FA IRT (item response) Latent profile Latent class Growth mixture analysis, regression

Outline • Motivating Example: The ADAPT trial • Two Options for Modeling Heterogeneity 1. Mixed Effects/Growth Curve Models 2. Growth Mixture Models • Comparison of Options & Final Thoughts

AD and Inflammation • AD characterized by β-amyloid plaques and neurofibrillary tangles • AD is progressive, with a long preclinical period. • Inflammatory processes have been linked to plaque and tangle formation • Inflammatory processes also linked to clearance of β-amyloid.

AD and NSAIDs • In observational studies, NSAID use associated with reduced risk of AD • AD treatment trials show no effect of NSAIDs • In an MCI prevention trial, NSAID increased risk.

The ADAPT Trial • Multi-site prevention trial N=2528 • Participants 70+, family history of AD • 200 mg of celecoxib bid, 220 mg of naproxen sodium bid, or matching placebo (1: 1: 1. 5) • Enrollment began in 2001, halted December 2004 due to safety concerns. • Study cohort is still being followed.

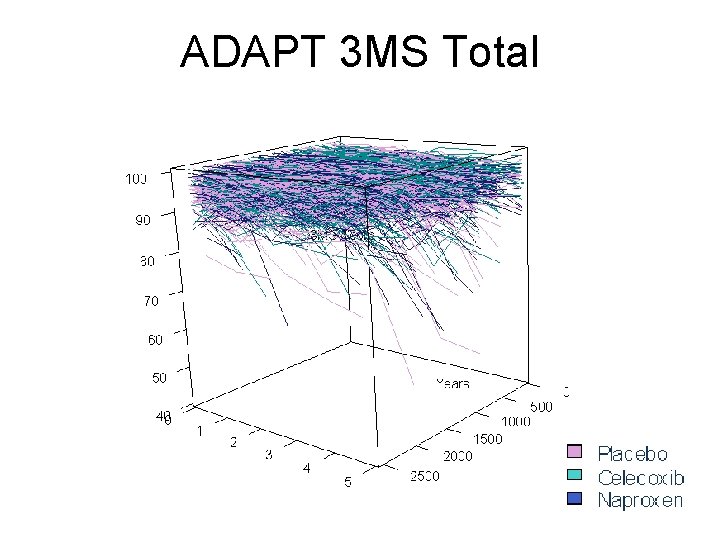
ADAPT 3 MS Total

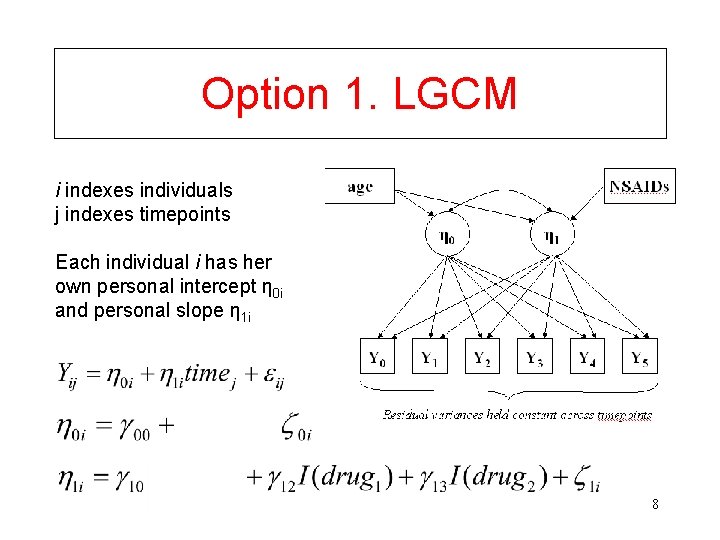
Option 1. LGCM i indexes individuals j indexes timepoints Each individual i has her own personal intercept η 0 i and personal slope η 1 i 8

Option 1. Mixed Effects Model β 1 tij +β 5 nap·tij β 0+b 0 i β 0 β 1 tij+ b 1 itij β 1 tij 3 MS β 1 tij + β 3 cel·tij time Yij= 00+ + 0 i+ 10 tij+ +b 1 i 1 ittiji ++ 12 cel·tijij++ 13 nap·tijij+ε +εijij 12 cel·t 13 nap·t

SAS Syntax • Random Intercept + Random Slope Model proc mixed data = adapt method=ml covtest; model h=time agec drug 1 drug 2 time*drug 1 time*drug 2 /s; random int time/ type = un sub = id; run; Model Random Effects 10

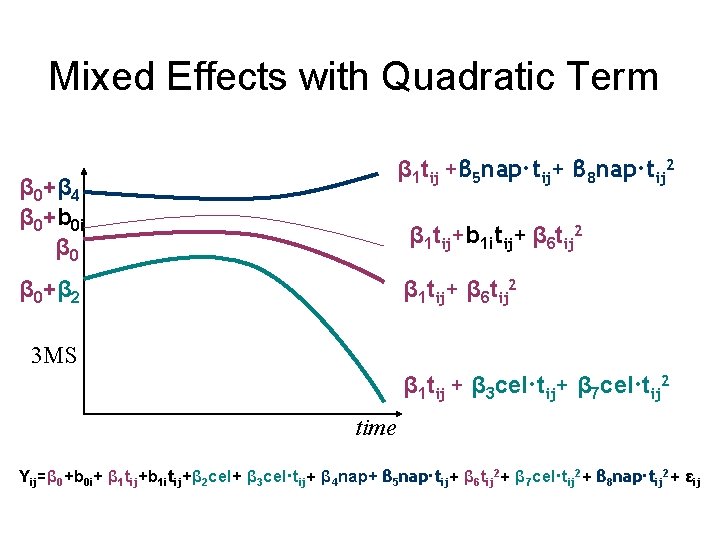
Mixed Effects with Quadratic Term β 1 tij +β 5 nap·tij+ β 8 nap·tij 2 β 0+β 4 β 0+b 0 i β 0 β 1 tij+b 1 itij+ β 6 tij 2 β 1 tij+ β 6 tij 2 β 0+β 2 3 MS β 1 tij + β 3 cel·tij+ β 7 cel·tij 2 time Yij=β 0+b 0 i+ β 1 tij+b 1 itij+β 2 cel+ β 3 cel·tij+ β 4 nap+ β 5 nap·tij+ β 6 tij 2+ β 7 cel·tij 2+ β 8 nap·tij 2+ εij

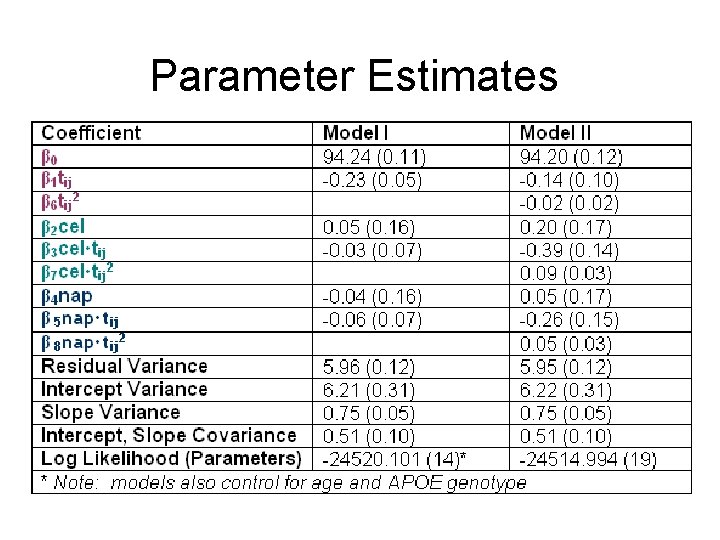
Parameter Estimates

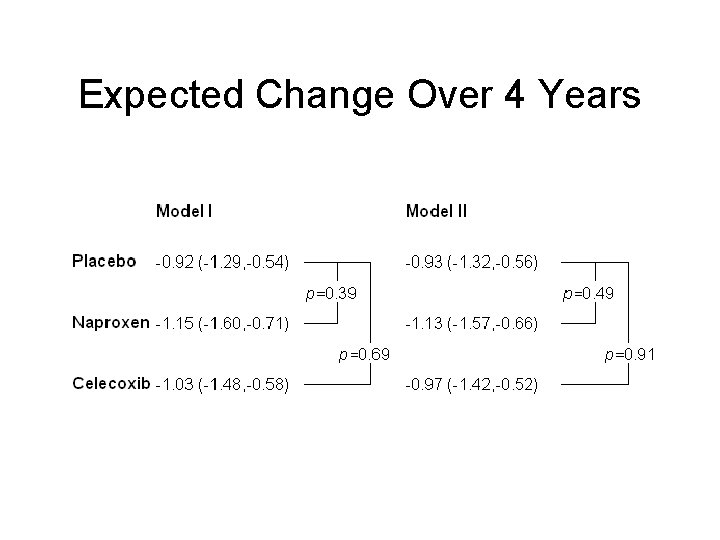
Expected Change Over 4 Years

Observed and Predicted Trajectories Model II

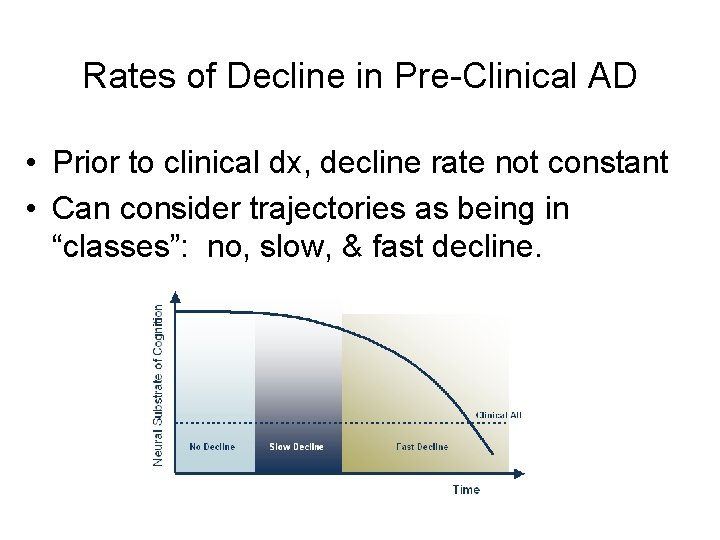
Rates of Decline in Pre-Clinical AD • Prior to clinical dx, decline rate not constant • Can consider trajectories as being in “classes”: no, slow, & fast decline.

The Timing Hypothesis • Contradiction between observational and clinical trials due to differences in timing of exposure to NSAIDs • Early/little or no decline: NSAIDs good • Later/ substantial decline: NSAIDs bad • Observational trials: most individuals in no/slow decline class when exposed • Clinical trials: larger proportion of individuals in the fast decline class

Testing the Timing Hypothesis • Ideal: Stratify individuals by decline class, fit mixed effects models with NSAID effects separately for each class. • Problem: we don’t know for sure how many classes there are, or who is in each class. Class is a latent variable.

Mixed Effects Models as “Growth Models” • Term used in developmental research • “Growth” – getting taller, smarter, etc. • Fixed effects (intercept, slope, quadratic) referred to as “Growth Factors”

Mixture Models • Useful when you believe your population is actually a mixture of subpopulations. • “Mixture” here has nothing to do with “Mixed Effects”

Option 2. Growth Mixture Models • Allows for the estimation of a prespecified number of latent classes of trajectories – Determined via a combination of substantive theory, fit indices, and bootstrapped likelihood ratio tests. • Estimates mixed effects model (growth model) parameters for each latent class

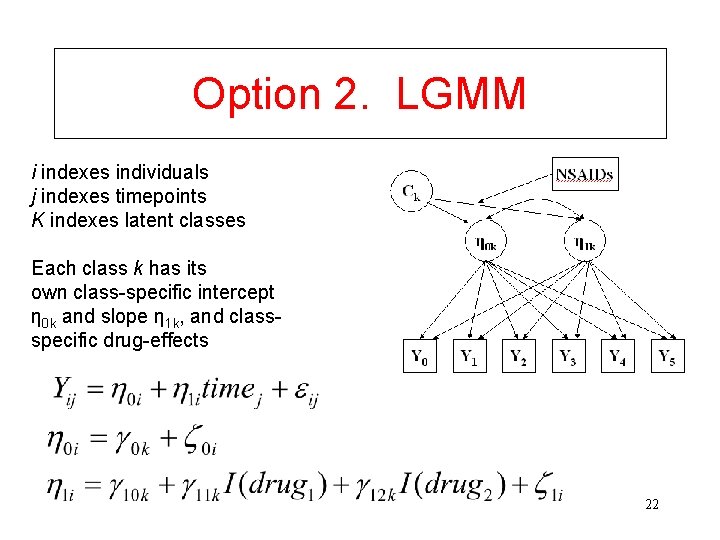
Option 2. LGMM i indexes individuals j indexes timepoints K indexes latent classes Each class k has its own class-specific intercept η 0 k and slope η 1 k, and classspecific drug-effects 22

Growth Mixture Model Parameters • For each class (indexed by k), we now have Yij= 0 k+ 0 i+ 10 ktij+ 1 itij+ 11 kcel·tij+ 12 knap·tij+εij • Simultaneously, model probability of membership in each class via multinomial logistic regression - this allows for inclusion of predictors of class membership (e. g. , age, such that older individuals have greater probability of membership in the fast-decline class.

Step 1. for LGMM Single-class LGCM (no covariates) • Assess variability of intercepts and slopes (graphically) • Determine whether a quadratic term is needed. • Assess the correlation structure among outcomes across time. (eg, is it OK to hold residual variance of Ys constant over time? ). 24

Step 2. For LGMM Fit Latent Class Growth Analyses • Unlike GMM, var(I) and var(S) is fixed at 0. • Using the same methods as with LCA (BIC and BLRT) determine the appropriate number of classes • Do this with and without covariates 25

MPLUS Input for LCGA Specify latent classes Fix I and S variances Estimate I and S separately for each class 26

MPLUS Input for BLRT one set of start values for parameter estimation Specify # of starts for BLRT Ask for BLRT 27

Choosing Number of Classes Without covariates (and with, not shown) a two-class model does not fit the data as well as a three-class model 28

Step 3. Fit GMM • First with class invariant I, S variances • Also possible to have class-varying I, S variances • Add covariates • Ponder meaning 29

Class-Invariant I S Variances 30

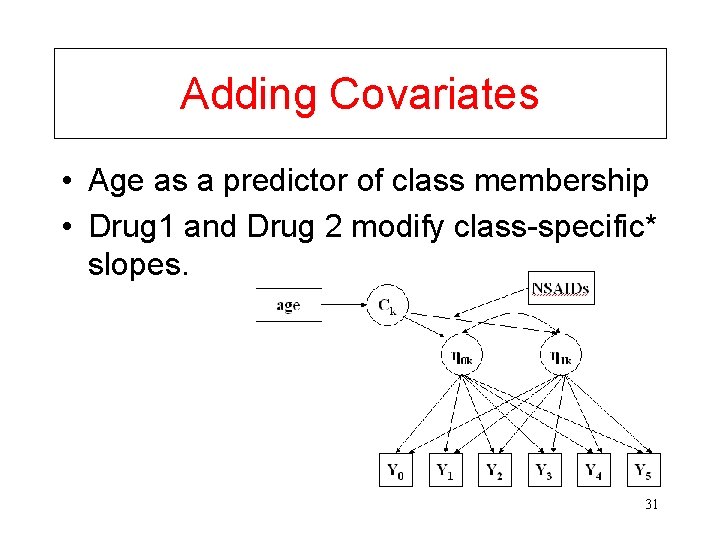
Adding Covariates • Age as a predictor of class membership • Drug 1 and Drug 2 modify class-specific* slopes. 31

GMM with Covariates Input 32

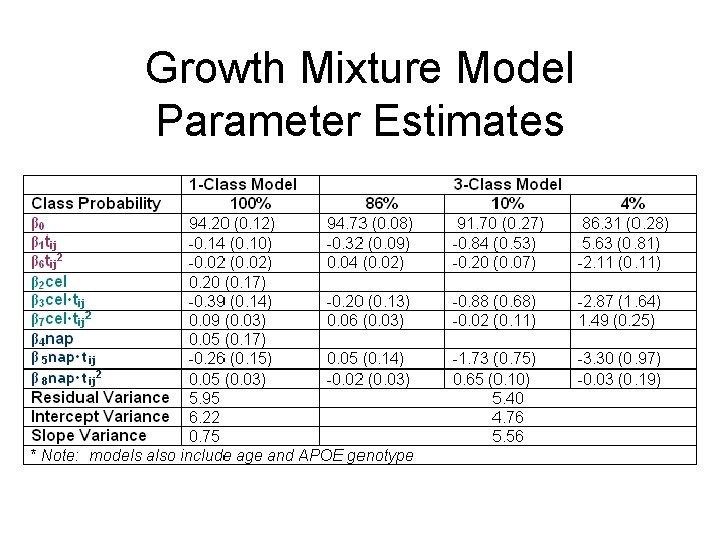
Growth Mixture Model Parameter Estimates

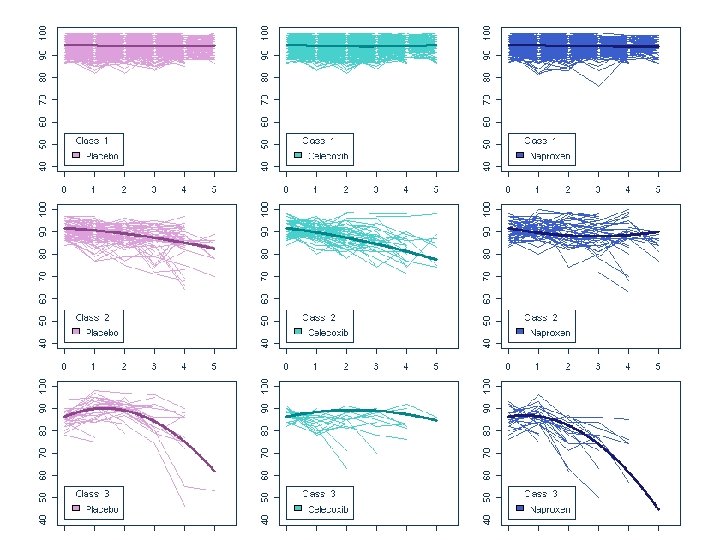
Expected Change Over Time A model where drug effects are forced to be the same across classes fits the data significantly worse (-2 LLD: 369. 23; p<0. 001)

Comparison of Options Mixed Effects • Assumes one population • Simpler interpretation • More parsimonious • Standard software • Results can be more definitive Growth Mixture Model • Models subpopulations • Complex interpretation • More parameters • Need larger sample • Need $pecial $oftware • Results not definitive; post-hoc subgroup analysis

Final Thoughts on Growth Mixture Models • What does it all mean? • possible to get fit indices, etc which support a multi-class mixture when really there are no underlying subgroups. • Entails a number of assumptions about the within-person correlation and random effects, results can be highly sensitive to those assumptions • Assumptions/model fit difficult to check • Hypothesis generating/refining rather than confirming.