GROWTH AND DECAY Section 6 2 Calculus APDual












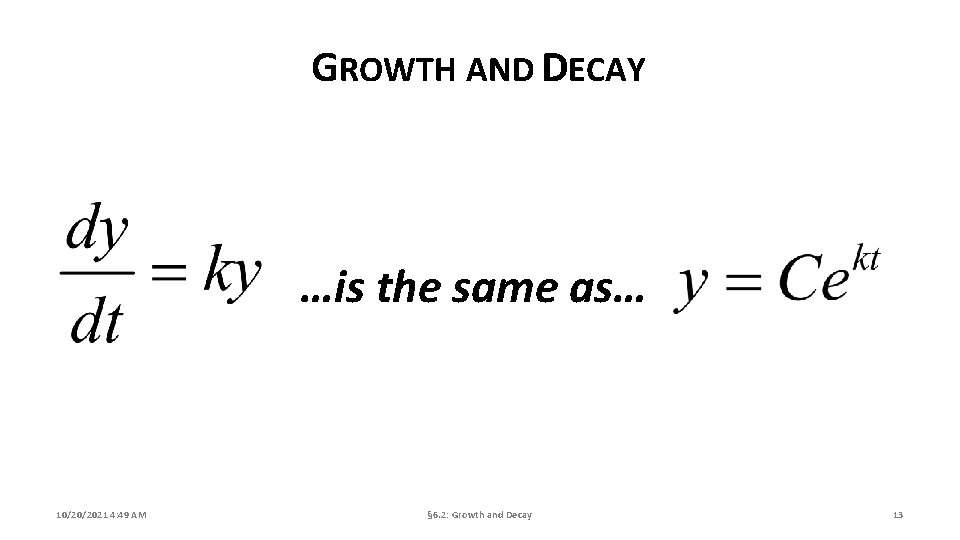










![CALCULATOR INSTRUCTION A. [2 nd] [+] [7] [1] [2] to ensure clarity B. ALWAYS CALCULATOR INSTRUCTION A. [2 nd] [+] [7] [1] [2] to ensure clarity B. ALWAYS](https://slidetodoc.com/presentation_image_h2/d590822fa3e356cbcaa752b1d2b010c9/image-24.jpg)











- Slides: 36

GROWTH AND DECAY Section 6. 2 Calculus AP/Dual, Revised © 2018 viet. dang@humbleisd. net 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 1

REVIEW 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 2

ALGEBRA REVIEW 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 3

EXAMPLE 1 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 4

EXAMPLE 2 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 5

EXAMPLE 2 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 6

EXAMPLE 3 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 7

YOUR TURN 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 8

GROWTH AND DECAY 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 9

GROWTH AND DECAY 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 10

GROWTH AND DECAY 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 11

EQUATION 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 12
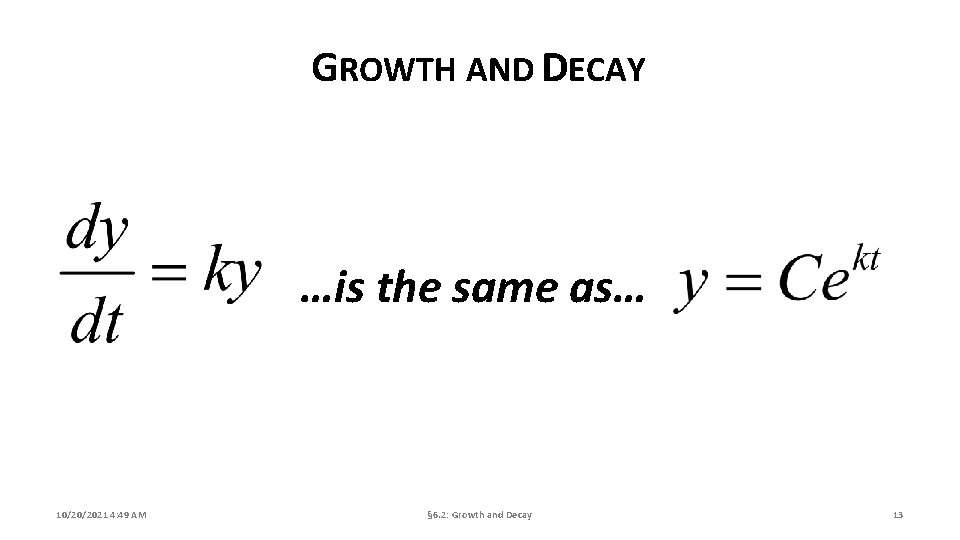
GROWTH AND DECAY …is the same as… 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 13

STEPS 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 14

EXAMPLE 4 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 15

EXAMPLE 4 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 16

EXAMPLE 4 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 17

EXAMPLE 4 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 18

EXAMPLE 5 During a certain epidemic, the number of people that are infected at any time increases at a rate proportional to the number of people that are infected at that time. If 1, 000 people are infected when the epidemic is first discovered, and 1, 200 are infected 7 days later, then write the equation where there are 12 days after the epidemic is first discovered. 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 19

EXAMPLE 5 During a certain epidemic, the number of people that are infected at any time increases at a rate proportional to the number of people that are infected at that time. If 1, 000 people are infected when the epidemic is first discovered, and 1, 200 are infected 7 days later, then write the equation where there are 12 days after the epidemic is first discovered. 10/20/2021 4: 49 AM § 6. 2: Growth and Decay 20

EXAMPLE 5 During a certain epidemic, the number of people that are infected at any time increases at a rate proportional to the number of people that are infected at that time. If 1, 000 people are infected when the epidemic is first discovered, and 1, 200 are infected 7 days later, then write the equation where there are 12 days after the epidemic is first discovered. 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 21

EXAMPLE 5 During a certain epidemic, the number of people that are infected at any time increases at a rate proportional to the number of people that are infected at that time. If 1, 000 people are infected when the epidemic is first discovered, and 1, 200 are infected 7 days later, then write the equation where there are 12 days after the epidemic is first discovered. 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 22

EXAMPLE 5 During a certain epidemic, the number of people that are infected at any time increases at a rate proportional to the number of people that are infected at that time. If 1, 000 people are infected when the epidemic is first discovered, and 1, 200 are infected 7 days later, then write the equation where there are 12 days after the epidemic is first discovered. 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 23
![CALCULATOR INSTRUCTION A 2 nd 7 1 2 to ensure clarity B ALWAYS CALCULATOR INSTRUCTION A. [2 nd] [+] [7] [1] [2] to ensure clarity B. ALWAYS](https://slidetodoc.com/presentation_image_h2/d590822fa3e356cbcaa752b1d2b010c9/image-24.jpg)
CALCULATOR INSTRUCTION A. [2 nd] [+] [7] [1] [2] to ensure clarity B. ALWAYS in radian mode, NEVER in degree mode C. Round decimal answers to 4 DECIMAL places. DO NOT round the third number of a decimal answer. 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 24

EXAMPLE 6 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 25

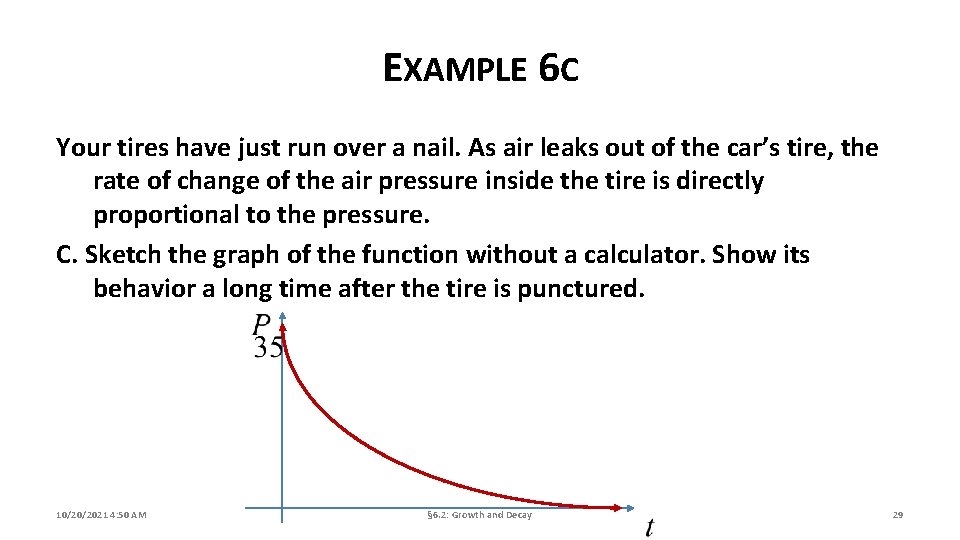
EXAMPLE 6 A Your tires have just run over a nail. As air leaks out of the car’s tire, the rate of change of the air pressure inside the tire is directly proportional to the pressure. A. Write a differential equation that states this fact. Evaluate the proportionality constant if, at the time of zero, the pressure is 35 psi and decreasing at a rate of. 28 psi/min. 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 26

EXAMPLE 6 B 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 27

EXAMPLE 6 B 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 28

EXAMPLE 6 C Your tires have just run over a nail. As air leaks out of the car’s tire, the rate of change of the air pressure inside the tire is directly proportional to the pressure. C. Sketch the graph of the function without a calculator. Show its behavior a long time after the tire is punctured. 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 29

EXAMPLE 6 D Your tires have just run over a nail. As air leaks out of the car’s tire, the rate of change of the air pressure inside the tire is directly proportional to the pressure. D. What would the pressure be 10 minutes after the tire was punctured? 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 30

EXAMPLE 6 E Your tires have just run over a nail. As air leaks out of the car’s tire, the rate of change of the air pressure inside the tire is directly proportional to the pressure. E. The car is safe to drive as long as the tire pressure is 12 psi or greater. For how long after the puncture will the car be safe to drive? 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 31

AP MULTIPLE CHOICE PRACTICE QUESTION 1 (NON-CALCULATOR) 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 32

AP MULTIPLE CHOICE PRACTICE QUESTION 1 (NON-CALCULATOR) Vocabulary 10/20/2021 4: 50 AM Connections and Process § 6. 2: Growth and Decay Answer and Justifications 33

AP MULTIPLE CHOICE PRACTICE QUESTION 2 (NON-CALCULATOR) 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 34

AP MULTIPLE CHOICE PRACTICE QUESTION 2 (NON-CALCULATOR) Vocabulary 10/20/2021 4: 50 AM Connections and Process § 6. 2: Growth and Decay Answer and Justifications 35

ASSIGNMENT Worksheet 10/20/2021 4: 50 AM § 6. 2: Growth and Decay 36