Group theory Group Definition A group is a

Group theory

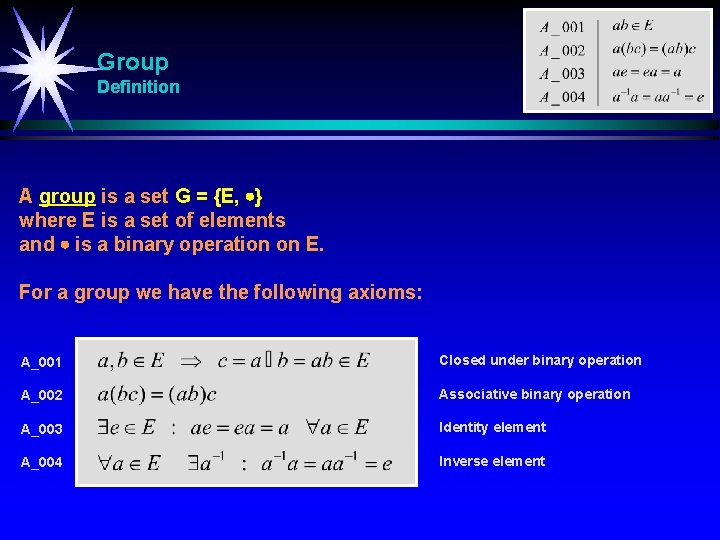
Group Definition A group is a set G = {E, } where E is a set of elements and is a binary operation on E. For a group we have the following axioms: A_001 Closed under binary operation A_002 Associative binary operation A_003 Identity element A_004 Inverse element

Identity element Uniqueness T_001 A group have only one identity element Proof:

Inverse element Uniqueness T_002 An element has only one inverse Proof:

Invers element (a-1)-1 = a T_003 The inverse of the inverse of an element is the element itself (a-1)-1 = a Proof:

Identity element Its own inverse T_004 The identity element is its own inverse e-1 = e Proof:

Inverse of a product T_005 The inverse of a product is the product of the inverse in reverse order (ab)-1 = b-1 a-1 Proof:

Inverse of a product T_005 The inverse of a product is the product of the inverse in reverse order (ab)-1 = b-1 a-1 Proof:

Summing up A_001 A_002 A_003 A_004 T_001 T_002 T_003 T_004 T_005

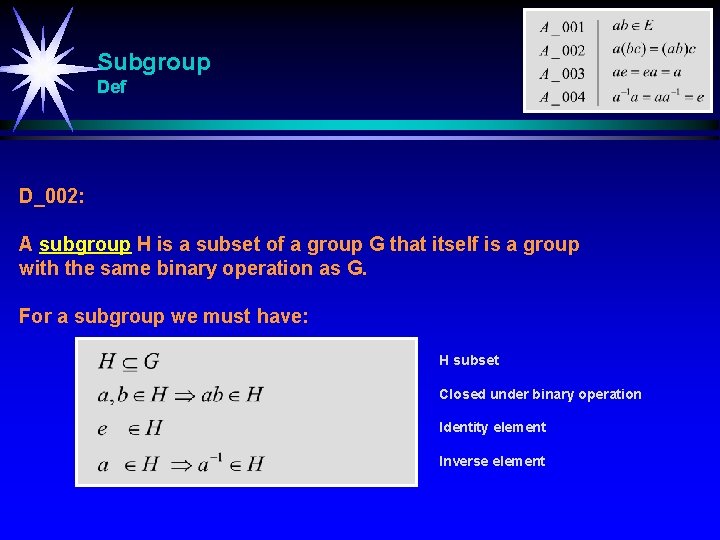
Subgroup Def D_002: A subgroup H is a subset of a group G that itself is a group with the same binary operation as G. For a subgroup we must have: H subset Closed under binary operation Identity element Inverse element

Subgroup Theorem T_006: A subset H is a subgroup if and only if ab-1 H for all a, b H. Proof:

Group Example - Number G E a b ab e a -1 Undergruppe av

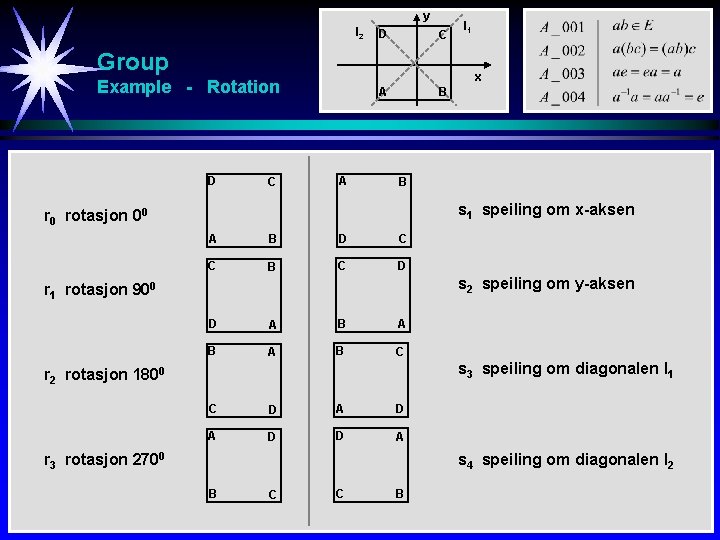
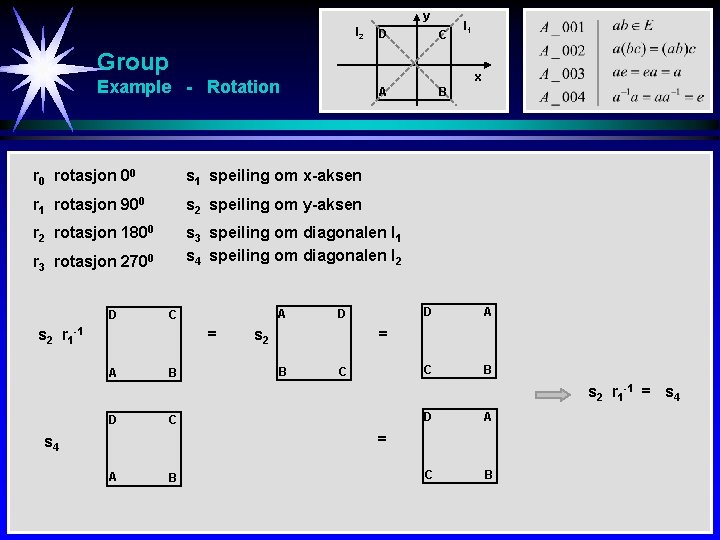
y l 2 D C Group x Example - Rotation D C l 1 A A B B s 1 speiling om x-aksen r 0 rotasjon 00 A B D C C B C D s 2 speiling om y-aksen r 1 rotasjon 900 D A B A B C s 3 speiling om diagonalen l 1 r 2 rotasjon 1800 C D A D D A r 3 rotasjon 2700 s 4 speiling om diagonalen l 2 B C C B

y l 2 D C Group x Example - Rotation A r 0 rotasjon 00 s 1 speiling om x-aksen r 1 rotasjon 900 s 2 speiling om y-aksen r 2 rotasjon 1800 s 3 speiling om diagonalen l 1 s 4 speiling om diagonalen l 2 r 3 rotasjon 2700 D A C s 2 r 1 -1 = A B l 1 D s 2 B D A C B = B C s 2 r 1 -1 = s 4 D C D A C B = s 4 A B

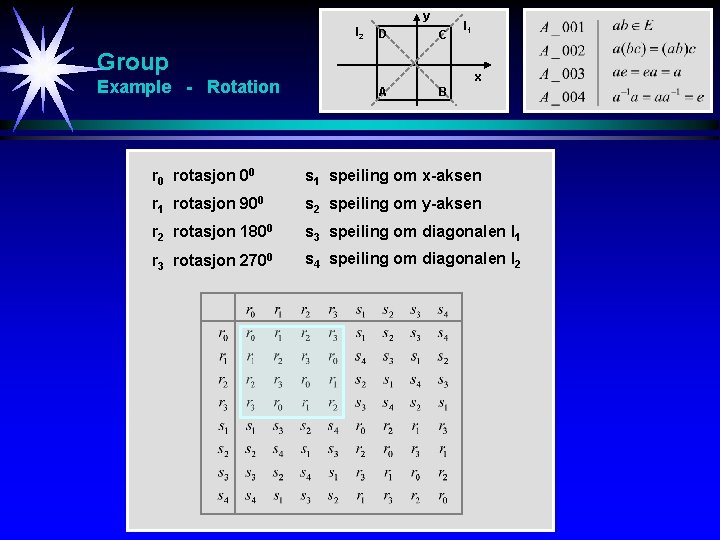
y l 2 D C Group Example - Rotation l 1 x A B r 0 rotasjon 00 s 1 speiling om x-aksen r 1 rotasjon 900 s 2 speiling om y-aksen r 2 rotasjon 1800 s 3 speiling om diagonalen l 1 r 3 rotasjon 2700 s 4 speiling om diagonalen l 2

END