Group theory 1 st postulate combination of any

Group theory 1 st postulate - combination of any 2 elements, including element w/ itself, is a member of group. 2 nd postulate - set of elements of group contains identity element (IA = A) 3 rd postulate - for each element A, there is a unique element A' which is inverse of A (AA -1 = I) 1

Group theory Group multiplication tables - example: 2/m 1 Aπ m i 1 1 Aπ m i Aπ Aπ 1 i m m m i 1 Aπ i i m Aπ 1 2

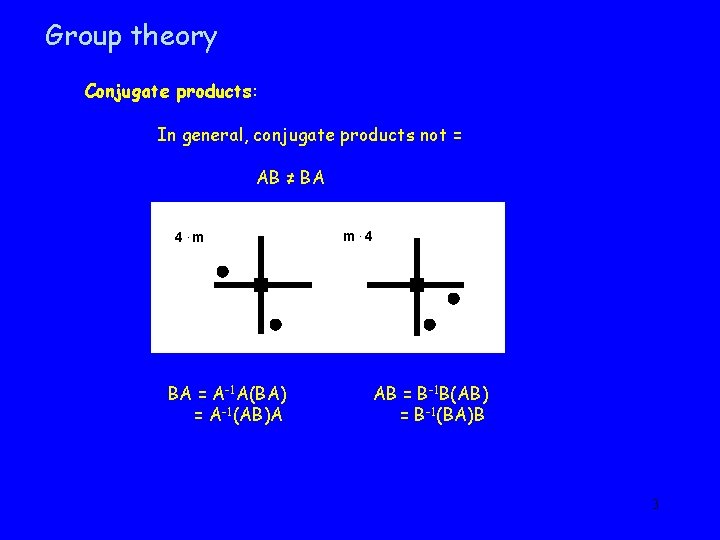
Group theory Conjugate products: In general, conjugate products not = AB ≠ BA 4. m BA = A-1 A(BA) = A-1(AB)A m. 4 AB = B-1 B(AB) = B-1(BA)B 3

Group theory Conjugate products: In general, conjugate products are not = AB ≠ BA BA = A-1 A(BA) = A-1(AB)A AB = B -1 B(AB) = B -1(BA)B Thm: transform of a product by its 1 st element is the conjugate product 4

Group theory Conjugate elements: If Y = A-1 XA then X & Y are conjugate elements 5

Group theory Conjugate elements: If Y = A-1 XA then X & Y are conjugate elements Sets of conjugate elements: Ex - in point group 322, 2 -fold axes 120° apart & 3 -fold axis these three 2 -fold axes form set of conjugate elements wrt 3 -fold axis 6

Group theory Invariant elements: If every element of group transforms a particular element of that group into itself, then that element is invariant Ex: 2 -fold axis in 2/m m, i, 1 take 2 into itself 7

Group theory Subgroups: Smaller collection of elements from group that is itself a group is a subgroup Ex: 2/m {1, Aπ, m, i} What are the subgroups? {1} {1, Aπ} {1, m} {1, i} {1, Aπ, m, i} 1 and the group itself are, formally, also subgroups 8

Group theory Subgroups: A smaller collection of elements from a group that is itself a group is a subgroup Notation: Group - G subgroup - g B is an "outside" element - in G, but not in g 9

Group theory Subgroups: A smaller collection of elements from a group that is itself a group is a subgroup Notation: Group - G subgroup - g B is an "outside" element - in G, but not in g Cosets: cosets g = a 1 a 2 …. g. B = a 1 B a 2 B …. a n. B Bg = Ba 1 Ba 2 …. Ban Elements of cosets must be in G an 10

Group theory Subgroups: Thm: the order of a subgroup is a factor of the order of the group. (order = # elements in g, or G) r elements of g: a 1 a 2 …. . ar B 2 …. . Bq are all outside elements 11

Group theory Subgroups: Thm: the order of a subgroup is a factor of the order of the group. (order = # elements in g, or G) r elements of g: a 1 a 2 …. . ar B 2 …. . Bq are all outside elements Then all elements of G are: g = a 1 a 2 …. . ar B 2 g = B 2 a 1 B 2 a 2 …. . B 2 ar B 3 g = B 3 a 1 B 3 a 2 …. . B 3 ar Bqg = Bqa 1 Bqa 2 …. . Bqar 12

Group theory Subgroups: Thm: the order of a subgroup is a factor of the order of the group. (order = # elements in g, or G) Then all elements of G are: g = a 1 a 2 …. . ar B 2 g = B 2 a 1 B 2 a 2 …. . B 2 ar B 3 g = B 3 a 1 B 3 a 2 …. . B 3 ar Bqg = Bqa 1 Bqa 2 …. . Bqar qr elements in G q = index of subgroup g 13

Group theory Subgroups: Ex: g = 1, i (order 2) G = 1, Aπ, m, i (order 4) B 2 = Aπ B 3 = m 14

Group theory Subgroups: Ex: g = 1, i (order 2) G = 1, Aπ, m, i (order 4) B 2 = Aπ B 3 = m g = 1 i B 2 g = Aπ Aπ i = Aπ B 3 g = m m i = m m Aπ Since B 2 g = B 3 g, g is of index 2 only 15

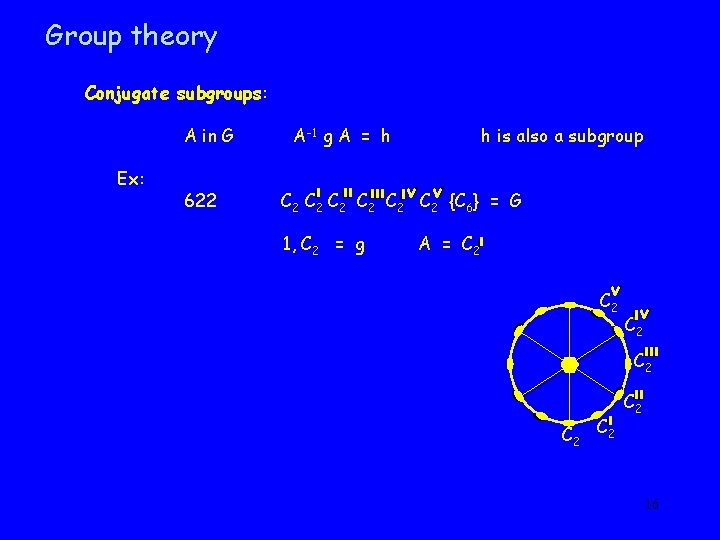
Group theory Conjugate subgroups: A in G Ex: 622 A-1 g A = h h is also a subgroup C 2 C 2 C 2 {C 6} = G 1, C 2 = g A = C 2 C 2 16

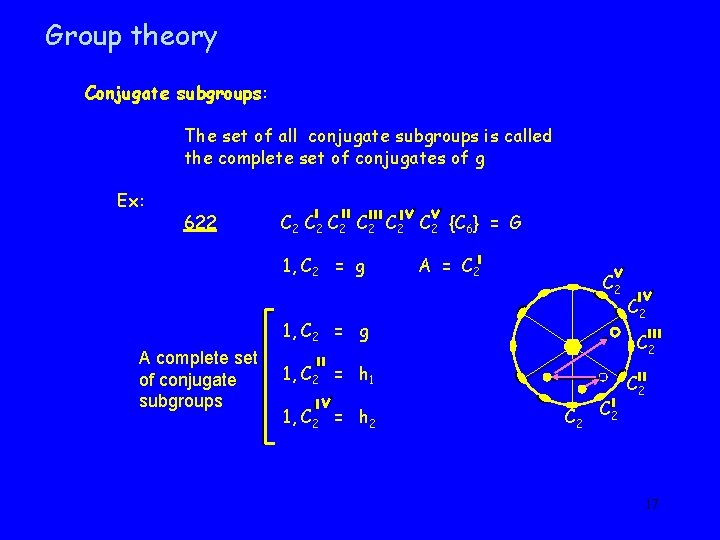
Group theory Conjugate subgroups: The set of all conjugate subgroups is called the complete set of conjugates of g Ex: 622 C 2 C 2 C 2 {C 6} = G 1, C 2 = g A = C 2 1, C 2 = g A complete set of conjugate subgroups C 2 1, C 2 = h 1 1, C 2 = h 2 C 2 C 2 17

Group theory Invariant subgroups: An invariant subgroup is self conjugate For every B in G B-1 g. B = g g. B = Bg (right & left cosets =) g. B = a 1 B ……. . an. B Bg = Ba 1 ……. . Ban 2 collections of same set of elements 18

Group theory Invariant subgroups: Ex: 2/m G = 1, C 2, m, i g = 1, C 2 19

Group theory Invariant subgroups: Ex: 2/m G = 1, C 2, m, i g = 1, C 2 1 1 1=1 1 C 2 1 = C 2 m-1 C 2 m = C 2 i-1 C 2 i = C 2 20

Group theory Invariant subgroups: Every subgroup of index two is invariant G = g, g. B G = g, Bg 21

Group theory Invariant subgroups: Every subgroup of index two is invariant G = g, g. B G = g, Bg Ex: 2/m G = 1, C 2, m, i g = 1, C 2 B=m G = 1, C 2, 1 m, C 2 m = 1, C 2, m, i G = 1, C 2, m 1, m C 2 = 1, C 2, m, i 1 m=m 1 m C 2 = C 2 m 22

Group theory Group products: Suppose group g (= a 1 …. ar) B not in g Thm: if element B of order 2 transforms group g into itself then elements in g and Bg form a group g = a 1 …. ar Bg = Ba 1 …. Bar and Bg = g. B (g is of index 2) 23

Group theory Group products: Suppose group g (= a 1 …. ar) B not in g Thm: if element B of order 2 transforms group g into itself then elements in g and Bg form a group g = a 1 …. ar Bg = Ba 1 …. Bar and Bg = g. B (g is of order 2) Since g is a group, ai aj = ak; ak in g Then Bai aj = Bak; Products for are Bak in Bg Bai Baj ai = Bai B-1 ai B = B a i 24

Group theory Group products: Since g is a group, ai aj = ak; ak in g Then Bai aj = Bak; Products for Bg are Bak in Bg Bai Baj ai = Bai B-1 ai B = B a i Baj = ai B Baj BB =I since B is of order 2 Bai Baj = ai aj Since B transforms g into itself, ai’ is an element in g Thus Bai Baj with ai aj form a closed set 25

Group theory Group products: Identity is in g Inverses - an-1 in g -1 -1 -1 (Ban)-1 = an B-1 = B-1 (an ) = B (an ) Therefore in Bg g, Bg is a group 26

Group theory Group products: Extended arguments give Thm: if g & h two groups w/ no common element except I & if each element of h transforms g into itself then the set of products of g & h form a group 27