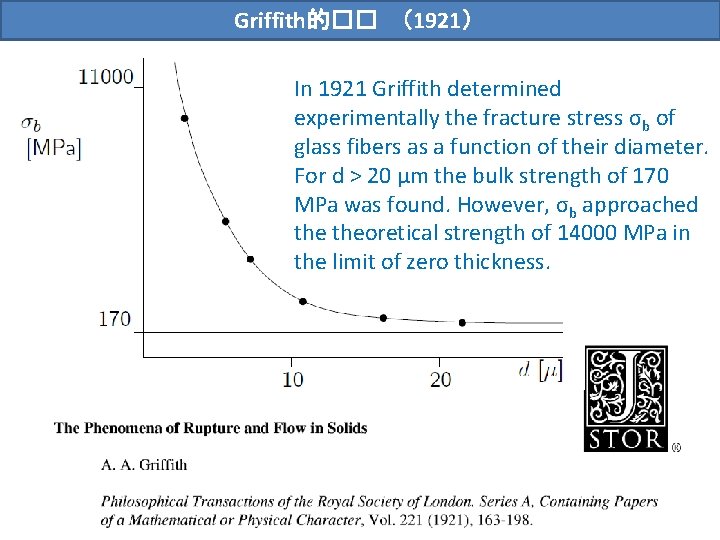
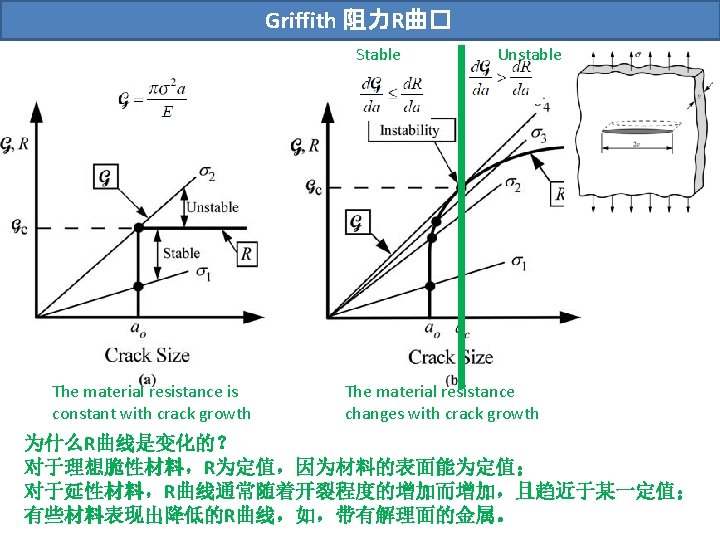
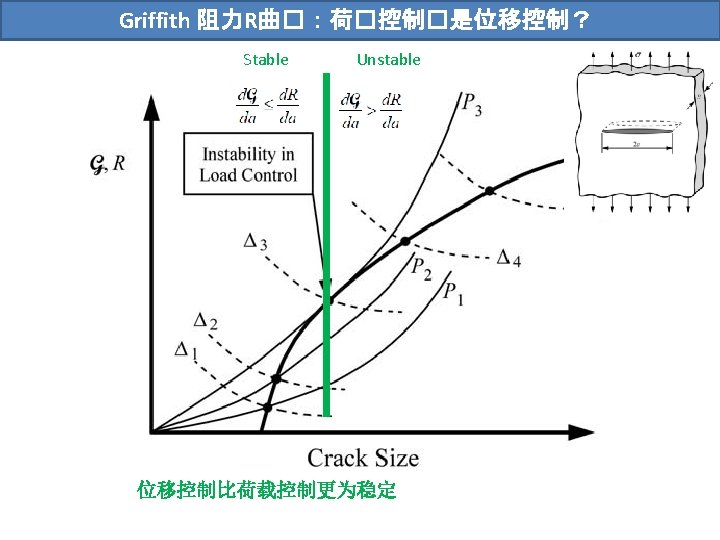
Griffith 1921 In 1921 Griffith determined experimentally the

Griffith的�� （1921） In 1921 Griffith determined experimentally the fracture stress σb of glass fibers as a function of their diameter. For d > 20 μm the bulk strength of 170 MPa was found. However, σb approached theoretical strength of 14000 MPa in the limit of zero thickness.

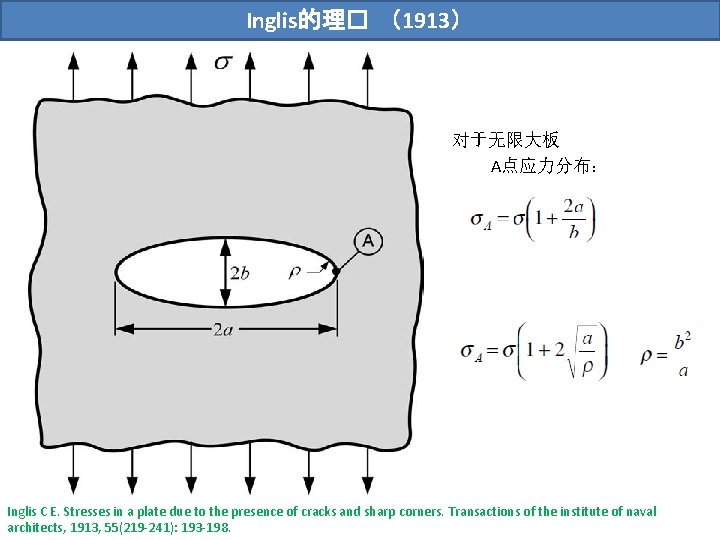
Inglis的理� （1913） 对于无限大板 A点应力分布： Inglis C E. Stresses in a plate due to the presence of cracks and sharp corners. Transactions of the institute of naval architects, 1913, 55(219 -241): 193 -198.

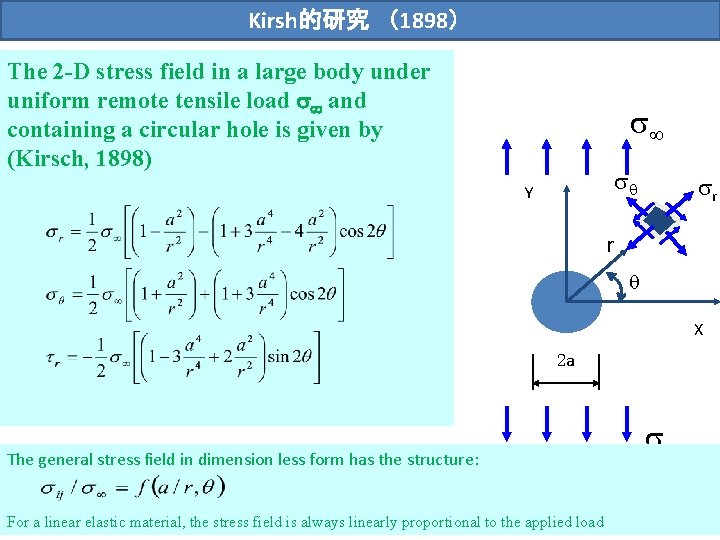
Kirsh的研究 （1898） The 2 -D stress field in a large body under uniform remote tensile load and containing a circular hole is given by (Kirsch, 1898) Y r r X 2 a The general stress field in dimension less form has the structure: For a linear elastic material, the stress field is always linearly proportional to the applied load

Kirsh的研究 （1898） 理�推�：一般情况 平面极坐标下的应力分量： 双调和函数： Kirsch E G. Die Theorie der Elastizit t und die Bed rfnisse der Festigkeitslehre. Zeitshrift des Vereines deutscher Ingenieure, 1898, 42: 797 -807.

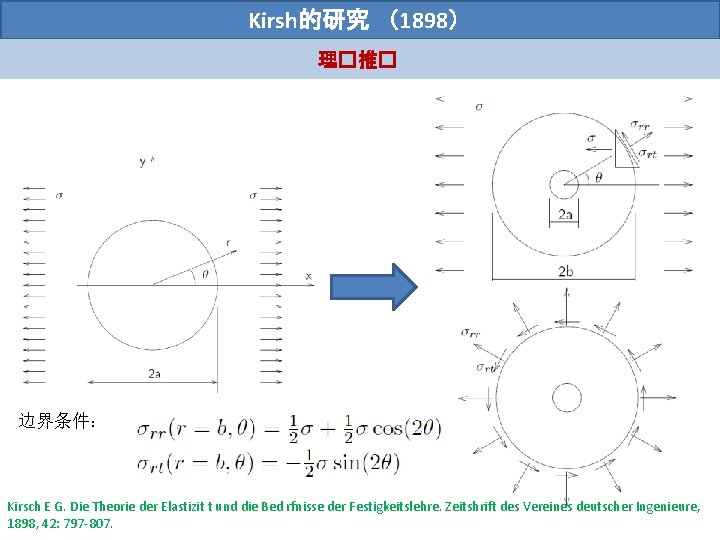
Kirsh的研究 （1898） 理�推� 边界条件： Kirsch E G. Die Theorie der Elastizit t und die Bed rfnisse der Festigkeitslehre. Zeitshrift des Vereines deutscher Ingenieure, 1898, 42: 797 -807.

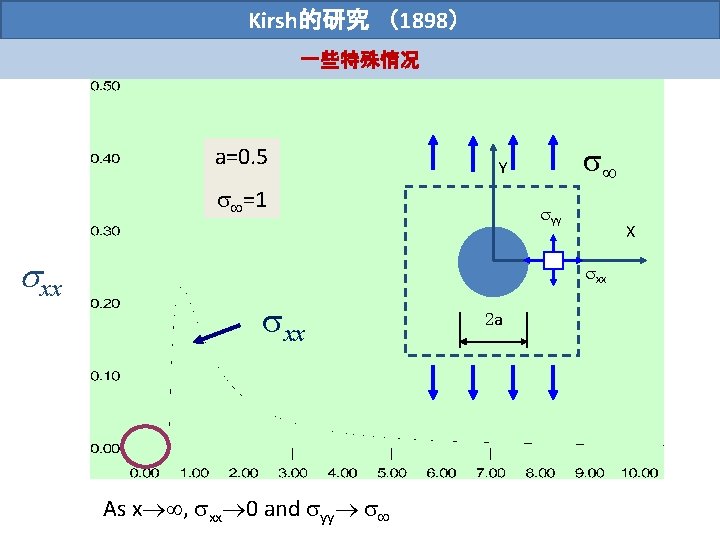
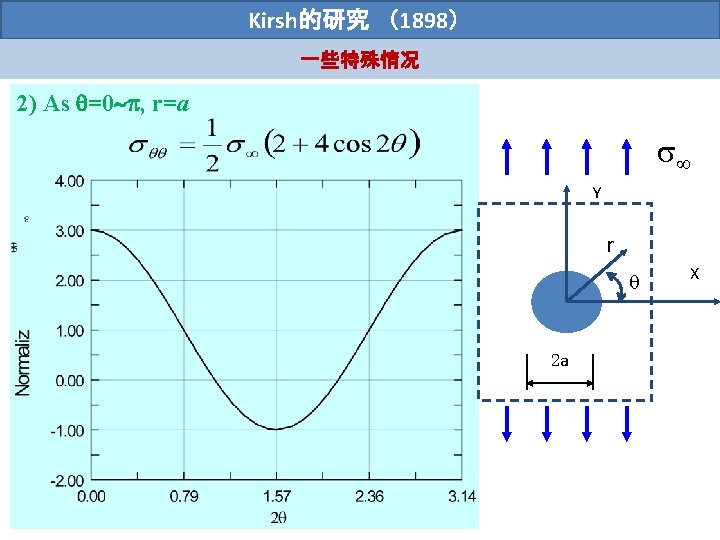
Kirsh的研究 （1898） 一些特殊情况 Several aspects of this stress field are worth our attention: 1) As =0 Y yy X xx 2 a As x , xx 0 and yy

Kirsh的研究 （1898） 一些特殊情况 a=0. 5 =1 xx Y yy X xx As x , xx 0 and yy 2 a

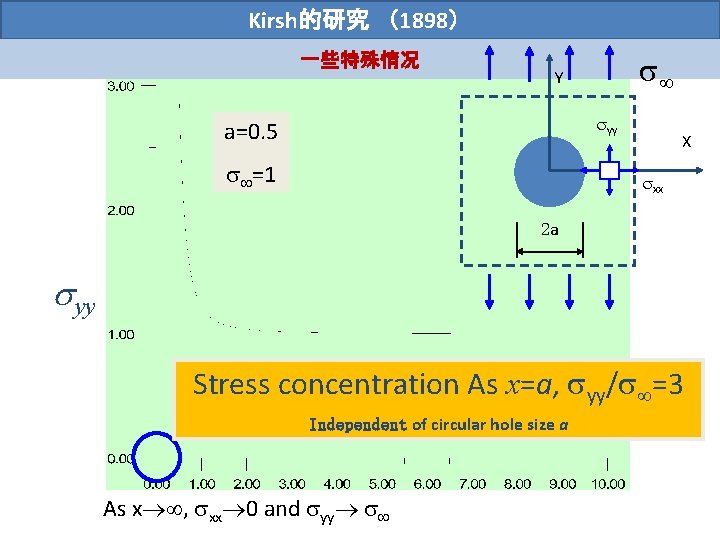
Kirsh的研究 （1898） 一些特殊情况 Y yy a=0. 5 =1 X xx 2 a yy Stress concentration As x=a, yy/ =3 Independent of circular hole size a As x , xx 0 and yy

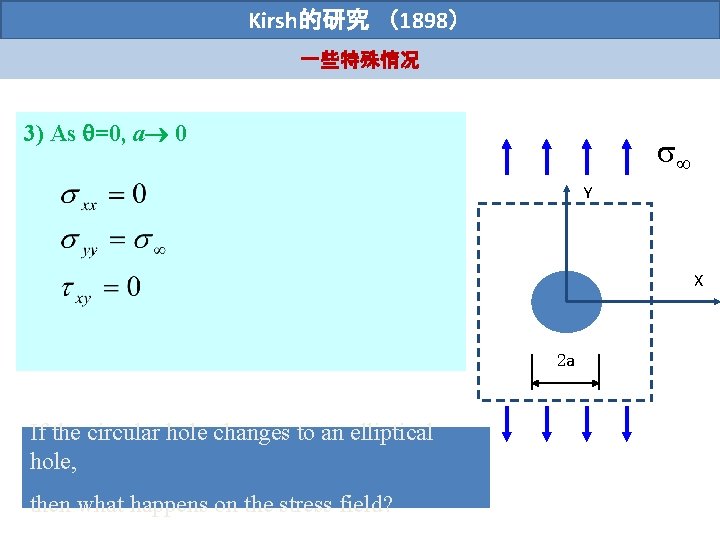
Kirsh的研究 （1898） 一些特殊情况 3) As =0, a 0 Y X 2 a If the circular hole changes to an elliptical hole, then what happens on the stress field?

��形孔洞： Inglis的理� （1913） The 2 -D elastic solution for a large body containing an elliptical cavity under uniform remote tensile load was given by (Inglis, 1913) 2 b ym yy xm xx X 2 a Further discussion: 1)When a=b, then the stress concentration factor of three is recovered for a circular defect; 2) When 0 (the ellipse flattens and become a crack-like defect, ym , no material can withstand infinite stress, so material at ellipse tip must become inelastic, plastic yielding or other inelastic processes

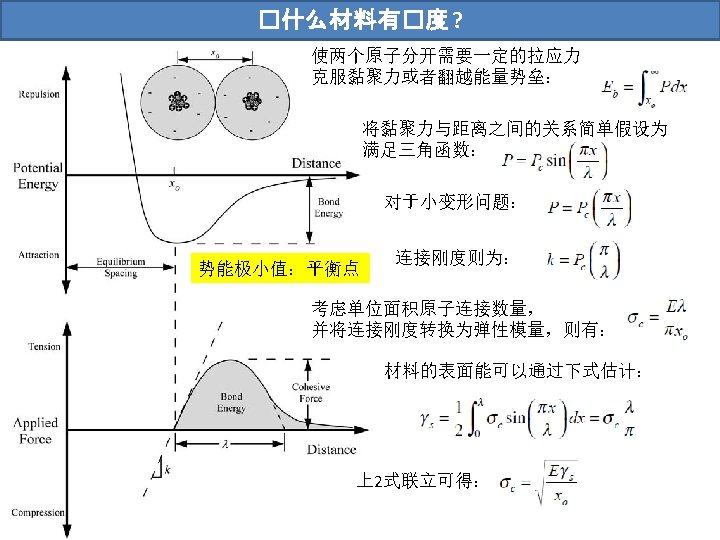
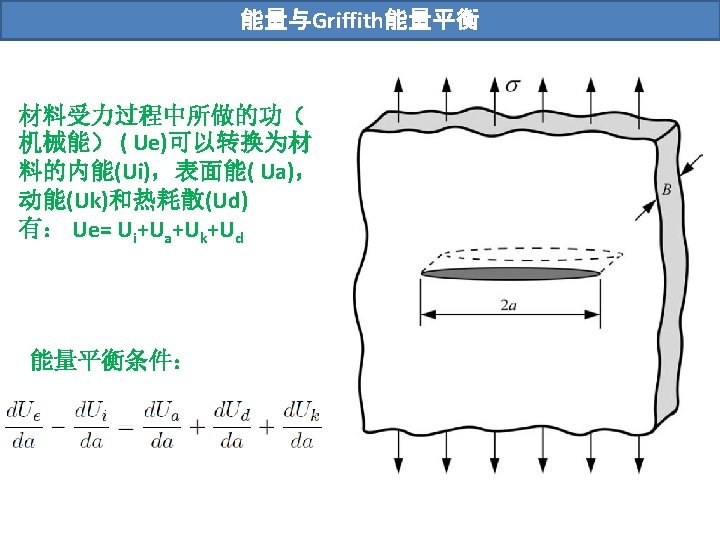
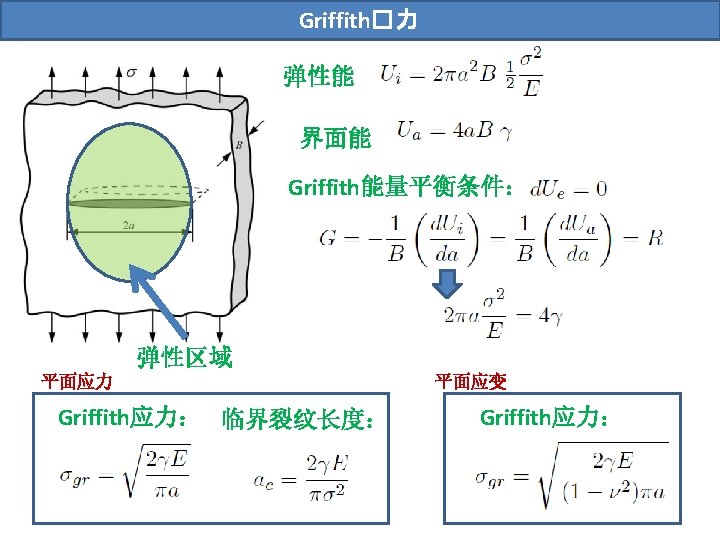
能量与Griffith能量平衡 “It may be supposed, for the present purpose, that the crack is formed by the sudden annihilation of the tractions acting on its surface. At the instant following this operation, the strains, and therefore the potential energy under consideration, have their original values; but in general, the new state is not one of equilibrium. If it is not a state of equilibrium, then, by theorem of minimum potential energy, the potential energy is reduced by the attainment of equilibrium; if it is a state of equilibrium, the energy does not change. ” 现假设材料的动能(Uk)和热耗散(Ud)均可忽略不计，那么单位 长度裂纹扩展所需的能量即为新形成表面所需的能量： 并有以下定义

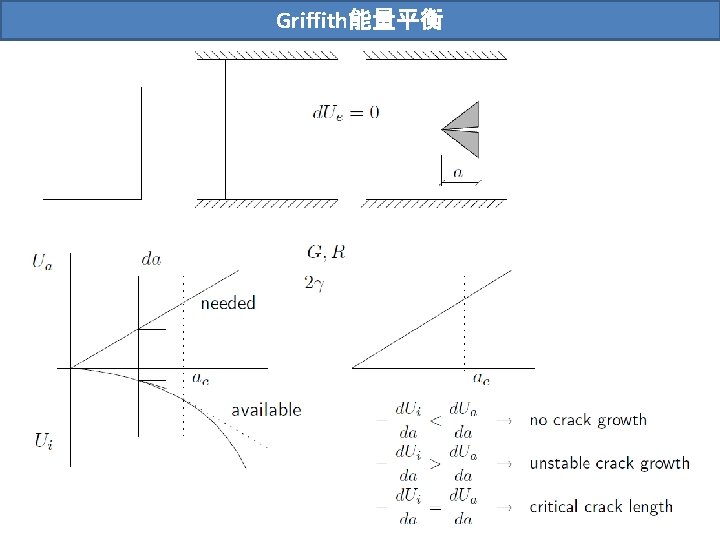
Griffith能量平衡

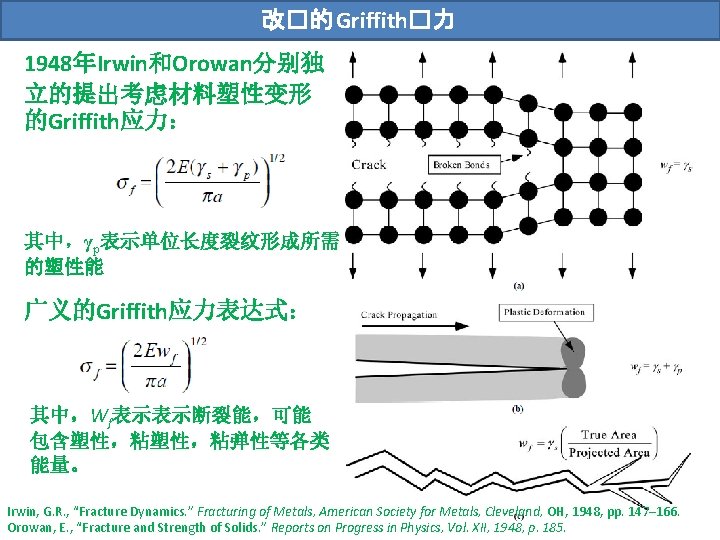
改�的 Griffith�力 1948年Irwin和Orowan分别独 立的提出考虑材料塑性变形 的Griffith应力： 其中，γp表示单位长度裂纹形成所需 的塑性能 广义的Griffith应力表达式： 其中，Wf表示表示断裂能，可能 包含塑性，粘弹性等各类 能量。 Irwin, G. R. , “Fracture Dynamics. ” Fracturing of Metals, American Society for Metals, Cleveland, OH, 1948, pp. 147– 166. Orowan, E. , “Fracture and Strength of Solids. ” Reports on Progress in Physics, Vol. XII, 1948, p. 185.

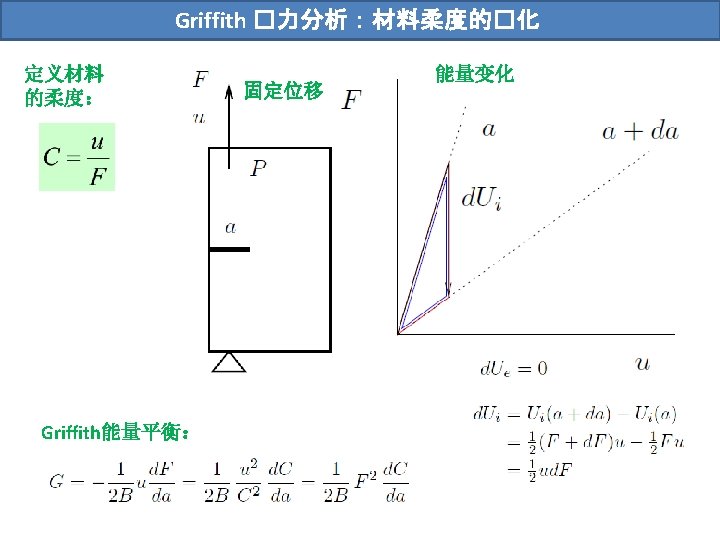
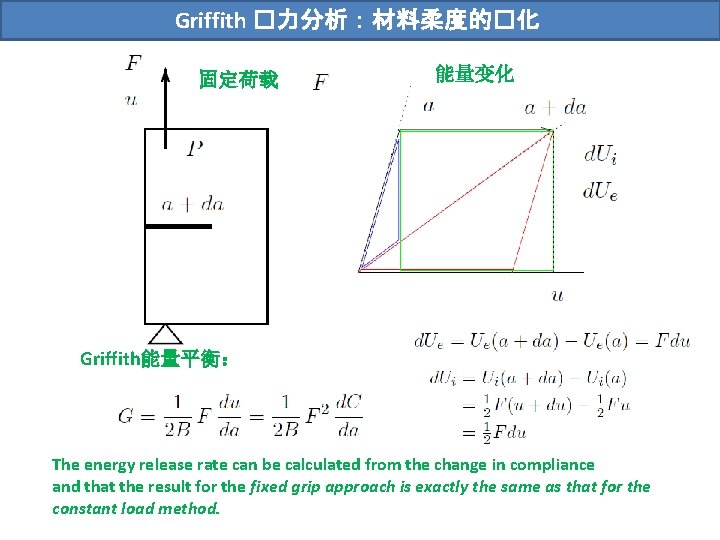
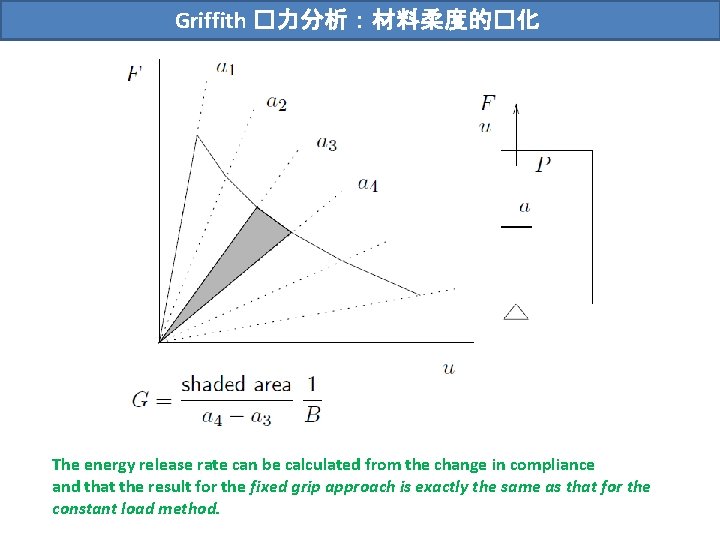
Griffith �力分析：材料柔度的�化 固定荷载 能量变化 Griffith能量平衡： The energy release rate can be calculated from the change in compliance and that the result for the fixed grip approach is exactly the same as that for the constant load method.

Griffith �力分析：材料柔度的�化 The energy release rate can be calculated from the change in compliance and that the result for the fixed grip approach is exactly the same as that for the constant load method.

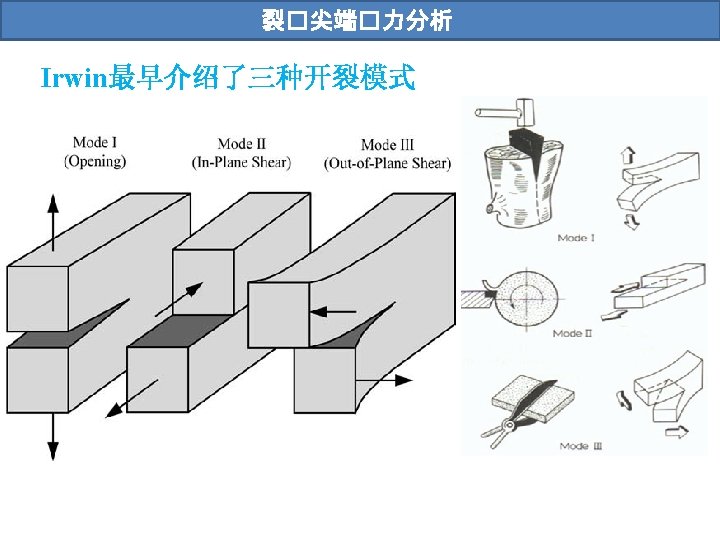
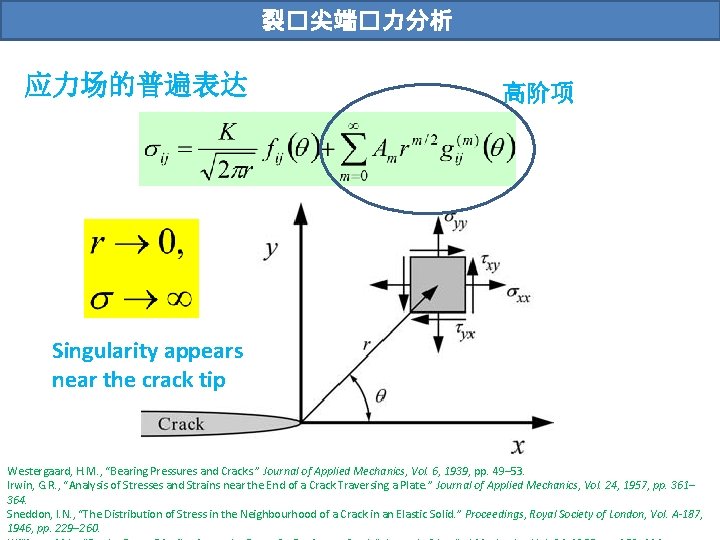
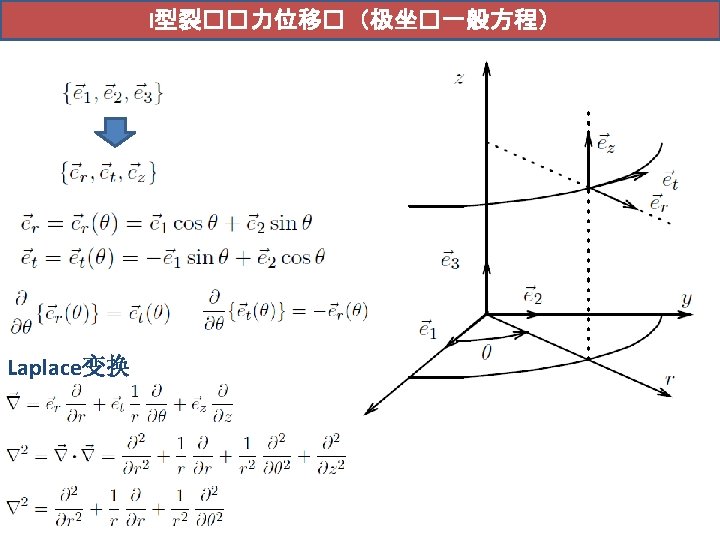
裂�尖端�力分析 应力场的普遍表达 高阶项 Singularity appears near the crack tip Westergaard, H. M. , “Bearing Pressures and Cracks. ” Journal of Applied Mechanics, Vol. 6, 1939, pp. 49– 53. Irwin, G. R. , “Analysis of Stresses and Strains near the End of a Crack Traversing a Plate. ” Journal of Applied Mechanics, Vol. 24, 1957, pp. 361– 364. Sneddon, I. N. , “The Distribution of Stress in the Neighbourhood of a Crack in an Elastic Solid. ” Proceedings, Royal Society of London, Vol. A-187, 1946, pp. 229– 260.

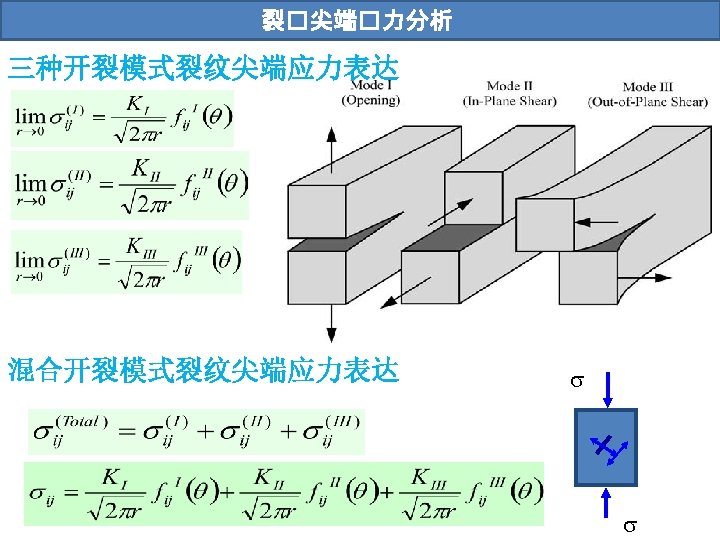
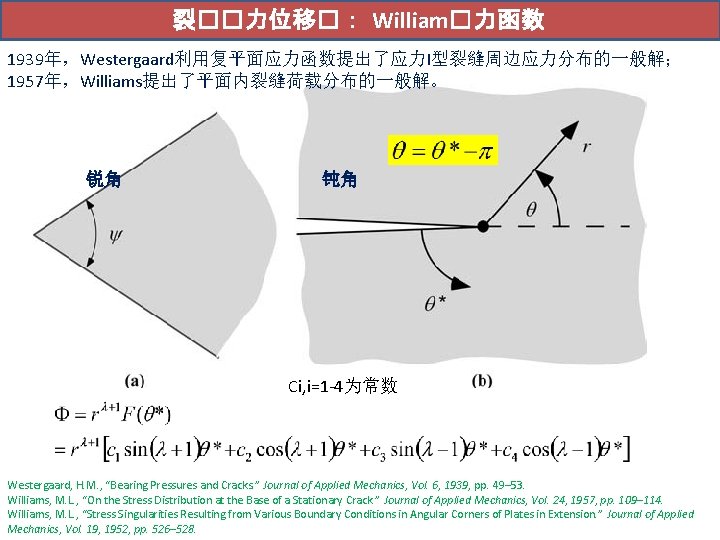
裂��力位移�： William�力函数 1939年，Westergaard利用复平面应力函数提出了应力I型裂缝周边应力分布的一般解； 1957年，Williams提出了平面内裂缝荷载分布的一般解。 锐角 钝角 Ci, i=1 -4为常数 Westergaard, H. M. , “Bearing Pressures and Cracks. ” Journal of Applied Mechanics, Vol. 6, 1939, pp. 49– 53. Williams, M. L. , “On the Stress Distribution at the Base of a Stationary Crack. ” Journal of Applied Mechanics, Vol. 24, 1957, pp. 109– 114. Williams, M. L. , “Stress Singularities Resulting from Various Boundary Conditions in Angular Corners of Plates in Extension. ” Journal of Applied Mechanics, Vol. 19, 1952, pp. 526– 528.

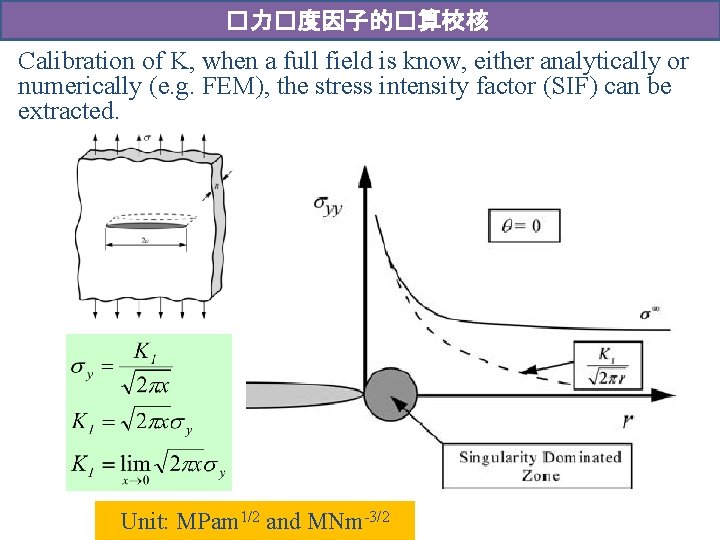
�力�度因子的�算校核 Calibration of K, when a full field is know, either analytically or numerically (e. g. FEM), the stress intensity factor (SIF) can be extracted. Unit: MPam 1/2 and MNm-3/2

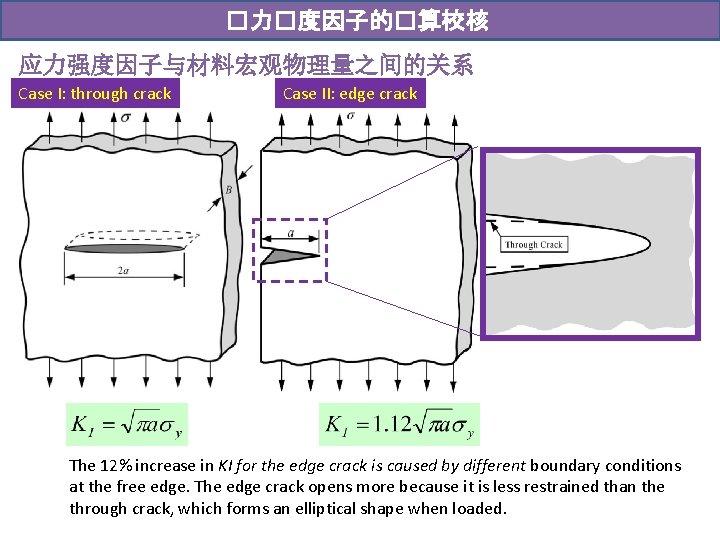
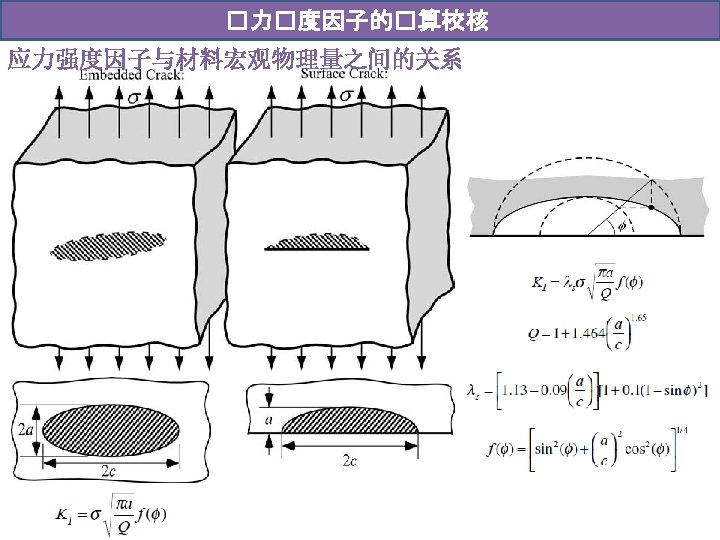
�力�度因子的�算校核 应力强度因子与材料宏观物理量之间的关系 Case I: through crack Case II: edge crack The 12% increase in KI for the edge crack is caused by different boundary conditions at the free edge. The edge crack opens more because it is less restrained than the through crack, which forms an elliptical shape when loaded.

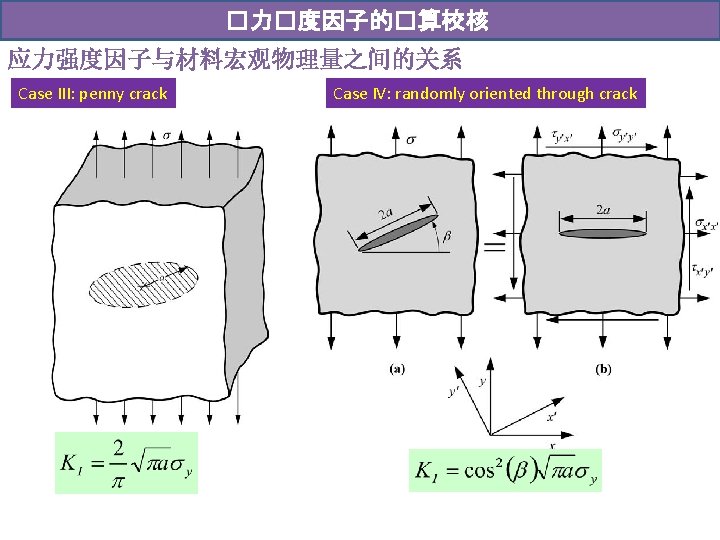
�力�度因子的�算校核 应力强度因子与材料宏观物理量之间的关系 Case III: penny crack Case IV: randomly oriented through crack

�力�度因子的�算校核 应力强度因子计算实例 已知：材料尺寸和荷载情况见右图， y=0 处的应力场可以表示为 问题： (1) Derive the stress intensity factor (KI) for the given configuration using the above stress field. (2) Give the crack tip approximate stress field ( yy) using above stress intensity factor (KI). (3) Assume the acceptable tolerance in the stress field yy is 10%, i. e. solve the outer limit of the zone (K- dominant zone) in the form of x/a.

�力�度因子的�算校核 解： (1)Shift the co-ordinate to the crack tip, then: x’=x-a and x=x’+a (2) (3) Approximate solution of yy Exact solution of yy

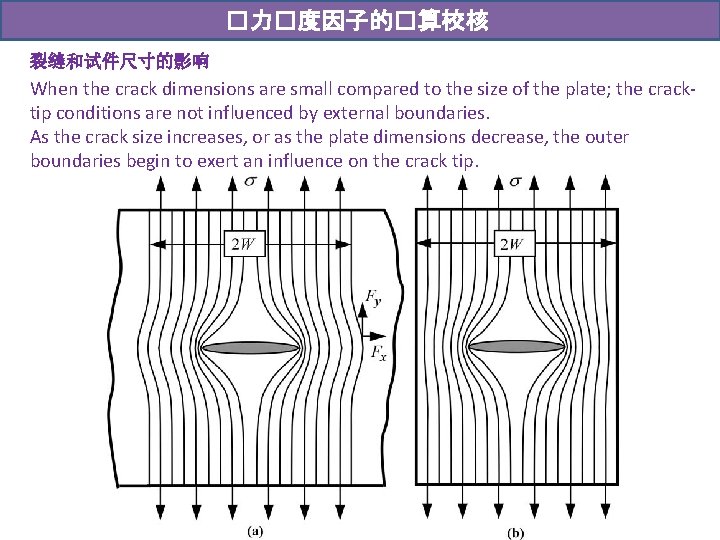
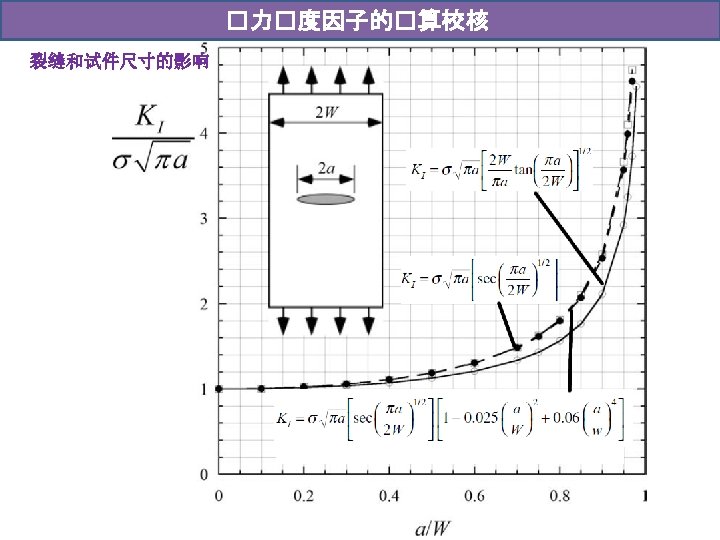
�力�度因子的�算校核 裂缝和试件尺寸的影响 When the crack dimensions are small compared to the size of the plate; the cracktip conditions are not influenced by external boundaries. As the crack size increases, or as the plate dimensions decrease, the outer boundaries begin to exert an influence on the crack tip.

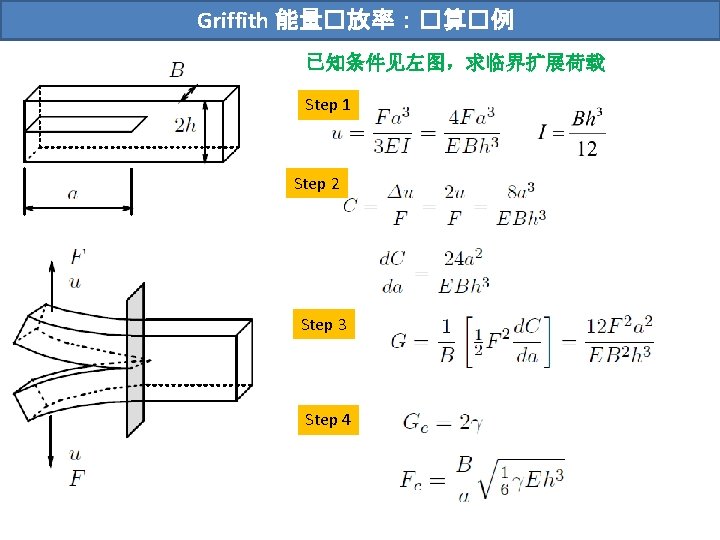
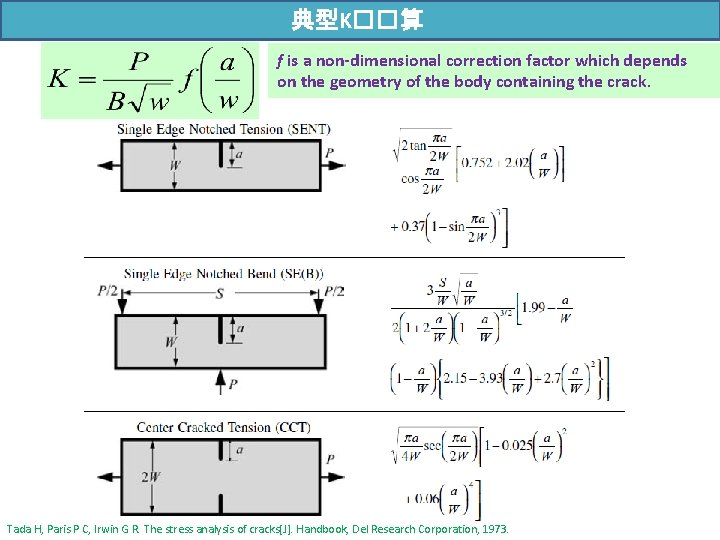
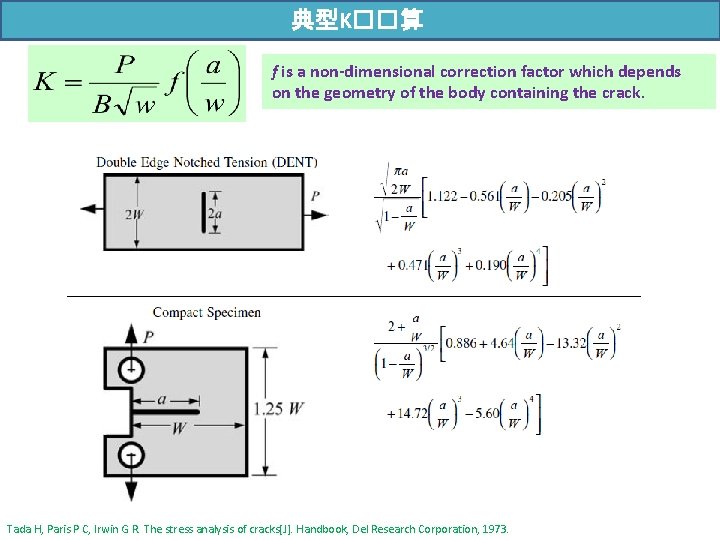
典型K��算 f is a non-dimensional correction factor which depends on the geometry of the body containing the crack. Tada H, Paris P C, Irwin G R. The stress analysis of cracks[J]. Handbook, Del Research Corporation, 1973.

典型K��算 f is a non-dimensional correction factor which depends on the geometry of the body containing the crack. Tada H, Paris P C, Irwin G R. The stress analysis of cracks[J]. Handbook, Del Research Corporation, 1973.

典型K��算 Tada H, Paris P C, Irwin G R. The stress analysis of cracks[J]. Handbook, Del Research Corporation, 1973.

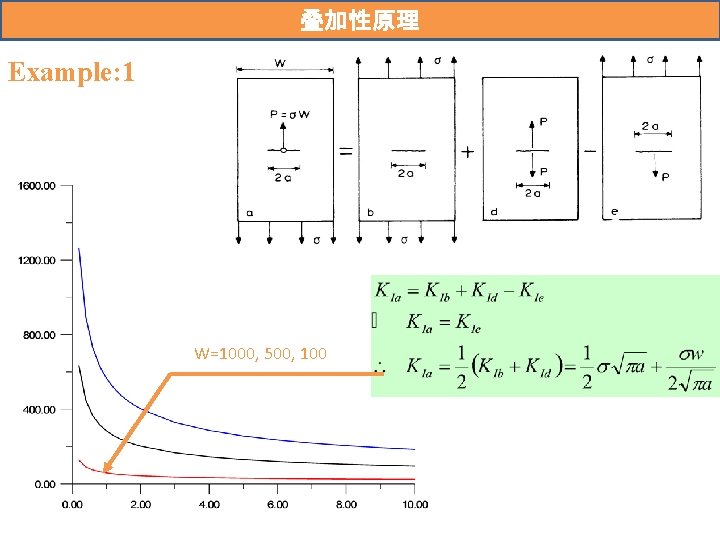
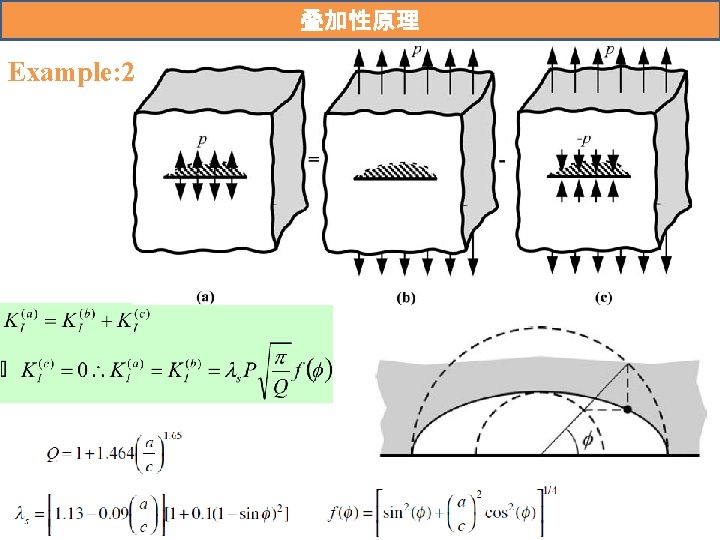
叠加性原理 For linear elastic materials, individual components of stress, strain, and displacement are additive. The stress intensity factor for a combination of load systems p, q, r. . . can be obtained simply by superposition: But

叠加性原理 Example: 1 W=1000, 500, 100

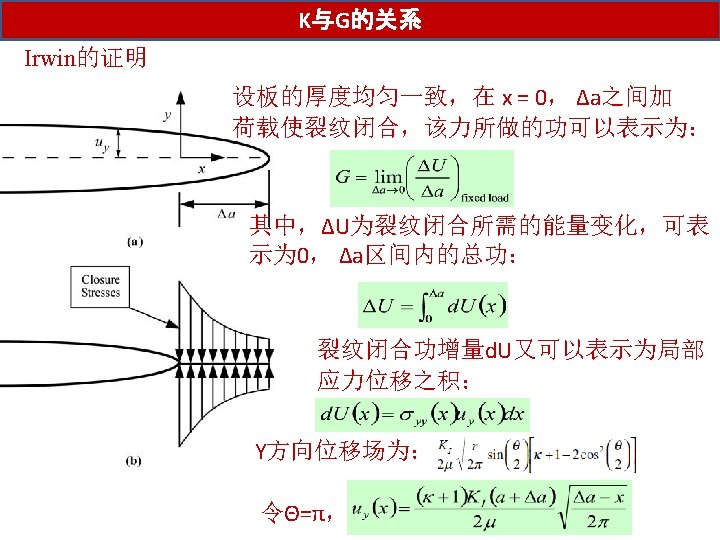
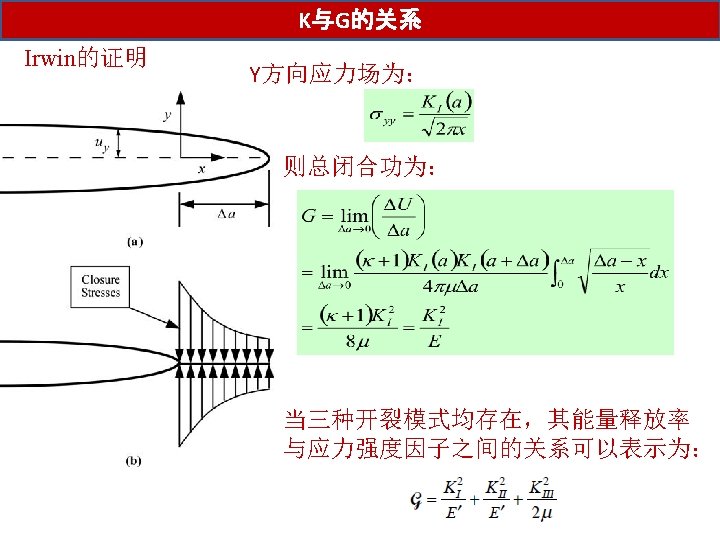
K与G的关系 We now know tow important parameters: the energy release rate G and the stress intensity factor K, The energy release rate describes global behavior, while K is a local parameter Is one related to the other? For linear elastic materials, YES Plane stress Plane strain G-K relations apply only to a through crack in an infinite plate, are they the general relationships that apply to all configurations?

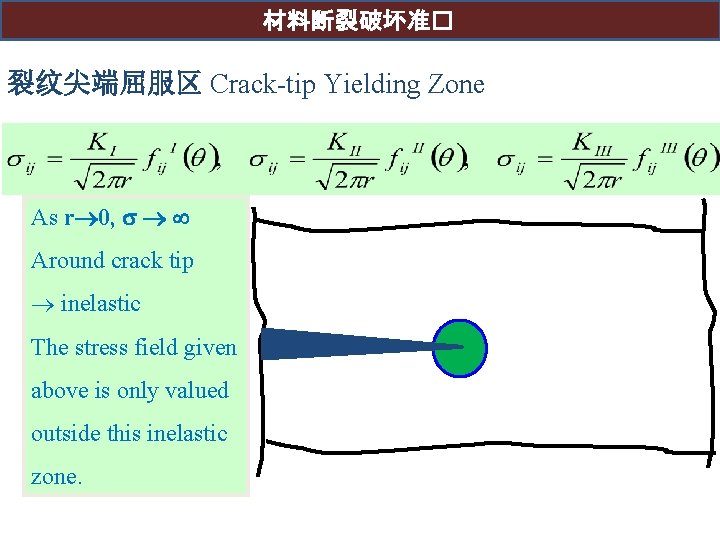
材料断裂破坏准� 裂纹尖端屈服区 Crack-tip Yielding Zone As r 0, Around crack tip inelastic The stress field given above is only valued outside this inelastic zone.

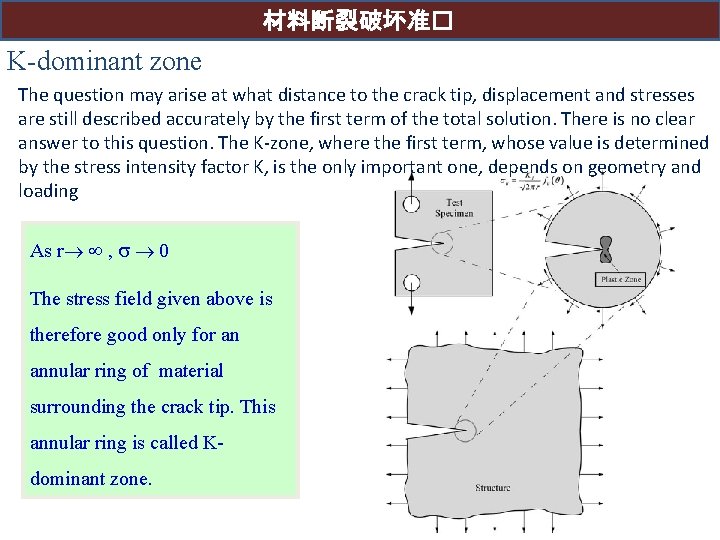
材料断裂破坏准� K-dominant zone The question may arise at what distance to the crack tip, displacement and stresses are still described accurately by the first term of the total solution. There is no clear answer to this question. The K-zone, where the first term, whose value is determined by the stress intensity factor K, is the only important one, depends on geometry and loading As r , 0 The stress field given above is therefore good only for an annular ring of material surrounding the crack tip. This annular ring is called Kdominant zone.

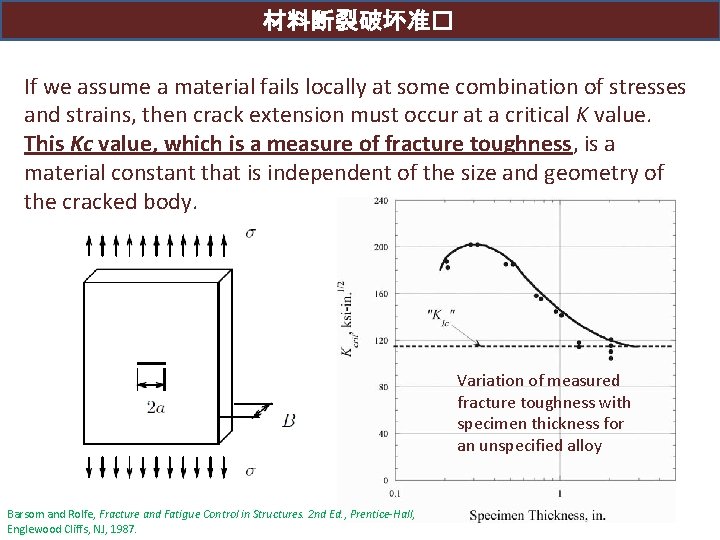
材料断裂破坏准� If we assume a material fails locally at some combination of stresses and strains, then crack extension must occur at a critical K value. This Kc value, which is a measure of fracture toughness, is a material constant that is independent of the size and geometry of the cracked body. Variation of measured fracture toughness with specimen thickness for an unspecified alloy Barsom and Rolfe, Fracture and Fatigue Control in Structures. 2 nd Ed. , Prentice-Hall, Englewood Cliffs, NJ, 1987.

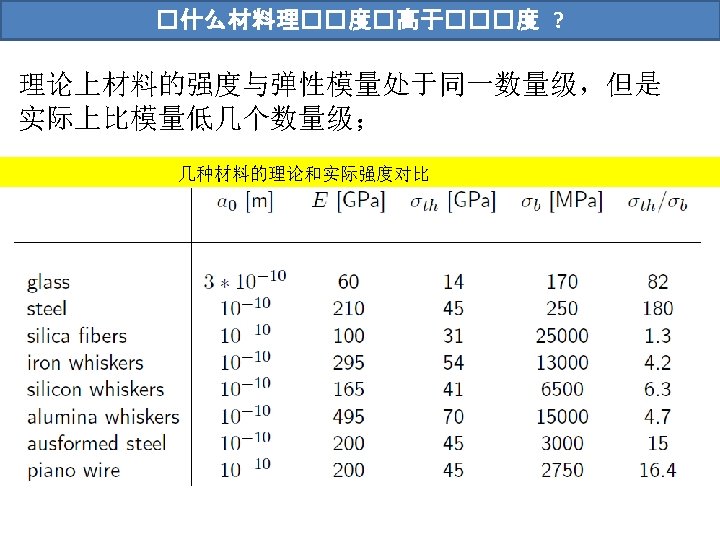
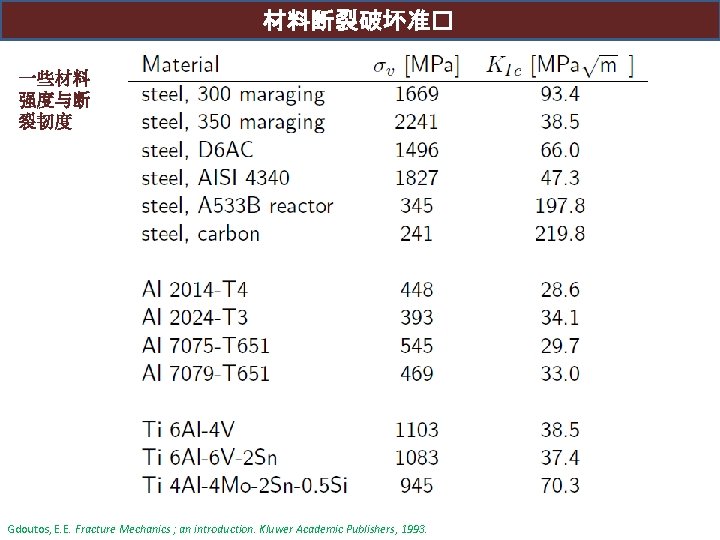
材料断裂破坏准� 一些材料 强度与断 裂韧度 Gdoutos, E. E. Fracture Mechanics ; an introduction. Kluwer Academic Publishers, 1993.

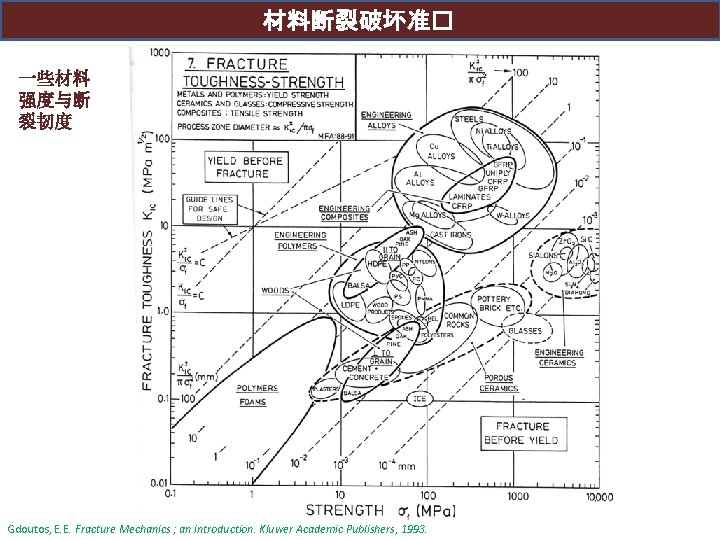
材料断裂破坏准� 一些材料 强度与断 裂韧度 Gdoutos, E. E. Fracture Mechanics ; an introduction. Kluwer Academic Publishers, 1993.

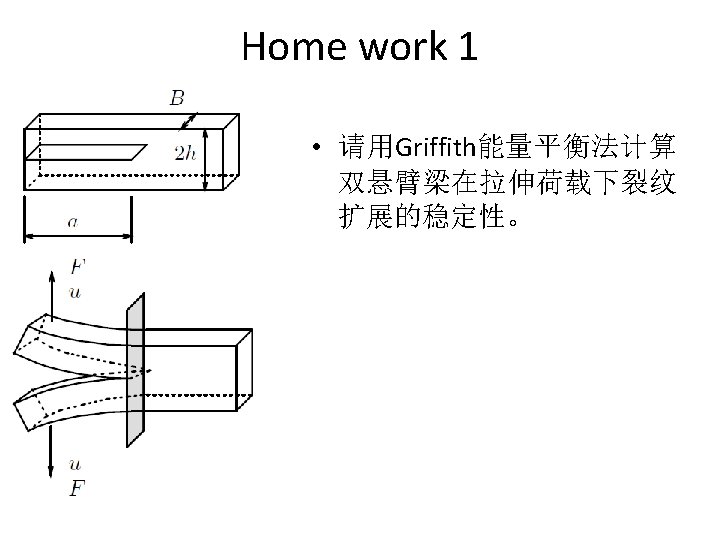
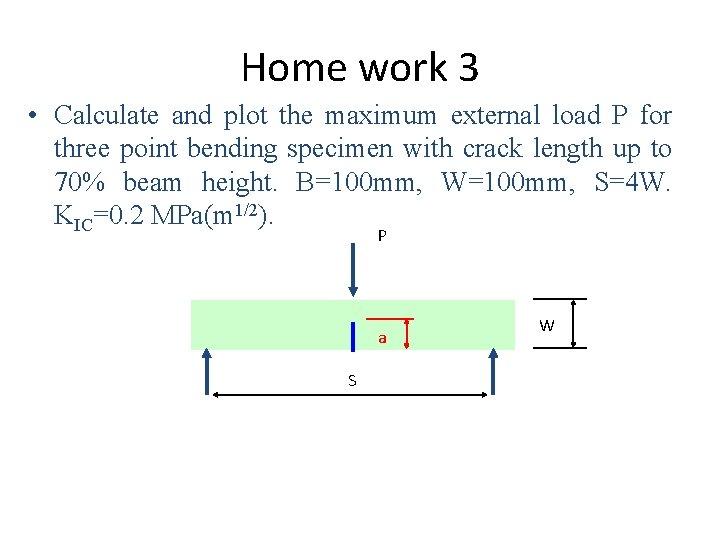
Home work 3 • Calculate and plot the maximum external load P for three point bending specimen with crack length up to 70% beam height. B=100 mm, W=100 mm, S=4 W. KIC=0. 2 MPa(m 1/2). P a S W