Greedy Algorithms Neil Tang 4292008 CS 223 Advanced

Greedy Algorithms Neil Tang 4/29/2008 CS 223 Advanced Data Structures and Algorithms 1

Course Survey Please complete the course survey by May 3 (Sat) at: http: //www. cs. montana. edu/survey/ CS 223 Advanced Data Structures and Algorithms 2

Class Overview Ø Basic idea Ø Examples: Greedy is good Ø The bin packing problem Ø The online algorithms Ø The offline algorithms CS 223 Advanced Data Structures and Algorithms 3

Basic Idea Ø In each phase, it makes the best choice based on the current partial solution and the performance metric. Ø No future consequences are considered when making decisions. Ø Usually it will not go back to change the previous choices. CS 223 Advanced Data Structures and Algorithms 4

Examples: Greedy is good Ø Dijkstra’s algorithm Ø Prim’s algorithm Ø Kruskal’s algorithm CS 223 Advanced Data Structures and Algorithms 5

Bin Packing Ø Bin packing: Given N items with sizes s 1, s 2, …, s. N, where 0 si 1. The bin packing is to pack these items in the fewest bins, given that each bin has unit capacity. Ø Online bin packing (dynamic case): Each item must be placed in a bin before the size of the next item is given. Ø Offline bin packing (static case): You can make decision until all the input has been read. CS 223 Advanced Data Structures and Algorithms 6

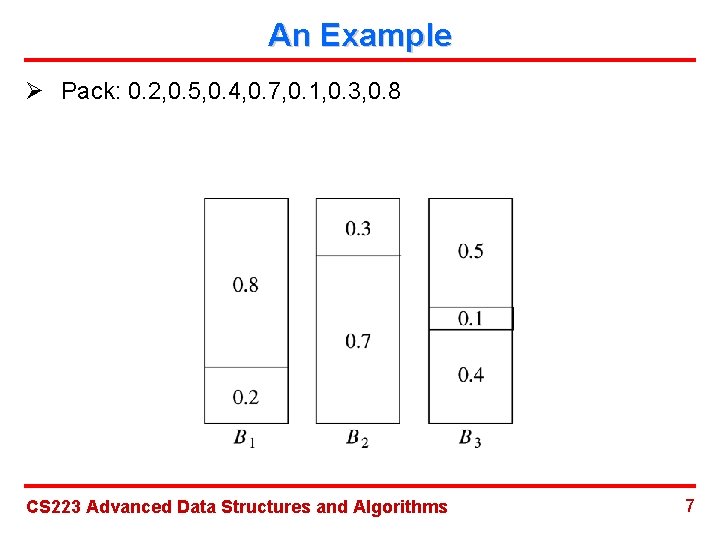
An Example Ø Pack: 0. 2, 0. 5, 0. 4, 0. 7, 0. 1, 0. 3, 0. 8 CS 223 Advanced Data Structures and Algorithms 7

The Next Fit Algorithm Ø For each new item, check to see if it fits in the same bin as the last one. If it does, place it there. Otherwise, create a new bin. Ø Time complexity: O(N). CS 223 Advanced Data Structures and Algorithms 8

The Next Fit Algorithm Ø Pack: 0. 2, 0. 5, 0. 4, 0. 7, 0. 1, 0. 3, 0. 8 CS 223 Advanced Data Structures and Algorithms 9

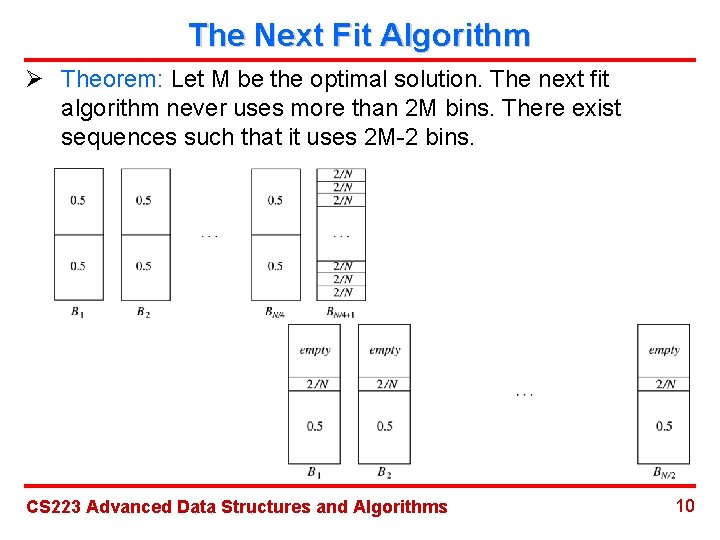
The Next Fit Algorithm Ø Theorem: Let M be the optimal solution. The next fit algorithm never uses more than 2 M bins. There exist sequences such that it uses 2 M-2 bins. CS 223 Advanced Data Structures and Algorithms 10

The First Fit Algorithm Ø For each new item, scan the existing bins in order and place it in the first bin that can hold it. Create a new bin if none of them can hold it. Ø Time complexity: O(N 2) CS 223 Advanced Data Structures and Algorithms 11

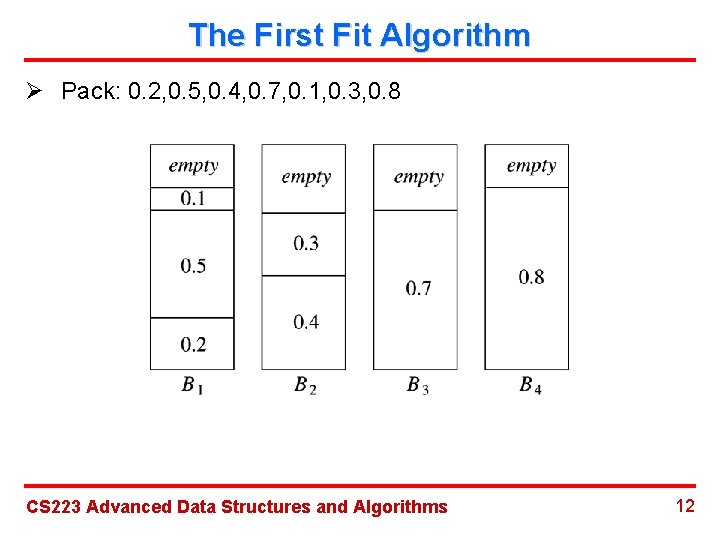
The First Fit Algorithm Ø Pack: 0. 2, 0. 5, 0. 4, 0. 7, 0. 1, 0. 3, 0. 8 CS 223 Advanced Data Structures and Algorithms 12

The First Fit Algorithm Ø Theorem: Let M be the optimal solution. The first fit algorithm never uses more than 1. 7 M bins. There exist sequences such that it uses 1. 7(M-1) bins. CS 223 Advanced Data Structures and Algorithms 13

The Best Fit Algorithm Ø For each new item, scan the existing bins in order and place it in the tightest spot among all bins. Create a new bin if none of them can hold it. Ø Time complexity: O(N 2) CS 223 Advanced Data Structures and Algorithms 14

The Best Fit Algorithm Ø Pack: 0. 2, 0. 5, 0. 4, 0. 7, 0. 1, 0. 3, 0. 8 CS 223 Advanced Data Structures and Algorithms 15

The Offline Algorithms Ø The first/best fit decreasing algorithm: Sort the sizes in the descending order, then use the first/best fit algorithm. Ø Time complexity: O(N 2) CS 223 Advanced Data Structures and Algorithms 16

The Offline Algorithms Ø First fit for 0. 8, 0. 7, 0. 5, 0. 4, 0. 3, 0. 2, 0. 1 CS 223 Advanced Data Structures and Algorithms 17

The Offline Algorithms Ø Theorem: Let M be the optimal solution. The first fit descending algorithm never uses more than 11/9 M+4 bins. There exists sequences such that it uses 11/9 M bins. CS 223 Advanced Data Structures and Algorithms 18