Greedy Algorithms Chapter 5 Interval Scheduling Interval scheduling

Greedy Algorithms – Chapter 5

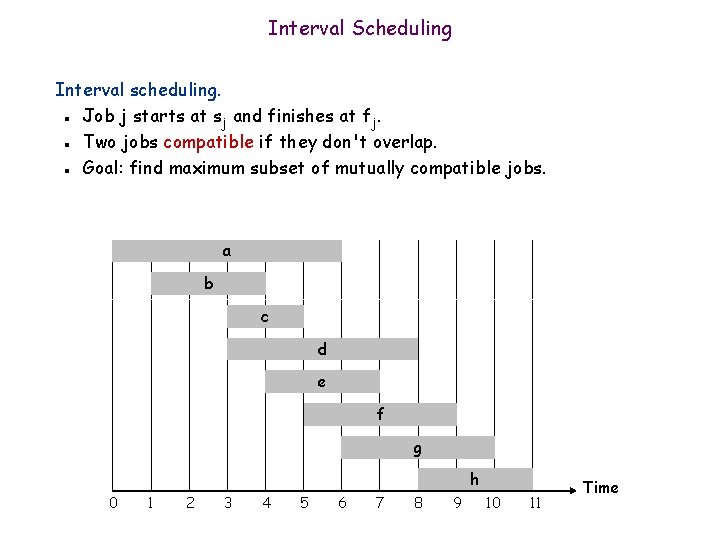
Interval Scheduling Interval scheduling. Job j starts at sj and finishes at fj. Two jobs compatible if they don't overlap. Goal: find maximum subset of mutually compatible jobs. n n n a b c d e f g h 0 1 2 3 4 5 6 7 8 9 10 11 Time

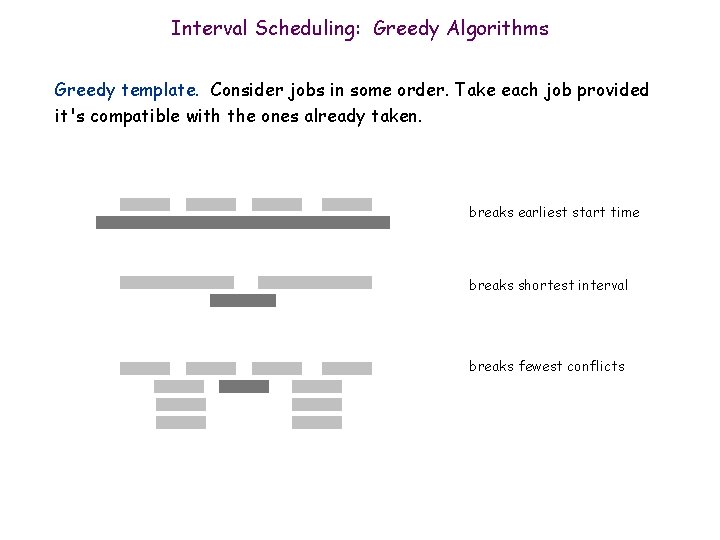
Interval Scheduling: Greedy Algorithms Greedy template. Consider jobs in some order. Take each job provided it's compatible with the ones already taken. n n [Earliest start time] Consider jobs in ascending order of start time sj. [Earliest finish time] Consider jobs in ascending order of finish time fj. [Shortest interval] Consider jobs in ascending order of interval length fj - sj. [Fewest conflicts] For each job, count the number of conflicting jobs cj. Schedule in ascending order of conflicts cj.

Interval Scheduling: Greedy Algorithms Greedy template. Consider jobs in some order. Take each job provided it's compatible with the ones already taken. breaks earliest start time breaks shortest interval breaks fewest conflicts

Interval Scheduling: Greedy Algorithm Greedy algorithm. Consider jobs in increasing order of finish time. Take each job provided it's compatible with the ones already taken. Sort jobs by finish times so that f 1 f 2 . . . fn. jobs selected A for j = 1 to n { if (job j compatible with A) A A {j} } return A Implementation. O(n log n). Remember job j* that was added last to A. Job j is compatible with A if sj fj*. n n

Interval Scheduling: Analysis Theorem. Greedy algorithm is optimal. Pf. (by contradiction) Assume greedy is not optimal, and let's see what happens. Let i 1, i 2, . . . ik denote set of jobs selected by greedy. Let j 1, j 2, . . . jm denote set of jobs in the optimal solution with i 1 = j 1, i 2 = j 2, . . . , ir = jr for the largest possible value of r. n n n job ir+1 finishes before j r+1 Greedy: i 1 ir OPT: j 1 j 2 jr ir+1 jr+1 why not replace job jr+1 with job ir+1? . . .

Interval Scheduling: Analysis Theorem. Greedy algorithm is optimal. Pf. (by contradiction) Assume greedy is not optimal, and let's see what happens. Let i 1, i 2, . . . ik denote set of jobs selected by greedy. Let j 1, j 2, . . . jm denote set of jobs in the optimal solution with i 1 = j 1, i 2 = j 2, . . . , ir = jr for the largest possible value of r. n n n job ir+1 finishes before j r+1 Greedy: i 1 ir ir+1 OPT: j 1 j 2 jr ir+1 . . . solution still feasible and optimal, but contradicts maximality of r.

4. 1 Interval Partitioning

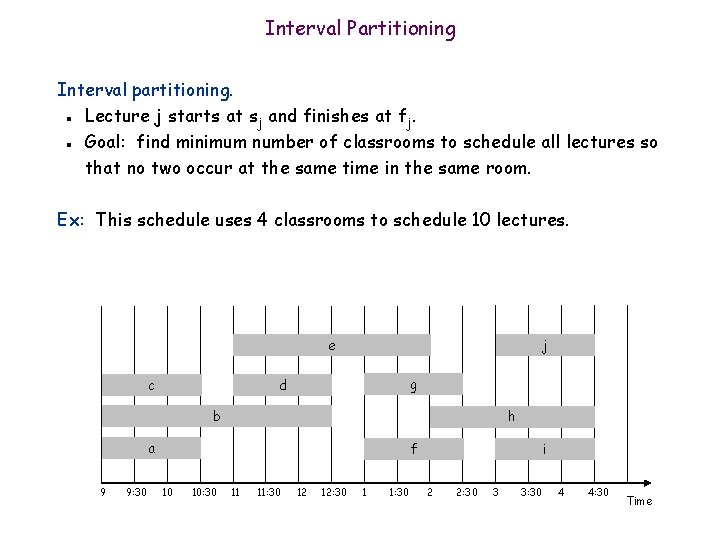
Interval Partitioning Interval partitioning. Lecture j starts at sj and finishes at fj. Goal: find minimum number of classrooms to schedule all lectures so that no two occur at the same time in the same room. n n Ex: This schedule uses 4 classrooms to schedule 10 lectures. e c j g d b h a 9 9: 30 f 10 10: 30 11 11: 30 12 12: 30 1 1: 30 i 2 2: 30 3 3: 30 4 4: 30 Time

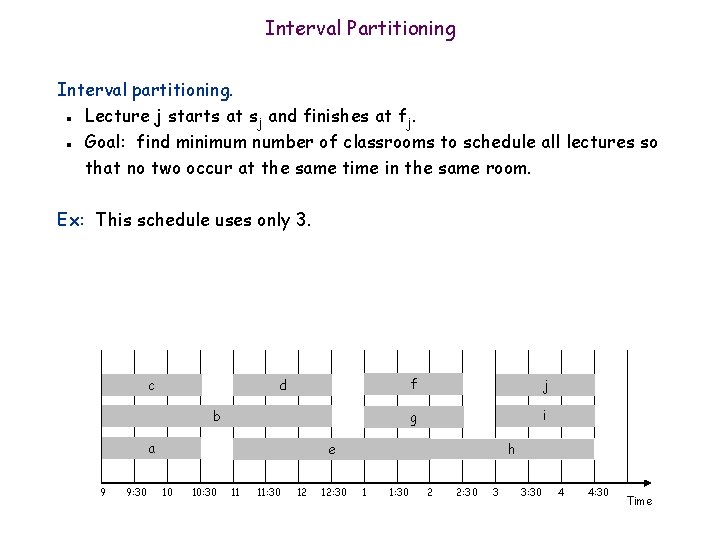
Interval Partitioning Interval partitioning. Lecture j starts at sj and finishes at fj. Goal: find minimum number of classrooms to schedule all lectures so that no two occur at the same time in the same room. n n Ex: This schedule uses only 3. c d b a 9 9: 30 f j g i h e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 Time

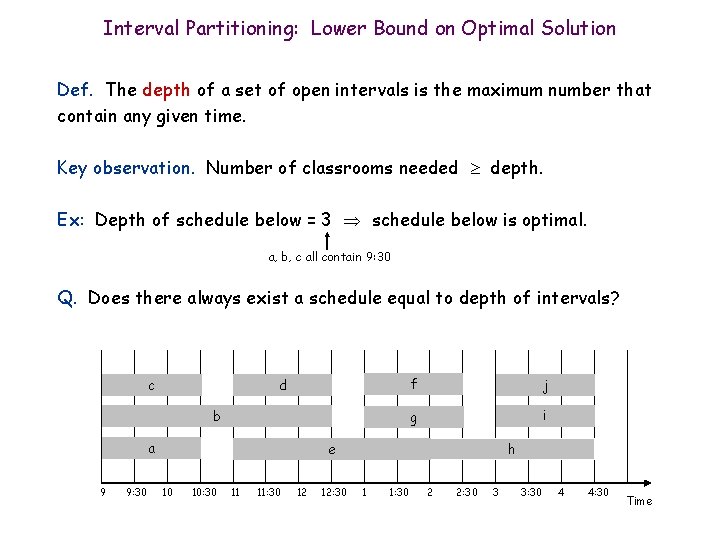
Interval Partitioning: Lower Bound on Optimal Solution Def. The depth of a set of open intervals is the maximum number that contain any given time. Key observation. Number of classrooms needed depth. Ex: Depth of schedule below = 3 schedule below is optimal. a, b, c all contain 9: 30 Q. Does there always exist a schedule equal to depth of intervals? c d b a 9 9: 30 f j g i h e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 Time

Interval Partitioning: Greedy Algorithm Greedy algorithm. Consider lectures in increasing order of start time: assign lecture to any compatible classroom. Sort intervals by starting time so that s 1 s 2 . . . sn. number of allocated classrooms d 0 for j = 1 to n if (lecture schedule else allocate schedule d d + } { j is compatible with some classroom k) lecture j in classroom k a new classroom d + 1 lecture j in classroom d + 1 1 Implementation. O(n log n). For each classroom k, maintain the finish time of the last job added. Keep the classrooms in a priority queue. n n

Interval Partitioning: Greedy Analysis Observation. Greedy algorithm never schedules two incompatible lectures in the same classroom. Theorem. Greedy algorithm is optimal. Pf. Let d = number of classrooms that the greedy algorithm allocates. Classroom d is opened because we needed to schedule a job, say j, that is incompatible with all d-1 other classrooms. Since we sorted by start time, all these incompatibilities are caused by lectures that start no later than sj. Thus, we have d lectures overlapping at time sj + . Key observation all schedules use d classrooms. ▪ n n n

Minimum Spanning Tree Spanning tree: A set of edges of a graph that forms a tree.

Minimum Spanning Trees

Minimum Spanning Trees

Minimum Spanning Trees

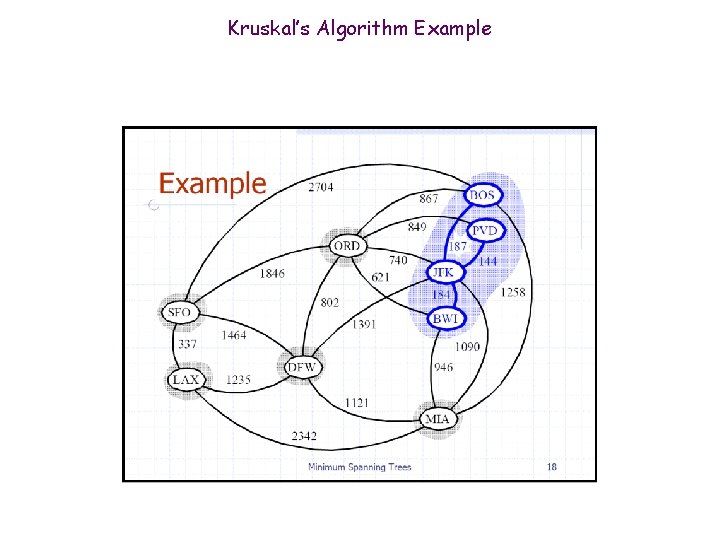
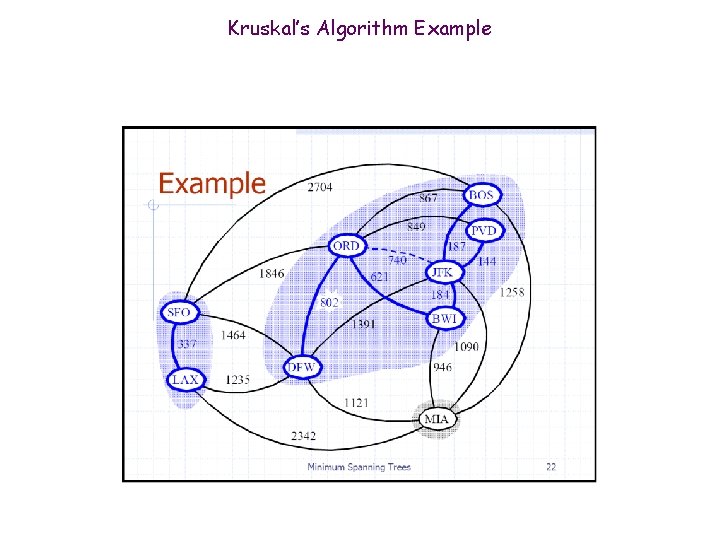
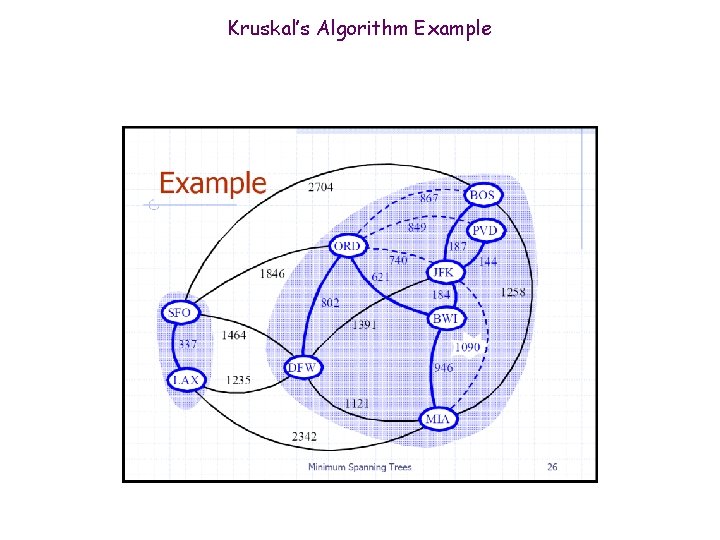
Kruskal’s Algorithm Example

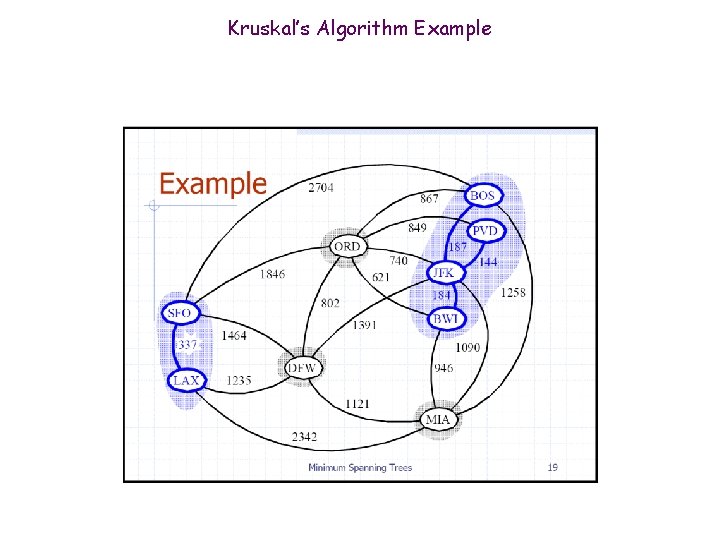
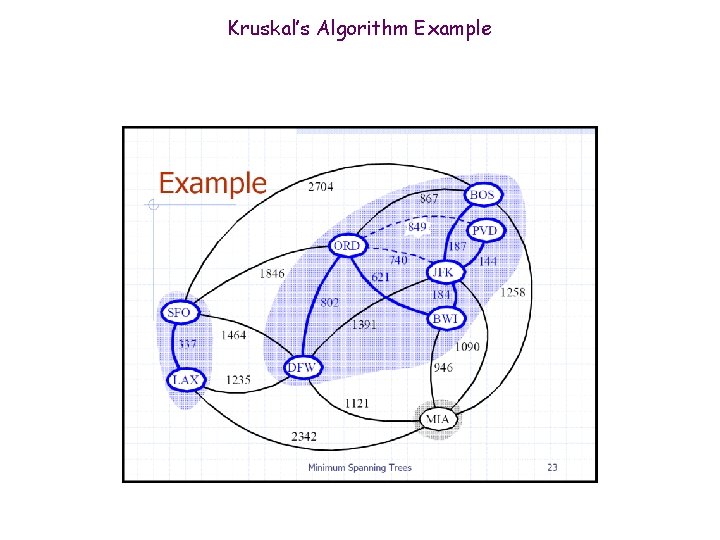
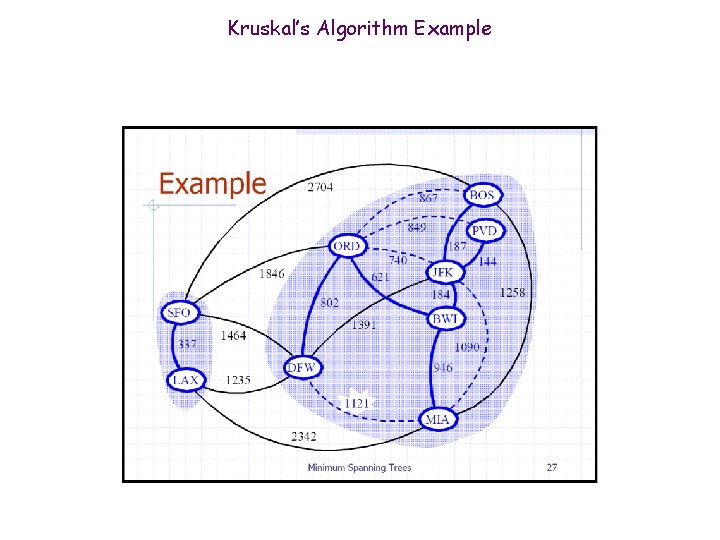
Kruskal’s Algorithm Example

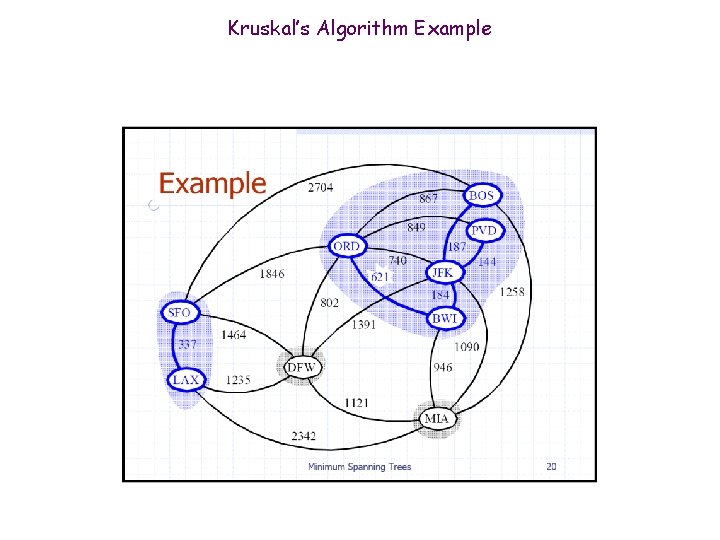
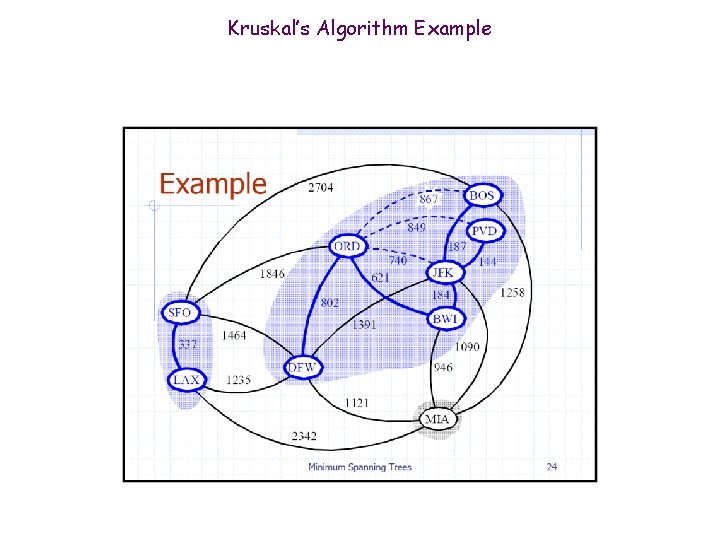
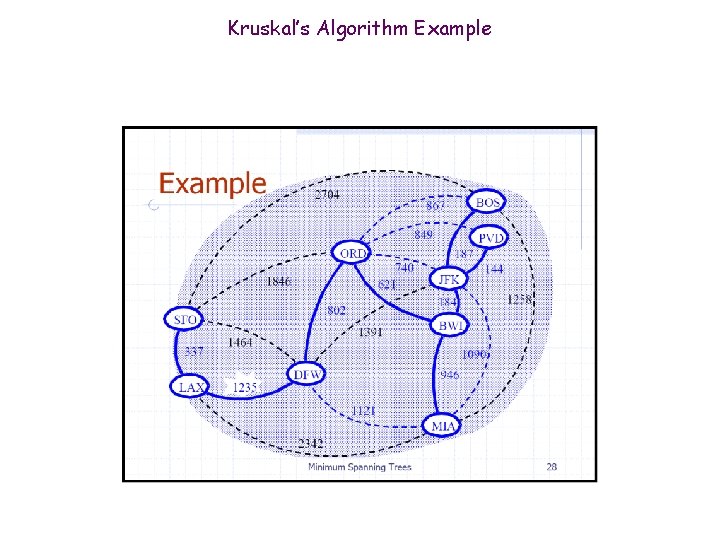
Kruskal’s Algorithm Example

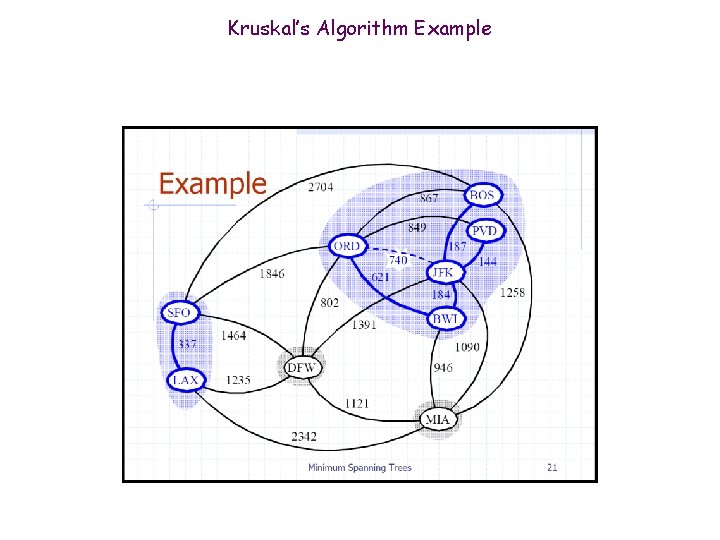
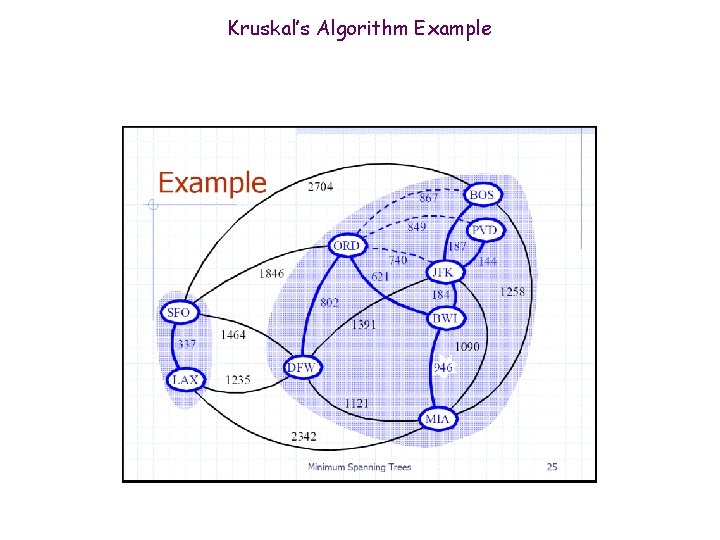
Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Kruskal’s Algorithm Example

Minimum Spanning Trees

Minimum Spanning Trees

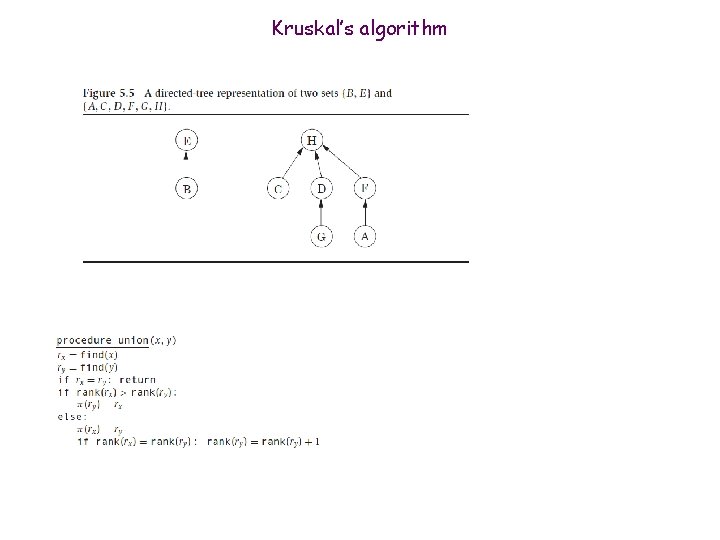
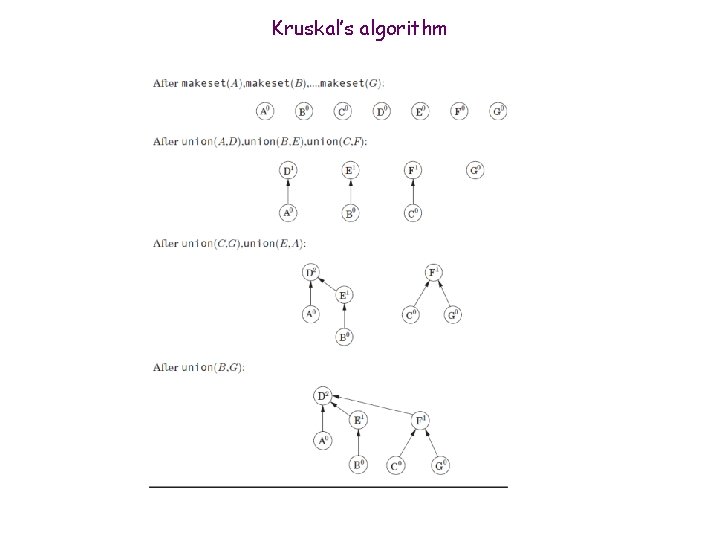
Kruskal’s algorithm

Kruskal’s algorithm

Kruskal’s algorithm

Application of MST: an example In the design of electronic circuitry, it is often necessary to make a set of pins electrically equivalent by wiring them together. To interconnect n pins, we can use n-1 wires, each connecting two pins. We want to minimize the total length of the wires. Minimum Spanning Trees can be used to model this problem. 37

Electronic Circuits: 38

Electronic Circuits: 39

Coding symbols of an alphabet Block coding: Ascii code is an example. Each symbol will be coded with 8 bits. Is this efficient?

valid vs. invalid code • Coding scheme should be such that the receiver of a stream of bits should be able to reconstruct the original string. • Not valid: A 0 B 10 C 11 Encoded message: 100. is it C or is it BA? and D 100

The algorithm can be implemented in O(n log n) time if there are n symbols. Used in almost all compression algorithms such as zip, jpeg etc.