Greedy Algorithm n GreedyActivitySelectorS f n Algorithm quicksort

Greedy Algorithm

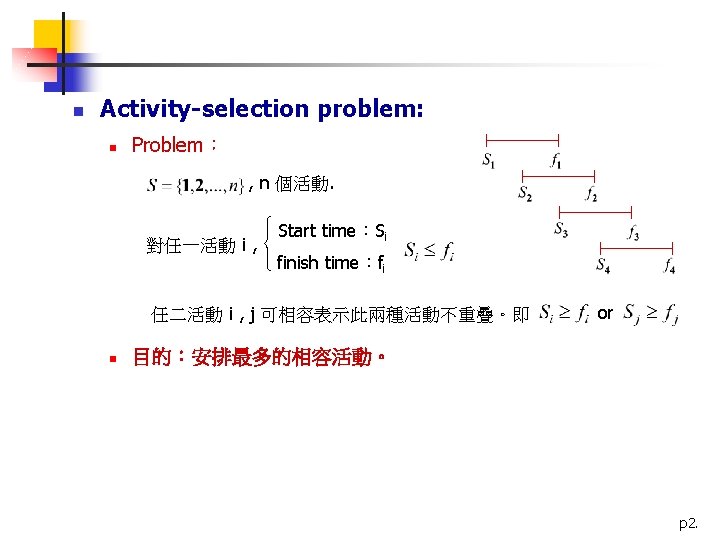
n Greedy-Activity-Selector(S, f)： n Algorithm： , 此可由 quicksort 達到 ~ 假設 Greedy-Activity-Selector(S, f) { n = length(S) ; A = {1} ; j=1; for i=2 to n do if then return A } n Complexity： n Thm：上述演算法可產生最多的相容活動。 p 3.

n Greedy 方法之要素： n 1. Globally optimal solution 可由選擇 local optimal solution 獲得。 n 2. 一最佳解包含子問題之最佳解。 ( 此與 Dynamic Programming 類似 ) p 4.

n 0 -1 knapsack problem：( NP complete ) n Problem： n items i-th item： worth weight dollars units A person carry W units. n n Goal：to carry as much value as possible. Fractional knapsack problem： n Problem： 同上，每一件東西可只取部分 ( 如 1/4, …. ) 依序由大而小排列 Example：W=50 item 1： item 2： item 3： 取 item 1 , item 2 及 2/3 的 item 3. p 5.

n Huffman codes： a b c d e f Frequency (x 1000) 45 13 12 16 9 5 Fixed-length codeword 000 001 010 011 100 101 variable-length codeword 0 101 100 111 1100 若用 fixed-length codeword： 總共有 若用 variable-length codeword：總共有 p 6.

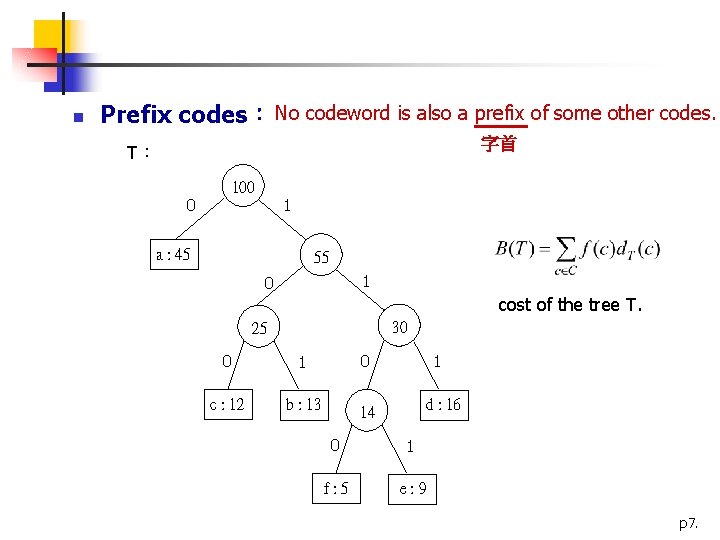
n Prefix codes： No codeword is also a prefix of some other codes. 字首 T： 0 100 1 a : 45 55 1 0 cost of the tree T. 30 25 0 1 0 c : 12 b : 13 14 1 d : 16 0 1 f: 5 e: 9 p 7.

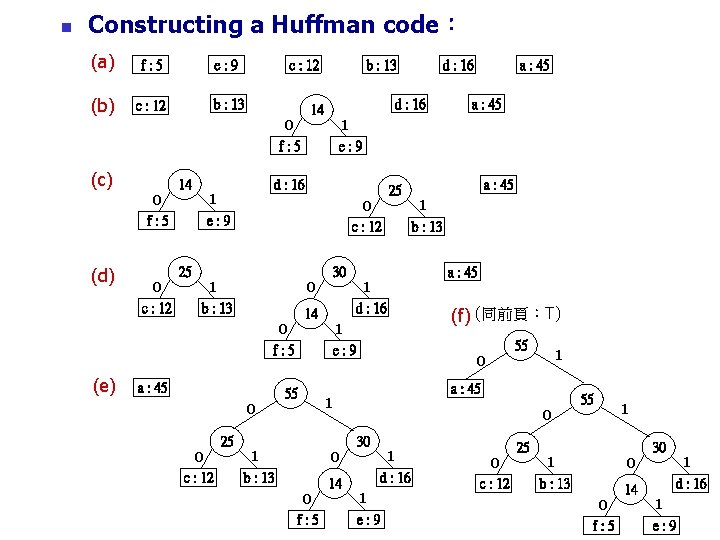
n Constructing a Huffman code： (a) f: 5 e: 9 (b) c : 12 b : 13 c : 12 0 f: 5 (c) 0 f: 5 (d) 0 c : 12 14 25 1 e: 9 0 14 a : 45 0 0 c : 12 25 55 1 b : 13 30 25 1 d : 16 1 e: 9 a : 45 14 a : 45 1 b : 13 a : 45 (f) (同前頁：T) 0 55 1 a : 45 1 0 0 f: 5 a : 45 1 e: 9 0 c : 12 1 b : 13 d : 16 14 d : 16 0 f: 5 (e) b : 13 0 30 1 d : 16 1 e: 9 0 c : 12 25 55 1 b : 13 1 0 0 f: 5 14 30 1 d : 16 1 e: 9

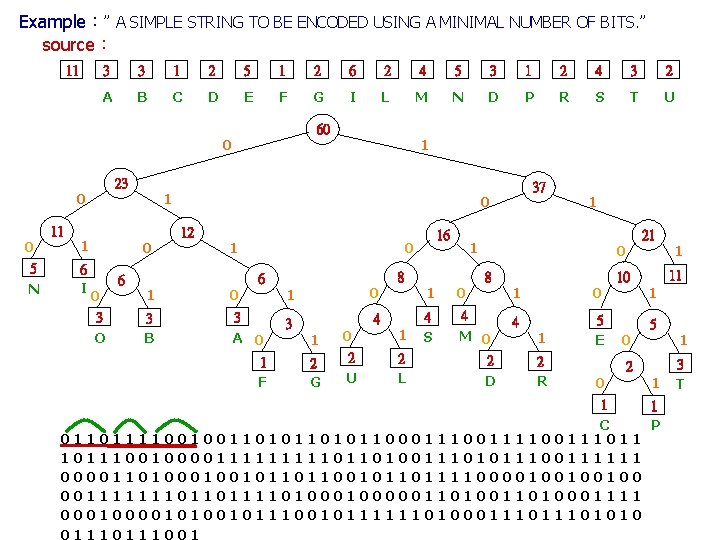
Example：” A SIMPLE STRING TO BE ENCODED USING A MINIMAL NUMBER OF BITS. ” source： 11 3 3 1 2 5 1 2 6 2 4 5 3 1 2 4 3 2 A B C D E F G I L M N D P R S T U 60 0 23 0 0 5 N 11 1 6 I 1 0 0 3 O 6 1 37 0 12 1 16 0 6 8 1 21 1 8 0 1 10 11 1 0 1 0 1 3 B 3 A 0 3 4 4 S 4 M 0 4 5 E 5 1 F 1 2 G 0 2 U 1 2 L 2 D 1 2 R 0 0 1 2 3 T 1 1 1 C P 011011110010011010110001111001110111001000011111011010011101011100111111 00001101001011011001011011110000100100100 00111111101101111010000011010001111 00010100101111110100011101010 0111001

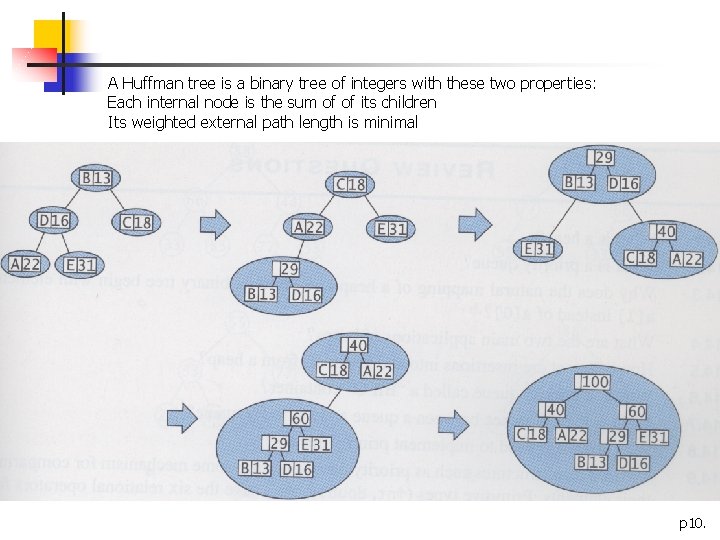
A Huffman tree is a binary tree of integers with these two properties: Each internal node is the sum of of its children Its weighted external path length is minimal p 10.

Algorithm: Generating a Huffman code Input: a sequence of characters output: a bit code for the input characters Postconditions: the bit code has the unique prefix property and is optimal 1. Tally the frequencies of the input characters 2. Load the letter-frequency pairs into a min priority queue 3. Coalesce the pairs into a Huffman tree 4. Encode the character at each leaf with the bit sequence along root-to-leaf path p 11.

n Huffman(C)： n Algorithm： Huffman(C) { // Q：priority queue for i=1 to n-1 do { z = allocate-Node() ; x = left(z) = Extract-min(Q) ; y = right(z) = Extract-min(Q) ; f(z) = f(x) + f(y) ; Insert(Q , z) ; } return Extract-min(Q) ; } n Complexity： p 12.

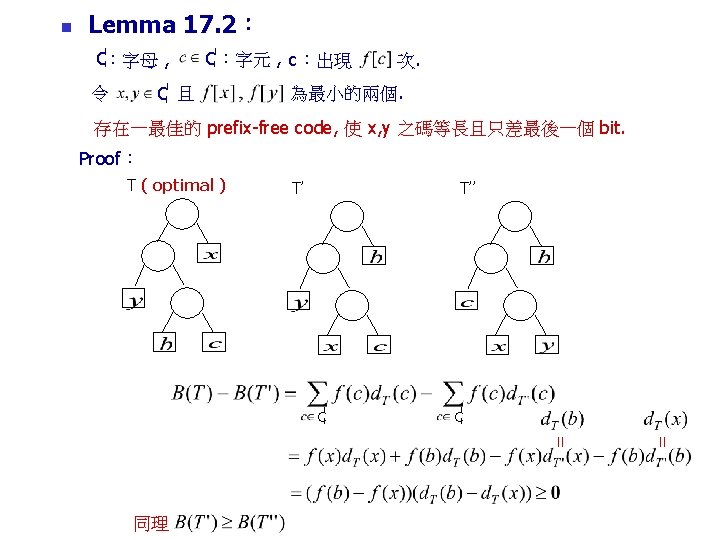
n Lemma 17. 3： 令 T：full binary tree representing an optimal prefix code over C. leaves T’ represents an optimal prefix code for C’. Proof： 對任一 C 若 T’ 不是 C’ 的最佳 prefix code. 則可找到 T’’ 使 B(T’’) < B(T’) T 是 C 之最佳之 prefix code.

n Matroids： n n 1. S：有限非空集合 2. X：為 S 的部分集合所形成之集合 ( 即 X 的元素為集合 ) independent subset 並滿足：若 且 則 ( hereditary property ) n 3. 若 且 則存在 使得 ( exchange property ) Example：Matric matroid if rows in I are linearly independent. n Graphic matroid： 為一 graph. n n 且 A：acyclic. ( i. e. A forms a forest ) p 16.

n Thm 17. 6： All maximal independent subsets in a matroid have the same size. , A is maximal if it has no extension. Proof： 即不存在 使得 假設 A：maximal independent subset. B：maximal independent subset 且 存在 使得 A 為 maximal. p 18.

n Weighted Matroid： n Definition： , weight function：w(x) for each n Greedy algorithms on a weighted matroid n Problem： Given , find has maximal possible weight. Example：Minimum Spanning Tree ：weight function defined on E; . Define , and Let A be a maximal independent set in X. Then A corresponds to a spanning tree in G. p 19.

n Algorithm： Greedy(M, w) { Sort S[M] into nonincreasing order by weight w ; For each , taken in nonincreasing order by weight w(x) ; do if then Return A } 若 則上述需 步驟。 p 20.

n Thm 17. 8： 為任一 matroid. 令 若 且 x 不為 extension. 之 extension, 則 x 不為任一 independent set 之 Proof： 假設 x 為 A 之 extension 但不為 independent. 之 extension. x 為 A 之 extension. 由假設 x 不是 之 extension. p 22.

n Thm 17. 9(Matroids optimal-substructure)： 令 x 為 Greedy 演算法中第一個被選入的元素. 尋找 M 中包含 x 之 maximum-weight independent subset 可以 被轉化為尋找 matroid 之 maximum weight ind. Set. Proof： 若 且 A：maximum weighted 且 反之若 又 則 故由 M 中含 x 之 maximum-weight solution 可找到 M’ 之 maximum-weight solution. 反之亦然. n Thm 17. 10： 給定 Proof： , 則 Greedy(M, w) 可以找到 optimal solution. p 23.

n A task-scheduling problem： n S={1, 2, …. . , n} n Deadlines： n n unit-time tasks. task i 需在 di 前完成. Penalties： 若 task i 不能在 di 前完成，則罰 wi 若 task i 能在 di 前完成著無 penalty. 目標：安排一執行順序使 penalty 最小. Example： 1 2 3 4 5 6 7 4 2 4 3 1 4 6 70 60 50 40 30 20 10 Schedule：< 2 4 1 3 7 5 6 > penalty 20+30=50. p 24.

n Def： n 在一 schedule 中： n n late task：if it finishes after its deadline. early task：if it finishes before its deadline. Early-first form：early tasks precede the late tasks. Canonical form：same as early-first form and the early tasks are scheduled in order of nondecreasing deadlines. k 若 i k+1 j i, j：early task n n n k j k+1 i a set A of task is independent：若存在一 schedule 使得 A 中無 late schedule. 故任一 schedule 中之 early tasks 形成一 independent set. 令 X 表所有 independent set 之集合. 如何判定一 tasks 集合是否為 independent？ t=1, 2, …, n ，令 Nt(A) 表 A 中之 tasks 其 deadline t.

n Lemma 17. 11： 令 A：tasks 所形成之集合. 則下列序列等價 1. A：independent. 2. For t=1, 2, …n， 3. 若 A 中之 tasks 依 deadlines ( nondecreasing ) 排序，則無 late task. Proof： 若 , 則 A 中存在 late task. 故 顯然. p 26.

n Thm 17. 12： S={ unit tasks with deadline } X={ independent sets of tasks } (S, X) is a matroid. Proof： (1) clearly. (2) 由上述 independent set 之定義知其滿足 matroid 之第 2 個條件。 (3) 且 p 27.

Solution by Greedy Algorithm n Sort w 1, …. . , wn in decreasing order n Check A {i} X ? n Time complexity: O(n*n). p 28.

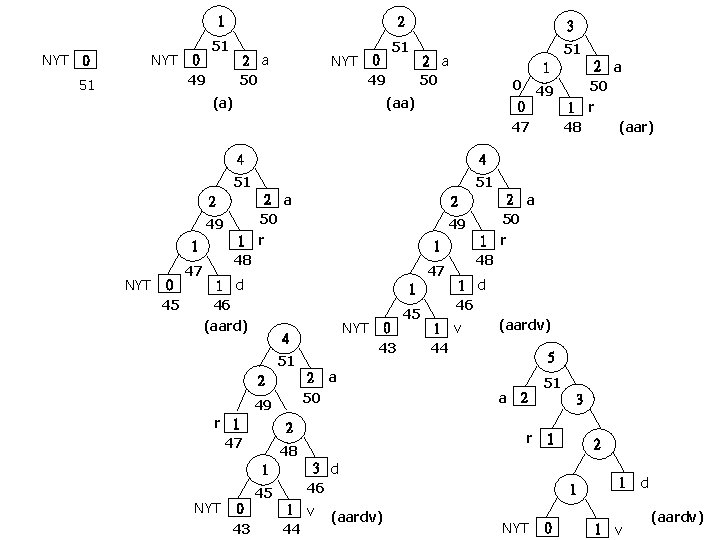
NYT 0 49 0 51 1 2 51 51 2 a 50 NYT 0 49 (a) 0 45 47 4 51 51 1 48 2 a 50 r 2 49 47 1 (aard) NYT 0 43 4 51 2 2 49 50 r 1 47 0 43 1 d 46 1 v 44 (aardv) 5 a 2 r 48 45 45 2 a 50 r a 2 1 1 48 1 1 d 46 NYT 2 a 0 49 50 0 1 r 47 48 (aar) 1 4 49 NYT 51 2 a 50 (aa) 2 1 3 51 3 d 46 1 v 44 (aardv) 2 1 NYT 0 1 1 v d (aardv)

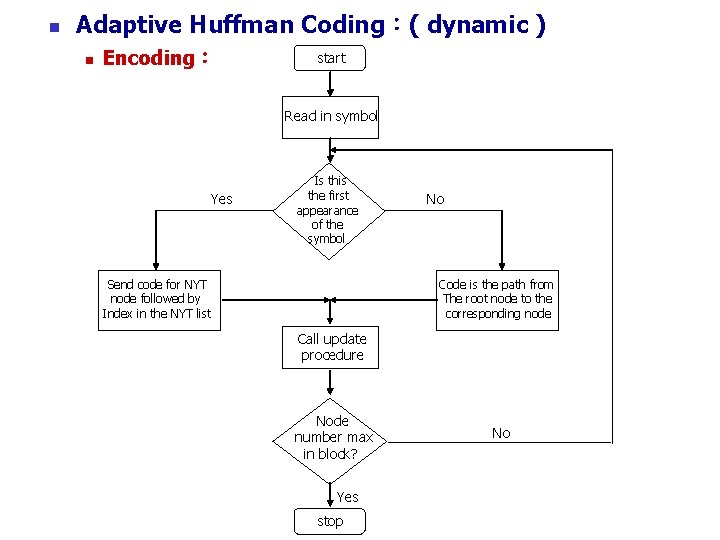
n Adaptive Huffman Coding：( dynamic ) n Encoding： start Read in symbol Yes Is this the first appearance of the symbol Send code for NYT node followed by Index in the NYT list No Code is the path from The root node to the corresponding node Call update procedure Node number max in block? Yes stop No

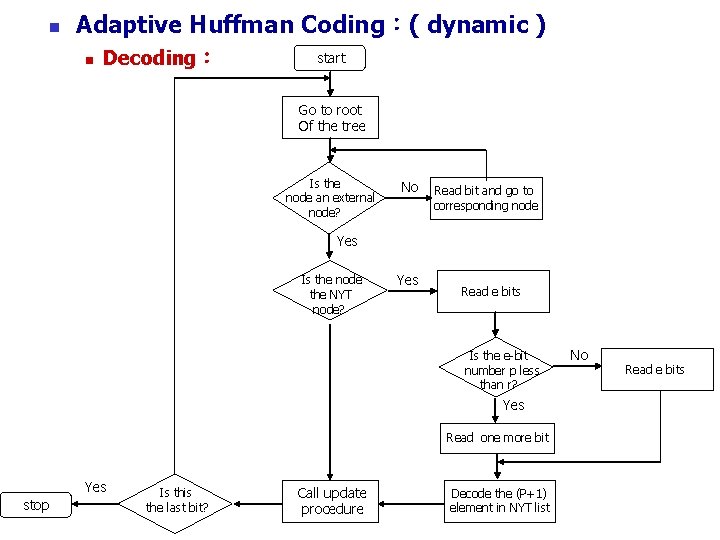
n Adaptive Huffman Coding：( dynamic ) n Decoding： start Go to root Of the tree Is the node an external node? No Read bit and go to corresponding node Yes Is the node the NYT node? Yes Read e bits Is the e-bit number p less than r? Yes Read one more bit Yes stop Is this the last bit? Call update procedure Decode the (P+1) element in NYT list No Read e bits

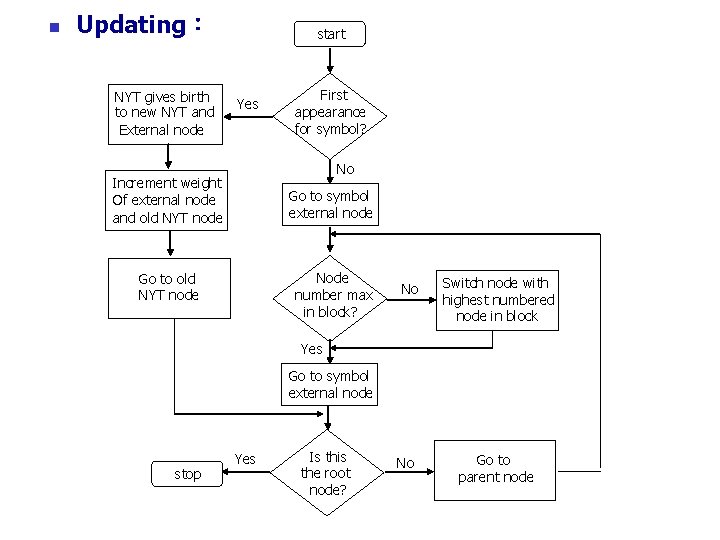
n Updating： NYT gives birth to new NYT and External node start Yes First appearance for symbol? No Increment weight Of external node and old NYT node Go to symbol external node Node number max in block? Go to old NYT node No Switch node with highest numbered node in block Yes Go to symbol external node stop Yes Is this the root node? No Go to parent node