Greedy Algorithm CSCI 385 Data Structures Analysis of

Greedy Algorithm CSCI 385 Data Structures & Analysis of Algorithms Lecture note Sajedul Talukder

Optimization Problems • A problem that may have many feasible solutions. • Each solution has a value • In maximization problem, we wish to find a solution to maximize the value • In the minimization problem, we wish to find a solution to minimize the value

Greedy Algorithm • Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. • In many problems, a greedy strategy does not usually produce an optimal solution. The problems where choosing locally optimal also leads to global solution are best fit for Greedy. • Greedy choice property • Make whatever choice seems best at the moment and then solve the subproblems that arise later. • Optimal substructure • A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to the sub-problems.

Interval Scheduling

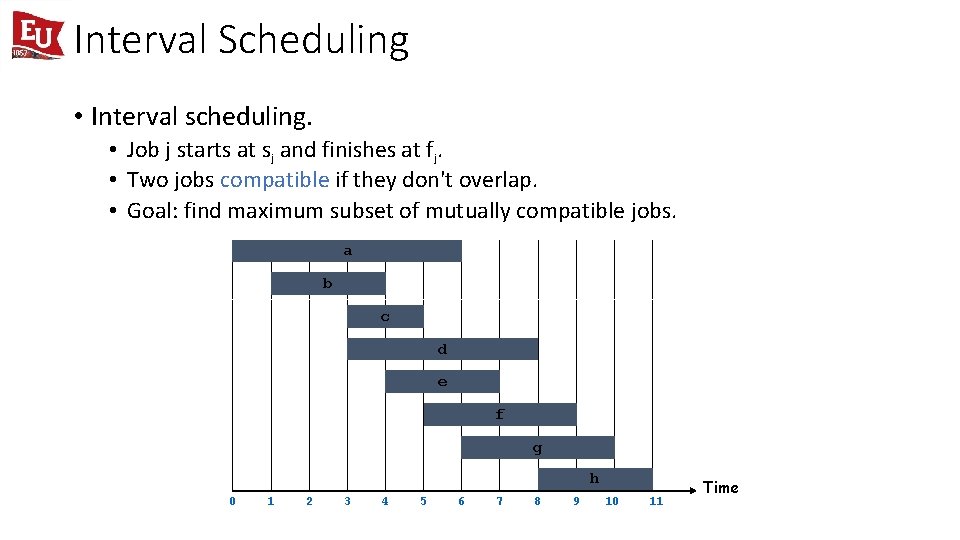
Interval Scheduling • Interval scheduling. • Job j starts at sj and finishes at fj. • Two jobs compatible if they don't overlap. • Goal: find maximum subset of mutually compatible jobs. a b c d e f g h 0 1 2 3 4 5 6 7 8 9 10 11 Time

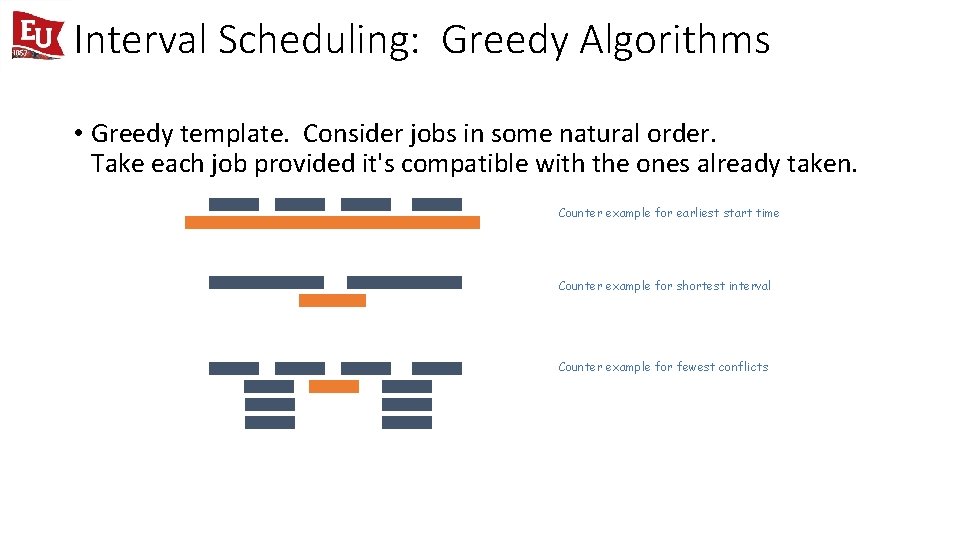
Interval Scheduling: Greedy Algorithms • Greedy template. Consider jobs in some natural order. Take each job provided it's compatible with the ones already taken. • [Earliest start time] Consider jobs in ascending order of sj. • [Earliest finish time] Consider jobs in ascending order of fj. • [Shortest interval] Consider jobs in ascending order of fj - sj. • [Fewest conflicts] For each job j, count the number of conflicting jobs cj. Schedule in ascending order of cj.

Interval Scheduling: Greedy Algorithms • Greedy template. Consider jobs in some natural order. Take each job provided it's compatible with the ones already taken. Counter example for earliest start time Counter example for shortest interval Counter example for fewest conflicts

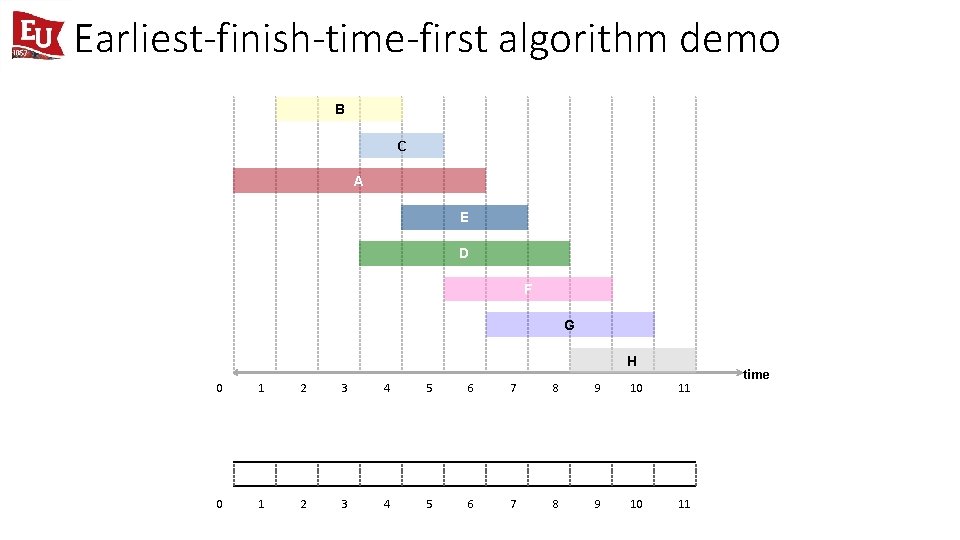
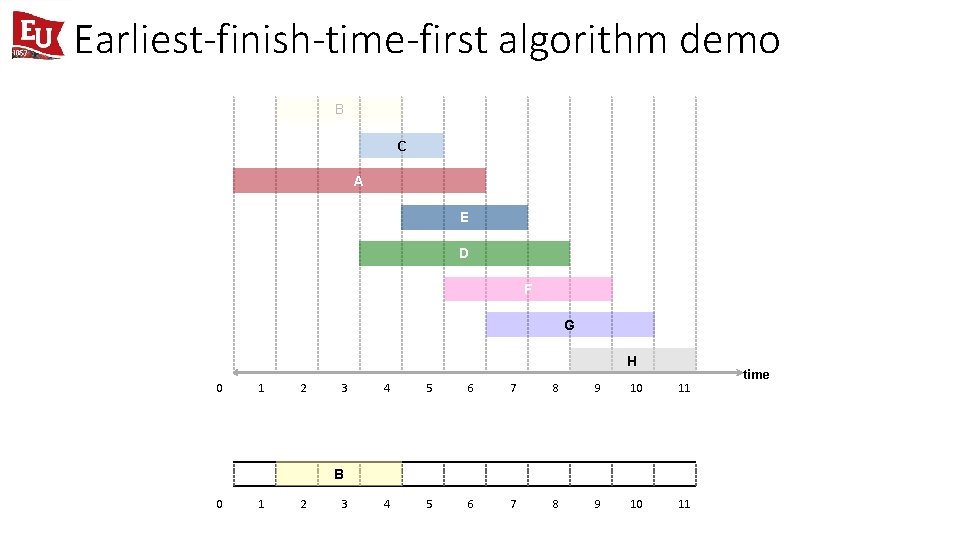
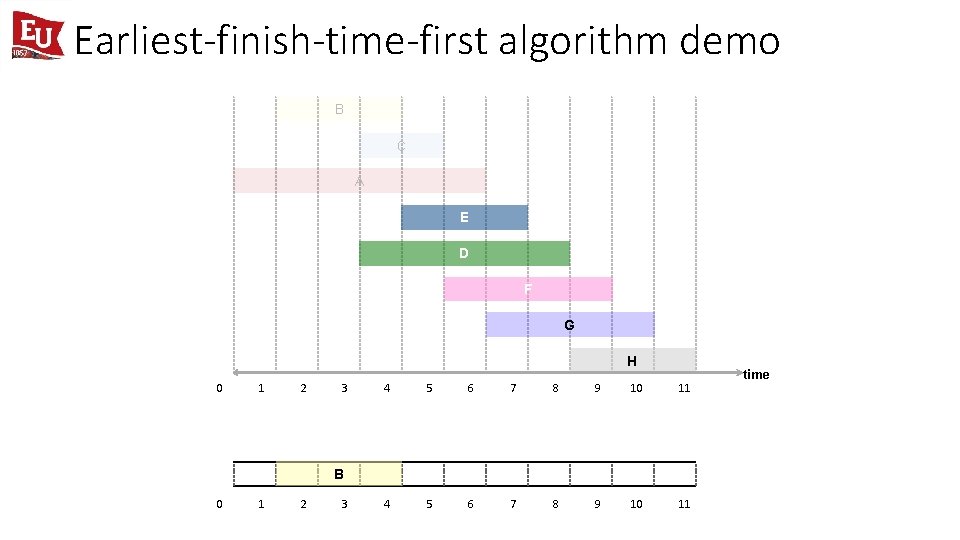
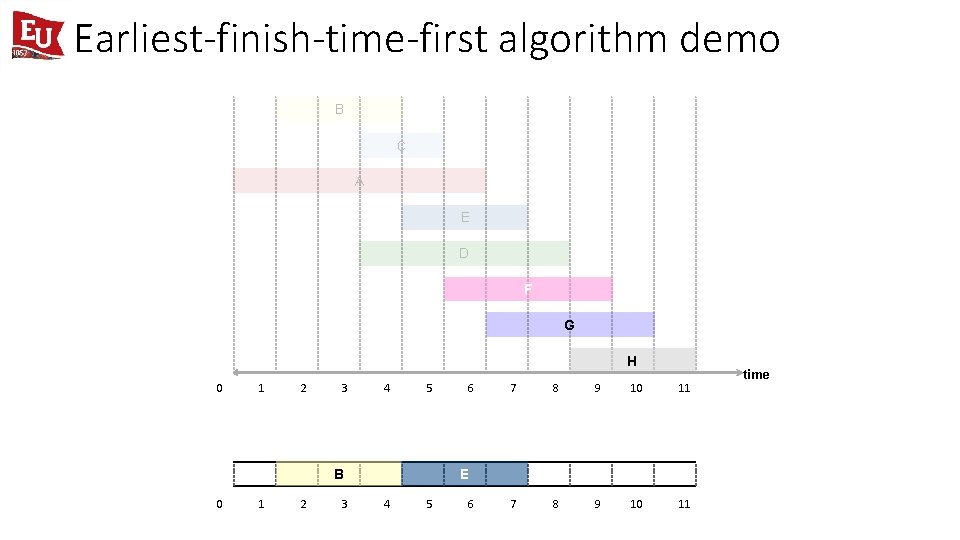
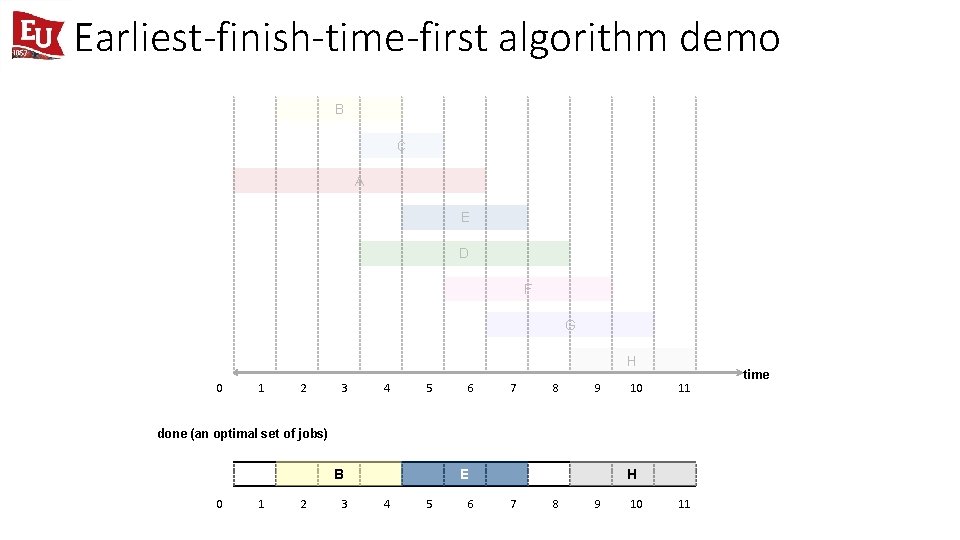
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 time

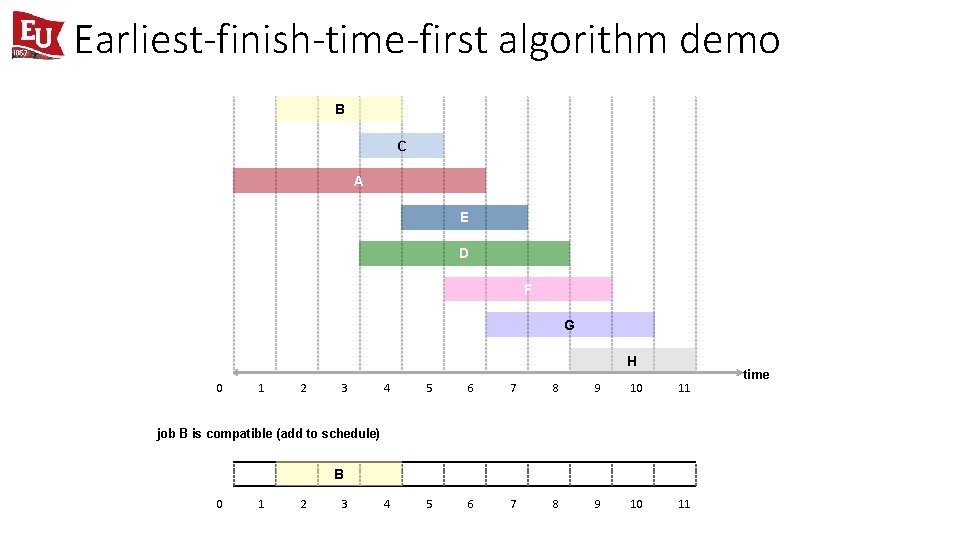
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job B is compatible (add to schedule) B 0 1 2 3 time

Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 B 0 1 2 3 time

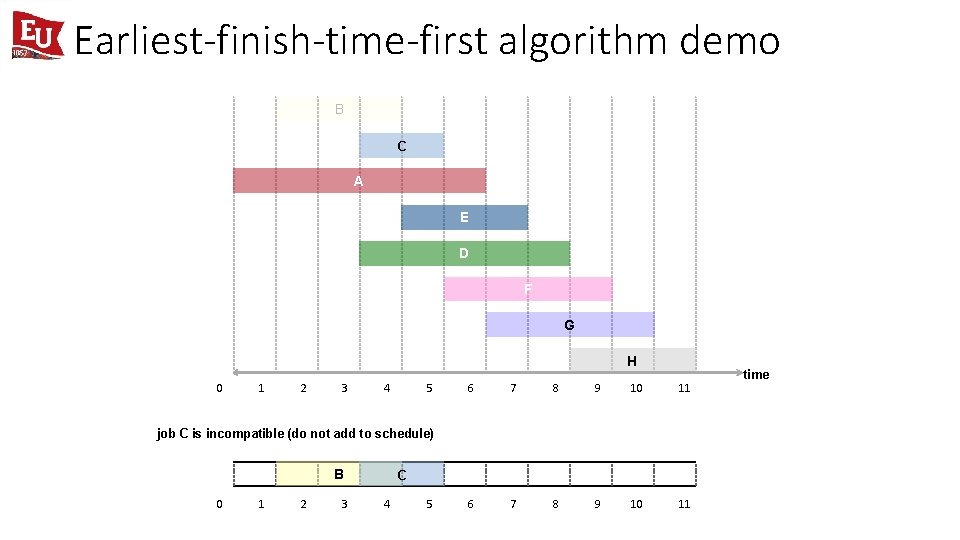
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job C is incompatible (do not add to schedule) B 0 1 2 3 C 4 5 time

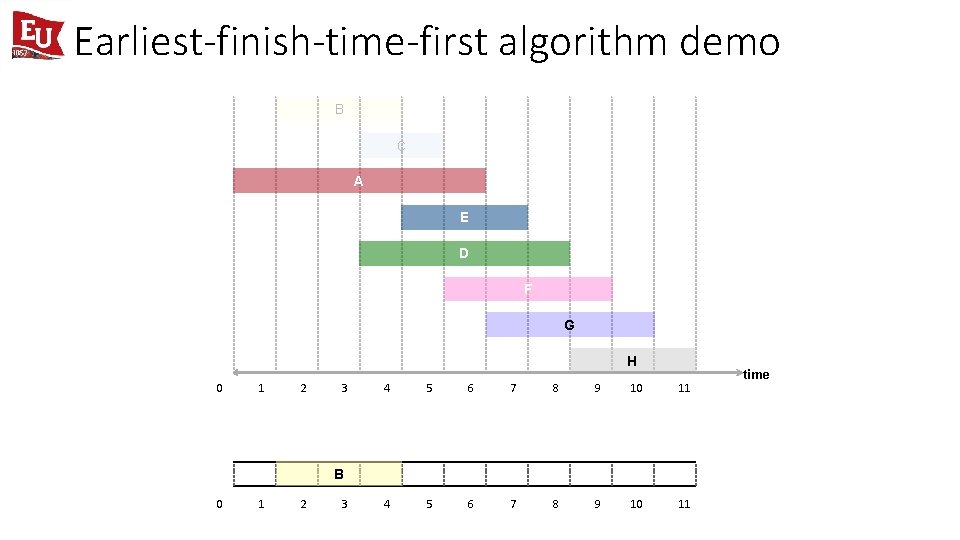
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 B 0 1 2 3 time

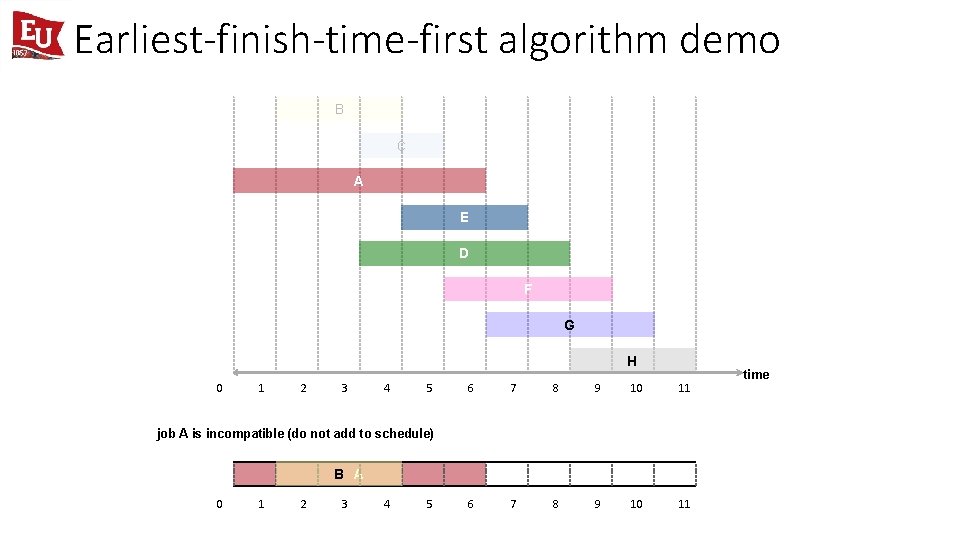
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job A is incompatible (do not add to schedule) B A 0 1 2 3 4 5 time

Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 B 0 1 2 3 time

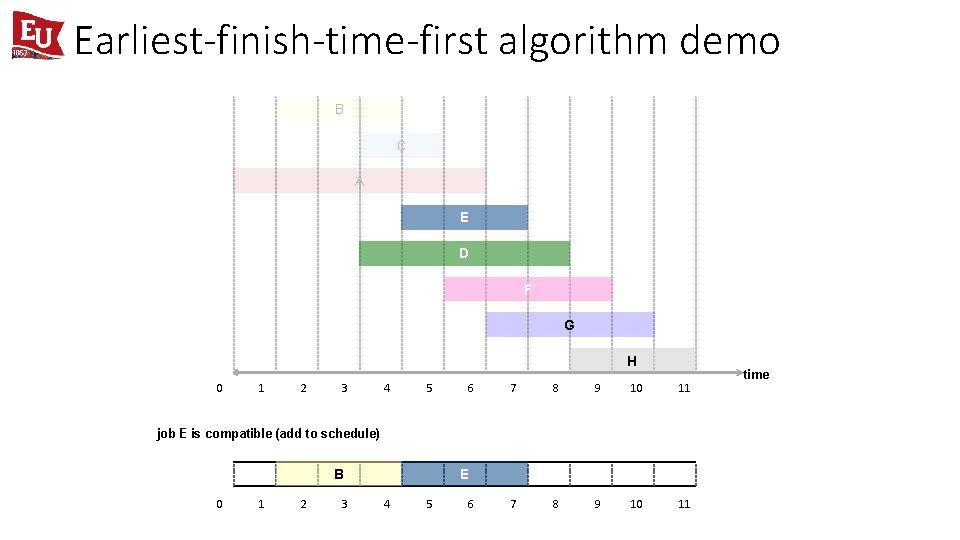
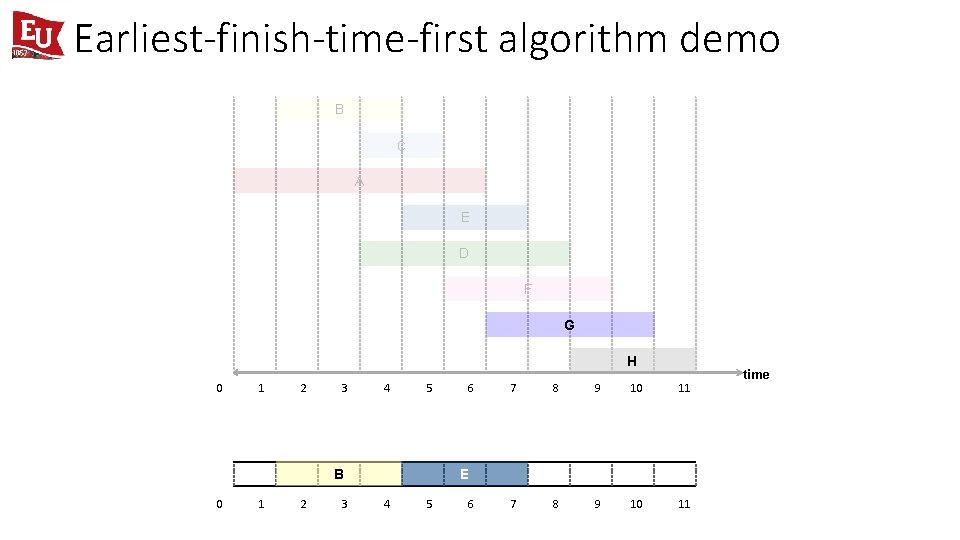
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job E is compatible (add to schedule) B 0 1 2 3 E 4 5 6 time

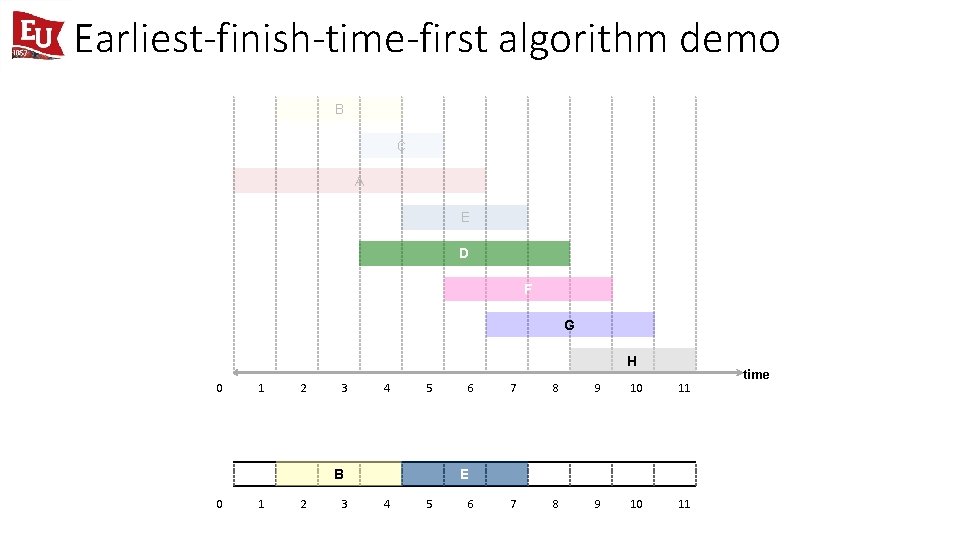
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 B 0 1 2 3 6 7 8 9 10 11 E 4 5 6 time

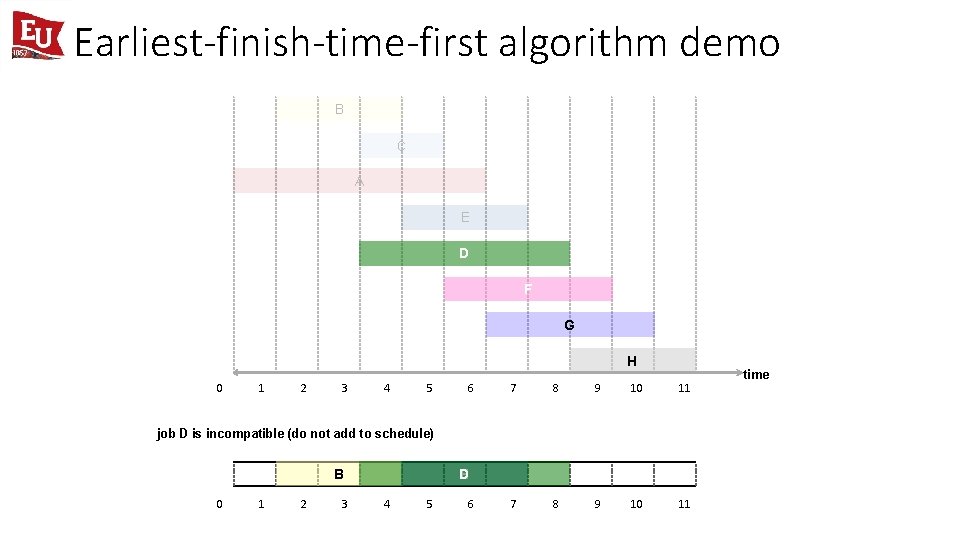
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job D is incompatible (do not add to schedule) B 0 1 2 3 D E 4 5 6 time

Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 B 0 1 2 3 6 7 8 9 10 11 E 4 5 6 time

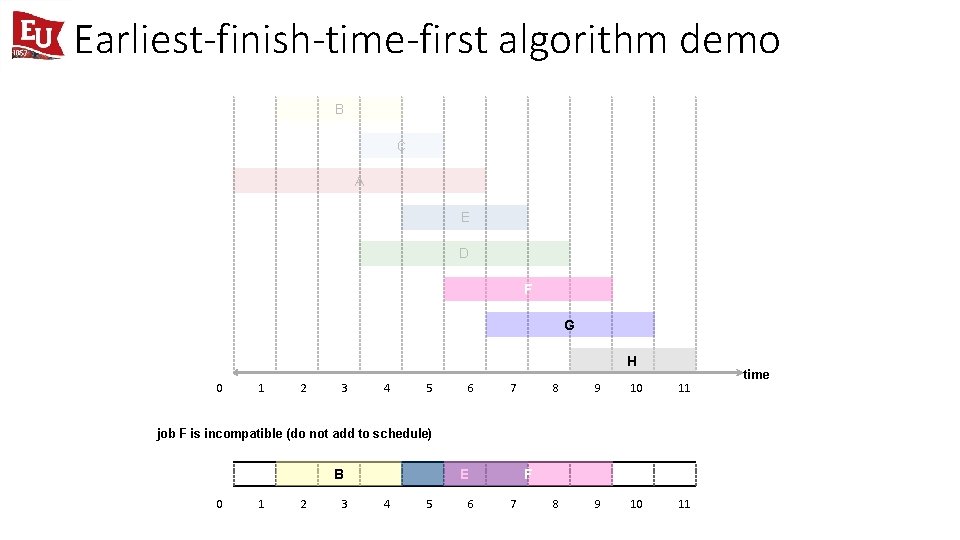
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job F is incompatible (do not add to schedule) B 0 1 2 3 E 4 5 6 F 7 time

Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 B 0 1 2 3 6 7 8 9 10 11 E 4 5 6 time

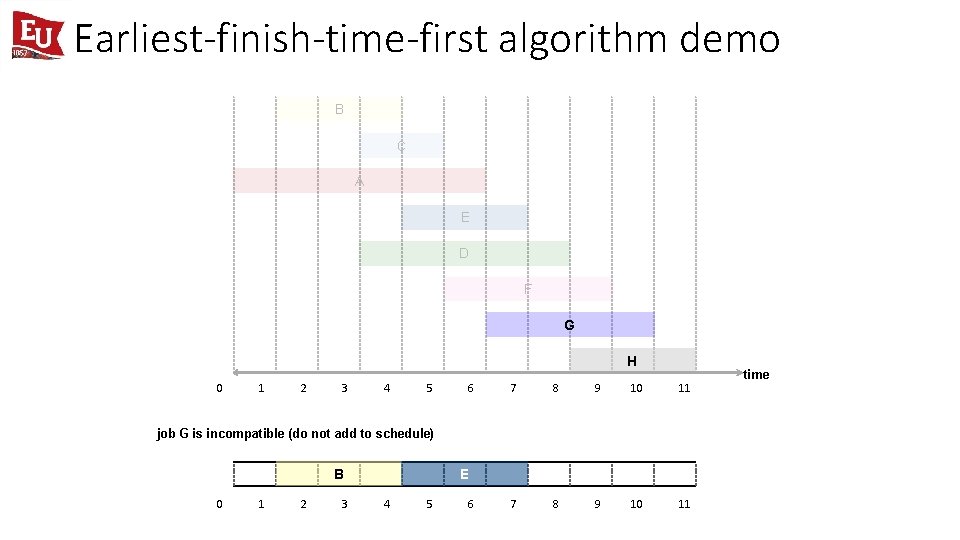
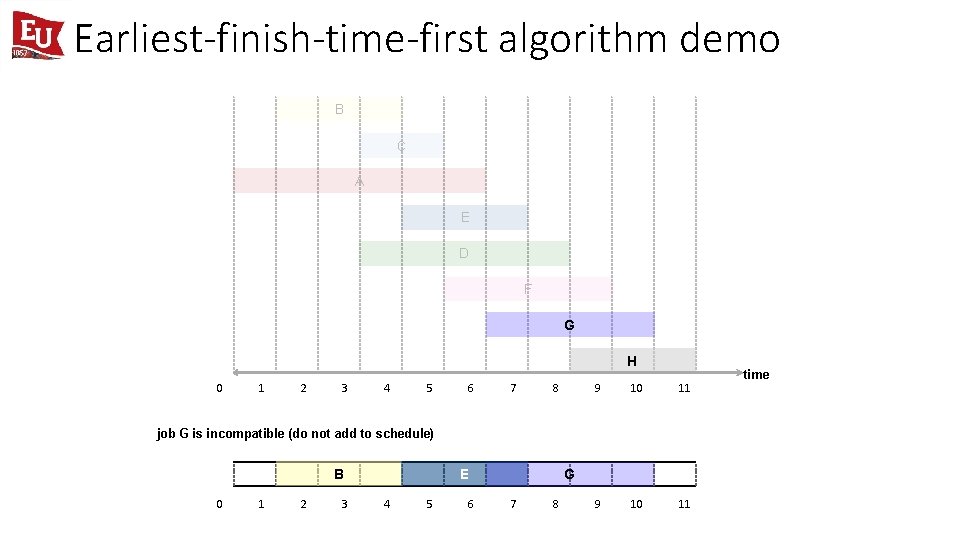
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job G is incompatible (do not add to schedule) B 0 1 2 3 E 4 5 6 time

Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job G is incompatible (do not add to schedule) B 0 1 2 3 E 4 5 6 G 7 8 time

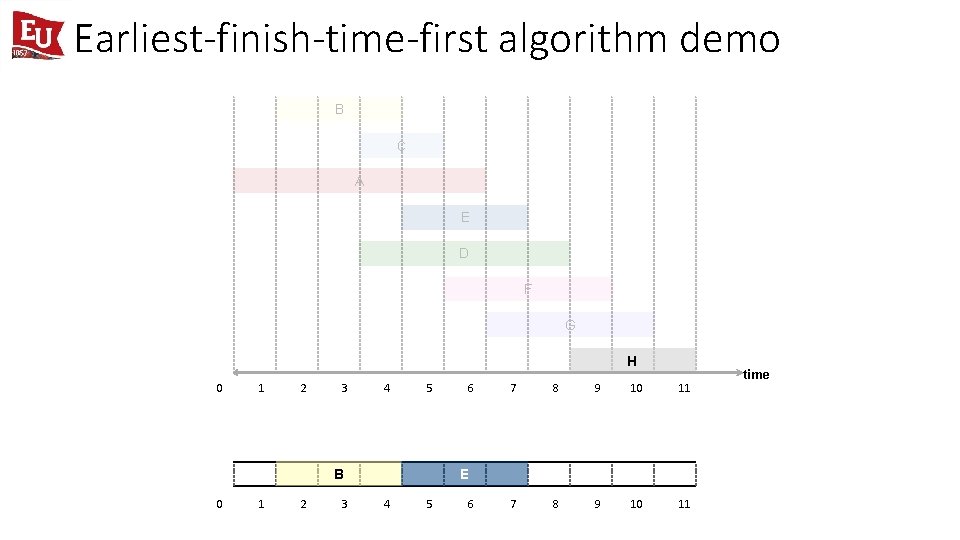
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 B 0 1 2 3 6 7 8 9 10 11 E 4 5 6 time

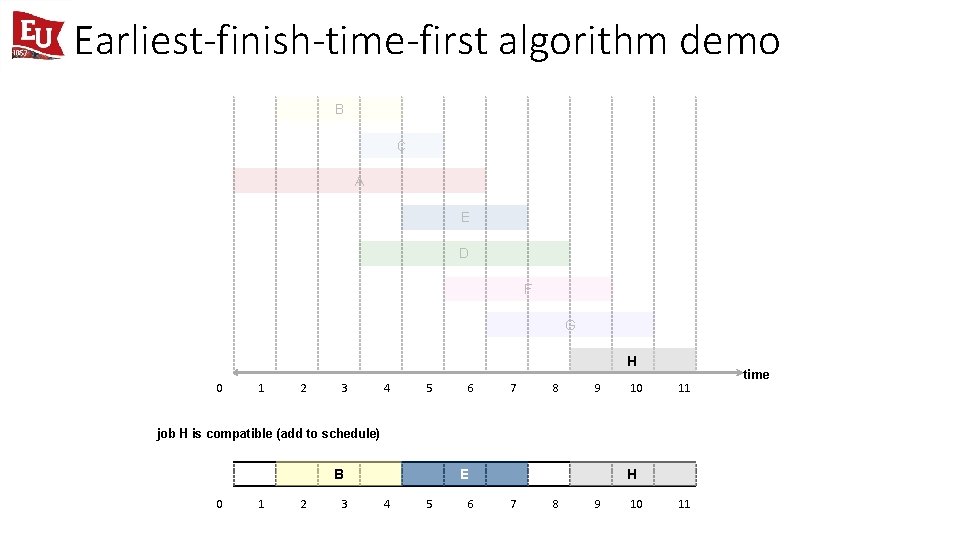
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 job H is compatible (add to schedule) B 0 1 2 3 E 4 5 6 H 7 8 9 10 11 time

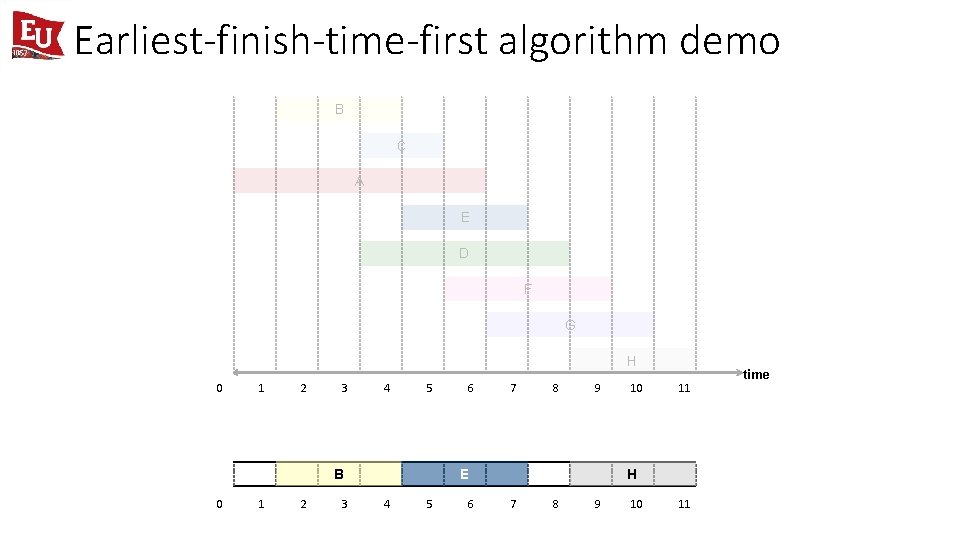
Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 B 0 1 2 3 6 7 8 9 E 4 5 6 10 11 H 7 8 9 10 11 time

Earliest-finish-time-first algorithm demo B C A E D F G H 0 1 2 3 4 5 6 7 8 9 10 11 done (an optimal set of jobs) B 0 1 2 3 E 4 5 6 H 7 8 9 10 11 time

Interval Scheduling: Greedy Algorithm • Greedy algorithm. Consider jobs in increasing order of finish time. Take each job provided it's compatible with the ones already taken. Sort jobs by finish times so that f 1 f 2 . . . fn. set of jobs selected S for j = 1 to n { if (job j compatible with S) S S {j} } return S • Implementation. O(n log n) sorting time of finishing time of n jobs. • Remember job j* that was added last to S. • Job j is compatible with A if s j fj*. O(n) time to go through the sorted list of n jobs 26

Interval Partitioning

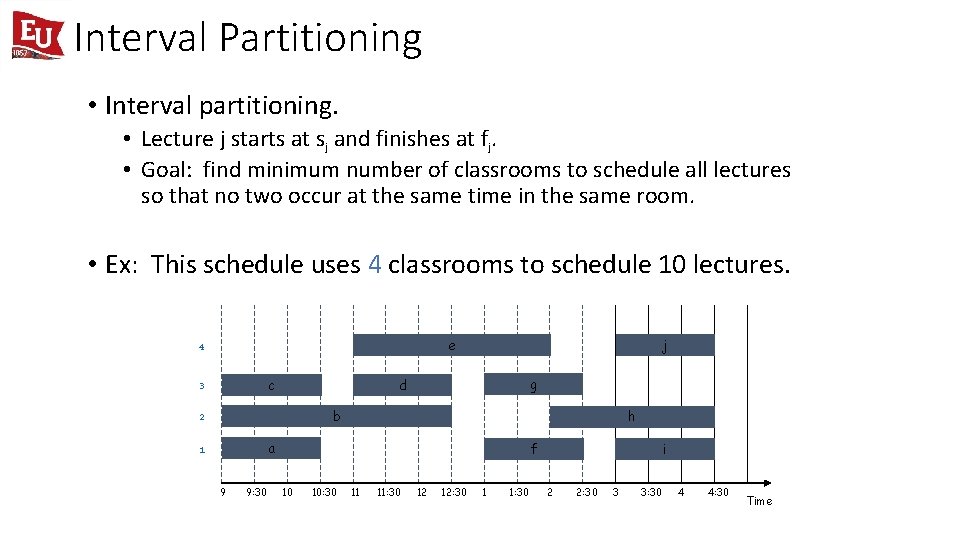
Interval Partitioning • Interval partitioning. • Lecture j starts at sj and finishes at fj. • Goal: find minimum number of classrooms to schedule all lectures so that no two occur at the same time in the same room. • Ex: This schedule uses 4 classrooms to schedule 10 lectures. e 4 c 3 j g d b 2 h a 1 9 9: 30 f 10 10: 30 11 11: 30 12 12: 30 1 1: 30 i 2 2: 30 3 3: 30 4 4: 30 Time

Interval Partitioning • Interval partitioning. • Lecture j starts at sj and finishes at fj. • Goal: find minimum number of classrooms to schedule all lectures so that no two occur at the same time in the same room. • Ex: This schedule uses only 3. c 3 d b 2 a 1 9 9: 30 f j g i h e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 Time

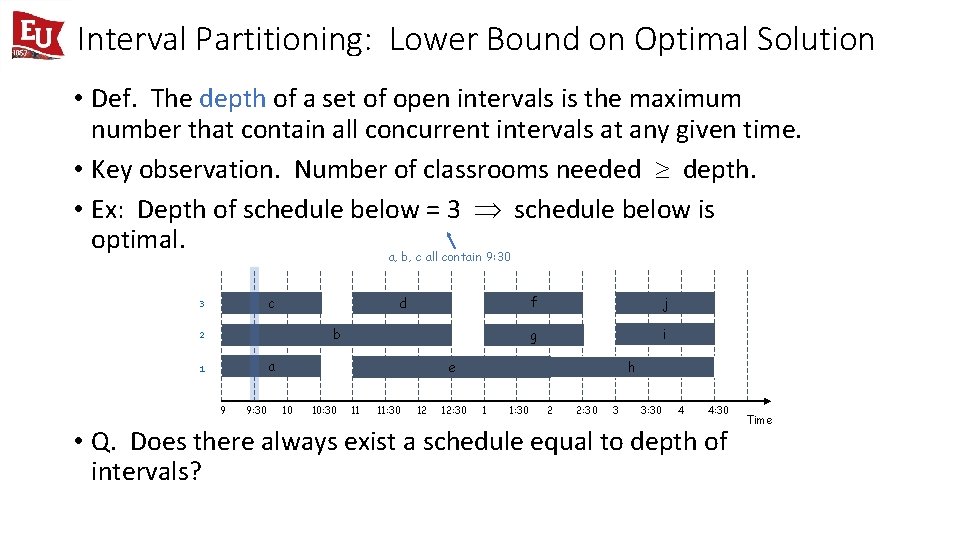
Interval Partitioning: Lower Bound on Optimal Solution • Def. The depth of a set of open intervals is the maximum number that contain all concurrent intervals at any given time. • Key observation. Number of classrooms needed depth. • Ex: Depth of schedule below = 3 schedule below is optimal. a, b, c all contain 9: 30 c 3 d b 2 a 1 9 9: 30 f j g i h e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 • Q. Does there always exist a schedule equal to depth of intervals? Time

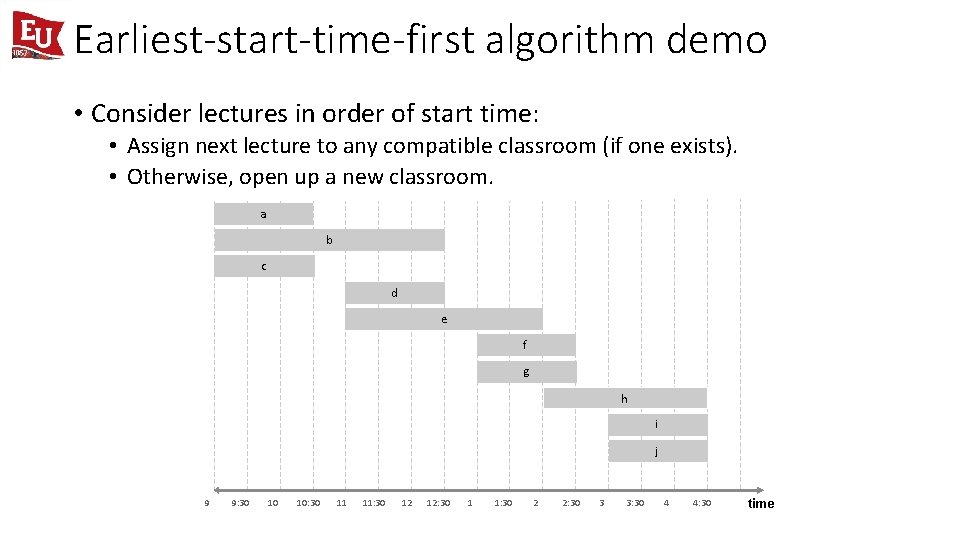
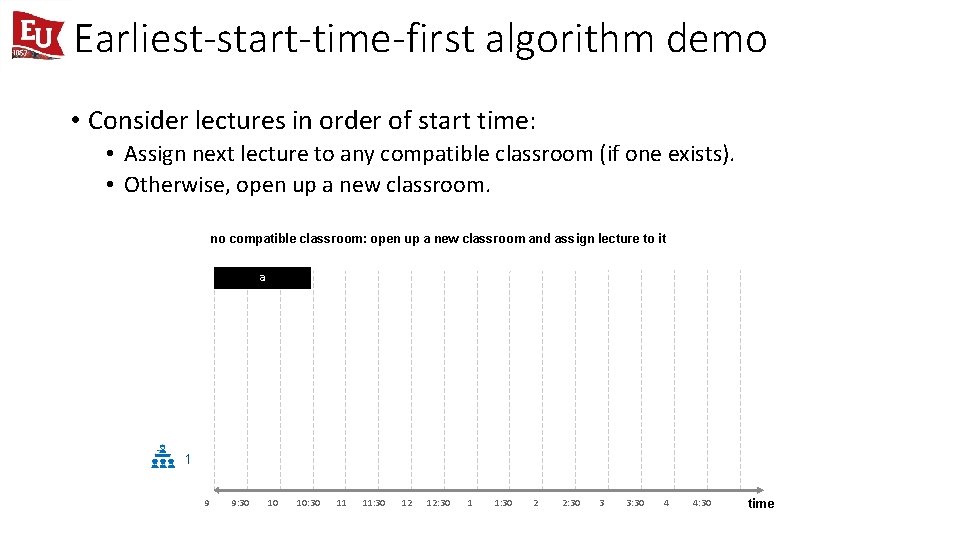
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. a b c d e f g h i j 9 9: 30 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. no compatible classroom: open up a new classroom and assign lecture to it a 1 9 9: 30 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

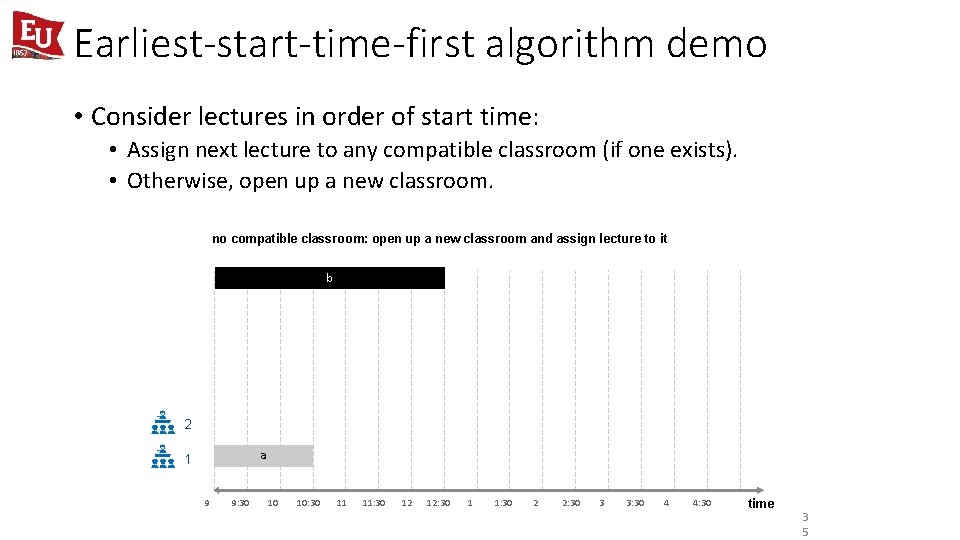
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. no compatible classroom: open up a new classroom and assign lecture to it b 2 a 1 9 9: 30 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time 3 5

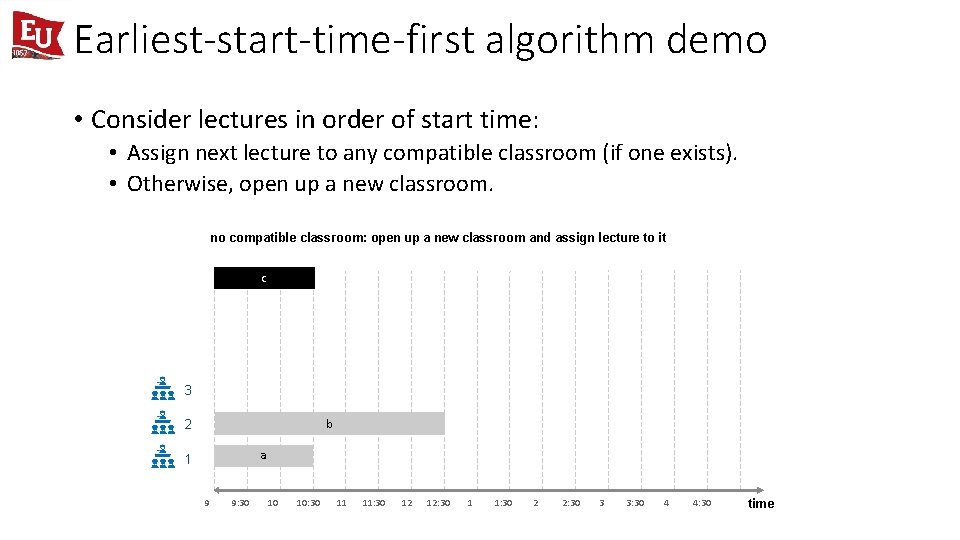
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. no compatible classroom: open up a new classroom and assign lecture to it c 3 b 2 a 1 9 9: 30 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

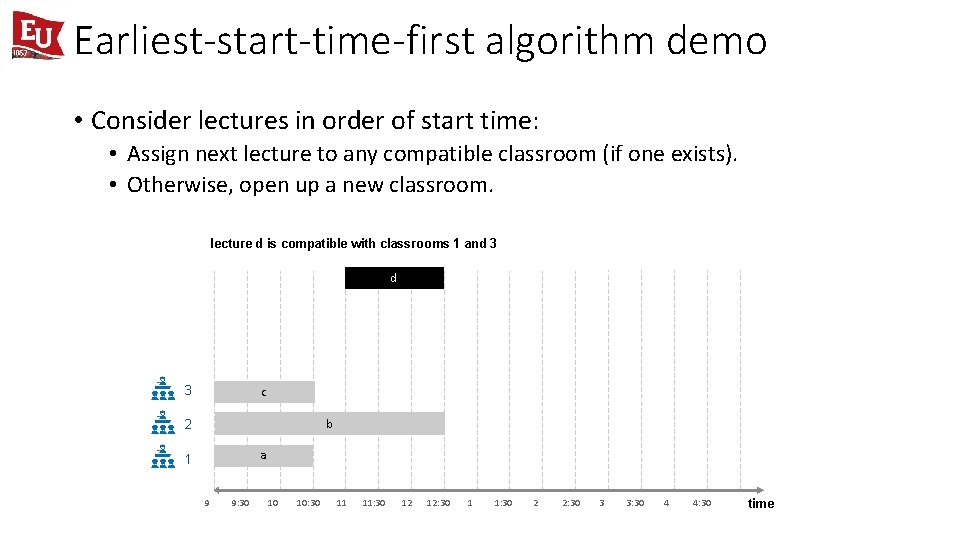
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. lecture d is compatible with classrooms 1 and 3 c b 2 a 1 9 9: 30 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

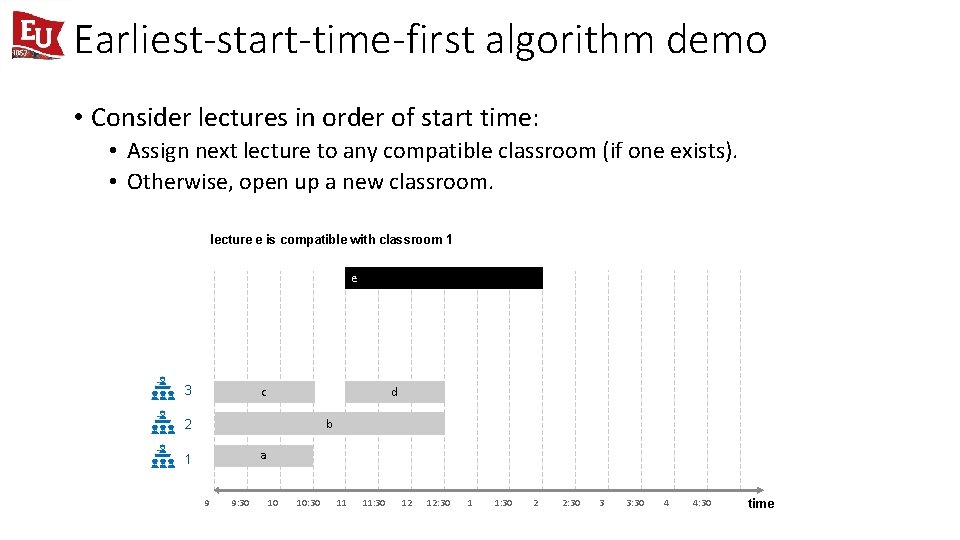
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. lecture e is compatible with classroom 1 e 3 c d b 2 a 1 9 9: 30 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

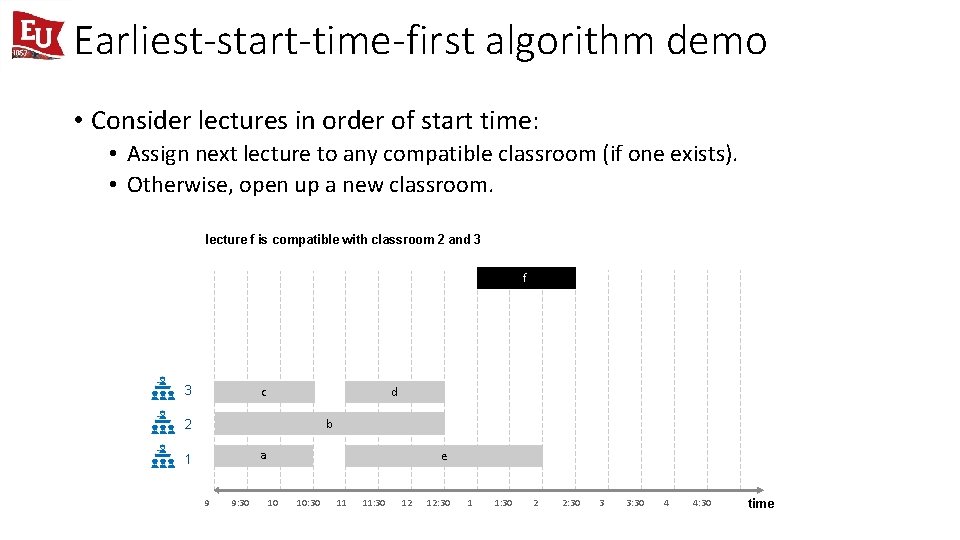
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. lecture f is compatible with classroom 2 and 3 f 3 c d b 2 a 1 9 9: 30 e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

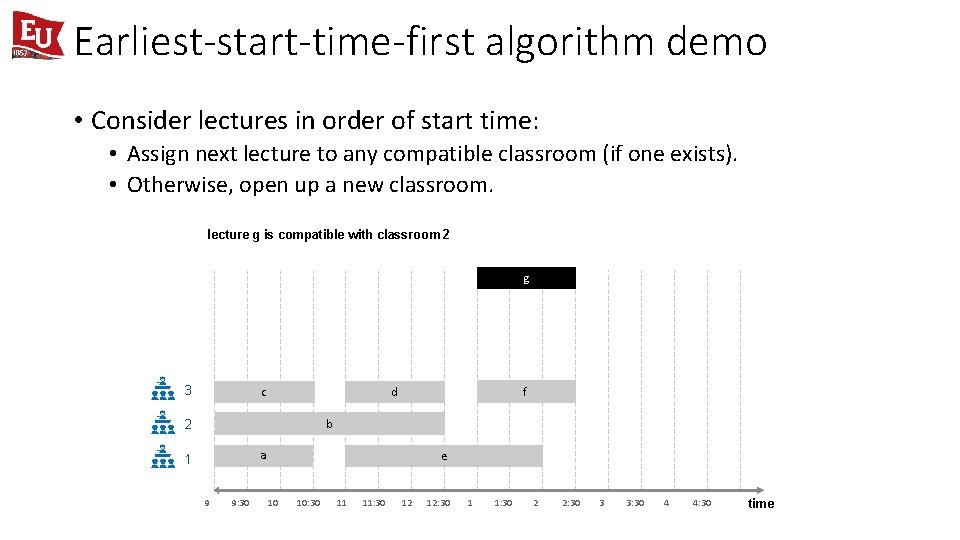
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. lecture g is compatible with classroom 2 g 3 c f d b 2 a 1 9 9: 30 e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

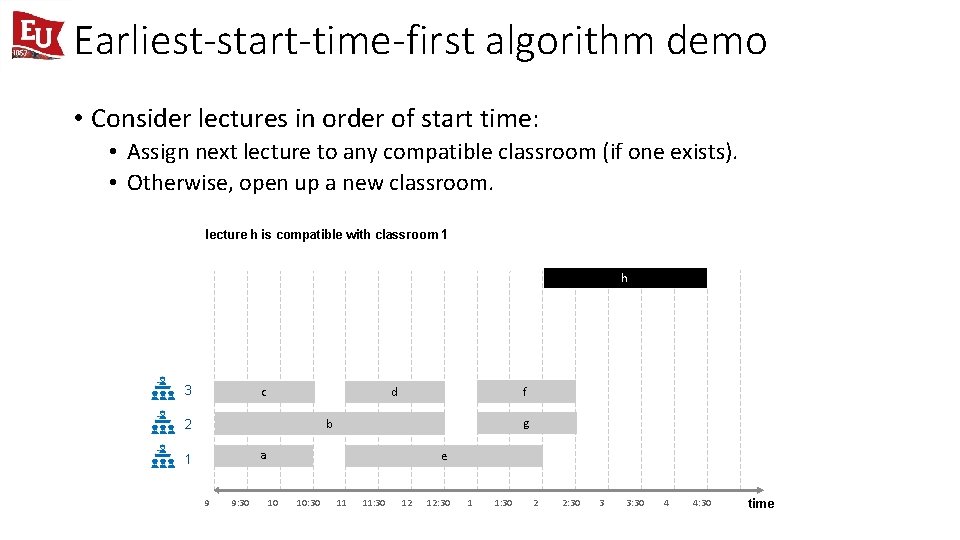
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. lecture h is compatible with classroom 1 h 3 c f d g b 2 a 1 9 9: 30 e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

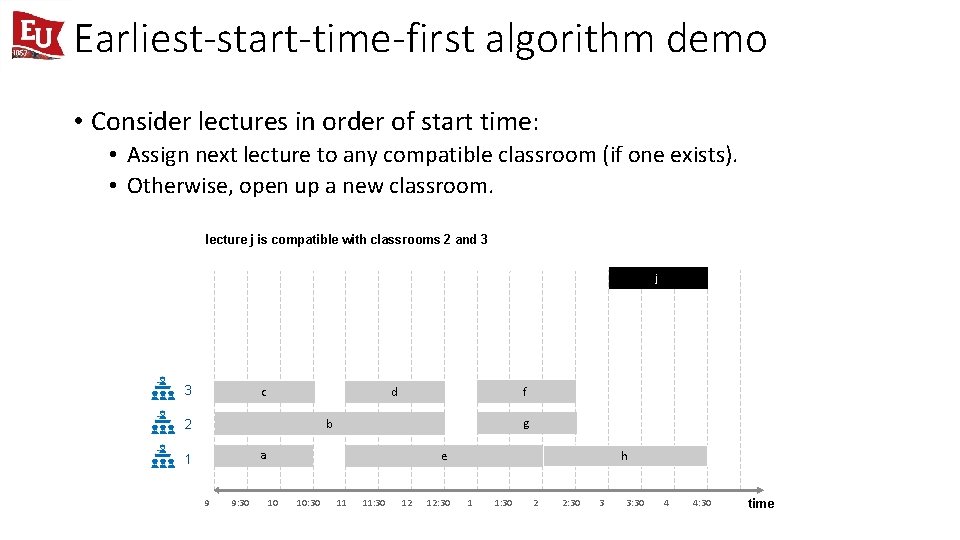
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. lecture j is compatible with classrooms 2 and 3 j 3 c f d g b 2 a 1 9 9: 30 h e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

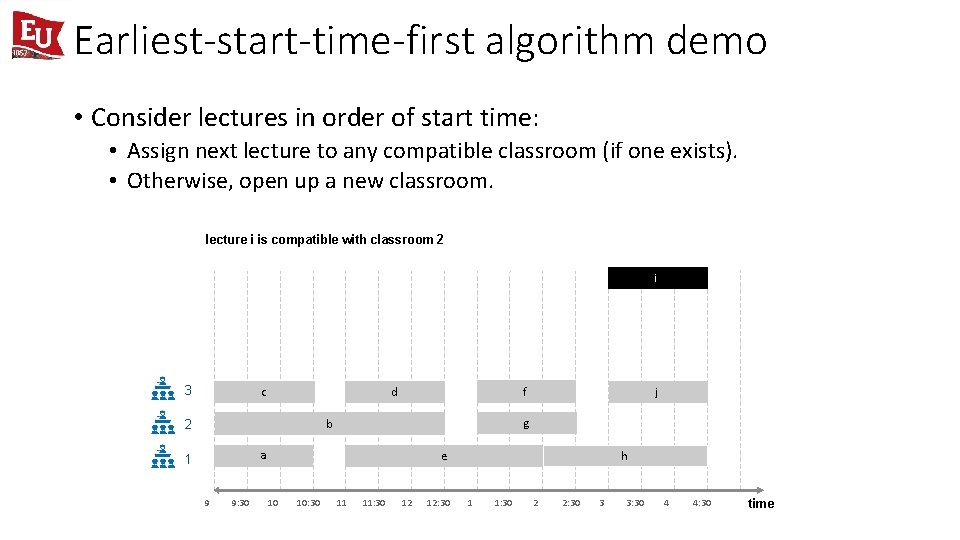
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. lecture i is compatible with classroom 2 i 3 c f d g b 2 a 1 9 9: 30 j h e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

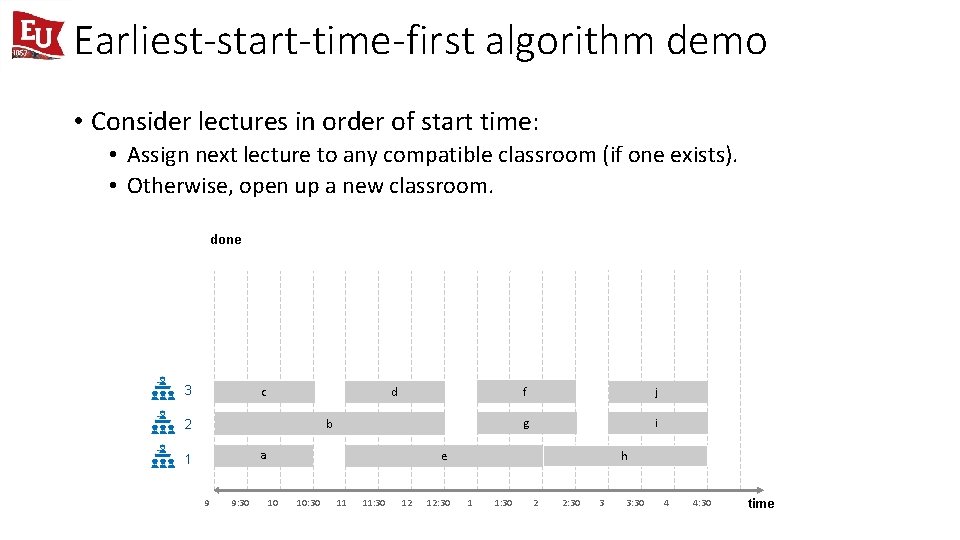
Earliest-start-time-first algorithm demo • Consider lectures in order of start time: • Assign next lecture to any compatible classroom (if one exists). • Otherwise, open up a new classroom. done 3 c d b 2 a 1 9 9: 30 f j g i h e 10 10: 30 11 11: 30 12 12: 30 1 1: 30 2 2: 30 3 3: 30 4 4: 30 time

Interval Partitioning: Greedy Algorithm • Greedy algorithm. Consider lectures in increasing order of start time: assign lecture to any compatible classroom. Sort intervals by starting time so that s 1 s 2 . . . sn. d 0 number of allocated classrooms for j = 1 to n if (lecture schedule else allocate schedule d d + } { j is compatible with some classroom k) lecture j in classroom k a new classroom d + 1 lecture j in classroom d + 1 1 • Implementation. O(n log n).