Great Theoretical Ideas In Computer Science Quiz Review
































![A Finite Continued Fraction Denoted by [2, 3, 4, 2, 0, 0, 0, …] A Finite Continued Fraction Denoted by [2, 3, 4, 2, 0, 0, 0, …]](https://slidetodoc.com/presentation_image_h2/f3f98242c922ed1eb7fc32906cf1c37f/image-35.jpg)
![An Infinite Continued Fraction Denoted by [1, 2, 2, 2, …] An Infinite Continued Fraction Denoted by [1, 2, 2, 2, …]](https://slidetodoc.com/presentation_image_h2/f3f98242c922ed1eb7fc32906cf1c37f/image-36.jpg)







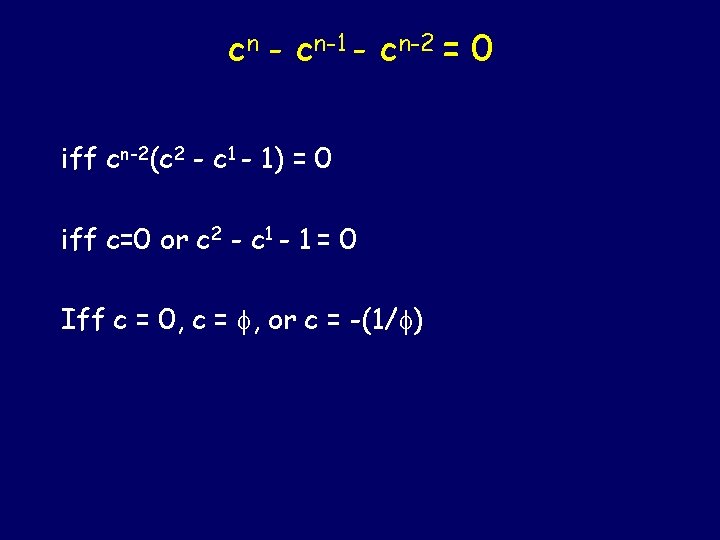










- Slides: 55

Great Theoretical Ideas In Computer Science Quiz Review CS 15 -251 March 17, 2005 Carnegie Mellon University Review for Quiz 2 Spring 2005

Starring Bonzo Jr… Starring (251 student) and Lucky (the turtle who introduced the magic square)

Disclaimer This set of lecture slides is intended as an OVERVIEW of the things you should know; it is insufficient to simply glance over these slides 10 minutes before the quiz. Moreover, this quiz review is NOT a substitute for the lectures; if you missed any lecture, watching the video is highly recommended.

Administrative Stuff First, a quick review of the administrative stuff. – 50 minutes long – Divided into 4 conceptual sections – Practice quizzes have been/will be uploaded.

Section 1: Repeat After me This section contains about 6 -8 questions based on quick facts covered in lecture. If you went to each lecture and paid attention, you should be fine. It is recommended that you skim over the lecture notes before the quiz to refresh your memory on the subject matter. Yay! Free points just for going to lecture and skimming over the notes

Section 2: Reading Solutions You are expected to read the given solutions to all homework and recitation problems - this section is comprised of one or two questions that are literally identical to questions that we've given you before. Note that the problems we ask can come from any previous assignment. (its even possible that we'll ask for the same problem's solution on all three quizzes).

Section 3: Basic Techniques These problems are based on techniques taught during class, and practiced in HWs/recitations. If you practice the ideas taught in lecture, you should have very little trouble with this section (problems vary only slightly from results derived in lecture). HINT: Look at the stuff from Monday’s recitation and the practice quizzes.

Section 4: A Moment’s Thought These problems are similar to problems given on homework assignments, albeit easier. If you do well on homework assignments, you shouldn't have too much trouble with this section. Who named this section…?

Time management Don’t forget about time management! The first two sections are designed to be able to be completed relatively quickly - don’t spend all your time on a Repeat After Me question that is worth only 5 points!

Beginning of Material Review Enough; I know all this! What’s going to be on the quiz?

Stuff quiz The new material foron Quiz 2 is from Lecture 9: Counting III to Lecture 17: On Time and Input Size. We are assuming that you already have an understanding of the material from lectures 1 -8. While we won’t explicitly test on that, you may need the knowledge you’ve learned from those lectures in answering the questions.

Key Areas The following areas are rated as very likely to appear on your quiz. – – – Finite State Machines (DFAs). Counting and Binomials. Matchings (including the TMA). GCDs and Continued Fractions Fibonacci and Fibonacci-like series. Asymptotic notation and runtime analysis.

Table of contents – – – Finite State Machines (DFAs). Counting and Binomials. Matchings (including the TMA). GCDs and Continued Fractions Fibonacci and Fibonacci-like series. Asymptotic notation and runtime analysis.

Finite Automaton – quick review Finite set of states A start state A set of accepting states A finite alphabet State transition instructions a b # x 1

Pumping Lemma In simple terms, the pumping lemma says that for any string that’s long enough, there’s a part of it we can repeat as many times as we want (or even delete, if we let i = 0), and still get a string that’s accepted.

Formal definition of pumping lemma The pumping lemma states that if there exists a DFA accepting a certain language, then there is a positive integer k (called the pumping length) so that any string s whose length is greater than or equal to k can be split up into three strings, u, v, and w, with certain properties: 1. v is not empty; 2. |uv| £ k, and 3. The string uviw is also accepted by the DFA.

Regular Expressions What strings are accepted by the following regexes? – – – Ø ε 1001 10*1 (0+10+111)* 1(0+1)*0(0+1)*1

Important Concepts Can you do the following? - Construct a DFA that accepts all strings with a length that is a multiple of 2 or 3. - Prove that the language of palindromes is not regular (use of pumping lemma is sufficient but not necessary). - Convert a simple regex to a DFA and vice versa?

Table of contents – – – Finite State Machines (DFAs). Counting and Binomials. Matchings (including the TMA). GCDs and Continued Fractions Fibonacci and Fibonacci-like series. Asymptotic notation and runtime analysis.

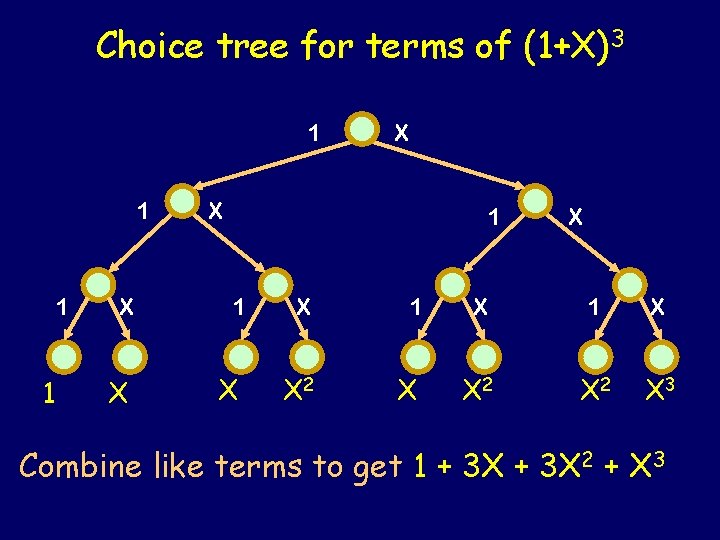
Choice tree for terms of (1+X)3 1 1 X X X 1 X X 2 X 2 X 3 Combine like terms to get 1 + 3 X 2 + X 3

The Binomial Formula Binomial Coefficients binomial expression

The Binomial Formula Be sure you can handle variants on this (remember the problem from Monday’s recitation)

Pascal’s Triangle 1 So very many properties… 1 1 1 2 3 4 5 6 1 3 6 10 15 1 1 4 10 20 1 5 15 1 6 1

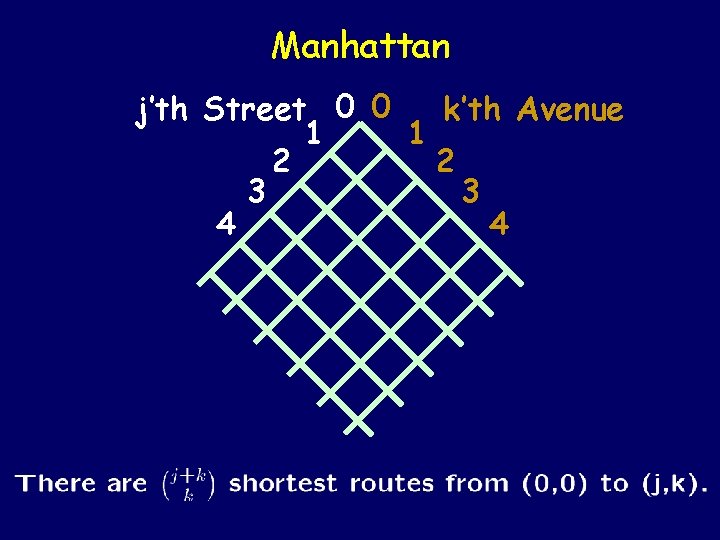
Manhattan j’th Street 0 0 k’th Avenue 1 1 2 2 3 3 4 4

Table of contents – – – Finite State Machines (DFAs). Counting and Binomials. Matchings (including the TMA). GCDs and Continued Fractions Fibonacci and Fibonacci-like series. Asymptotic notation and runtime analysis.

Rogue Couples Suppose we pair off all the boys and girls. Now suppose that some boy and some girl prefer each other to the people to whom they are paired. They will be called a rogue couple.

Stable Pairings A pairing of boys and girls is called stable if it contains no rogue couples. 3, 5, 2, 1, 4 3, 2, 5, 1, 4 1 1 5, 2, 1, 4, 3 1, 2, 5, 3, 4 2 2 4, 3, 5, 1, 2 4, 3, 2, 1, 5 3 3 1, 2, 3, 4, 5 1, 3, 4, 2, 5 4 4 2, 3, 4, 1, 5 1, 2, 4, 5, 3 5 5

Traditional Marriage Algorithm For each day that some boy gets a “No” do: • Morning – Each girl stands on her balcony – Each boy proposes under the balcony of the best girl whom he has not yet crossed off • Afternoon (for those girls with at least one suitor) – To today’s best suitor: “Maybe, come back tomorrow” – To any others: “No, I will never marry you” • Evening – Any rejected boy crosses the girl off his list Each girl marries the boy to whom she just said “maybe”

Opinion Poll ff o r e t t e l a b n s i o i s t o y i h W trad e bo in g, th ls? ir n i g t da r the o

Table of contents – – – Finite State Machines (DFAs). Counting and Binomials. Matchings (including the TMA). GCDs and Continued Fractions Fibonacci and Fibonacci-like series. Asymptotic notation and runtime analysis.

Euclid’s GCD Formula Euclid(A, B) // requires A B 0 If B=0 then return A else return Euclid(B, A mod B) Note: GCD(67, 29) = 1 Euclid(67, 29) Euclid(29, 9) Euclid(9, 2) Euclid(2, 1) Euclid(1, 0) outputs 1 67 mod 29 = 9 29 mod 9 = 2 9 mod 2 = 1 2 mod 1 = 0

Extended GCD Algorithm The lecture also covered Euclid’s Extended GCD Algorithm – that might be something you should take a look at.

The multiplicative inverse of x ≡ Zn* is the unique y є Zn* such that x *n y ≡ n 1. TO QUICKLY COMPUTE Y FROM X: Run Extended_Euclid(x, n). It returns a, b, and d such that ax+bn = d But d = GCD(x, n) = 1, so ax + bn = 1 Hence MODULO n: ax = 1 (mod n) Thus, a is the multiplicative inverse of x.

A (Simple) Continued Fraction Is Any Expression Of The Form: where a, b, c, … are whole numbers.
![A Finite Continued Fraction Denoted by 2 3 4 2 0 0 0 A Finite Continued Fraction Denoted by [2, 3, 4, 2, 0, 0, 0, …]](https://slidetodoc.com/presentation_image_h2/f3f98242c922ed1eb7fc32906cf1c37f/image-35.jpg)
A Finite Continued Fraction Denoted by [2, 3, 4, 2, 0, 0, 0, …]
![An Infinite Continued Fraction Denoted by 1 2 2 2 An Infinite Continued Fraction Denoted by [1, 2, 2, 2, …]](https://slidetodoc.com/presentation_image_h2/f3f98242c922ed1eb7fc32906cf1c37f/image-36.jpg)
An Infinite Continued Fraction Denoted by [1, 2, 2, 2, …]

An infinite continued fraction

Phi! Φ

Table of contents – – – Finite State Machines (DFAs). Counting and Binomials. Matchings (including the TMA). GCDs and Continued Fractions Fibonacci and Fibonacci-like series. Asymptotic notation and runtime analysis.

Check HW/Recitation The best way to review for this particular section is to look over the Fibonacci homework. Also, the recitation problems from Monday on Fibonacci are EXCELLENT practice.

Beginning of Material Review How did we get the closed form for Fibonacci-like series?

A technique to derive the formula for the Fibonacci numbers Fn is defined by two conditions: Base condition: F 0=0, F 1=1 Inductive condition: Fn=Fn-1+Fn-2

Forget the base condition and concentrate on satisfying the inductive condition Inductive condition: Fn=Fn-1+Fn-2 Consider solutions of the form: Fn= cn for some complex constant c C must satisfy: cn - cn-1 - cn-2 = 0
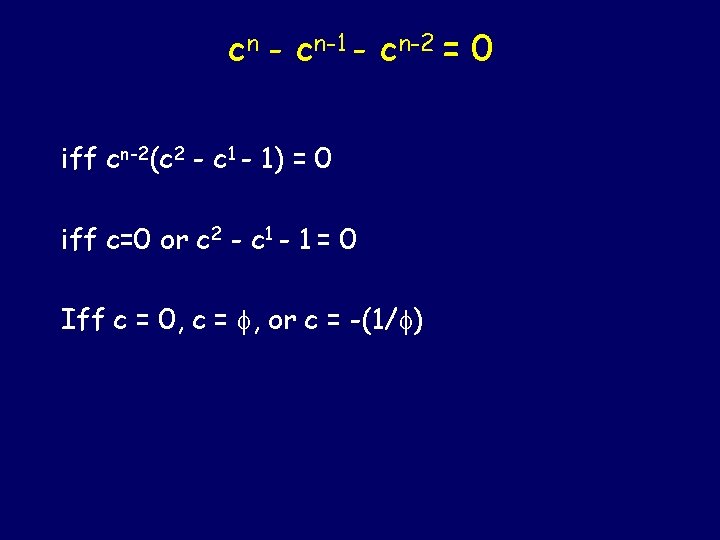
cn - cn-1 - cn-2 = 0 iff cn-2(c 2 - c 1 - 1) = 0 iff c=0 or c 2 - c 1 - 1 = 0 Iff c = 0, c = , or c = -(1/ )

c = 0, c = , or c = -(1/ ) So for all these values of c the inductive condition is satisfied: cn - cn-1 - cn-2 = 0 Do any of them happen to satisfy the base condition as well? c 0=0 and c 1=1? ROTTEN LUCK

Insight: if 2 functions g(n) and h(n) satisfy the inductive condition then so does a g(n) + b h(n) for all complex a and b g(n)-g(n-1)-g(n-2)=0 ag(n)-ag(n-1)-ag(n-2)=0 h(n)-h(n-1)-h(n-2)=0 bh(n)-bh(n-1)-bh(n-2)=0 (a g(n) + b h(n)) + (a g(n-1) + b h(n-1)) + (a g(n-2) + b h(n-2)) = 0

a, b a n + b (-1/ )n satisfies the inductive condition Set a and b to fit the base conditions. n=0 : n=1 : a+b=0 a 1 + b (-1/ )1 = 1 Two equalities in two unknowns (a and b). Now solve for a and b: this gives a = 1/ 5 b = -1/ 5

Table of contents – – – Finite State Machines (DFAs). Counting and Binomials. Matchings (including the TMA). GCDs and Continued Fractions Fibonacci and Fibonacci-like series. Asymptotic notation and runtime analysis.

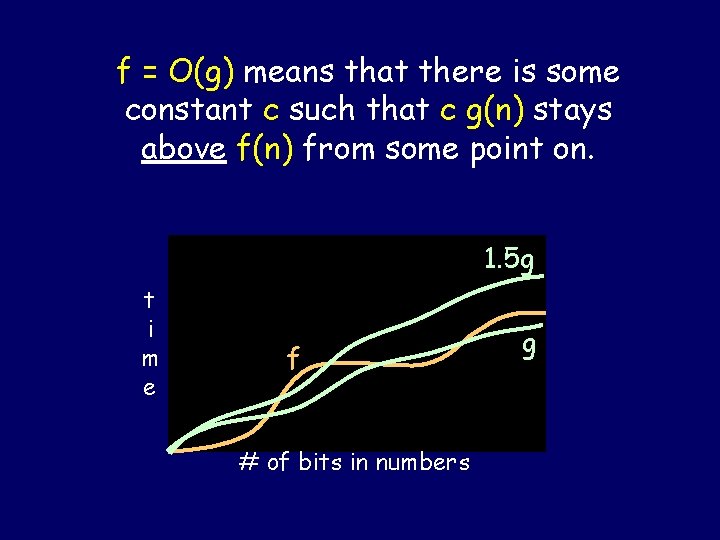
Useful notation to discuss growth rates For any two monotonic functions f and g from the positive integers to the positive integers, we say “f = O(g)” or “f is O(g)” if Some constant times g eventually dominates f [Formally: there exists a constant c such that for all sufficiently large n: f(n) ≤ c g(n) ]

O(n)that graph f = O(g) means there is some constant c such that c g(n) stays above f(n) from some point on. 1. 5 g t i m e f # of bits in numbers g

More useful notation: Ω For any two monotonic functions f and g from the positive integers to the positive integers, we say if: “f = Ω(g)” or “f is Ω(g)” f eventually dominates some constant times g [Formally: there exists a constant c such that for all sufficiently large n: f(n) ≥ c g(n) ]

Yet more useful notation: Θ For any two monotonic functions f and g from the positive integers to the positive integers, we say “f = Θ(g)” or “f is Θ(g)” if: f = O(g) and f = Ω(g)


Final Thoughts Do the practice quizzes (or at least look over them). Don’t forget that the processor lab is due on Tuesday at the beginning of class; make sure to schedule everything appropriately. Good luck!

Fin