Great Ideas in Computer Architecture Machine Structures Caches

Great Ideas in Computer Architecture (Machine Structures) Caches Part 3 Instructors: Yuanqing Cheng http: //www. cadetlab. cn/sp 18. html 10/28/2021 Spring 2018 - Lecture #16 1

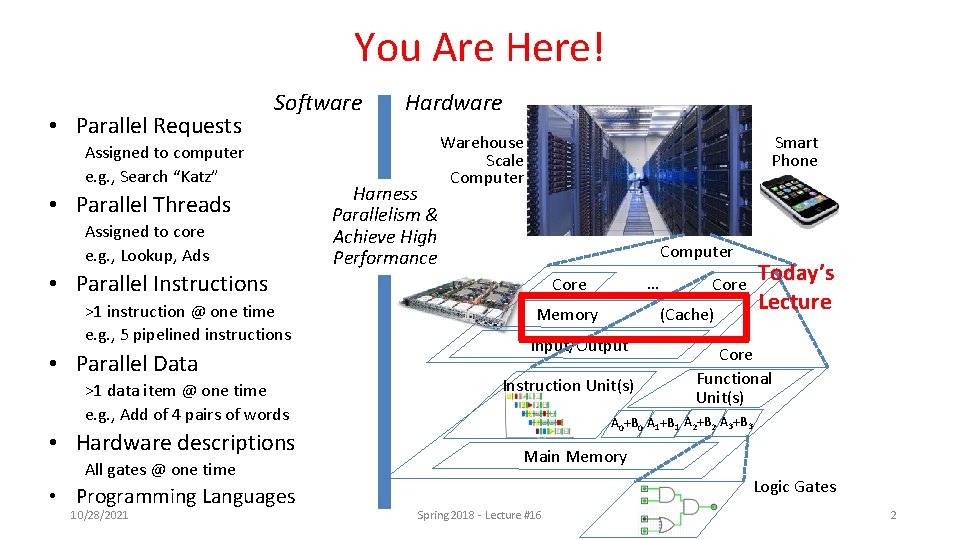
You Are Here! • Parallel Requests Software Assigned to computer e. g. , Search “Katz” • Parallel Threads Assigned to core e. g. , Lookup, Ads • Parallel Instructions >1 instruction @ one time e. g. , 5 pipelined instructions • Parallel Data >1 data item @ one time e. g. , Add of 4 pairs of words • Hardware descriptions All gates @ one time • Programming Languages 10/28/2021 Hardware Harness Parallelism & Achieve High Performance Smart Phone Warehouse Scale Computer … Core Memory Core (Cache) Input/Output Instruction Unit(s) Today’s Lecture Core Functional Unit(s) A 0+B 0 A 1+B 1 A 2+B 2 A 3+B 3 Main Memory Logic Gates Spring 2018 - Lecture #16 2

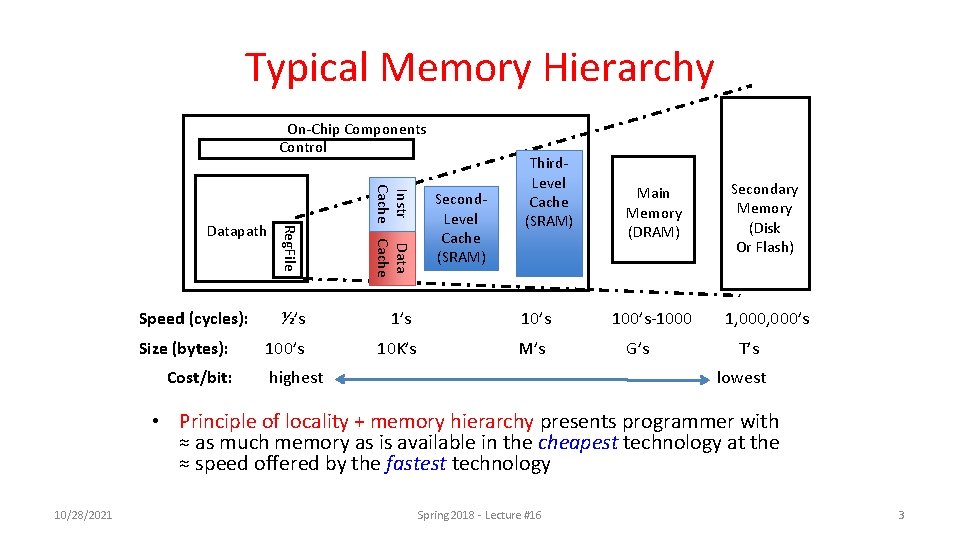
Typical Memory Hierarchy On-Chip Components Control Reg. File Instr Data Cache ½’s 10’s 10 K’s M’s Datapath Speed (cycles): Size (bytes): Cost/bit: Third. Level Cache (SRAM) Second. Level Cache (SRAM) highest Main Memory (DRAM) Secondary Memory (Disk Or Flash) 100’s-1000 1, 000’s G’s T’s lowest • Principle of locality + memory hierarchy presents programmer with ≈ as much memory as is available in the cheapest technology at the ≈ speed offered by the fastest technology 10/28/2021 Spring 2018 - Lecture #16 3

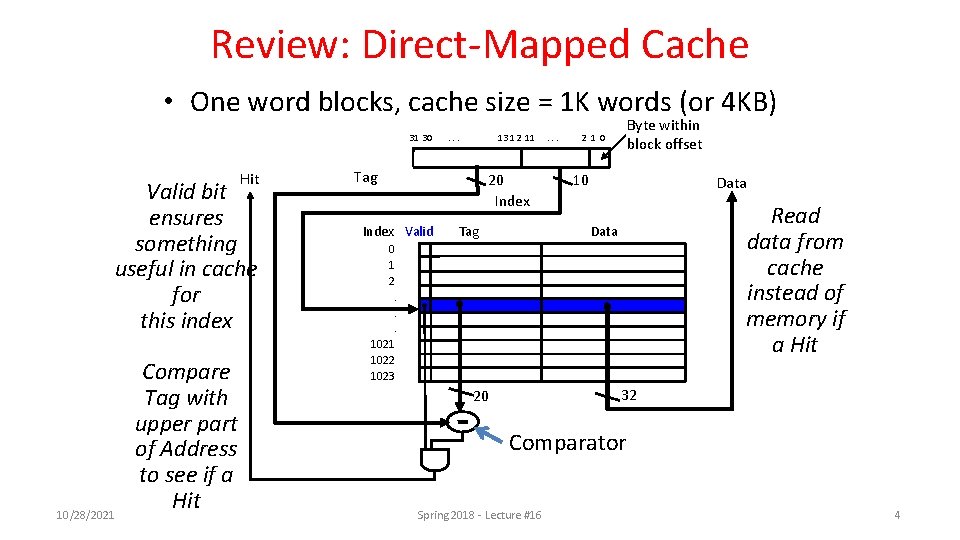
Review: Direct-Mapped Cache • One word blocks, cache size = 1 K words (or 4 KB) 31 30 Hit Valid bit ensures something useful in cache for this index 10/28/2021 Compare Tag with upper part of Address to see if a Hit . . . 13 12 11 Tag 20 Index Valid Tag . . . Byte within block offset 2 1 0 10 Data Read data from cache instead of memory if a Hit Data 0 1 2. . . 1021 1022 1023 32 20 Comparator Spring 2018 - Lecture #16 4

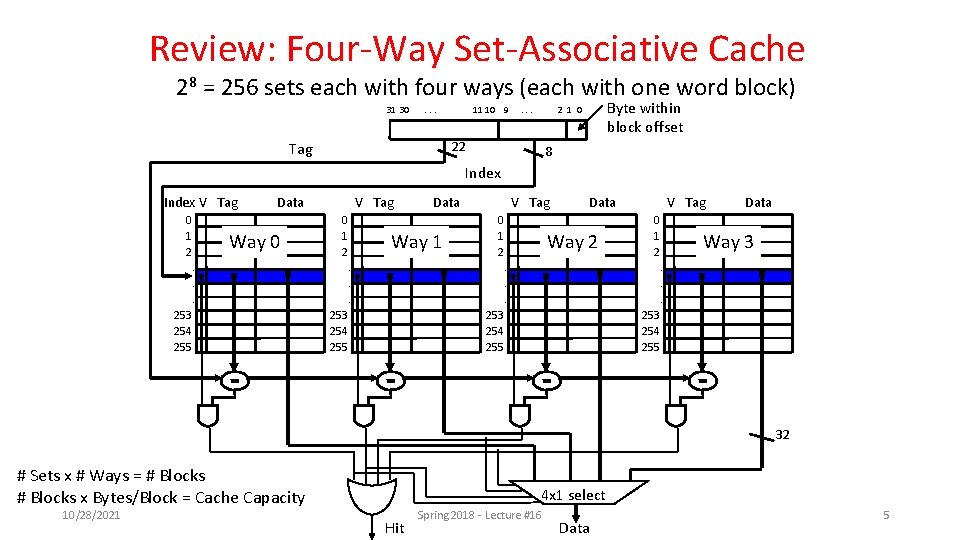
Review: Four-Way Set-Associative Cache 28 = 256 sets each with four ways (each with one word block) 31 30 . . . 11 10 9 . . . 22 Tag Byte within block offset 2 1 0 8 Index V Tag 0 1 2 V Tag Data Way 0 0 1 2 . . . 253 254 255 V Tag Data Way 1 0 1 2 . . . V Tag Data Way 2 0 1 2 . . . 253 254 255 Data Way 3. . . 253 254 255 32 # Sets x # Ways = # Blocks x Bytes/Block = Cache Capacity 10/28/2021 4 x 1 select Hit Spring 2018 - Lecture #16 Data 5

Review: Range of Set-Associative Caches • For a fixed-size cache and fixed block size, each increase by a factor of two in associativity doubles the number of blocks per set (i. e. , the number or ways) and halves the number of sets – decreases the size of the index by 1 bit and increases the size of the tag by 1 bit Used for tag compare Tag Decreasing associativity, less ways, more sets Selects the set Index 10/28/2021 Word offset Byte offset Increasing associativity, more ways, less sets Fully associative (only one set) Tag is all the bits except word and byte offset Direct mapped (only one way) Smaller tags, only a single comparator # Sets x # Ways = # Blocks x Bytes/Block = Cache Capacity Selects the word in the block Spring 2018 - Lecture #15 6

Review: Costs of Set-Associative Caches • N-way set-associative cache costs – N comparators (delay and area) – MUX delay (set selection) before data is available – Data available after set selection (and Hit/Miss decision). DM $: block is available before the Hit/Miss decision • In Set-Associative, not possible to just assume a hit and continue and recover later if it was a miss • When miss occurs, which way’s block selected for replacement? – Least Recently Used (LRU): one that has been unused the longest (principle of temporal locality) • Must track when each way’s block was used relative to other blocks in the set • For 2 -way SA $, one bit per set → set to 1 when a block is referenced; reset the other way’s bit (i. e. , “last used”) 10/28/2021 Spring 2018 - Lecture #16 7

Review: Cache Replacement Policies • Random Replacement – Hardware randomly selects a cache block for eviction • Least-Recently Used – Hardware keeps track of access history – Replace the entry that has not been used for the longest time – For 2 -way set-associative cache, need one bit for LRU replacement • Example of a Simple “Pseudo” LRU Implementation – Assume 64 Fully Associative entries – Hardware replacement pointer points to one cache entry – Whenever access is made to the entry the pointer points to: • Move the pointer to the next entry – Otherwise: do not move the pointer – (example of “not-most-recently used” replacement policy) 10/28/2021 Spring 2018 - Lecture #16 Entry 0 Replacement Pointer Entry 1 : Entry 63 8

Review: Write Policy Choices • Cache Hit: – Write through: writes both cache & memory on every access • Generally higher memory traffic but simpler pipeline & cache design – Write back: writes cache only, memory written only when dirty entry evicted • A dirty bit per line reduces write-back traffic • Must handle 0, 1, or 2 accesses to memory for each load/store • Cache Miss: – No write allocate: only write to main memory – Write allocate (aka fetch on write): fetch into cache • Common combinations: – Write through and no write allocate – Write back with write allocate 10/28/2021 Spring 2018 - Lecture #16 9

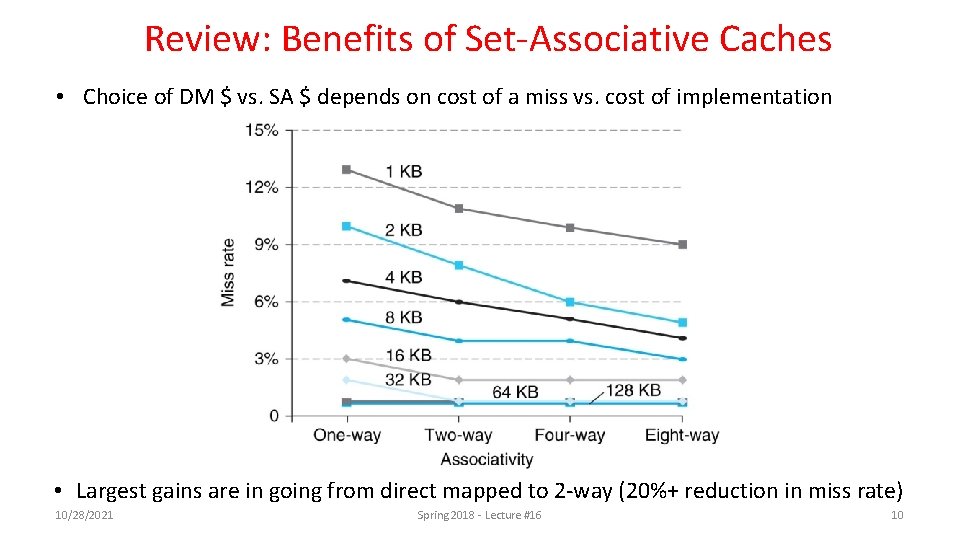
Review: Benefits of Set-Associative Caches • Choice of DM $ vs. SA $ depends on cost of a miss vs. cost of implementation • Largest gains are in going from direct mapped to 2 -way (20%+ reduction in miss rate) 10/28/2021 Spring 2018 - Lecture #16 10

Review: Average Memory Access Time (AMAT) • Average Memory Access Time (AMAT) is the average time to access memory considering both hits and misses in the cache AMAT = Time for a hit + Miss rate × Miss penalty Important Equation! 10/28/2021 Spring 2018 - Lecture #16 11

Outline • • • Understanding Cache Misses Increasing Cache Performance of multi-level Caches (L 1, L 2, …) Real world example caches And in Conclusion … 10/28/2021 Spring 2018 – Lecture #16 12

Outline • • • Understanding Cache Misses Increasing Cache Performance of multi-level Caches (L 1, L 2, …) Real world example caches And in Conclusion … 10/28/2021 Spring 2018 – Lecture #16 13

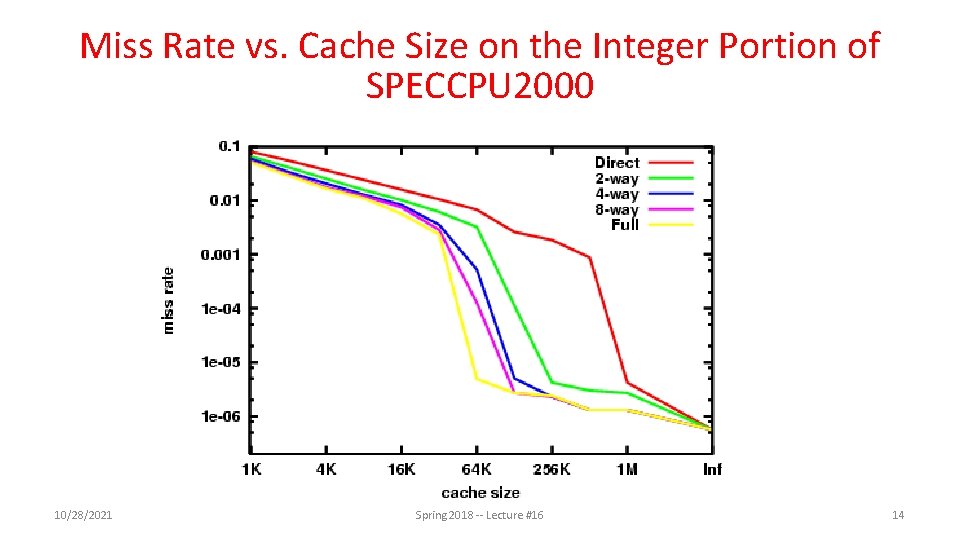
Miss Rate vs. Cache Size on the Integer Portion of SPECCPU 2000 10/28/2021 Spring 2018 -- Lecture #16 14

Sources of Cache Misses (3 C’s) • Compulsory (cold start, first reference): – 1 st access to a block, not a lot you can do about it • If running billions of instructions, compulsory misses are insignificant • Capacity: – Cache cannot contain all blocks accessed by the program • Misses that would not occur with infinite cache • Conflict (collision): – Multiple memory locations mapped to same cache set • Misses that would not occur with ideal fully associative cache 10/28/2021 Spring 2018 - Lecture #16 15

How to Calculate 3 C’s Using Cache Simulator 1. Compulsory: set cache size to infinity and fully associative, and count number of misses 2. Capacity: Change cache size from infinity, usually in powers of 2, and count misses for each reduction in size – 16 MB, 8 MB, 4 MB, … 128 KB, 64 KB, 16 KB 3. Conflict: Change from fully associative to n-way set associative while counting misses – Fully associative, 16 -way, 8 -way, 4 -way, 2 -way, 1 -way 10/28/2021 Spring 2018 - Lecture #16 16

3 Cs Analysis • Three sources of misses (SPEC 2000 integer and floating-point benchmarks) – Compulsory misses 0. 006%; not visible – Capacity misses, function of cache size – Conflict portion depends on associativity and cache size 10/28/2021 Spring 2018 - Lecture #16 17

Outline • • • Understanding Cache Misses Increasing Cache Performance of multi-level Caches (L 1, L 2, …) Real world example caches And in Conclusion … 10/28/2021 Spring 2018 – Lecture #16 18

Pipelined RISC-V RV 32 I Datapath (with I, D$) Recalculate PC+4 in M stage to avoid sending both PC and PC+4 down pipeline pc. F pc. D +4 pc. F+4 0 Addr. D IMEM Addr. A “Bubble” Primary I$ Addr Instr pc. F Reg[] Data. D Data. A alu. X 1 Hit? PCen Refill $ Data from Lower Levels of Memory Hierarchy 10/28/2021 inst. D pc. M pc. X Addr. B Data. B rs 1 X ALU inst. X Imm. DMEM alu. M Addr Branch Comp. rs 2 X +4 Data. R Data. W imm. X rs 2 M inst. M To Memory Controller Must pipeline instruction along with data, so control operates correctly in each stage Spring 2018 - Lecture #16 Primary D$ Addr Data. R Data. W Hit? inst Refill D$ data from Lower Levels of Memory Hierarchy Memory Controller W & Stall entire CPU on D$ miss Write Back/Thru to Memory 19

Improving Cache Performance AMAT = Time for a hit + Miss rate x Miss penalty • Reduce the time to hit in the cache – E. g. , Smaller cache • Reduce the miss rate – E. g. , Bigger cache • Reduce the miss penalty – E. g. , Use multiple cache levels 10/28/2021 Spring 2018 - Lecture #16 20

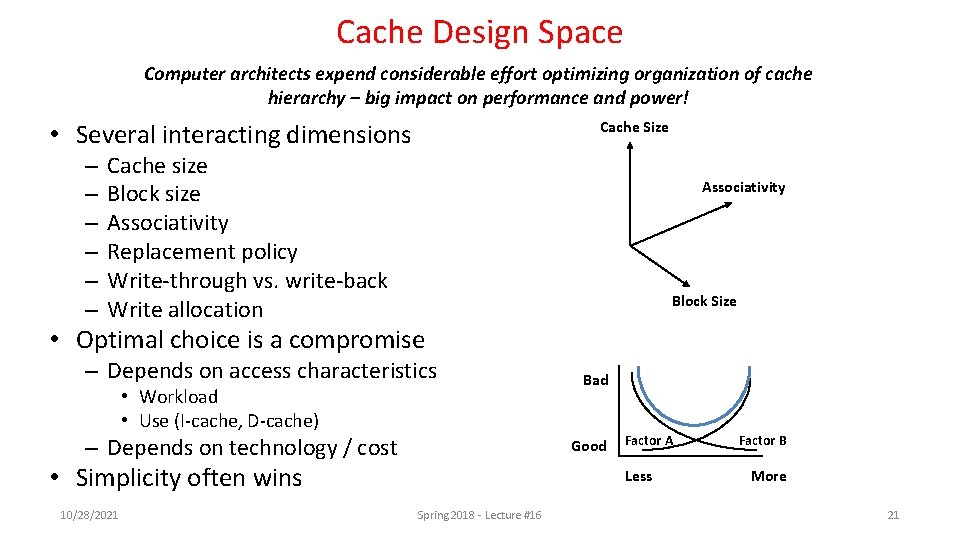
Cache Design Space Computer architects expend considerable effort optimizing organization of cache hierarchy – big impact on performance and power! Cache Size • Several interacting dimensions – – – Cache size Block size Associativity Replacement policy Write-through vs. write-back Write allocation Associativity Block Size • Optimal choice is a compromise – Depends on access characteristics • Workload • Use (I-cache, D-cache) – Depends on technology / cost Good • Simplicity often wins 10/28/2021 Bad Factor A Less Spring 2018 - Lecture #16 Factor B More 21

Break! 10/28/2021 Spring 2018 - Lecture #16 22

Peer Instruction • For a cache with constant total capacity, if we increase the number of ways by a factor of two, which statement is false: A : The number of sets is halved B : The tag width decreases C : The block size stays the same D : The set index decreases 10/28/2021 Spring 2018 - Lecture #16 23

Peer Instruction • For a cache with constant total capacity, if we increase the number of ways by a factor of two, which statement is false: A : The number of sets is halved B : The tag width decreases C : The block size stays the same D : The set index decreases 10/28/2021 Spring 2018 - Lecture #16 24

Peer Instruction • For S sets, N ways, B blocks, which statements hold? (i) The cache has B tags (ii) The cache needs N comparators (iii) B = N x S (iv) Size of Set Index = Log 2(S) A : (i) only B : (i) and (ii) only C : (i), (iii) only D : All four statements are true 10/28/2021 Spring 2018 - Lecture #16 25

Peer Instruction • For S sets, N ways, B blocks, which statements hold? (i) The cache has B tags (ii) The cache needs N comparators (iii) B = N x S (iv) Size of Set Index = Log 2(S) A : (i) only B : (i) and (ii) only C : (i), (iii) only D : All four statements are true 10/28/2021 Spring 2018 - Lecture #16 26

Primary Cache Parameters • Block size – How many bytes of data in each cache entry? • Associativity – How many ways in each set? – Direct-mapped => Associativity = 1 – Set-associative => 1 < Associativity < #Entries – Fully associative => Associativity = #Entries • Capacity (bytes) = Total #Entries * Block size • #Entries = #Sets * Associativity 10/28/2021 Spring 2018 - Lecture #16 27

Impact of Larger Cache on AMAT? • 1) Reduces misses (what kind(s)? ) • 2) Longer Access time (Hit time): smaller is faster – Increase in hit time will likely add another stage to the pipeline • At some point, increase in hit time for a larger cache may overcome improvement in hit rate, yielding a decrease in performance • Computer architects expend considerable effort optimizing organization of cache hierarchy – big impact on performance and power! 10/28/2021 Spring 2018 - Lecture #16 28

Increasing Associativity? • Hit time as associativity increases? – Increases, with large step from direct-mapped to >=2 ways, as now need to mux correct way to processor – Smaller increases in hit time for further increases in associativity • Miss rate as associativity increases? – Goes down due to reduced conflict misses, but most gain is from 1 ->2 ->4 way with limited benefit from higher associativities • Miss penalty as associativity increases? – Unchanged, replacement policy runs in parallel with fetching missing line from memory 10/28/2021 Spring 2018 - Lecture #16 29

Increasing #Entries? • Hit time as #entries increases? – Increases, since reading tags and data from larger memory structures • Miss rate as #entries increases? – Goes down due to reduced capacity and conflict misses – Architects rule of thumb: miss rate drops ~2 x for every ~4 x increase in capacity (only a gross approximation) • Miss penalty as #entries increases? – Unchanged At some point, increase in hit time for a larger cache may overcome the improvement in hit rate, yielding a decrease in performance 10/28/2021 Spring 2018 - Lecture #16 30

Increasing Block Size? • Hit time as block size increases? – Hit time unchanged, but might be slight hit-time reduction as number of tags is reduced, so faster to access memory holding tags • Miss rate as block size increases? – Goes down at first due to spatial locality, then increases due to increased conflict misses due to fewer blocks in cache • Miss penalty as block size increases? – Rises with longer block size, but with fixed constant initial latency that is amortized over whole block 10/28/2021 Spring 2018 - Lecture #16 31

Administrivia • • Midterm #2 2 weeks away! Jun 4 th! Review Session: May 24 th Project 1 -2 due Jun 4 th 11: 59 pm Homework 3 due May 24 th 10/28/2021 Spring 2018 - Lecture #16 32

Peer Instruction For a cache of fixed capacity and blocksize, what is the impact of increasing associativity on AMAT: A : Increases hit time, decreases miss rate B : Decreases hit time, decreases miss rate C : Increases hit time, increases miss rate D : Decreases hit time, increases miss rate 10/28/2021 Spring 2018 - Lecture #16 33

Peer Instruction For a cache of fixed capacity and blocksize, what is the impact of increasing associativity on AMAT: A : Increases hit time, decreases miss rate B : Decreases hit time, decreases miss rate C : Increases hit time, increases miss rate D : Decreases hit time, increases miss rate 10/28/2021 Spring 2018 - Lecture #16 34

Peer Instruction Impact of Larger Blocks on AMAT: • For fixed total cache capacity and associativity, what is effect of larger blocks on each component of AMAT: A : Decrease B : Unchanged C : Increase Hit Time? Miss Rate? Miss Penalty? 10/28/2021 Spring 2018 - Lecture #16 35

Peer Instruction Impact of Larger Blocks on AMAT: • For fixed total cache capacity and associativity, what is effect of larger blocks on each component of AMAT: A : Decrease B : Unchanged C : Increase Shorter tags +, mux at edge Hit Time? C: Unchanged (but slight increase possible) Miss Rate? A: Decrease (spatial locality; conflict? ? ? ) Miss Penalty? C: Increase (longer time to load block) Write Allocation? It depends! 10/28/2021 Spring 2018 - Lecture #16 36

Peer Instruction Impact of Larger Blocks on Misses: • For fixed total cache capacity and associativity, what is effect of larger blocks on each component of miss: A : Decrease B : Unchanged C : Increase Compulsory? Capacity? Conflict? 10/28/2021 Spring 2018 - Lecture #16 37

Peer Instruction Impact of Larger Blocks on Misses: • For fixed total cache capacity and associativity, what is effect of larger blocks on each component of miss: A : Decrease B : Unchanged C : Increase Compulsory? A: Decrease (if good Spatial Locality) Capacity? B: Increase (smaller blocks fit better) Conflict? A: Increase (more ways better!) Less effect for large caches 10/28/2021 Spring 2018 - Lecture #16 38

How to Reduce Miss Penalty? • Could there be locality on misses from a cache? – Use multiple cache levels! – With Moore’s Law, more room on die for bigger L 1$ and for secondlevel L 2$ – And in some cases even an L 3$! • Mainframes have ~1 GB L 4 cache off-chip 10/28/2021 Spring 2018 - Lecture #16 39

Break! 10/28/2021 Spring 2018 - Lecture #16 40

Outline • • • Understanding Cache Misses Increasing Cache Performance of Multi-level Caches (L 1, L 2, …) Real world example caches And in Conclusion … 10/28/2021 Spring 2018 – Lecture #16 41

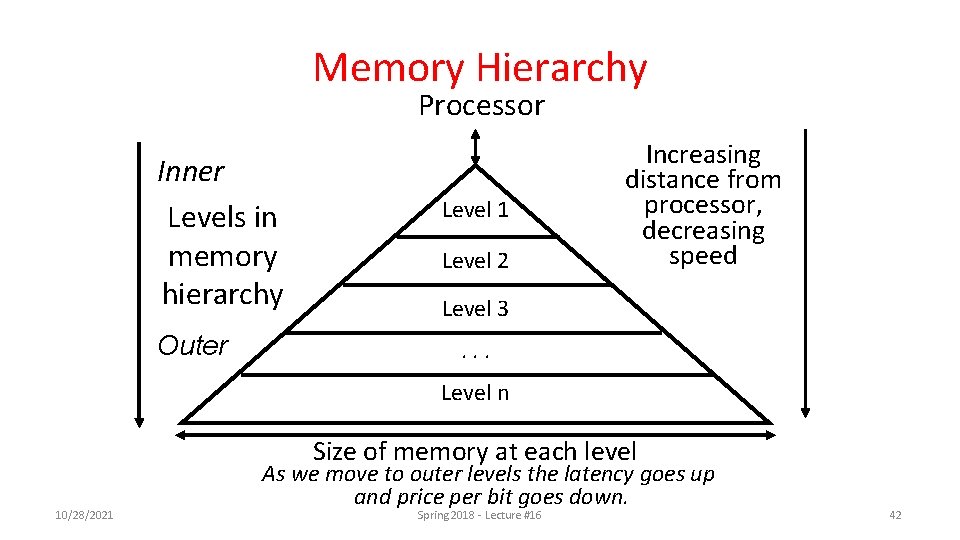
Memory Hierarchy Processor Inner Levels in memory hierarchy Outer Level 1 Level 2 Increasing distance from processor, decreasing speed Level 3. . . Level n Size of memory at each level 10/28/2021 As we move to outer levels the latency goes up and price per bit goes down. Spring 2018 - Lecture #16 42

Local vs. Global Miss Rates • Local miss rate: fraction of references to a given level of a cache that miss – Local Miss rate L 2$ = L 2$ Misses / L 1$ Misses = L 2$ Misses / total_L 2_accesses • Global miss rate: the fraction of references that miss in all levels of a multilevel cache and go all the way to memory – L 2$ local miss rate >> than the global miss rate 10/28/2021 Spring 2018 - Lecture #16 43

Local vs. Global Miss Rates • Local miss rate – the fraction of references to one level of a cache that miss – Local Miss rate L 2$ = $L 2 Misses / L 1$ Misses • Global miss rate – the fraction of references that miss in all levels of a multilevel cache – L 2$ local miss rate >> than the global miss rate • Global Miss rate = L 2$ Misses / Total Accesses = (L 2$ Misses / L 1$ Misses) × (L 1$ Misses / Total Accesses) = Local Miss rate L 2$ × Global Miss rate L 1$ • AMAT = Time for a hit + Miss rate × Miss penalty • AMAT = Time for a L 1$ hit + (local) Miss rate L 1$ × (Time for a L 2$ hit + (local) Miss rate L 2$ × L 2$ Miss penalty) 10/28/2021 Spring 2018 - Lecture #16 44

Multilevel Cache Considerations • Different design considerations for L 1$ and L 2$ – L 1$ focuses on fast access: minimize hit time to achieve shorter clock cycle, e. g. , smaller $ – L 2$, L 3$ focus on low miss rate: reduce penalty of long main memory access times: e. g. , Larger $ with larger block sizes/higher levels of associativity • Miss penalty of L 1$ is significantly reduced by presence of L 2$, so can be smaller/faster even with higher miss rate • For the L 2$, fast hit time is less important than low miss rate – L 2$ hit time determines L 1$’s miss penalty – L 2$ local miss rate >> than the global miss rate 10/28/2021 Spring 2018 -- Lecture #16 45

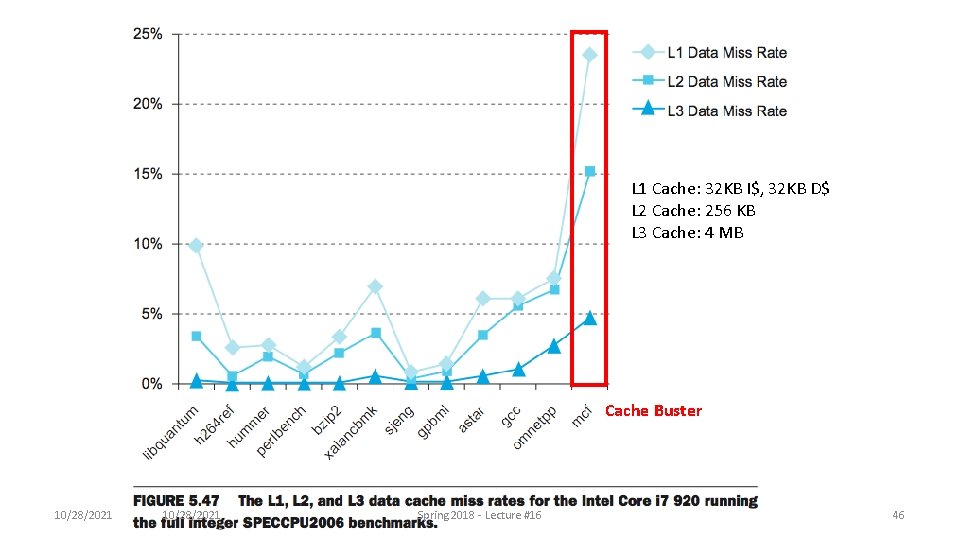
L 1 Cache: 32 KB I$, 32 KB D$ L 2 Cache: 256 KB L 3 Cache: 4 MB Cache Buster 10/28/2021 Spring Lecture #16 #13 Spring 2018 --- Lecture 46

Outline • • • Understanding Cache Misses Increasing Cache Performance of Multi-level Caches (L 1, L 2, …) Real world example caches And in Conclusion … 10/28/2021 Spring 2018 – Lecture #16 47

10/28/2021 Spring 2018 - Lecture #16 48

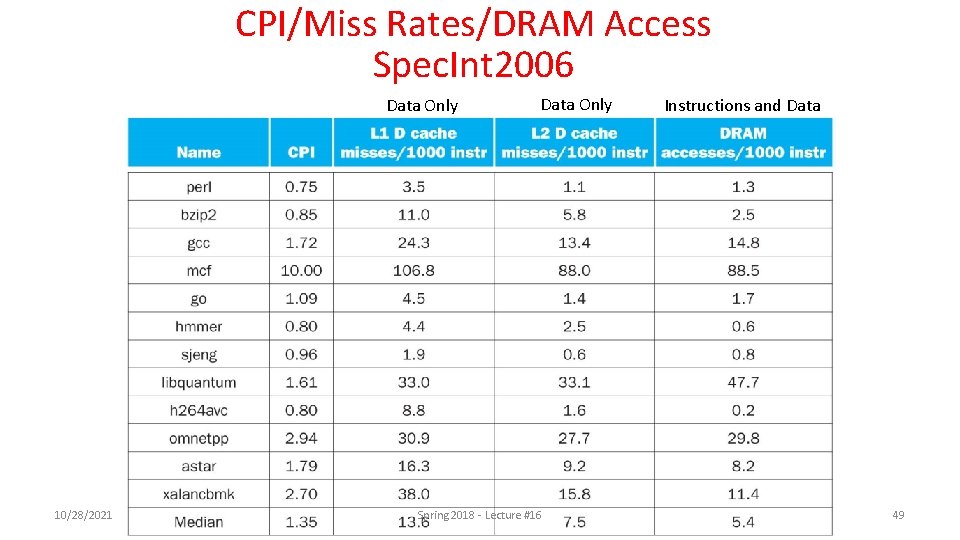
CPI/Miss Rates/DRAM Access Spec. Int 2006 Data Only 10/28/2021 Data Only Spring Lecture #16 #12 Spring 2018 --- Lecture Instructions and Data 49

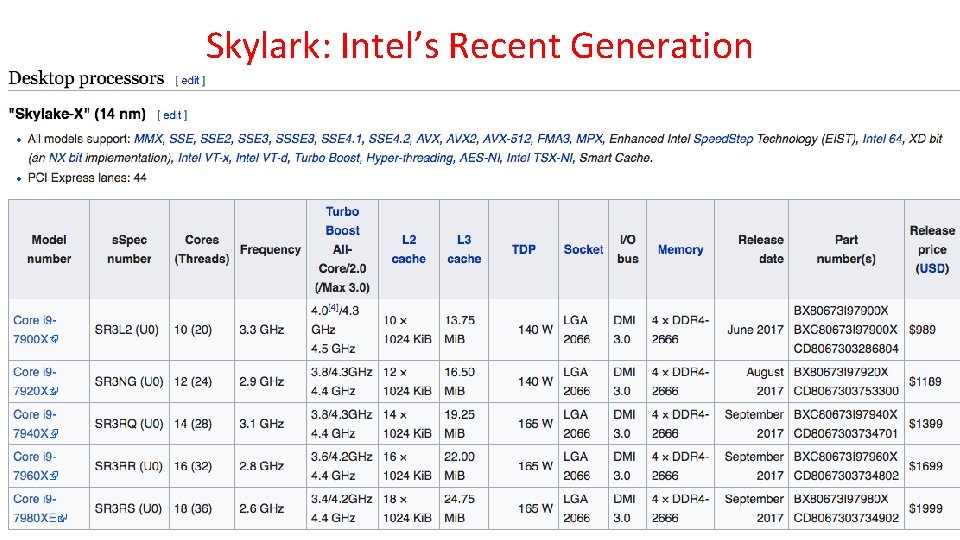
Skylark: Intel’s Recent Generation Laptop/Tablet Class CPUs 10/28/2021 Spring 2018 -- Lecture #16 50

Outline • • • Understanding Cache Misses Increasing Cache Performance of Multi-level Caches (L 1, L 2, …) Real world example caches And in Conclusion … 10/28/2021 Spring 2018 – Lecture #16 51

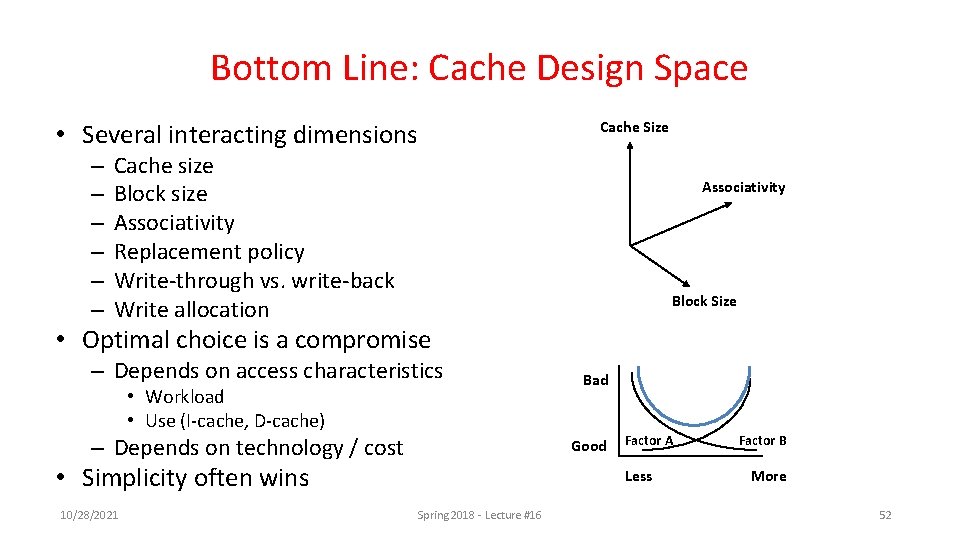
Bottom Line: Cache Design Space • Several interacting dimensions – – – Cache Size Cache size Block size Associativity Replacement policy Write-through vs. write-back Write allocation Associativity Block Size • Optimal choice is a compromise – Depends on access characteristics • Workload • Use (I-cache, D-cache) – Depends on technology / cost Good • Simplicity often wins 10/28/2021 Bad Factor A Less Spring 2018 - Lecture #16 Factor B More 52