Gravity and Oscillations OSCILLATIONS x Oscillations are caused

Gravity and Oscillations

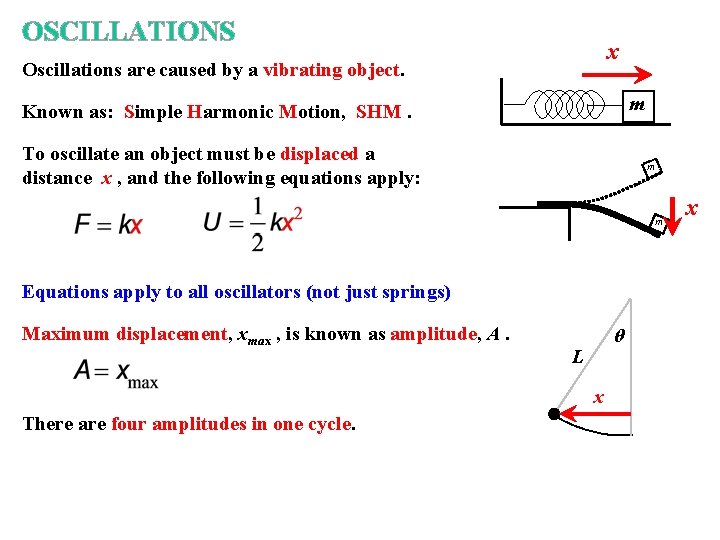
OSCILLATIONS x Oscillations are caused by a vibrating object. m Known as: Simple Harmonic Motion, SHM. To oscillate an object must be displaced a distance x , and the following equations apply: m m Equations apply to all oscillators (not just springs) Maximum displacement, xmax , is known as amplitude, A. θ L x There are four amplitudes in one cycle. x

PERIOD OF SPRINGS Oscillations are another type of cyclic motion. Period Time of one cycle For elastic devices, such as springs, there is a specific period The period of an oscillating spring depends on the mass attached to the spring, m , and the spring constant, k.

PERIOD OF SPRINGS How does doubling the mass affect the period of an oscillating spring? The new period is What mass is needed to double the period of an oscillating spring? The mass must be quadrupled

Example 1 An object completes 20 cycles in 5. 0 seconds. Determine the period. Example 2 A 500 g mass is suspended from a spring and stretches the spring 20 cm to its equilibrium position. The spring is then stretched an additional 10 cm and is released from rest. Determine the frequency of the spring’s oscillations. The key to spring problems is determining the spring constant, k. Equilibrium, where forces are equal and opposite, is the most used method.

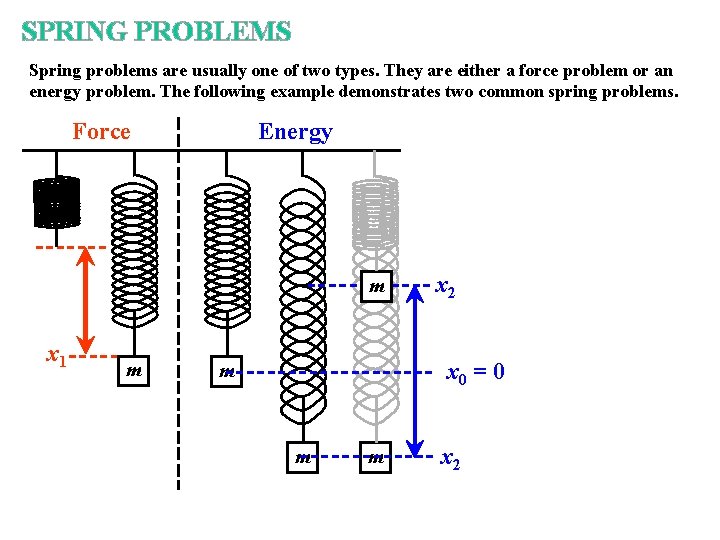
SPRING PROBLEMS Spring problems are usually one of two types. They are either a force problem or an energy problem. The following example demonstrates two common spring problems. Energy Force m x 1 m x 2 x 0 = 0 m m m x 2

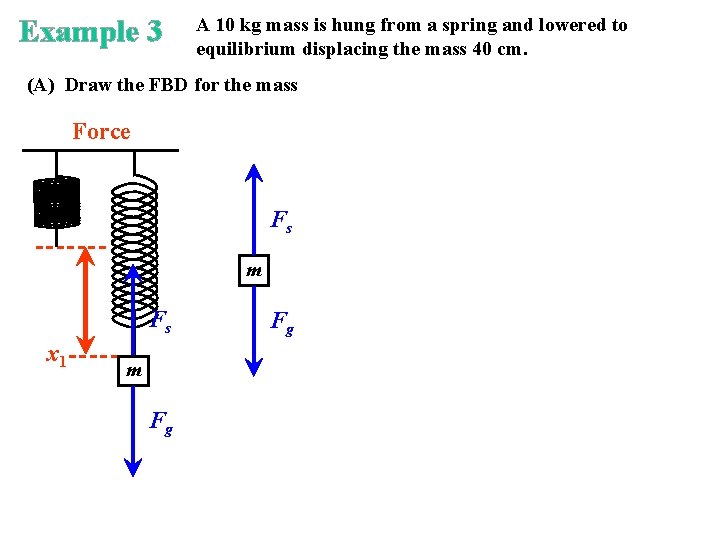
Example 3 A 10 kg mass is hung from a spring and lowered to equilibrium displacing the mass 40 cm. (A) Draw the FBD for the mass Force Fs m Fs x 1 m Fg Fg

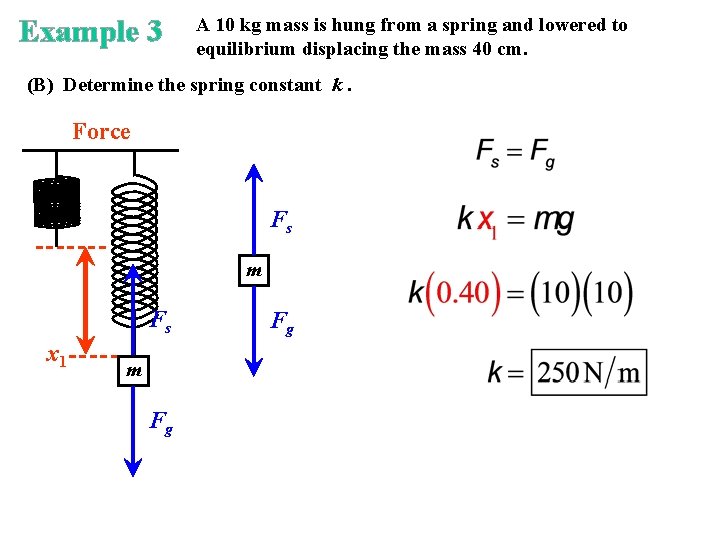
Example 3 A 10 kg mass is hung from a spring and lowered to equilibrium displacing the mass 40 cm. (B) Determine the spring constant k. Force Fs m Fs x 1 m Fg Fg

Example 3 A 10 kg mass is hung from a spring and lowered to equilibrium displacing the mass 40 cm. Energy Force As the force problem changes to an energy problem x 1 used in force no longer matters. For energy the equilibrium position becomes Fs x 1 m m Fg x 0 = 0

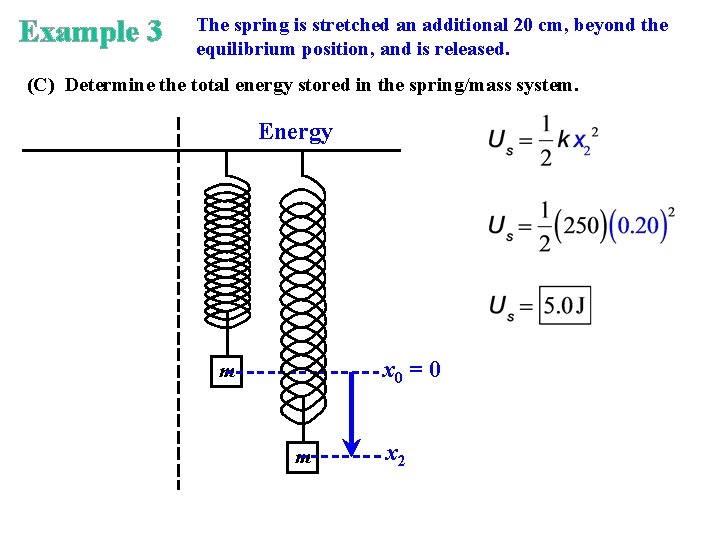
Example 3 The spring is stretched an additional 20 cm, beyond the equilibrium position, and is released. (C) Determine the total energy stored in the spring/mass system. Energy x 0 = 0 m m x 2

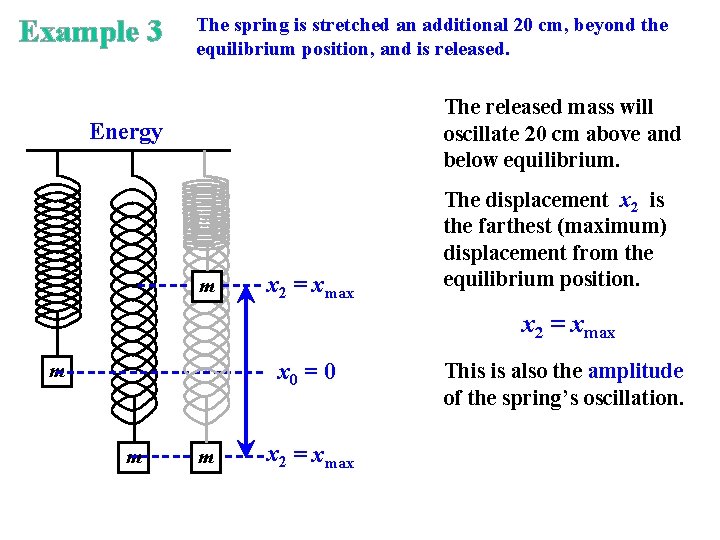
Example 3 The spring is stretched an additional 20 cm, beyond the equilibrium position, and is released. The released mass will oscillate 20 cm above and below equilibrium. Energy m x 2 = xmax The displacement x 2 is the farthest (maximum) displacement from the equilibrium position. x 2 = xmax x 0 = 0 m m m x 2 = xmax This is also the amplitude of the spring’s oscillation.

Example 3 The spring is stretched an additional 20 cm, beyond the equilibrium position, and is released. (D) Determine the speed when the mass is 10 cm from equilibrium. Use conservation of energy. Set maximum displacement as the initial position, since this is where everything is known. m 0. 20 m The displacement was given, xmax = ± 0. 20 m The velocity is always zero, v 0 = 0. 00 m m 0. 20 m

Example 3 The spring is stretched an additional 20 cm, beyond the equilibrium position, and is released. (D) Determine the speed when the mass is 10 cm from equilibrium. The final position is where information is needed. The speed, v , at 10 cm is requested. m 0. 20 m 0. 00 m m 0. 01 m m 0. 20 m Set final displacement as 10 cm, x = 0. 10 m.

Example 3 The spring is stretched an additional 20 cm, beyond the equilibrium position, and is released. (E) Determine the maximum speed during the oscillation. As before, set maximum displacement as the initial position, xmax = 0. 20 m , and v 0 = 0. m 0. 20 m m 0. 00 m m 0. 20 m Maximum speed, vmax , occurs when displacement and potential energy are zero, x = 0.

Example 3 The spring is stretched an additional 20 cm, beyond the equilibrium position, and is released. (F) Determine the period of oscillation. Period is the time of one cycle. Use the formula that is specific for a spring. m 0. 20 m The mass was given at the beginning of the problem, m = 10 kg. 0. 00 m m 0. 20 m Since period is a time, it is measured in seconds.

IMPORTANT NOTE: OSCILLATING SPRINGS AND ENERGY Clearly height was changing during the oscillation. Why was the energy associated with height, mgh , not mentioned in parts “f “ and “g” ? During a vertical oscillation, the up/down motion causes the gravitational potential energy to cancel. m 0. 20 m When a spring oscillates vertically, ignore mgh. However, if a spring moves in one direction, 0. 00 m m 0. 20 m without oscillating (such as from +xmax to −xmax ), then the potential energy of gravity, mgh , is included in the conservation of energy formula.

TRENDS IN OSCILLATIONS m +xmax x 0 = 0 m −xmax

PERIOD OF A PENDULUM For a pendulum with a string length L. Example 1 A pendulum is brought to a distant planet. The string of the pendulum is adjusted until the frequency of the pendulum swing is 1 cycle per second. The length of the string is 2. 5 m. Determine the acceleration of gravity. To solve a variable under a square root, square everything.

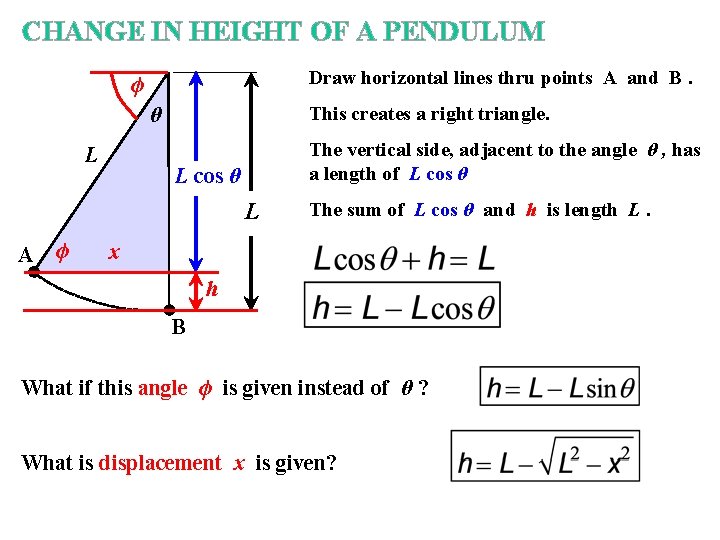
CHANGE IN HEIGHT OF A PENDULUM Draw horizontal lines thru points A and B. ϕ θ L This creates a right triangle. The vertical side, adjacent to the angle θ , has a length of L cos θ L A ϕ The sum of L cos θ and h is length L. x h B What if this angle ϕ is given instead of θ ? What is displacement x is given?

Example 4 A mass of 5. 0 kg hangs from a 1. 0 m string. The mass is displaced from point B to point A. At point A the angle that the string makes with the vertical is θ = 37 o. (A) Determine the restoring force acting on the pendulum bob when it is at point A. θ L (B) Determine the instantaneous acceleration of the pendulum bob at point A. A a Fg B The restoring force, sum of forces, and acceleration are all tangential at point A.

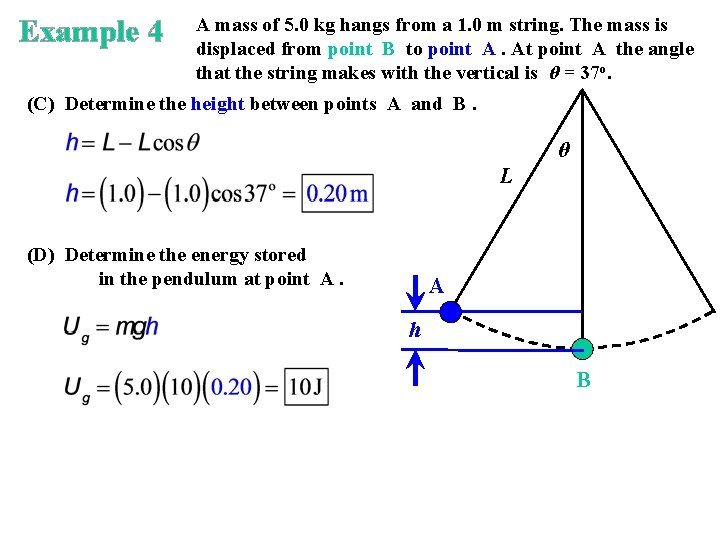
Example 4 A mass of 5. 0 kg hangs from a 1. 0 m string. The mass is displaced from point B to point A. At point A the angle that the string makes with the vertical is θ = 37 o. (C) Determine the height between points A and B. θ L (D) Determine the energy stored in the pendulum at point A. A h B

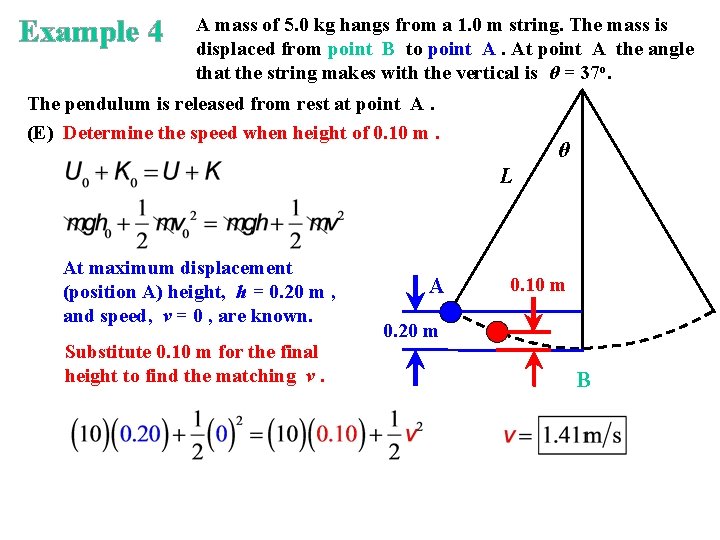
Example 4 A mass of 5. 0 kg hangs from a 1. 0 m string. The mass is displaced from point B to point A. At point A the angle that the string makes with the vertical is θ = 37 o. The pendulum is released from rest at point A. (E) Determine the speed when height of 0. 10 m. θ L At maximum displacement (position A) height, h = 0. 20 m , and speed, v = 0 , are known. Substitute 0. 10 m for the final height to find the matching v. A 0. 10 m 0. 20 m B

Example 4 A mass of 5. 0 kg hangs from a 1. 0 m string. The mass is displaced from point B to point A. At point A the angle that the string makes with the vertical is θ = 37 o. (F) Determine the maximum speed reached by the pendulum. θ L At maximum displacement (position A) height, h = 0. 20 m, and speed, v = 0 , are known. Maximum speed, vmax , occurs at equilibrium (position B), h = 0. A 0. 20 m B vmax

Example 4 A mass of 5. 0 kg hangs from a 1. 0 m string. The mass is displaced from point B to point A. At point A the angle that the string makes with the vertical is θ = 37 o. (G) Determine the period of oscillation. θ Period is the time of one cycle. Use the period of a pendulum equation. L A B Since period is a time, it is measured in seconds.

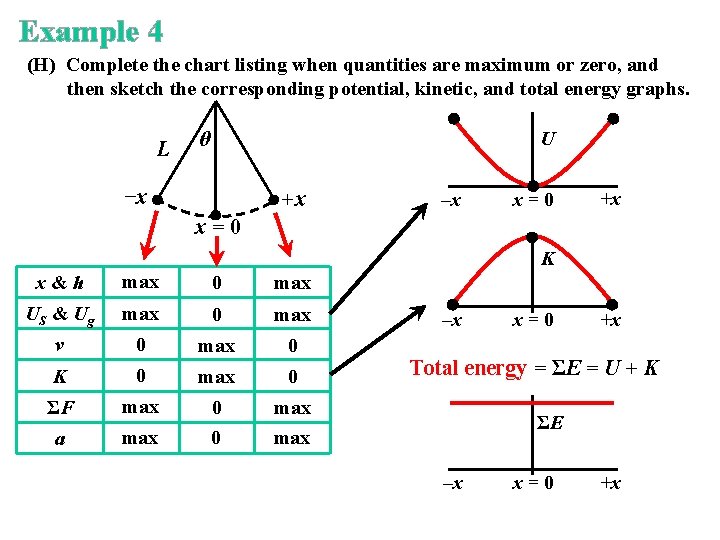
Example 4 (H) Complete the chart listing when quantities are maximum or zero, and then sketch the corresponding potential, kinetic, and total energy graphs. L θ U −x +x –x x=0 +x x=0 K x&h max 0 max US & Ug max 0 max v 0 max 0 K 0 max 0 ΣF max 0 max a max 0 max –x x=0 +x Total energy = ΣE = U + K ΣE –x x=0 +x

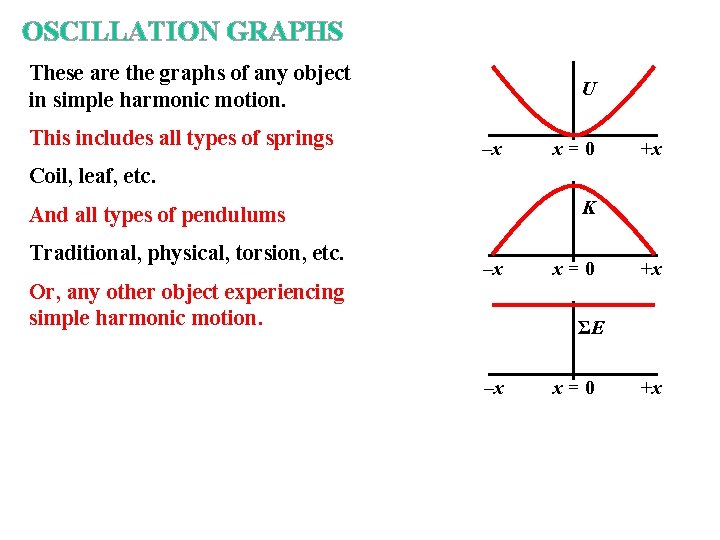
OSCILLATION GRAPHS These are the graphs of any object in simple harmonic motion. This includes all types of springs U –x x=0 +x Coil, leaf, etc. K And all types of pendulums Traditional, physical, torsion, etc. Or, any other object experiencing simple harmonic motion. –x x=0 +x ΣE –x x=0 +x

Example 5 TOTAL ENERGY AND AMPLITUDE The total energy of an oscillator is the sum of potential and kinetic energy. If energy is doubled, how does this affect amplitude of an oscillator? At amplitude: x = A and the kinetic energy is zero Doubling energy would cause the amplitude to increase by the square root of two.

Example 6 TOTAL ENERGY AND MAX SPEED The total energy of an oscillator is the sum of potential and kinetic energy. If energy is doubled, how does this affect the maximum speed of an oscillator? At maximum speed the elastic potential energy is zero. Doubling energy would cause the maximum speed to increase by the square root of two.