Gravitational Waveforms from Coalescing Binary Black Holes DaeIl

Gravitational Waveforms from Coalescing Binary Black Holes Dae-Il (Dale) Choi NASA Goddard Space Flight Center, MD, USA Universities Space Research Association, USA Supported by NASA ATP 02 -0043 -0056 & NASA Advanced Supercomputing Project “Columbia” Numerical Relativity 2005 Workshop NASA Goddard Space Flight Center, Greenbelt, MD, NOV 2, 2005

Collaborators Beyond Einstein: From the Big Bang to Black Holes It’s teamwork Joan Centrella, John Baker (NASA/GSFC) Jim van Meter, Michael Koppitz (National Research Council) Breno Imbiriba, W. Darian Boggs, Stefan Mendez-Diez (University of Maryland) Other collaborators J. David Brown (North Carolina State Univ. ) David Fiske (DAC, formerly NASA/GSFC) Kevin Olson (NASA/GSFC) Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 2

Outline Beyond Einstein: From the Big Bang to Black Holes Methodology: Hahndol Code [Hahndol=한돌=translation of “Ein-stein” into Korean] Results: Inspiral merger from the ISCO (QC 0) Results: Head-on collision (if time allows) Movie of the real part of Psi 4 Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 3

Hahndol Code Beyond Einstein: From the Big Bang to Black Holes 3+1 Numerical Relativity Code – BSSN formalism following Imbiriba et al, PRD 70, 124025 (2004), Alcubierre at al PRD 67, 084023 (2003) except the new gauge conditions. – Uses finite differencing (mixed 2 nd and 4 th order FD, Mesh-Adapted- Differencing–see posters for details), iterative Crank-Nicholson time integrator. – Computational infrastructure based on PARAMESH (Mac. Niece, Olson) Scalability shown up to 864 CPUs with ~ 95% efficiency. Mesh refinement – Currently use fixed mesh structure with mesh boundaries at (2, 4, 8, 16, 32, 64)M for QC 0 runs. – The innermost level contains the both black holes. – For higher QC-sequence, AMR implementation being tested. Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 4

Hahndol Code Beyond Einstein: From the Big Bang to Black Holes Outer boundary conditions – Impose outgoing Sommerfeld conditions on all BSSN variables. – But, basic strategy is to push OB far away so that OB does not contaminate regions of interests. – With OB=128 M, no harmful effects on the dynamics of black holes nor waveform extraction (QC 0). If desired, OB can be put at 256 M or beyond. Initial data solver – Uses multi-grid method on a non-uniform grid using Brown’s algorithm: Brown & Lowe, JCP 209, 582 -598, 2005 (gr-qc/0411112). – Generate QC ID by solving HCE using puncture method (Brandt & Bruegmann, 1997). – Bowen-York prescription for the extrinsic curvature for binary black holes. Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 5

Hahndol Code Beyond Einstein: From the Big Bang to Black Holes Traditional gauge conditions (AEI, etc. ) – Split conformal factor into time-indep. singular part (ΨBL) and time-dep. regular part. Treat ΨBL analytically and evolve only the regular part. – Use the following K-/Gamma-driver conditions for gauges. (BL factor) – Problem is that, because of ΨBL factor, black holes cannot move. – Requires co-rotation shift. But it involves superluminal shift. Alternative gauge conditions – Do not split into singular/regular part. No BL factor. – Combined with the driver conditions, let the black holes move across the grid. – Does this really work? Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 6

Hahndol Code Beyond Einstein: From the Big Bang to Black Holes Not so fast! Two concerns. – (a) Puncture memory effect: BHs move but still spiky errors at where the punctures were at t=0. – (b) Messy stuff near the would-have-been puncture locations if they were moving. The problem (a) – Caused by the zero-speed mode in the Gamma driver shift condition – Can be alleviated by “shifting shift” [Movies] comparison bet. (1) Traditional (crashed at t=35 M) (2) No BL factor (3) No. BL + Shifting Shift Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 7

Hahndol Code Beyond Einstein: From the Big Bang to Black Holes The problem (b) – In practice, we find that the stuff doesn’t seem to “spill over”. – [Movie: Head-on collision w/ L/M~9 using No. BL+Shifting Shift] shows a good convergence of HC from 3 runs with different resolutions. – Note, with the traditional gauge, HC too large and non-convergent. For all the cases we considered, this new gauge conditions allow us to obtain convergent results (constraints, waveforms). Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 8

Hahndol Code Beyond Einstein: From the Big Bang to Black Holes Wave extraction – Compute the Newman-Penrose Weyl scalar Ψ 4 (a gauge invariant measure) where C is weyl tensor and (l, n, m, mbar) is a tetrad. – Analyze its harmonic decomposition using a novel technique due to Misner (Misner 2004; Fiske 2005). – Compute waveforms r ~ 20 M, 30 M, 40 M and 50 M. Coulomb scalar χ [Beetle, et al, PRD 72, 024013 (2005); Burko, Baumgarte & Beetle, gr-qc/0505028. ] Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 9

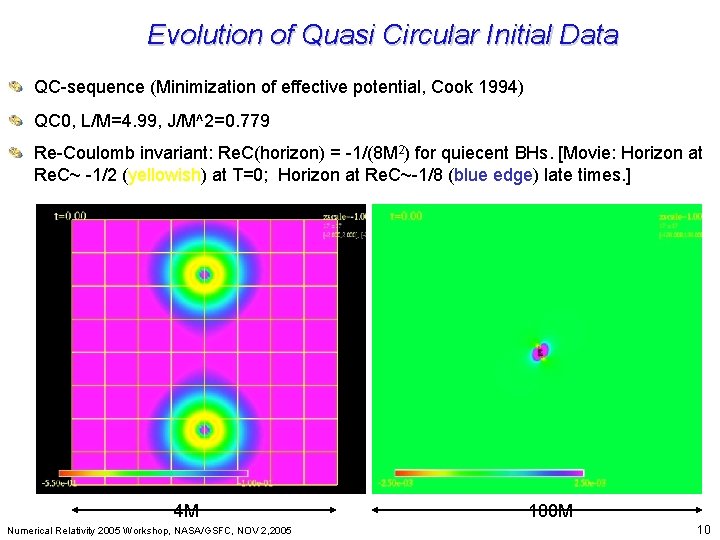
Evolution of Quasi Circular Initial Data Beyond Einstein: From the Big Bang to Black Holes QC-sequence (Minimization of effective potential, Cook 1994) QC 0, L/M=4. 99, J/M^2=0. 779 Re-Coulomb invariant: Re. C(horizon) = -1/(8 M 2) for quiecent BHs. [Movie: Horizon at Re. C~ -1/2 (yellowish) at T=0; Horizon at Re. C~-1/8 (blue edge) late times. ] 4 M Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 180 M 10

QC 0 (BH source region) Beyond Einstein: From the Big Bang to Black Holes Comparison of Re (Coulomb) scalar for three different resolutions: M/16, M/32, M/48 runs. [Only in this movie, time label is in terms of (M/2)] (In this talk, different runs are labeled by the resolution in the finest resolution grid. ) Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 11

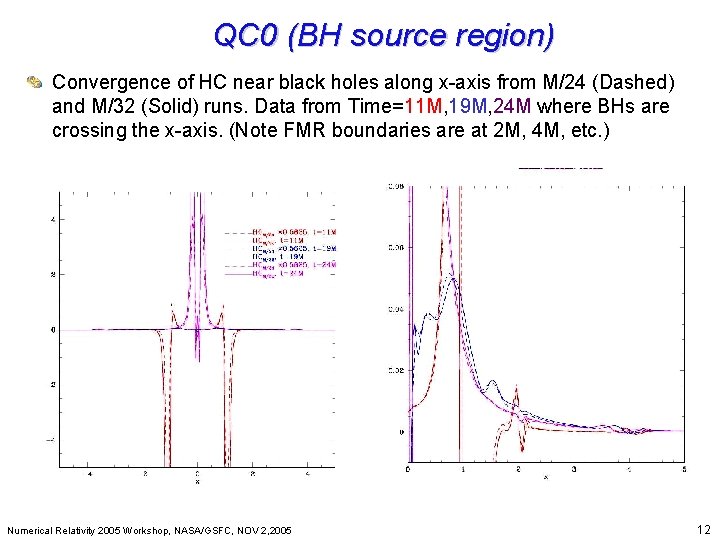
QC 0 (BH source region) Beyond Einstein: From the Big Bang to Black Holes Convergence of HC near black holes along x-axis from M/24 (Dashed) and M/32 (Solid) runs. Data from Time=11 M, 19 M, 24 M where BHs are crossing the x-axis. (Note FMR boundaries are at 2 M, 4 M, etc. ) Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 12

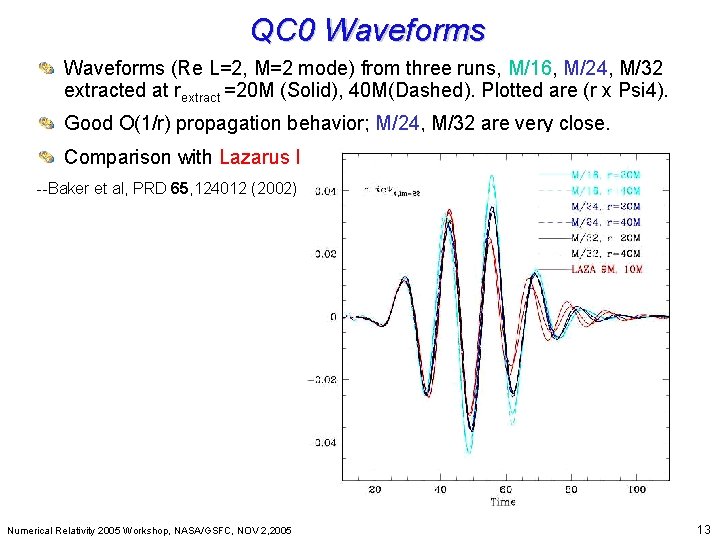
QC 0 Waveforms Beyond Einstein: From the Big Bang to Black Holes Waveforms (Re L=2, M=2 mode) from three runs, M/16, M/24, M/32 extracted at rextract =20 M (Solid), 40 M(Dashed). Plotted are (r x Psi 4). Good O(1/r) propagation behavior; M/24, M/32 are very close. Comparison with Lazarus I --Baker et al, PRD 65, 124012 (2002) Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 13

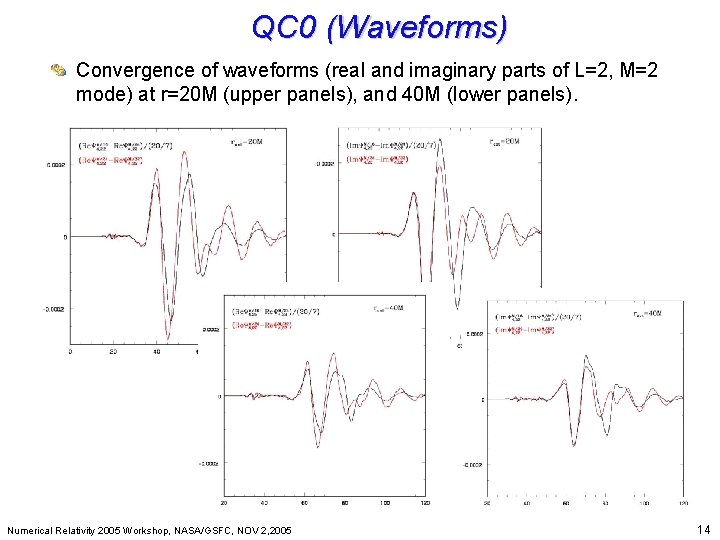
QC 0 (Waveforms) Beyond Einstein: From the Big Bang to Black Holes Convergence of waveforms (real and imaginary parts of L=2, M=2 mode) at r=20 M (upper panels), and 40 M (lower panels). Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 14

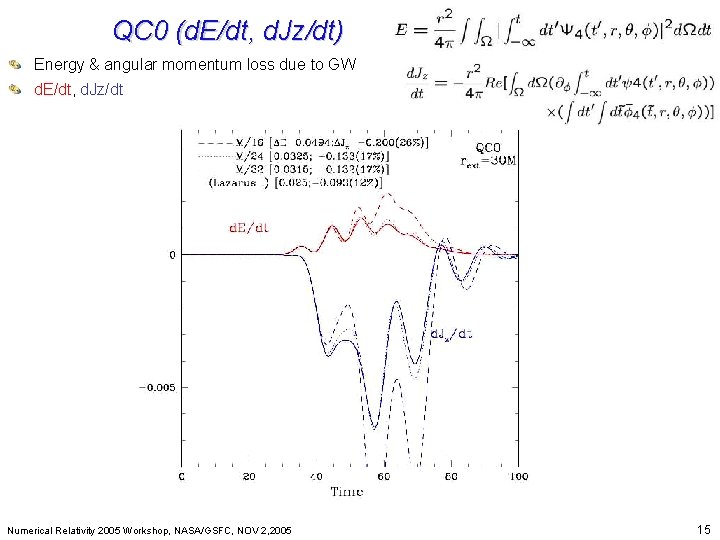
QC 0 (d. E/dt, d. Jz/dt) Beyond Einstein: From the Bigdue Bangto to. GW Black Holes Energy & angular momentum loss d. E/dt, d. Jz/dt Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 15

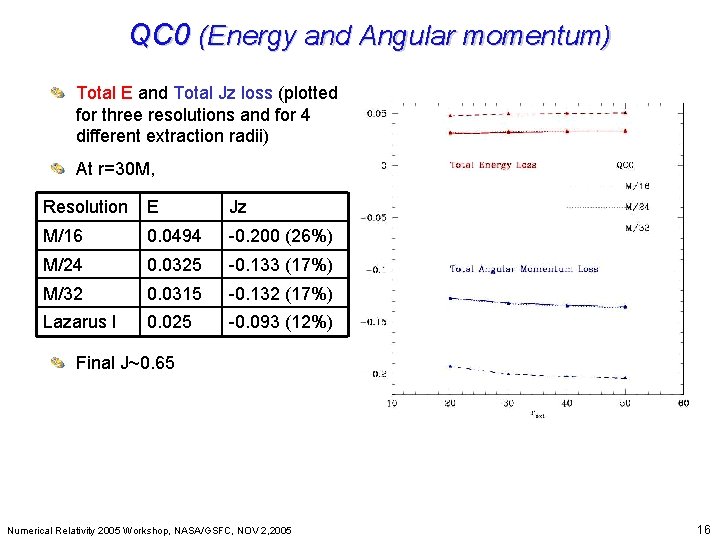
QC 0 (Energy and Angular momentum) Beyond Einstein: From the Big Bang to Black Holes Total E and Total Jz loss (plotted for three resolutions and for 4 different extraction radii) At r=30 M, Resolution E Jz M/16 0. 0494 -0. 200 (26%) M/24 0. 0325 -0. 133 (17%) M/32 0. 0315 -0. 132 (17%) Lazarus I 0. 025 -0. 093 (12%) Final J~0. 65 Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 16

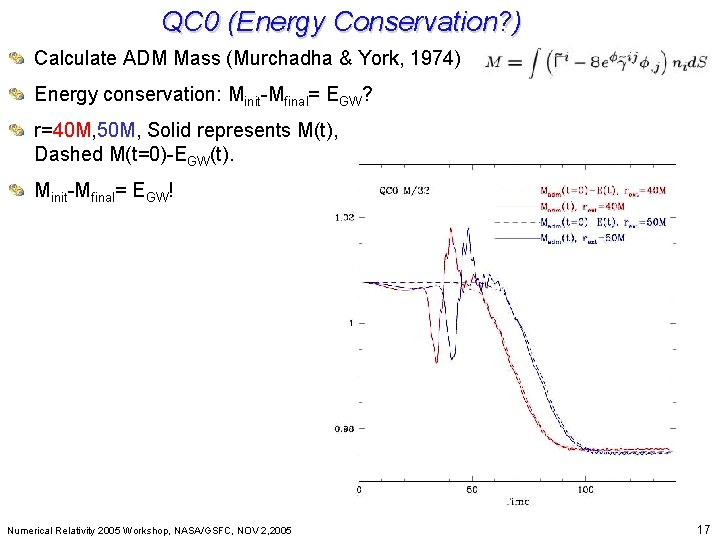
QC 0 (Energy Conservation? ) Calculate ADM Mass (Murchadha & York, Beyond Einstein: From the Big Bang to Black Holes 1974) Energy conservation: Minit-Mfinal= EGW? r=40 M, 50 M, Solid represents M(t), Dashed M(t=0)-EGW(t). Minit-Mfinal= EGW! Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 17

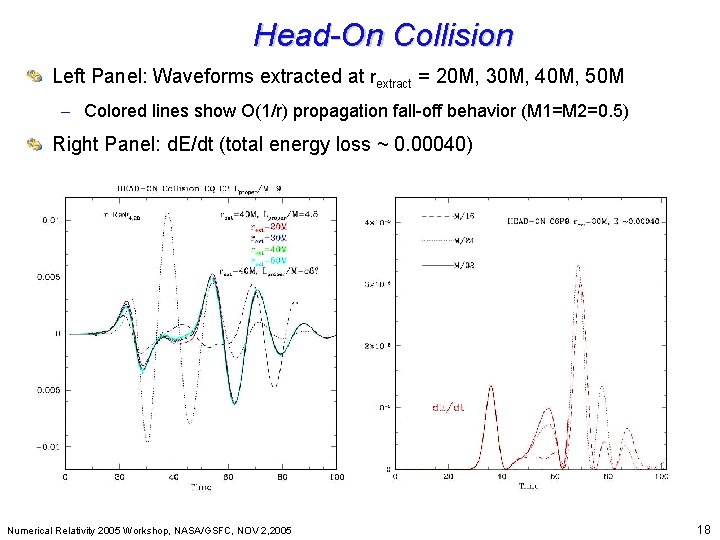
Head-On Collision Beyond Einstein: From the Big Bang to Black Holes Left Panel: Waveforms extracted at rextract = 20 M, 30 M, 40 M, 50 M – Colored lines show O(1/r) propagation fall-off behavior (M 1=M 2=0. 5) Right Panel: d. E/dt (total energy loss ~ 0. 00040) Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 18

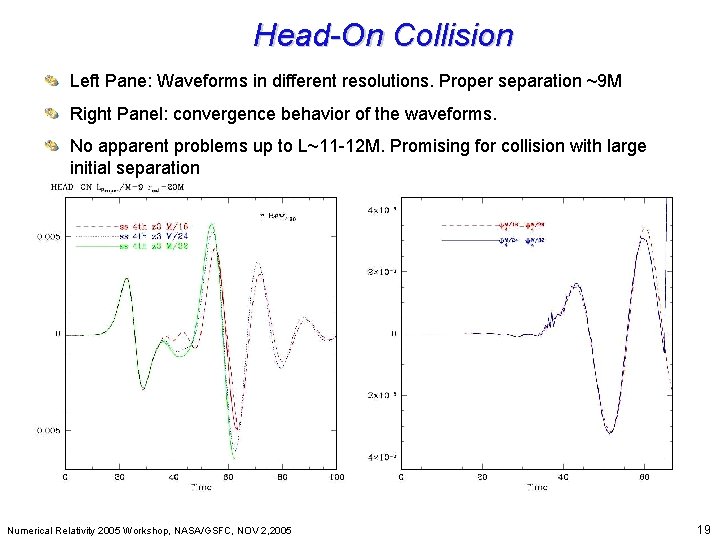
Head-On Collision Beyond Einstein: From the Big Bang to Black Holes Left Pane: Waveforms in different resolutions. Proper separation ~9 M Right Panel: convergence behavior of the waveforms. No apparent problems up to L~11 -12 M. Promising for collision with large initial separation Numerical Relativity 2005 Workshop, NASA/GSFC, NOV 2, 2005 19