Gravitational Field Gravitational Potential Energy AP Physics C











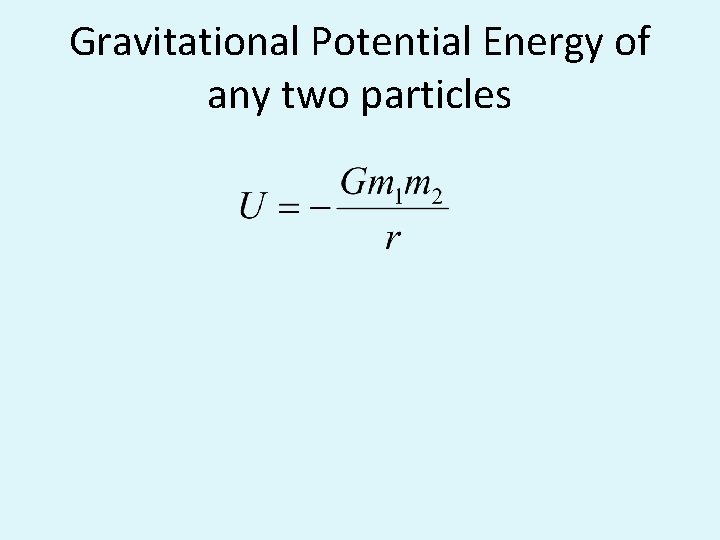





- Slides: 22

-Gravitational Field -Gravitational Potential Energy AP Physics C Mrs. Coyle

Remember: Newton’s Law of Universal Gravitation -Universal Gravitation Constant G=6. 67 x 1011 Nm 2/kg 2 -The gravitational force is a field force.

Review Question: Question • Which exerts a greater force, the earth on the moon or the moon on the earth?

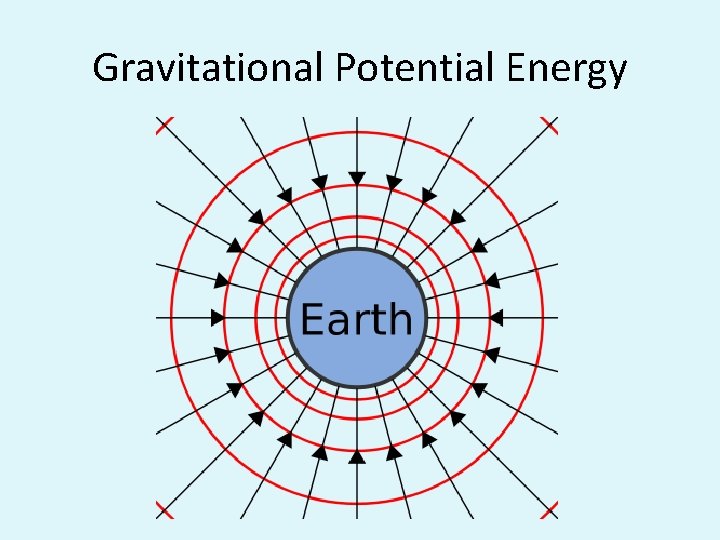
• Gravitational Field: the t space around a mass. Here a test mass would feel a gravitational force. • Gravitational Field Vector:

Gravitational Field Vector, g at the surface of the Earth

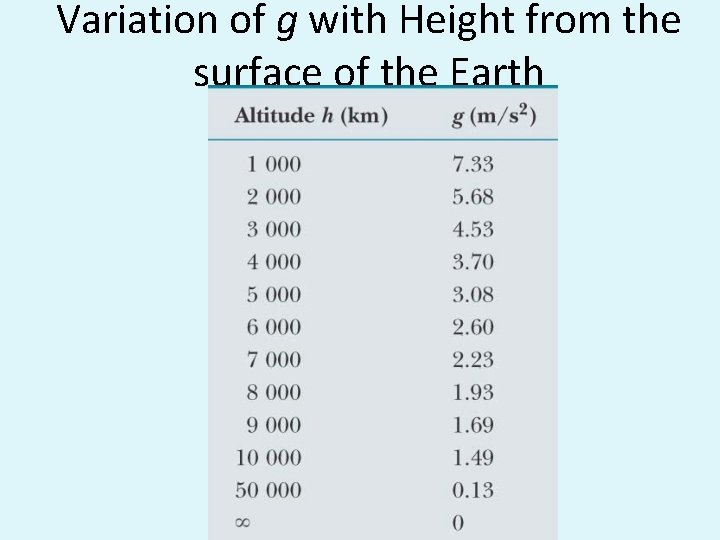
g above the Earth’s surface • r = RE + h Note: • g decreases with increasing altitude • As r ® , the weight of the object approaches zero

Variation of g with Height from the surface of the Earth

Remember • The gravitational force is conservative • The gravitational force is a central force (A central force has a direction towards the center and its magnitude depends only on r) • A central force can be represented by

Work done by the Gravitational Force • A particle moves from A to B while acted on by a central force F • We approximate the path along A to B with radial and arc zigzags • The work done by F along the arcs is zero • The work done by F along the radial direction is

Work done by the Gravitational Force • The work done is independent of the path and depends only on rf and ri • This proves that the gravitational force is conservative.

Gravitational Potential Energy • As a particle moves from A to B, its gravitational potential energy changes by:

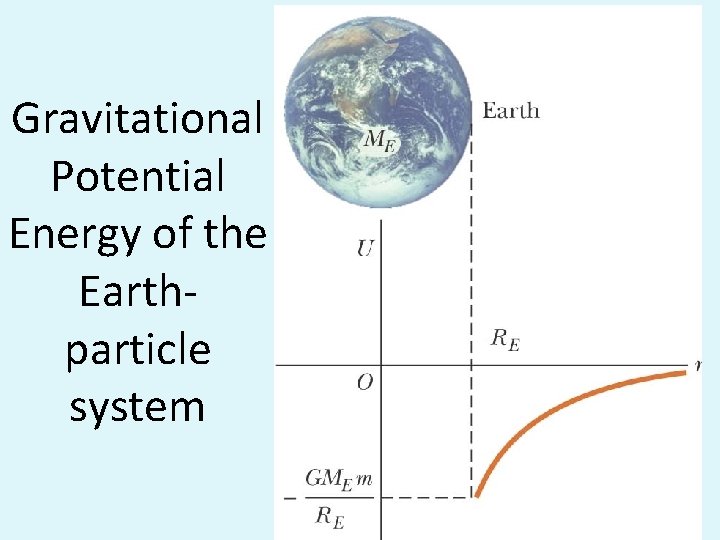
Gravitational Potential Energy of the Earth-particle system • The reference point is chosen at infinity where the force on a particle would approach zero. Ui = 0 for ri = • ∞This is valid only for r < RE > =RE and not valid • U is negative because of the choice of Ui

Gravitational Potential Energy of the Earthparticle system
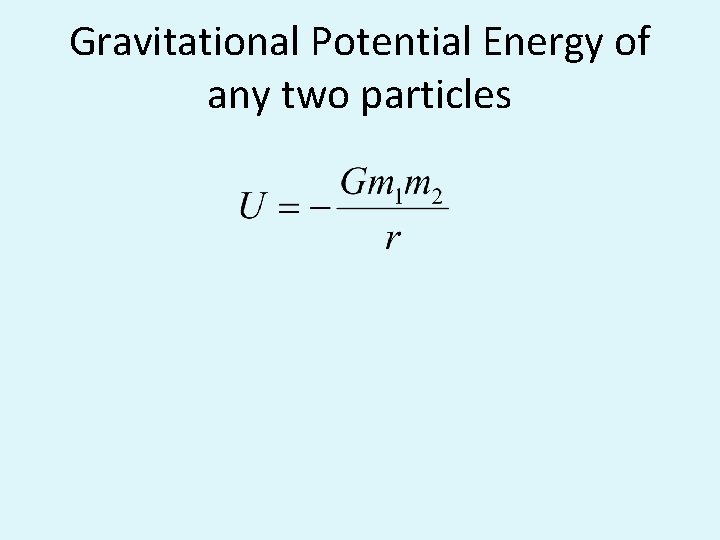
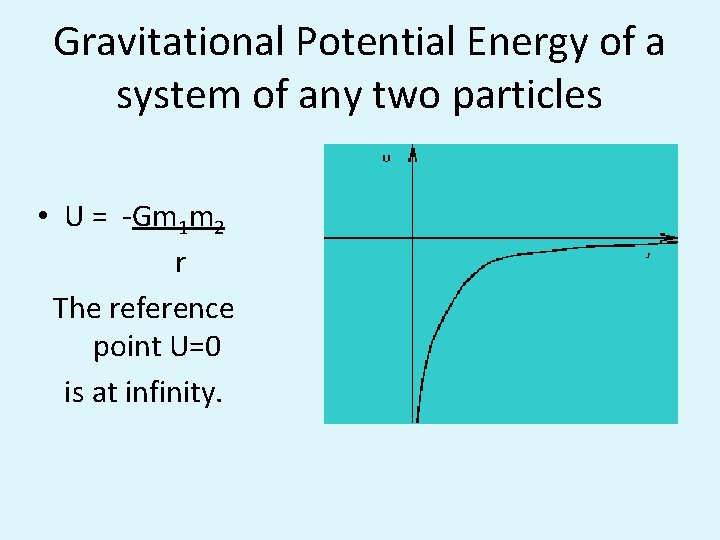
Gravitational Potential Energy of any two particles

Gravitational Potential Energy of a system of any two particles • U = -Gm 1 m 2 r The reference point U=0 is at infinity.

Gravitational Potential Energy

Gravitational Potential Energy • An outside force must do positive work to increase the separation between two objects • This work gives the objects a greater potential energy (less negative).

Binding Energy • The absolute value of the potential energy is the binding energy • An outside force must supply energy gretaer or equal to the binding energy to separate the particles to an infinite distance of separation. • The excess energy will be in the form of kinetic energy of the particles when they are at infinite separation.

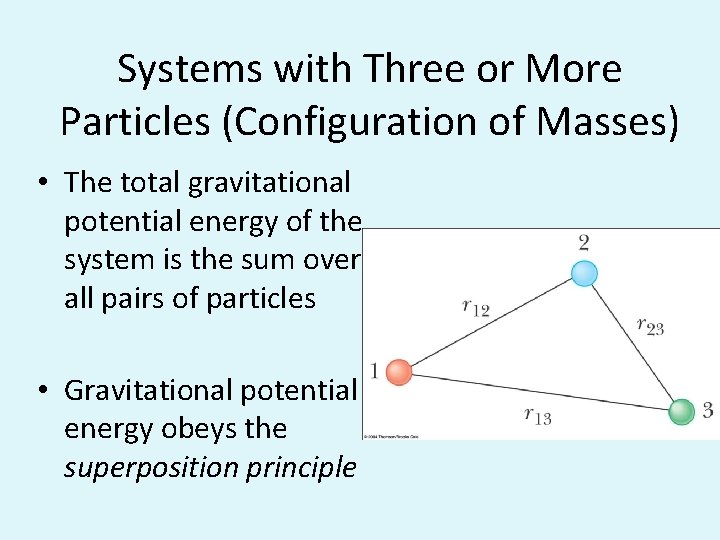
Systems with Three or More Particles (Configuration of Masses) • The total gravitational potential energy of the system is the sum over all pairs of particles • Gravitational potential energy obeys the superposition principle

Systems with Three Particles • The absolute value of Utotal represents the work needed to separate the particles by an infinite distance. • Remember energy is a scalar quantity.

Configurations of Masses • Gravitational Forces are added using the vector component method. • To find the Gravitational Potential Energy of the configuration of masses, the individual energies are added as scalars. • A force would have to supply an amount of energy equal to the individual energy in order to separate the masses by an infinite distance.

Ex #31 • A system consists of three particles, each of mass 5. 00 g, located at the corners of an equilateral triangle with sides of 30. 0 cm. a) Calculate the potential energy of the system. b) If the particles are released simultaneously, where will they collide? Ans: a) -1. 67 x 10 -14 J
 Kinetic energy gravitational
Kinetic energy gravitational Gravitational potential energy vs kinetic energy
Gravitational potential energy vs kinetic energy How is potential energy used
How is potential energy used Gravitational potential energy
Gravitational potential energy Gravitational potential energy
Gravitational potential energy Work done by normal force
Work done by normal force What is potential energy
What is potential energy Examples of mechanical energy
Examples of mechanical energy Gpe= mgh
Gpe= mgh Gravitational potential energy
Gravitational potential energy Potential energy equation
Potential energy equation Formula of kinetic energy
Formula of kinetic energy Gravitational potential energy
Gravitational potential energy Mechanical advantage
Mechanical advantage Efficiency formula
Efficiency formula Energy formula
Energy formula Unit of potential
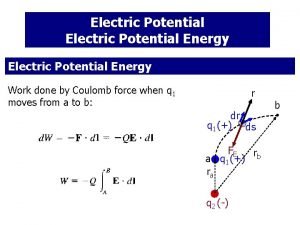
Unit of potential Electric potential
Electric potential V = pe/q
V = pe/q A uniformly charged conducting sphere
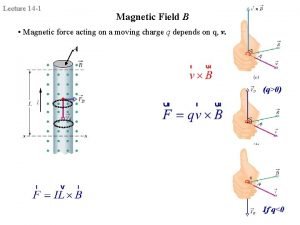
A uniformly charged conducting sphere Magnetic field in a closed loop
Magnetic field in a closed loop Potential energy of an electric field
Potential energy of an electric field Potential energy magnetic field
Potential energy magnetic field