GRAVD Part II Examining airborne gravity processing assumptions

GRAV-D Part II : Examining airborne gravity processing assumptions with an aim towards producing a better gravimetric geoid Theresa Diehl*, Sandra Preaux, Vicki Childers, Dan Roman, Dru Smith, and Jarir Saleh

GRAV-D Project Goals • NGS’ official policy: Gravity for the Redefinition of the American Vertical Datum • To create a 1 -2 cm accuracy gravimetric geoid • Requirements: – Acquiring highly accurate airborne gravity data across data the country – Blending the airborne data with satellite gravity (GRACE, GOCE) – Evaluating and then blending in existing surface gravity data (plus collecting new data)

A Critical Examination of Airborne Gravity Processing • Geophysical modeling requires errors of 1 m. Gal at best, often 3 m. Gals or more. • Some gravity processing equations were derived in 1960 s, when precise-positioning was not possible • Assumptions were made to simplify equations and provide efficient calculation • Now, geodesy for a gravimetric geoid requires accounting for small errors

Airborne Gravity Processing • Corrections/assumptions applied to raw data: – – – Terrestrial Gravity Tie Instrument drift Aircraft vertical acceleration correction (from GPS) A model ellipsoid and/or geoid as datum Normal (a. k. a. theoretical) gravity Eotvos (accounts for motion in a moving reference frame) – Free-Air correction (involves height above datum) – Off-level correction

Terrestrial Gravity Tie • Absolute gravity sites not necessarily near airport and most recent occupations vary in time. • So, we do all new absolute gravity readings and ties. • Set new gravity marks where necessary and at each airport of operations, for future use.
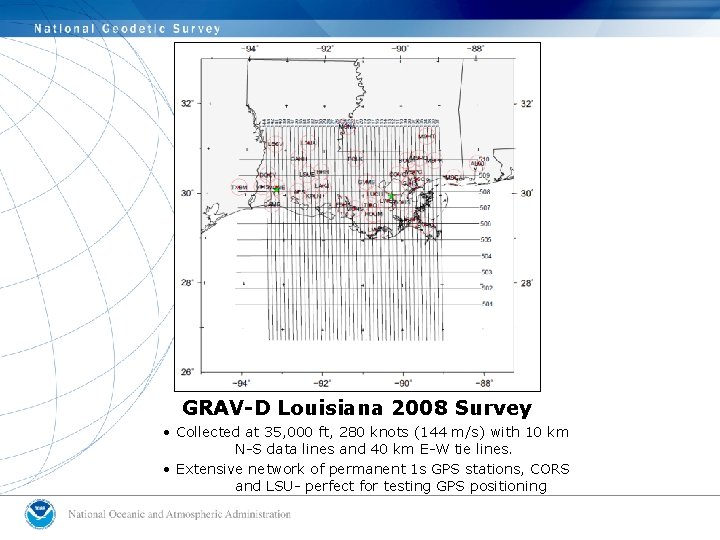
GRAV-D Louisiana 2008 Survey • Collected at 35, 000 ft, 280 knots (144 m/s) with 10 km N-S data lines and 40 km E-W tie lines. • Extensive network of permanent 1 s GPS stations, CORS and LSU- perfect for testing GPS positioning
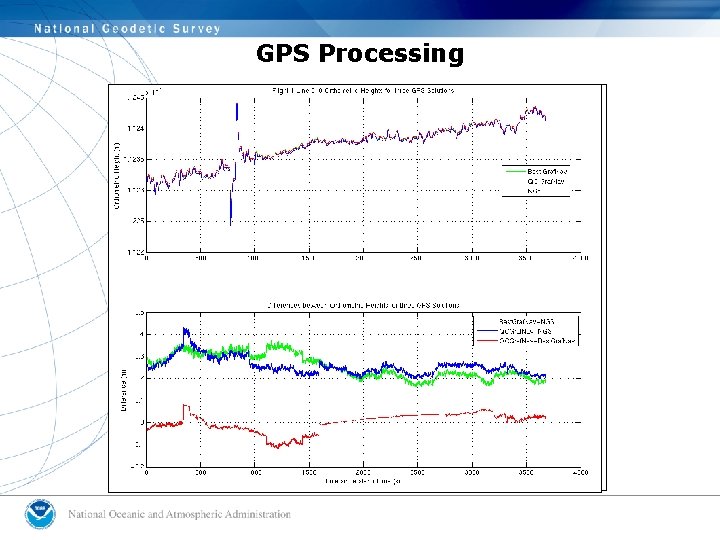
GPS Processing
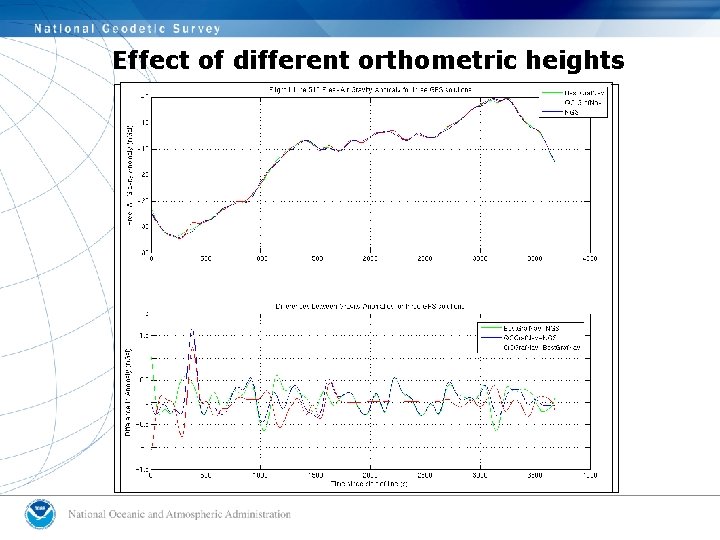
Effect of different orthometric heights
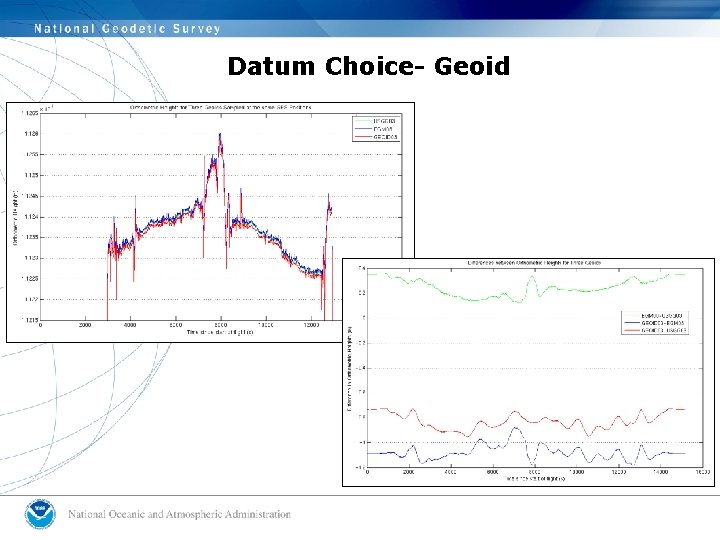
Datum Choice- Geoid
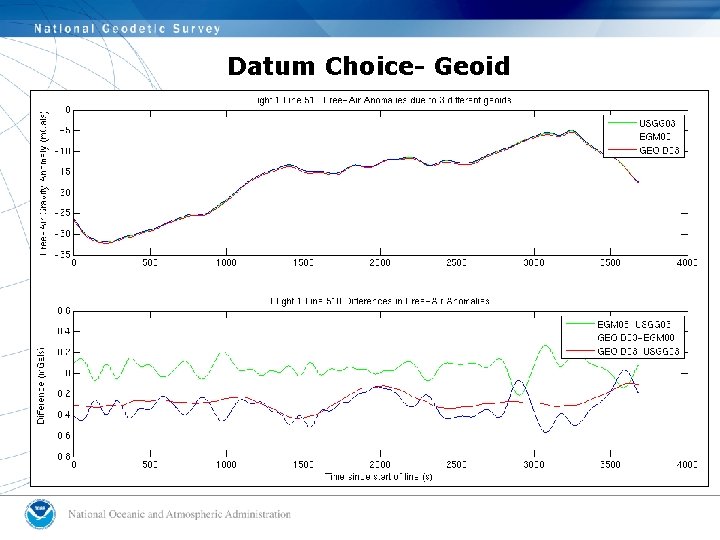
Datum Choice- Geoid
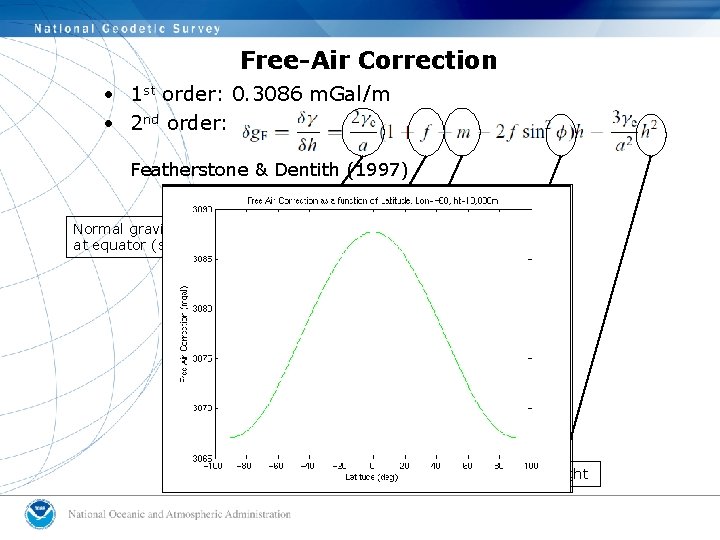
Free-Air Correction • 1 st order: 0. 3086 m. Gal/m • 2 nd order: Featherstone & Dentith (1997) Normal gravity at equator/ radius at equator (semi-major axis) Flattening of ellipsoid Geodetic parameter= ratio of gravitational and centrifugal forces at equator Geocentric Latitude Ellipsoidal height

Eotvos Correction • Classic text: Harlan (1968) • Provides – a full-vector equation that requires knowledge of position in a moving reference frame – an approximation appropriate for jet speeds, less precisely positioned • “Accelerations of 1 m. Gal should be considered in order to keep the total error within 10 m. Gal. ” That is accomplished by dropping 2 nd order terms and introducing an ellipsoid model into the equation.
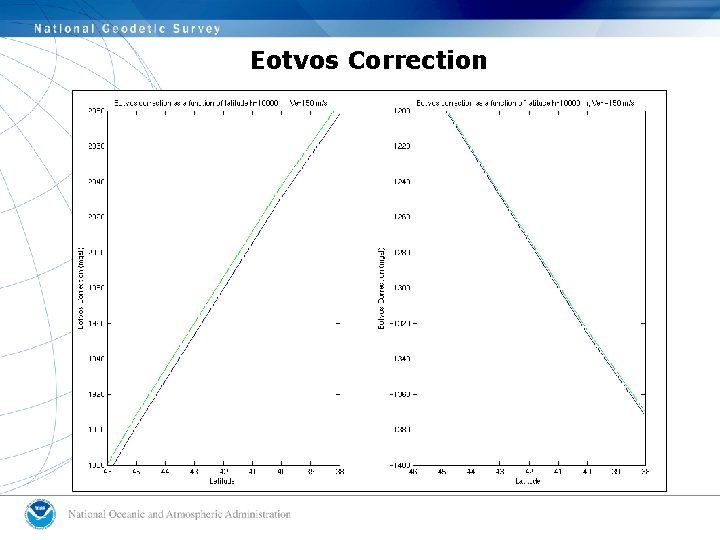
Eotvos Correction

Summary: Effects of processing assumptions on free-air gravity anomalies • An accounting finds that: – Differences in GPS yield gravity differences +/-1 m. Gal – Differences in geoid yield gravity differences +/- 0. 2 m. Gal and a -0. 4 m. Gal bias for Geoid 03 – 2 nd order free-air correction yields gravity differences of up to 1 m. Gal due only to height, up to 1. 8 m. Gals at high latitude and low altitude, and up to 18 m. Gals at high latitude and high altitude – Full-vector Eotvos correction yields gravity differences up to +/-7 m. Gal, dependent on your latitude. • Other processing steps still need to be examined

Just a word on: Off-level Correction • Active debate on how to do this • • Swain (1996) Peters and Brozena (1995) Oleson (Ph. D. Thesis) Ridgeway (2008)
- Slides: 15