GRASP SAT solver J MarquesSilva and K Sakallah

GRASP SAT solver J. Marques-Silva and K. Sakallah Presented by Ed Clarke Slides borrowed from P. Chauhan and C. Bartzis

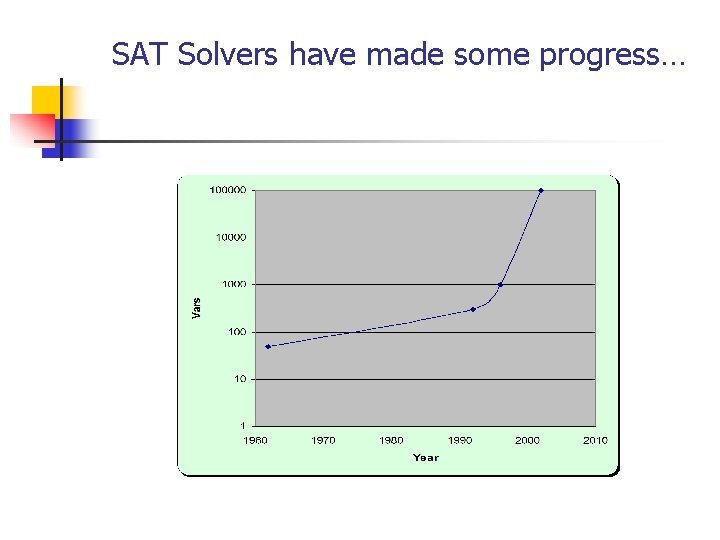
SAT Solvers have made some progress…

Conjunctive Normal Form (CNF) Atomic proposition: x 1, x 2, x 3, … n Literal: xi or xi where xi is atomic n Clause: l 1 l 2 … ln where li is a literal n CNF formula: 1 2 … m where i is a clause n Example: (x 2 x 3) ( x 1 x 4 x 3) ( x 2 x 4) n

Putting a formula in CNF n n n Extract from truth table of formula Put in Negation Normal Form (using De Morgan’s laws) and expand using distributivity of over : p (q r) (p q) (p r) Put in Negation Normal Form and introduce new variable for each conjunctive subformula. (equi-satisfiable but not logically equivalent)

What is SAT? n n Given a propositional formula in CNF, find an assignment to boolean variables that makes the formula true E. g. 1 = (x 2 x 3) 2 = ( x 1 x 4) 3 = ( x 2 x 4) A = {x 1=0, x 2=1, x 3=0, x 4=1} SATisfying assignment!

Why is SAT important? n n Fundamental problem from theoretical point of view Numerous applications n n CAD, VLSI Optimization Model Checking and other kinds of formal verification AI, planning, automated deduction

Terminology n CNF formula n n n x 1, …, xn: n variables 1, …, m: m clauses Assignment A n n n 1 = (x 2 x 3) 2 = ( x 1 x 4 ) 3 = ( x 2 x 4 ) A = {x 1=0, x 2=1, x 3=0, x 4=1} Set of (x, v(x)) pairs |A| < n partial assignment {(x 1, 0), (x 2, 1), (x 4, 1)} |A| = n complete assignment {(x 1, 0), (x 2, 1), (x 3, 0), (x 4, 1)} |A= 0 unsatisfying assignment {(x 1, 1), (x 4, 1)} |A= 1 satisfying assignment {(x 1, 0), (x 2, 1), (x 4, 1)} |A= X unresolved {(x 1, 0), (x 2, 0), (x 4, 1)}

Terminology n An assignment partitions the clause database into three classes n Satisfied n Unsatisfied n Unresolved n Free literals: unassigned literals of a clause n Unit clause: unresolved with only one free literal

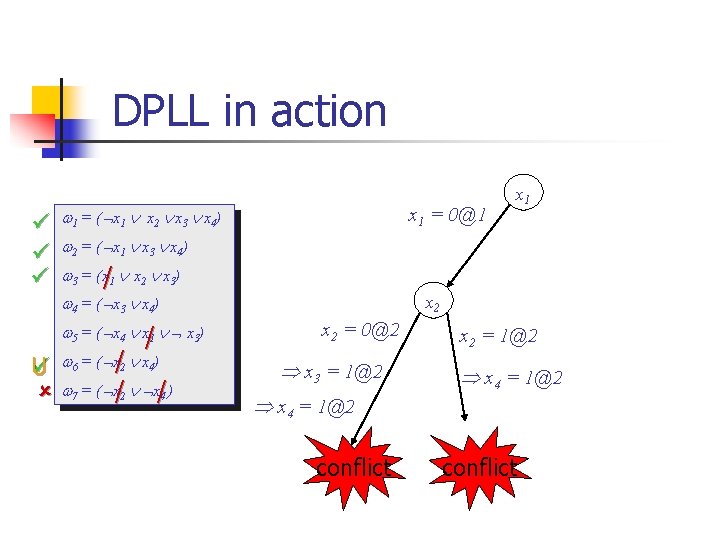
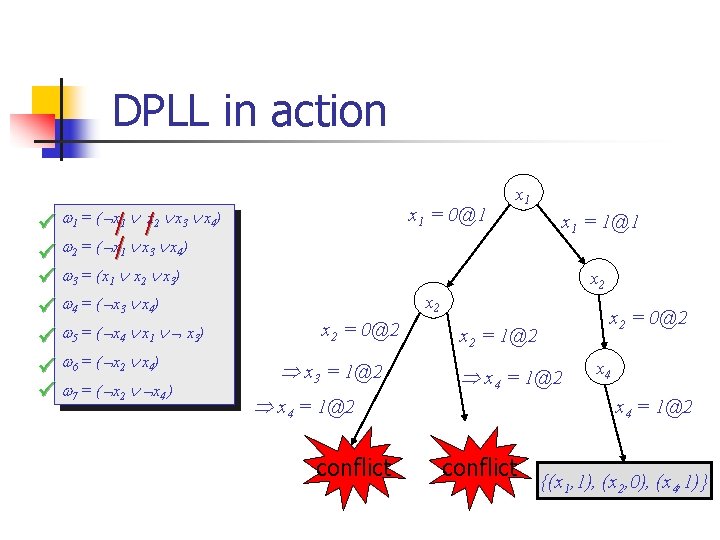
Basic Backtracking Search Organize the search in the form of a decision tree n n Each node is an assignment, called decision assignment Depth of the node in the decision tree decision level (x) x=v@d x is assigned to v at decision level d

Basic Backtracking Search n Iteration: 1. 2. Make new decision assignments to explore new regions of search space Infer implied assignments by a deduction process. n 3. May lead to unsatisfied clauses, conflict. The assignment is called conflicting assignment. If there is a conflict backtrack

DPLL in action U U x 1 = 0@1 1 = ( x 1 x 2 x 3 x 4) 2 = ( x 1 x 3 x 4) 3 = (x/1 /x 2 x 3) 4 = ( x/3 x 4) 5 = ( x/4 x/1 x/3) 6 = ( x 2 x 4) 7 = ( x 2 x 4 ) x 2 = 0@2 x 3 = 1@2 x 4 = 1@2 conflict x 1

DPLL in action x 1 = 0@1 1 = ( x 1 x 2 x 3 x 4) 2 = ( x 1 x 3 x 4) 3 = (x/1 x 2 x 3) x 2 4 = ( x 3 x 4) 5 = ( x 4 x/1 x 3) U x 1 6 = ( x/2 x 4) 7 = ( x/2 x/4 ) x 2 = 0@2 x 3 = 1@2 x 2 = 1@2 x 4 = 1@2 conflict

DPLL in action 1 = ( x/1 /x 2 x 3 x 4) 2 = ( x/1 x 3 x 4) 3 = (x 1 x 2 x 3) 4 = ( x 3 x 4) 5 = ( x 4 x 1 x 3) 6 = ( x 2 x 4) 7 = ( x 2 x 4 ) x 1 = 0@1 x 1 = 1@1 x 2 x 2 = 0@2 x 3 = 1@2 x 2 = 1@2 x 4 = 1@2 conflict x 2 = 0@2 x 4 = 1@2 conflict {(x 1, 1), (x 2, 0), (x 4, 1)}

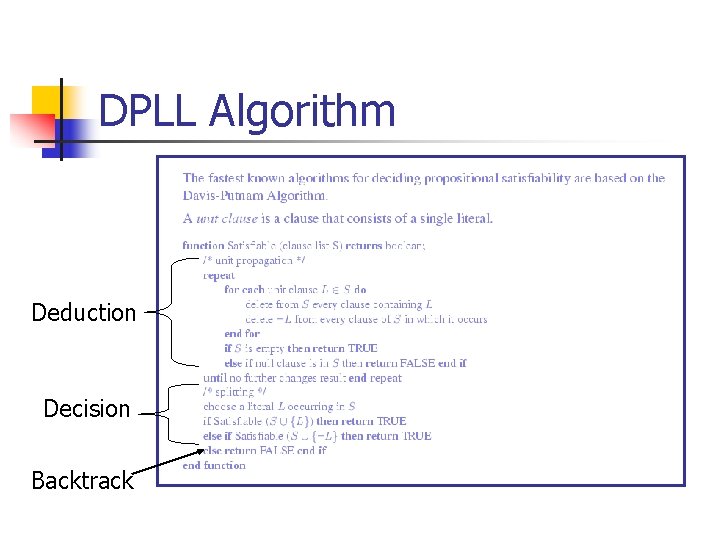
DPLL Algorithm Deduction Decision Backtrack

GRASP n n GRASP stands for Generalized sea. Rch Algorithm for the Satisfiability Problem (Silva, Sakallah, ’ 96) Features: n n n Implication graphs for BCP and conflict analysis Learning of new clauses Non-chronological backtracking

GRASP search template

GRASP Decision Heuristics n n Procedure decide() n Which variable to split on n What value to assign Default heuristic in GRASP: Choose the variable and assignment that directly satisfies the largest number of clauses n Other possibilities exist

GRASP Deduction n Boolean Constraint Propagation using implication graphs E. g. for the clause = (x y), if y=1, then we must have x=1 n For a variable x occuring in a clause, assignment 0 to all other literals is called antecedent assignment A(x) n E. g. for = (x y z), A(x) = {(y, 0), (z, 1)}, A(y) = {(x, 0), (z, 1)}, A(z) = {(x, 0), (y, 0)} n Variables directly responsible forcing the value of x n Antecedent assignment of a decision variable is empty

Implication Graphs n n Nodes are variable assignments x=v(x) (decision or implied) Predecessors of x are antecedent assignments A(x) n n n No predecessors for decision assignments! Special conflict vertices have A( ) = assignments to variables in the unsatisfied clause Decision level for an implied assignment is (x) = max{ (y)|(y, v(y)) A(x)}

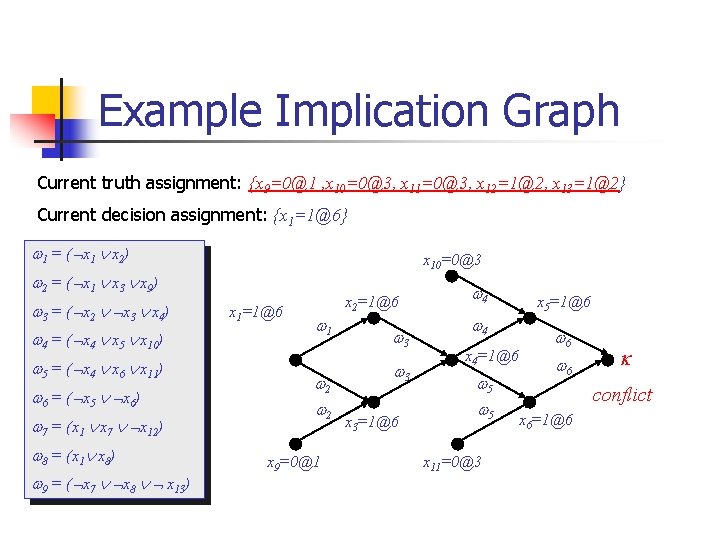
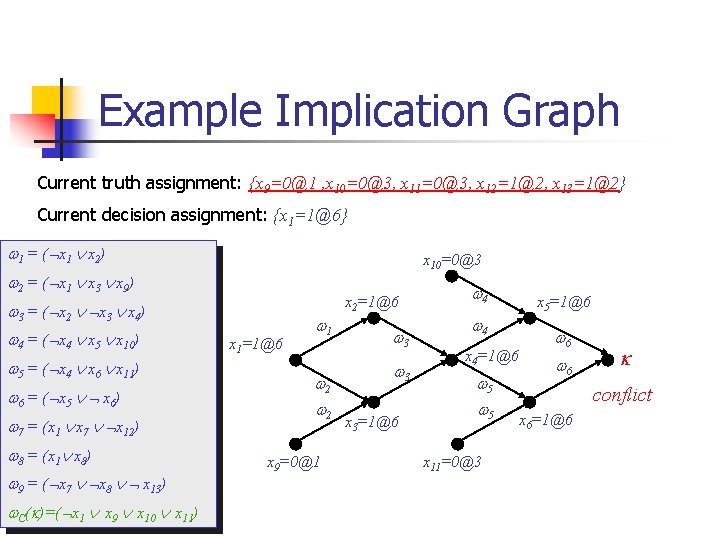
Example Implication Graph Current truth assignment: {x 9=0@1 , x 10=0@3, x 11=0@3, x 12=1@2, x 13=1@2} Current decision assignment: {x 1=1@6} 1 = ( x 1 x 2) x 10=0@3 2 = ( x 1 x 3 x 9) 3 = ( x 2 x 3 x 4) 4 = ( x 4 x 5 x 10) 5 = ( x 4 x 6 x 11) 6 = ( x 5 x 6) 7 = (x 1 x 7 x 12) 8 = (x 1 x 8) 9 = ( x 7 x 8 x 13) x 1=1@6 x 2=1@6 1 2 2 x 9=0@1 3 3 x 3=1@6 4 4 x 4=1@6 5 5 x 11=0@3 x 5=1@6 6 6 conflict x 6=1@6

GRASP Deduction Process

GRASP Conflict Analysis n n n After a conflict arises, analyze the implication graph at current decision level Add new clauses that would prevent the occurrence of the same conflict in the future Learning Determine decision level to backtrack to, might not be the immediate one Non-chronological backtracking

Learning n Determine the assignment that caused conflict n n n Backward traversal of the IG, find the roots of the IG in the transitive fanin of This assignment is necessary condition for Negation of this assignment is called conflict induced clause C( ) n Adding C( ) to the clause database will prevent the occurrence of again

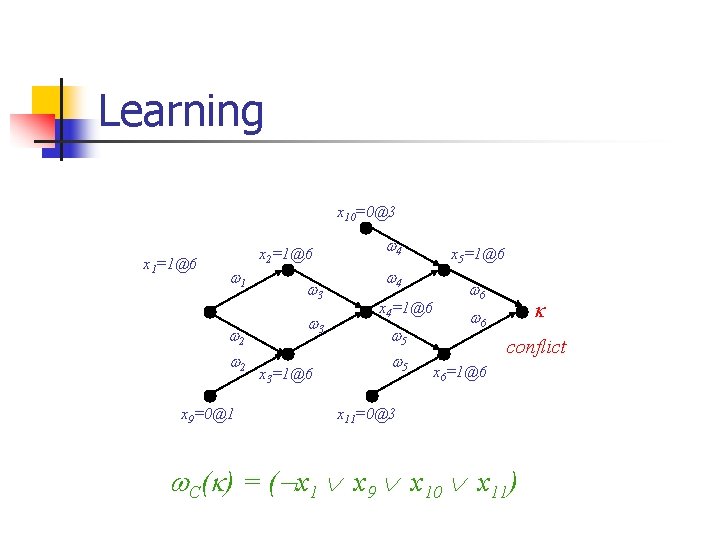
Learning x 10=0@3 x 1=1@6 x 2=1@6 1 2 2 x 9=0@1 3 3 x 3=1@6 4 4 x 4=1@6 5 5 x 5=1@6 6 6 conflict x 6=1@6 x 11=0@3 C( ) = ( x 1 x 9 x 10 x 11)

Learning n For any node of an IG x, partition A(x) into (x) = {(y, v(y)) A(x)| (y)< (x)} (x) = {(y, v(y)) A(x)| (y)= (x)} n Conflicting assignment AC( ) = causesof( ), where (x, v(x)) if A(x) = causesof(x) = (x) [ (y, v(y)) (x) causesof(y) ]o/w

Learning n n n Learning of new clauses increases clause database size Increase may be exponential Heuristically delete clauses based on a user provided parameter n If size of learned clause > parameter, don’t include it

Backtracking Failure driven assertions (FDA): n If ( ) involves current decision variable, a C n n different assignment for the current variable is immediately tried. In our IG, after erasing the assignment at level 6, C( ) becomes a unit clause x 1 This immediately implies x 1=0

Example Implication Graph Current truth assignment: {x 9=0@1 , x 10=0@3, x 11=0@3, x 12=1@2, x 13=1@2} Current decision assignment: {x 1=1@6} 1 = ( x 1 x 2) x 10=0@3 2 = ( x 1 x 3 x 9) x 2=1@6 3 = ( x 2 x 3 x 4) 4 = ( x 4 x 5 x 10) 5 = ( x 4 x 6 x 11) 6 = ( x 5 x 6) 7 = (x 1 x 7 x 12) 8 = (x 1 x 8) 9 = ( x 7 x 8 x 13) C( )=( x 1 x 9 x 10 x 11) x 1=1@6 1 2 2 x 9=0@1 3 3 x 3=1@6 4 4 x 4=1@6 5 5 x 11=0@3 x 5=1@6 6 6 conflict x 6=1@6

Example Implication Graph Current truth assignment: {x 9=0@1 , x 10=0@3, x 11=0@3, x 12=1@2, x 13=1@2} Current decision assignment: {x 1=0@6} 1 = ( x 1 x 2) 2 = ( x 1 x 3 x 9) 3 = ( x 2 x 3 x 4) 4 = ( x 4 x 5 x 10) 5 = ( x 4 x 6 x 11) 6 = ( x 5 x 6) 7 = (x 1 x 7 x 12) 8 = (x 1 x 8) 9 = ( x 7 x 8 x 13) C( ) = ( x 1 x 9 x 10 x 11) x 9=0@1 x 10=0@3 C( ) x 11=0@3 x 1=0@6

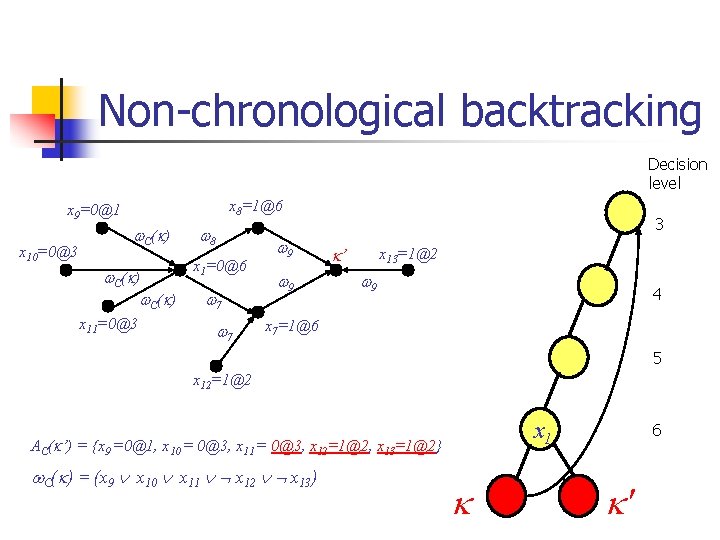
Non-chronological backtracking Decision level x 8=1@6 x 9=0@1 x 10=0@3 C( ) x 11=0@3 8 x 1=0@6 7 7 9 9 3 ’ x 13=1@2 9 4 x 7=1@6 5 x 12=1@2 x 1 AC( ’) = {x 9 =0@1, x 10 = 0@3, x 11 = 0@3, x 12=1@2, x 13=1@2} C( ) = (x 9 x 10 x 11 x 12 x 13) 6 '

Backtracking n Backtrack level is given by = max{ (x)|(x, v(x)) AC( ’)} n n = d-1 chronological backtrack < d-1 non-chronological backtrack

Procedure Diagnose()

What’s next? n Reduce overhead for constraint propagation n Better decision heuristics n Better learning, problem specific n Better engineering Chaff