GraphTheoretic Algorithm for Arbitrary Polynomial Optimization Problems with

Graph-Theoretic Algorithm for Arbitrary Polynomial Optimization Problems with Applications to Distributed Control, Power Systems, and Matrix Completion Javad Lavaei Department of Electrical Engineering Columbia University Joint work with: Ramtin Madani, Ghazal Fazelnia, Abdulrahman Kalbat and Morteza Ashraphijuo (Columbia University) Somayeh Sojoudi (NYU Langone Medical Center)

Outline v Theory: Convex relaxation v Application 1: Optimization for power networks v Application 2: Optimal decentralized control v Implementation: High-performance solver handling 1 B variables v Theory: General polynomial optimization v. Application: Matrix completion Javad Lavaei, Columbia University
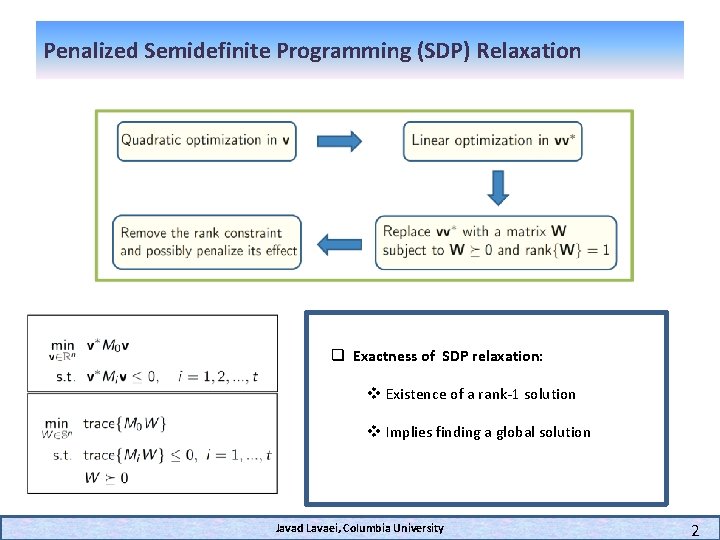
Penalized Semidefinite Programming (SDP) Relaxation q Exactness of SDP relaxation: v Existence of a rank-1 solution v Implies finding a global solution Javad Lavaei, Columbia University 2
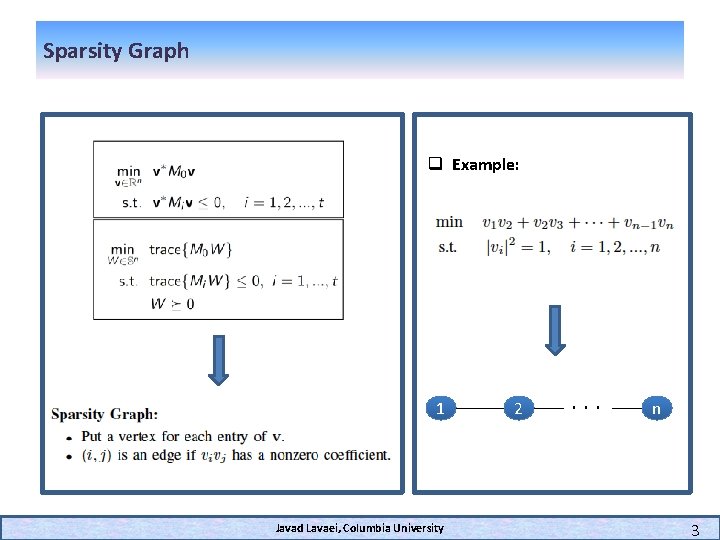
Sparsity Graph q Example: 1 Javad Lavaei, Columbia University 2 . . . n 3
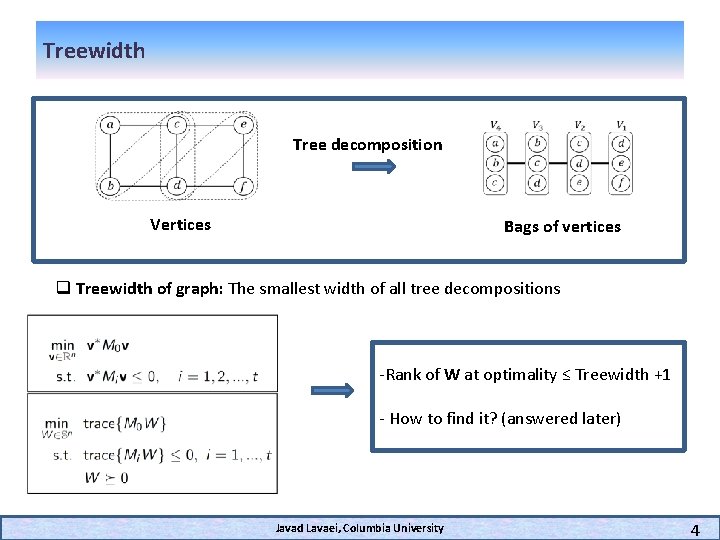
Treewidth Tree decomposition Vertices Bags of vertices q Treewidth of graph: The smallest width of all tree decompositions -Rank of W at optimality ≤ Treewidth +1 - How to find it? (answered later) Javad Lavaei, Columbia University 4

Outline v Theory: Convex relaxation v Application 1: Optimization for power networks v Application 2: Optimal decentralized control v Implementation: High-performance solver handling 1 B variables v Theory: General polynomial optimization v. Application: Matrix completion Javad Lavaei, Columbia University
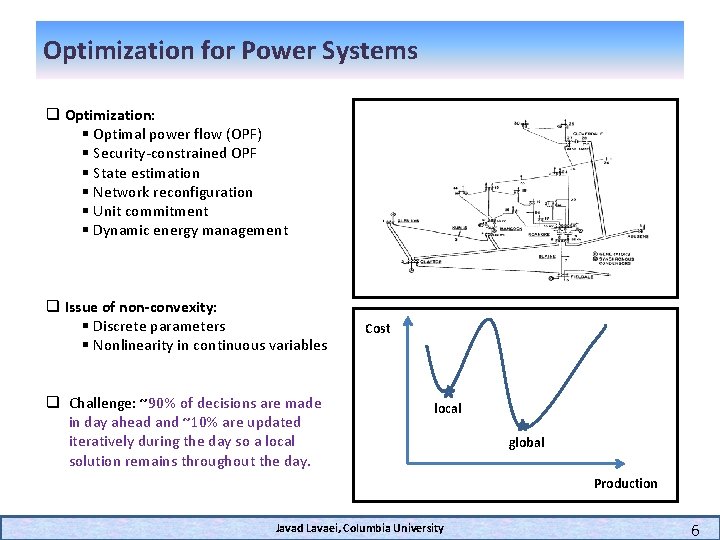
Optimization for Power Systems q Optimization: § Optimal power flow (OPF) § Security-constrained OPF § State estimation § Network reconfiguration § Unit commitment § Dynamic energy management q Issue of non-convexity: § Discrete parameters § Nonlinearity in continuous variables q Challenge: ~90% of decisions are made in day ahead and ~10% are updated iteratively during the day so a local solution remains throughout the day. Cost local global Production Javad Lavaei, Columbia University 6
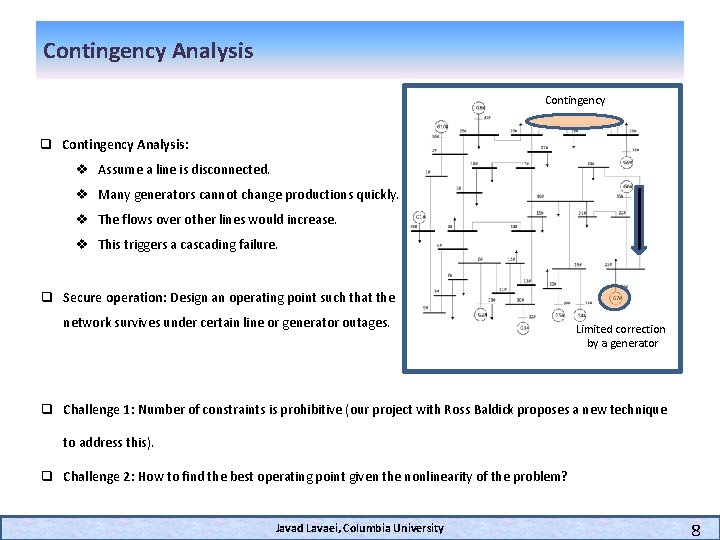
Contingency Analysis Contingency q Contingency Analysis: v Assume a line is disconnected. v Many generators cannot change productions quickly. v The flows over other lines would increase. v This triggers a cascading failure. q Secure operation: Design an operating point such that the network survives under certain line or generator outages. Limited correction by a generator q Challenge 1: Number of constraints is prohibitive (our project with Ross Baldick proposes a new technique to address this). q Challenge 2: How to find the best operating point given the nonlinearity of the problem? Javad Lavaei, Columbia University 8

Security-Constrained Optimal Power Flow (SCOPF) Cost for pre-contingency case Power flow equations for pre- and post- contingencies Physical and network limits for pre - and post- contingencies Preventive and corrective actions Javad Lavaei, Columbia University 9
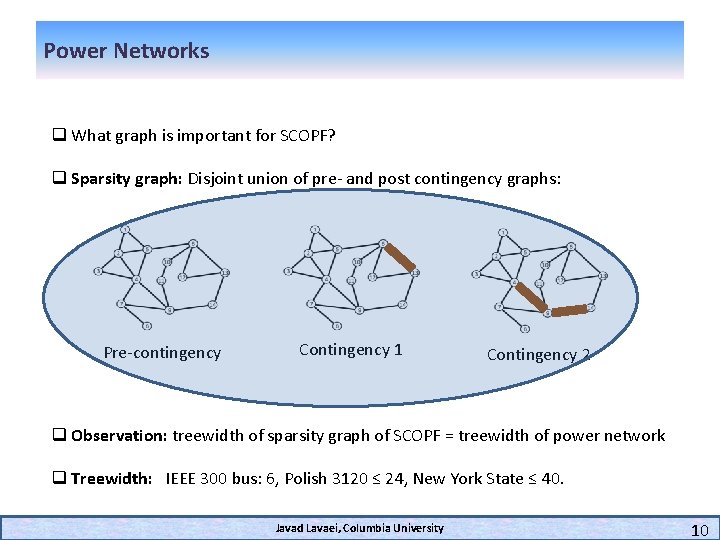
Power Networks q What graph is important for SCOPF? q Sparsity graph: Disjoint union of pre- and post contingency graphs: Pre-contingency Contingency 1 Contingency 2 q Observation: treewidth of sparsity graph of SCOPF = treewidth of power network q Treewidth: IEEE 300 bus: 6, Polish 3120 ≤ 24, New York State ≤ 40. Javad Lavaei, Columbia University 10
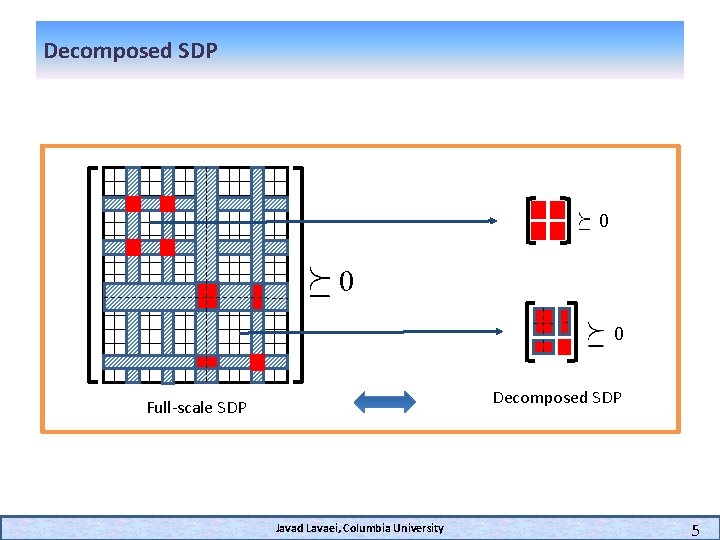
Decomposed SDP 0 0 0 Decomposed SDP Full-scale SDP Javad Lavaei, Columbia University 5

Power Networks q Decomposed relaxed SCOPF: SDP problem with small-sized constraints 0, 0 q Reduction of the number of variables for a Polish system from ~9, 000 to ~90 K. q Result: Rank of W at optimality ≤ Treewidth +1 q Stronger Result: Rank of W at optimality ≤ maximum rank of bags q By-product: Lines of network in not-rank-1 bags make SDP fail. q Penalized SDP: Penalize the loss over problematic lines Javad Lavaei, Columbia University 11
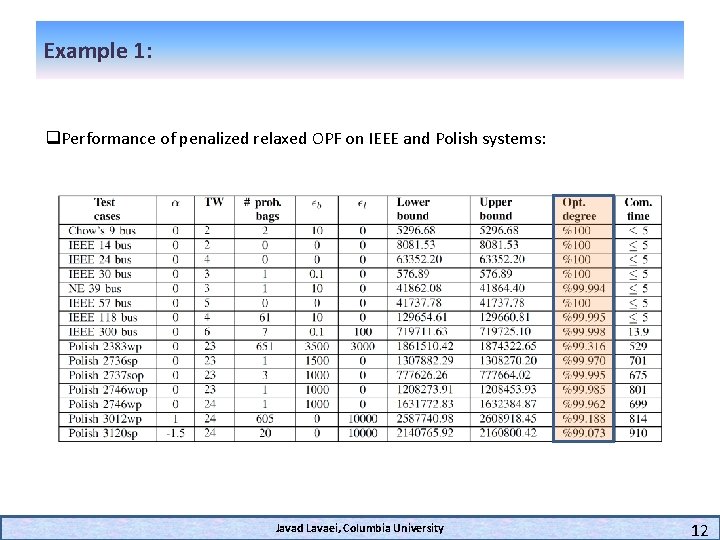
Example 1: q. Performance of penalized relaxed OPF on IEEE and Polish systems: Javad Lavaei, Columbia University 12
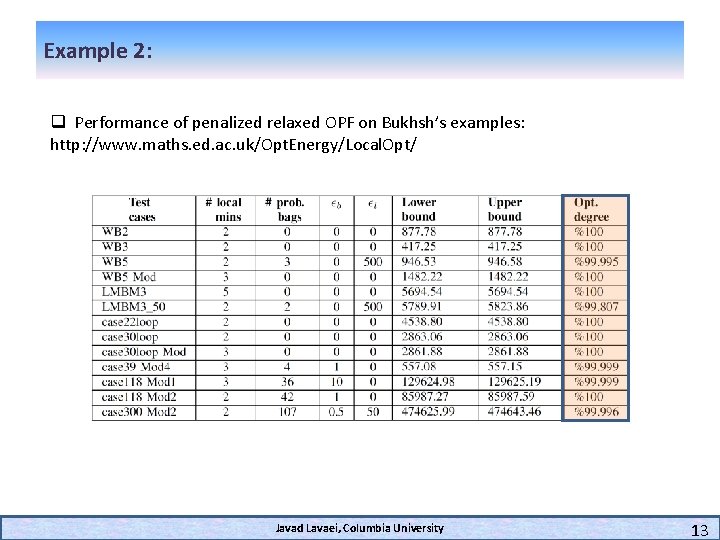
Example 2: q Performance of penalized relaxed OPF on Bukhsh’s examples: http: //www. maths. ed. ac. uk/Opt. Energy/Local. Opt/ Javad Lavaei, Columbia University 13
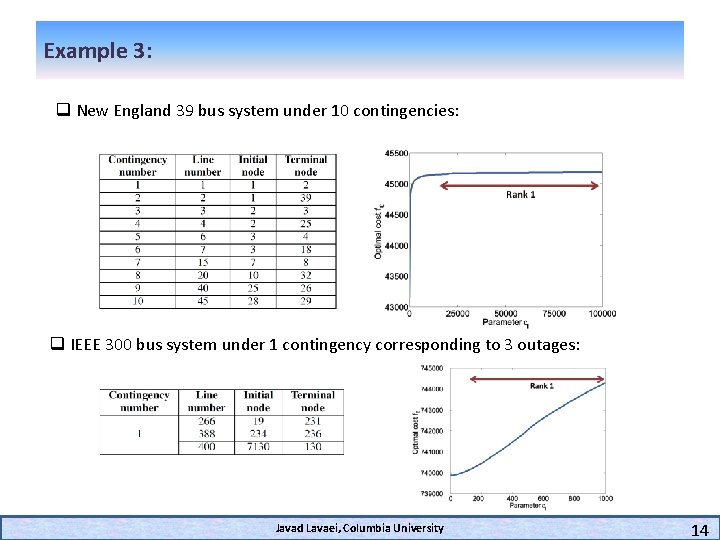
Example 3: q New England 39 bus system under 10 contingencies: q IEEE 300 bus system under 1 contingency corresponding to 3 outages: Javad Lavaei, Columbia University 14

Outline v Theory: Convex relaxation v Application 1: Optimization for power networks v Application 2: Optimal decentralized control v Implementation: High-performance solver handling 1 B variables v Theory: General polynomial optimization v. Application: Matrix completion Javad Lavaei, Columbia University

Motivation q Computational challenges arising in the control of real-world systems: v Communication networks v Electrical power systems v Aerospace systems v Large-space flexible structures v Traffic systems v Wireless sensor networks v Various multi-agent systems q Decentralized controller: v A group of isolated local controllers q Distributed controller: v Partially interacting local controllers Javad Lavaei, Columbia University 15

Optimal Distributed control (ODC) q Stochastic ODC: Find a structured control for the system: disturbance noise to minimize the cost functional: q Finite-horizon ODC: Deterministic system with the objective: q Infinite-horizon ODC: Terminal time equal to infinity. Javad Lavaei, Columbia University 16
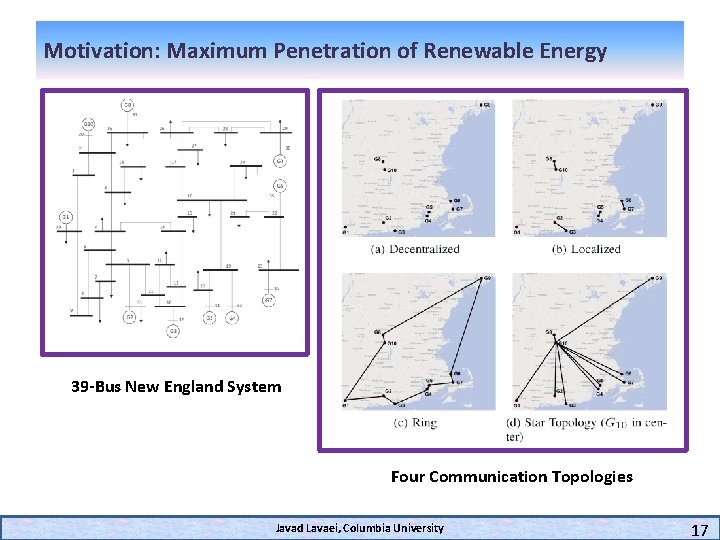
Motivation: Maximum Penetration of Renewable Energy 39 -Bus New England System Four Communication Topologies Javad Lavaei, Columbia University 17
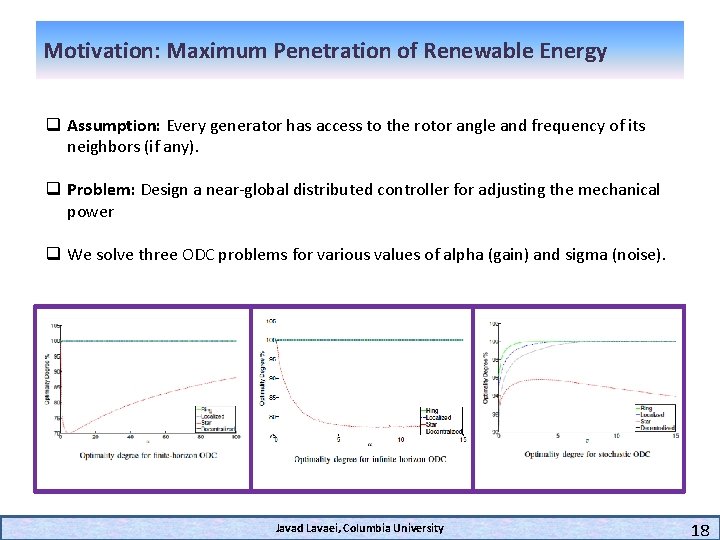
Motivation: Maximum Penetration of Renewable Energy q Assumption: Every generator has access to the rotor angle and frequency of its neighbors (if any). q Problem: Design a near-global distributed controller for adjusting the mechanical power q We solve three ODC problems for various values of alpha (gain) and sigma (noise). Javad Lavaei, Columbia University 18
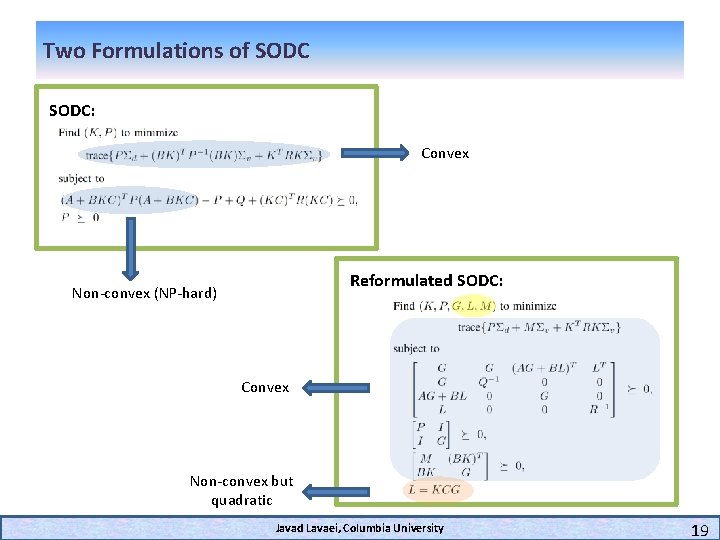
Two Formulations of SODC: Convex Reformulated SODC: Non-convex (NP-hard) Convex Non-convex but quadratic Javad Lavaei, Columbia University 19

Quadratic Formulation in Static Case q SDP relaxation for SODC: W q Theorem: W has rank 1, 2, or 3 at optimality for finite-horizon ODC, infinite-horizon ODC, and SODC. Lyapunov domain Time domain Javad Lavaei, Columbia University 20

Computationally-Cheap SDP Relaxation q Dimension of SDP variable = O(n 2) q Is lower bound tight enough? q Can penalize the trace of W in the objective to make it penalized SDP. q Goal: Design a new SDP relaxation such that: v Dimension of SDP variable = O(n) v The entries of W are automatically penalized in the problem. Javad Lavaei, Columbia University 21
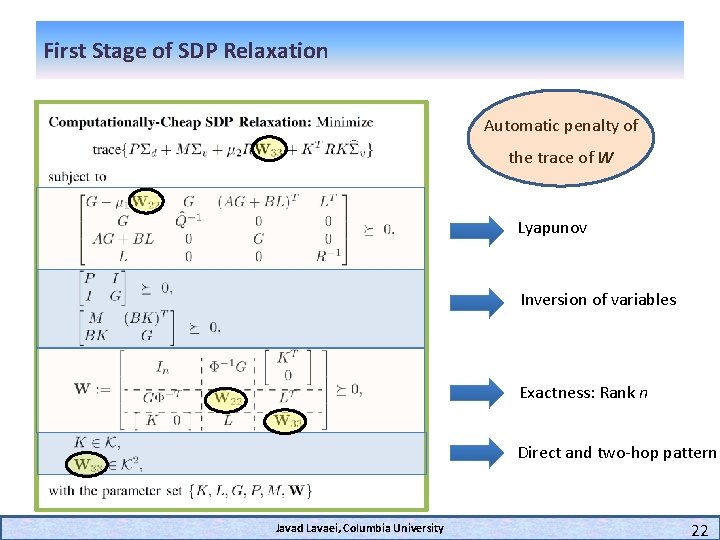
First Stage of SDP Relaxation Automatic penalty of the trace of W Lyapunov Inversion of variables Exactness: Rank n Direct and two-hop pattern Javad Lavaei, Columbia University 22

Two-Stage SDP Relaxation q Stage 1: Solve SDP relaxation. q Stage 2: Recover a near-global controller. q Direct Method: Read off the controller from the SDP solution. q Indirect Method: Read off G from the SDP solution and solve a convex program. q ϒ helps to make the problem feasible, but it’s penalized to keep its value low. Javad Lavaei, Columbia University 23
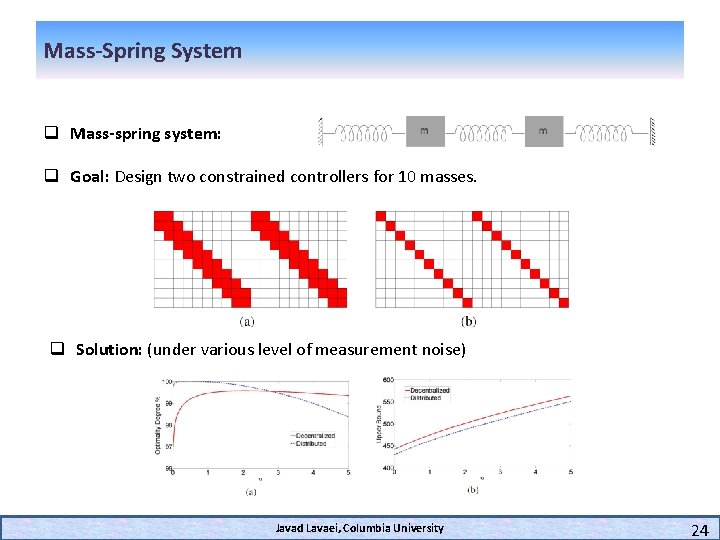
Mass-Spring System q Mass-spring system: q Goal: Design two constrained controllers for 10 masses. q Solution: (under various level of measurement noise) Javad Lavaei, Columbia University 24

Outline v Theory: Convex relaxation v Application 1: Optimization for power networks v Application 2: Optimal decentralized control v Implementation: High-performance solver handling 1 B variables v Theory: General polynomial optimization v. Application: Matrix completion Javad Lavaei, Columbia University
Low-Complex Algorithm for Sparse SDP Slides for this section are removed. Javad Lavaei, Columbia University 25

Outline v Theory: Convex relaxation v Application 1: Optimization for power networks v Application 2: Optimal decentralized control v Implementation: High-performance solver handling 1 B variables v Theory: General polynomial optimization v. Application: Matrix completion Javad Lavaei, Columbia University

Polynomial Optimization q Vertex Duplication Procedure: q Edge Elimination Procedure: q This gives rise to a sparse QCQP with a sparse graph. q The treewidth can be reduced to 1. Theorem: Every polynomial optimization has a QCQP formulation whose SDP relaxation has a solution with rank 1 or 2. Javad Lavaei, Columbia University 28

Outline v Theory: Convex relaxation v Application 1: Optimization for power networks v Application 2: Optimal decentralized control v Implementation: High-performance solver handling 1 B variables v Theory: General polynomial optimization v. Application: Matrix completion Javad Lavaei, Columbia University
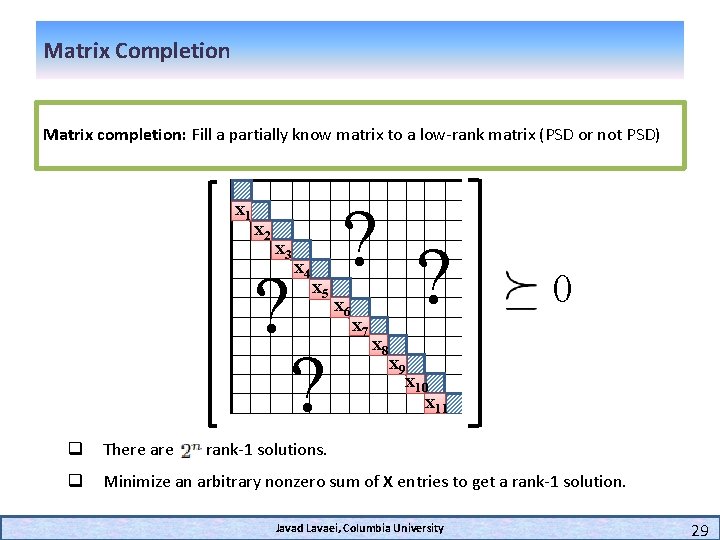
Matrix Completion Matrix completion: Fill a partially know matrix to a low-rank matrix (PSD or not PSD) x 1 ? ? x 2 x 3 x 4 x 5 x 6 x 7 x 8 0 x 9 x 10 x 11 q There are rank-1 solutions. q Minimize an arbitrary nonzero sum of X entries to get a rank-1 solution. Javad Lavaei, Columbia University 29
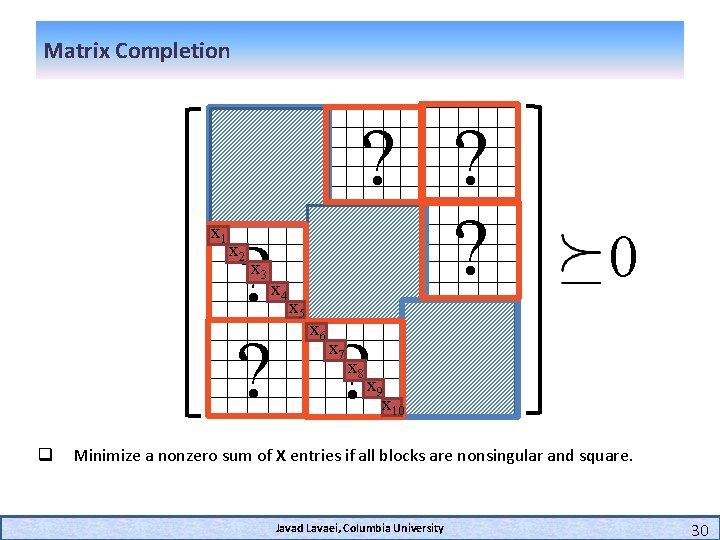
Matrix Completion x 1 q ? ? ? x 2 x 3 x 4 x 5 x 6 x 7 x 8 0 x 9 x 10 Minimize a nonzero sum of X entries if all blocks are nonsingular and square. Javad Lavaei, Columbia University 30
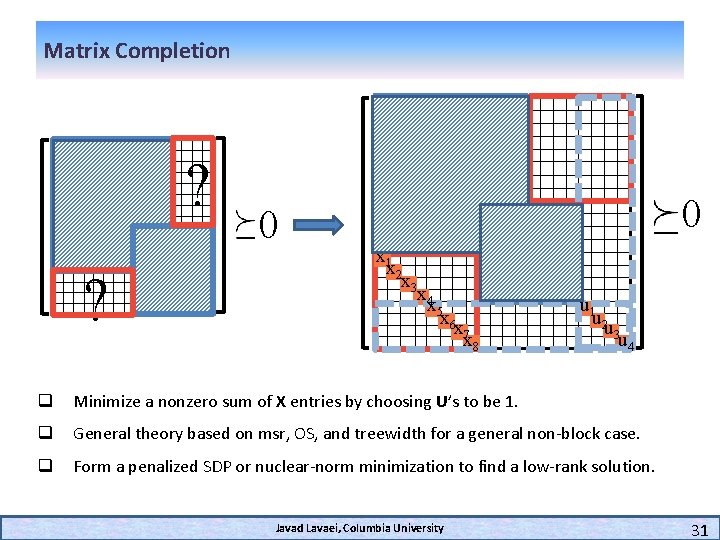
Matrix Completion ? ? 0 0 x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 u 1 u 2 u 3 u 4 q Minimize a nonzero sum of X entries by choosing U’s to be 1. q General theory based on msr, OS, and treewidth for a general non-block case. q Form a penalized SDP or nuclear-norm minimization to find a low-rank solution. Javad Lavaei, Columbia University 31

Conclusions v Theory: Low-rank optimization v Applications: Power, Control, nonlinear optimization, … v Implementation: High-performance solver handling 1 B variables v Two of our solvers posted online and another one is forthcoming. v Collaboration with industry for demonstration on real data. Javad Lavaei, Columbia University 32
- Slides: 35