GRAPHS TYPES OF EQUATIONS STRAIGHT LINE GRAPHS NO

STRAIGHT LINE GRAPHS ( NO TURNING POINT)

CUBIC GRAPH • The y intercept is still the point where the graph hits

INTERSECTING GRAPHS • Consider the graphs of y =x^2 + x -2 and y

INTERSECTING GRAPHS • Sometimes you can be asked for a range. • Example: Give

INTERSECTING GRAPHS • You might also be asked to find the range of x

INTERSECTING GRAPHS • When a cubic graph intersects a straight line graph, you may

INTERSECTING GRAPHS • Give the range of values such that the cubic < straight

EQUATIONS OF INTERSECTING GRAPHS • You have been asked to plot the graph of

INTERSECTING GRAPHS • First, take the new equation and write it down. • x^2

Slides: 19

Download presentation

GRAPHS

TYPES OF EQUATIONS •

STRAIGHT LINE GRAPHS ( NO TURNING POINT)

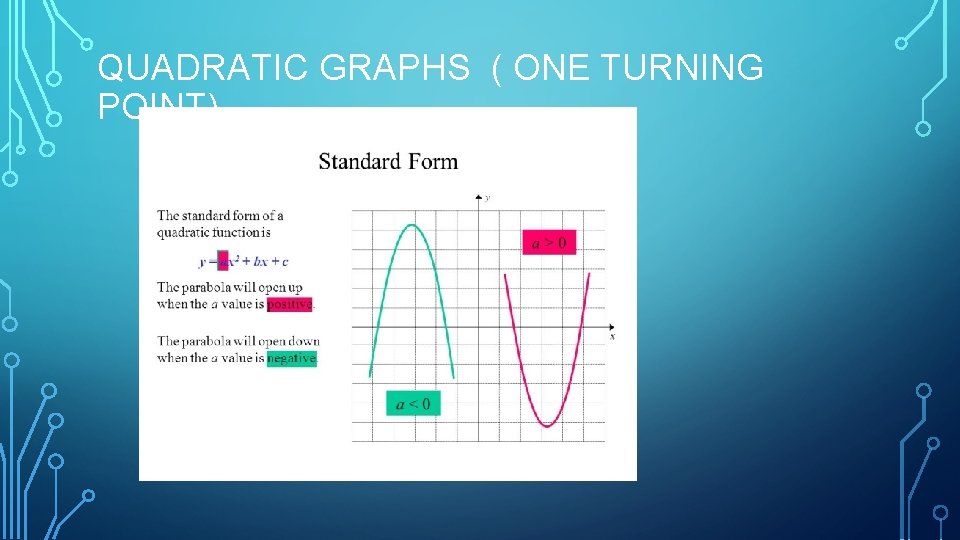
QUADRATIC GRAPHS ( ONE TURNING POINT)

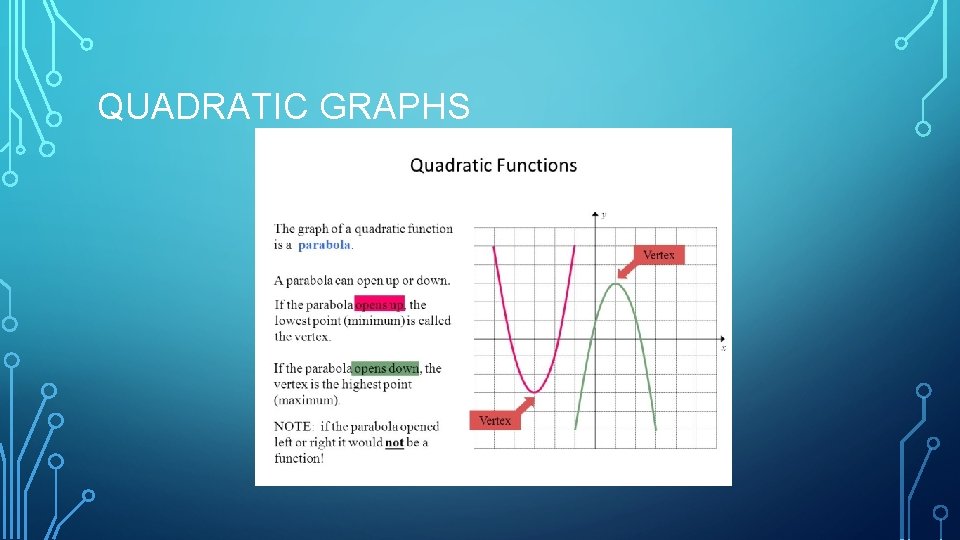
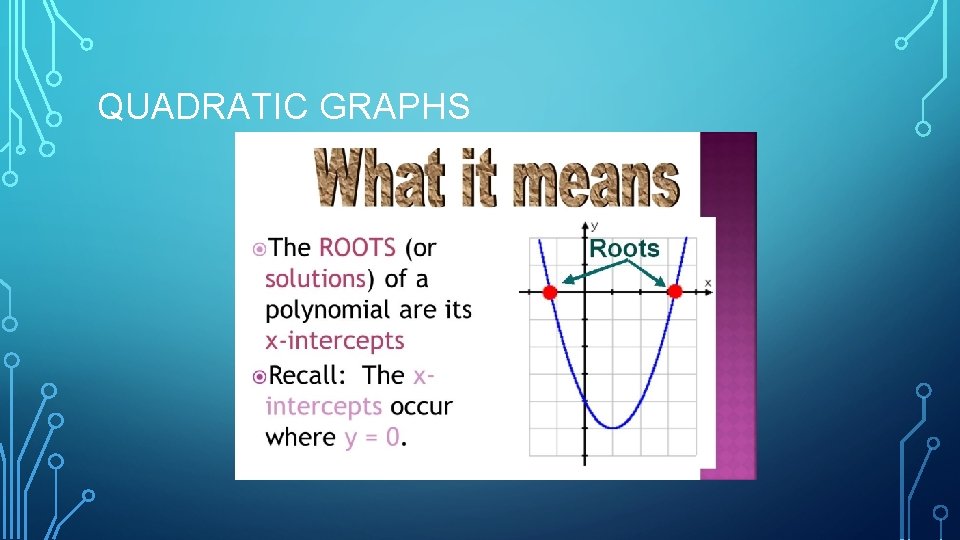
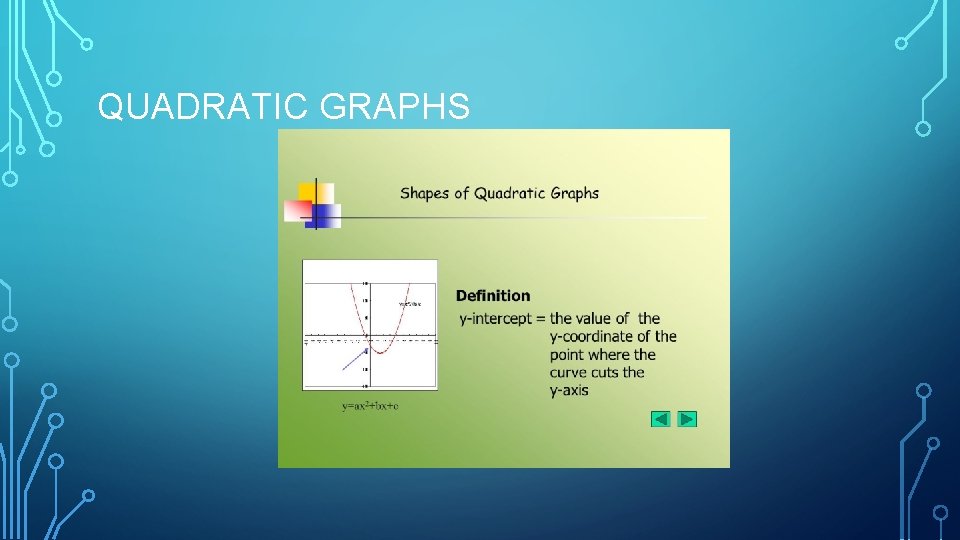
QUADRATIC GRAPHS

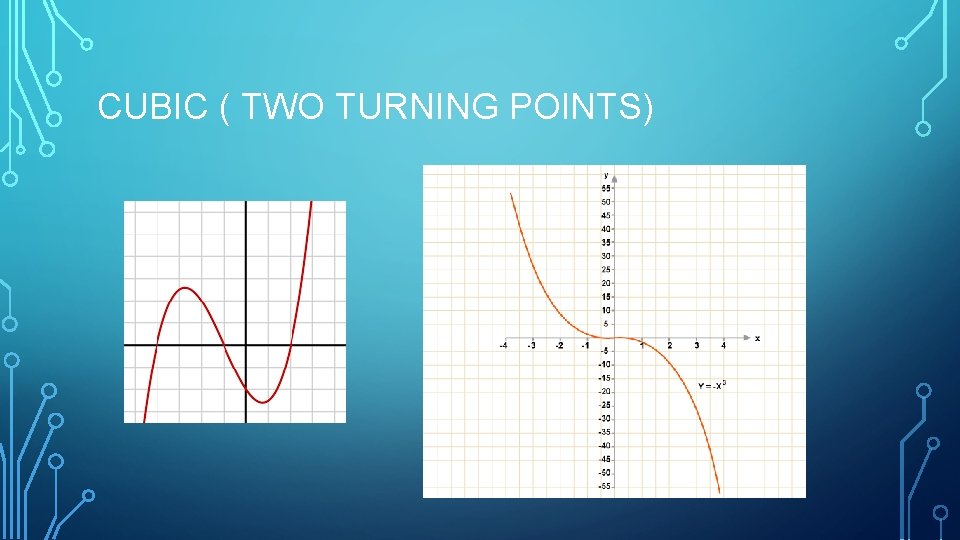
CUBIC ( TWO TURNING POINTS)

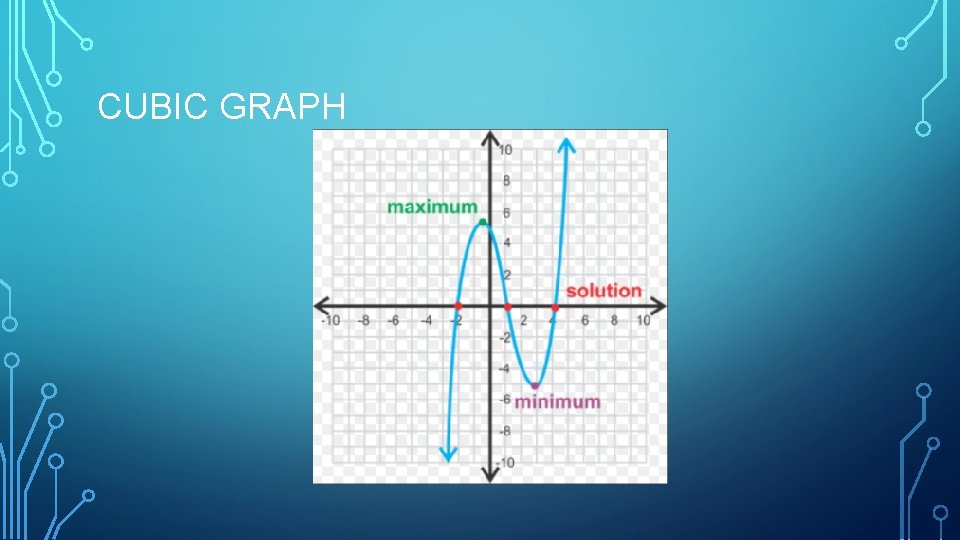
CUBIC GRAPH

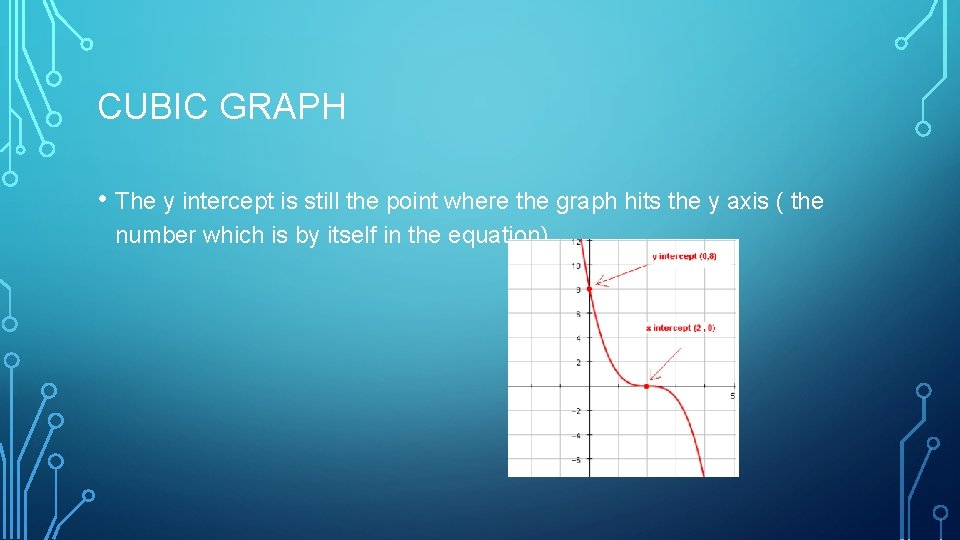
CUBIC GRAPH • The y intercept is still the point where the graph hits the y axis ( the number which is by itself in the equation)

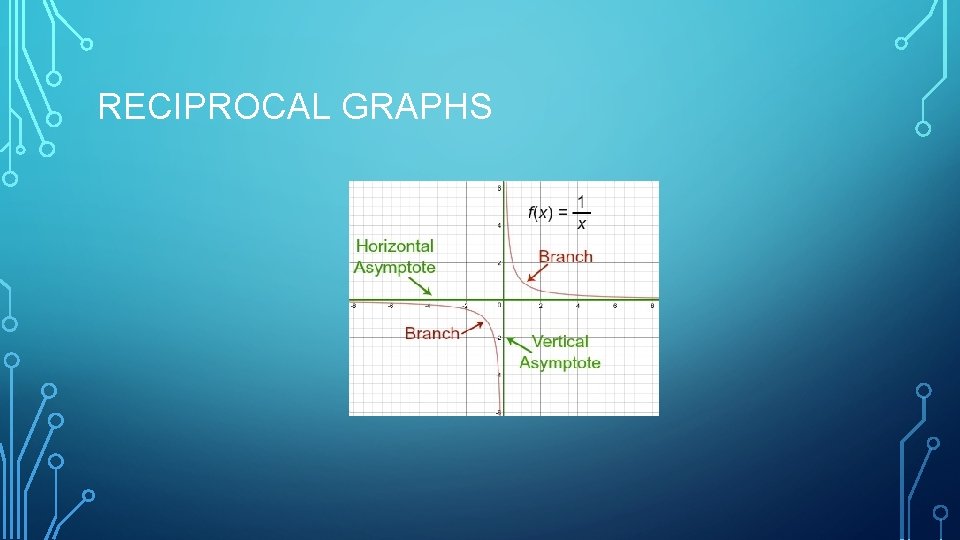
RECIPROCAL GRAPHS

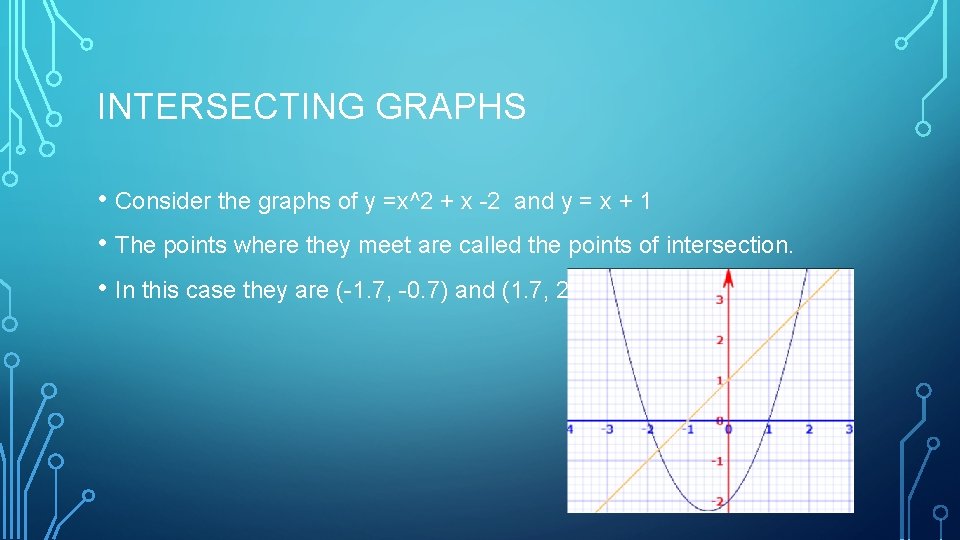
INTERSECTING GRAPHS • Consider the graphs of y =x^2 + x -2 and y = x + 1 • The points where they meet are called the points of intersection. • In this case they are (-1. 7, -0. 7) and (1. 7, 2. 7)

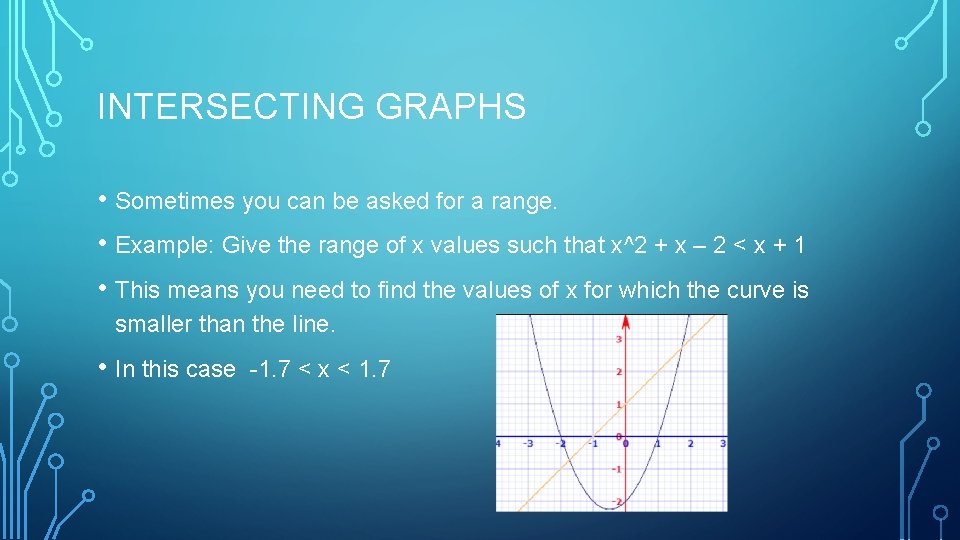
INTERSECTING GRAPHS • Sometimes you can be asked for a range. • Example: Give the range of x values such that x^2 + x – 2 < x + 1 • This means you need to find the values of x for which the curve is smaller than the line. • In this case -1. 7 < x < 1. 7

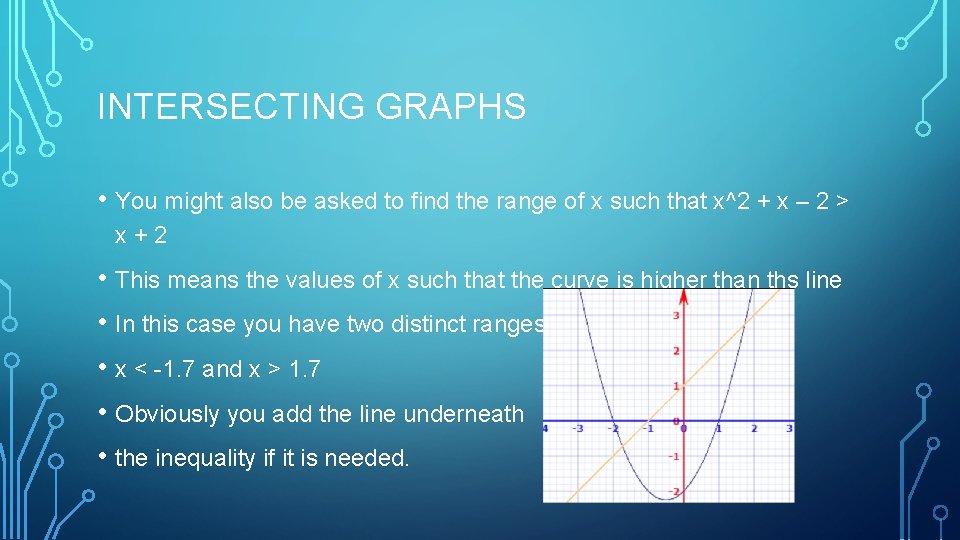
INTERSECTING GRAPHS • You might also be asked to find the range of x such that x^2 + x – 2 > x+2 • This means the values of x such that the curve is higher than ths line • In this case you have two distinct ranges • x < -1. 7 and x > 1. 7 • Obviously you add the line underneath • the inequality if it is needed.

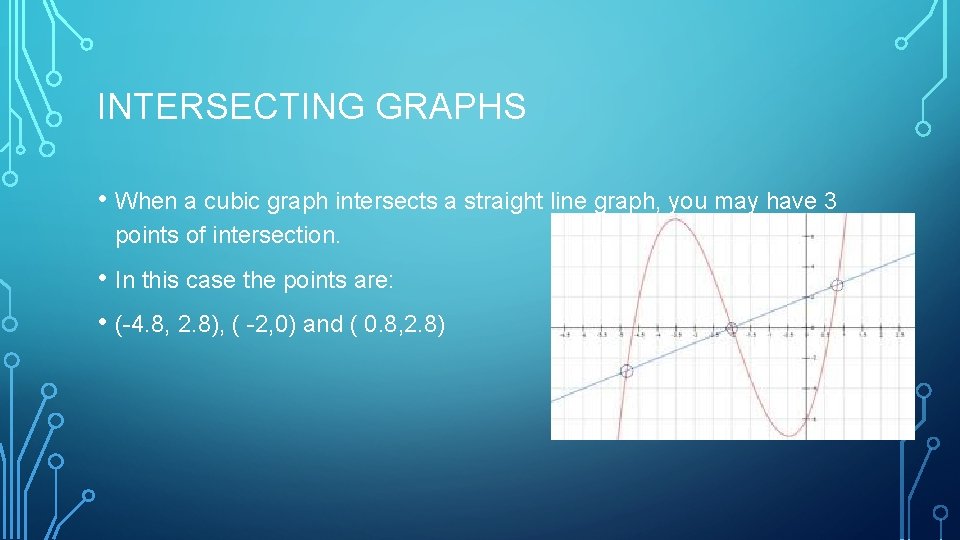
INTERSECTING GRAPHS • When a cubic graph intersects a straight line graph, you may have 3 points of intersection. • In this case the points are: • (-4. 8, 2. 8), ( -2, 0) and ( 0. 8, 2. 8)

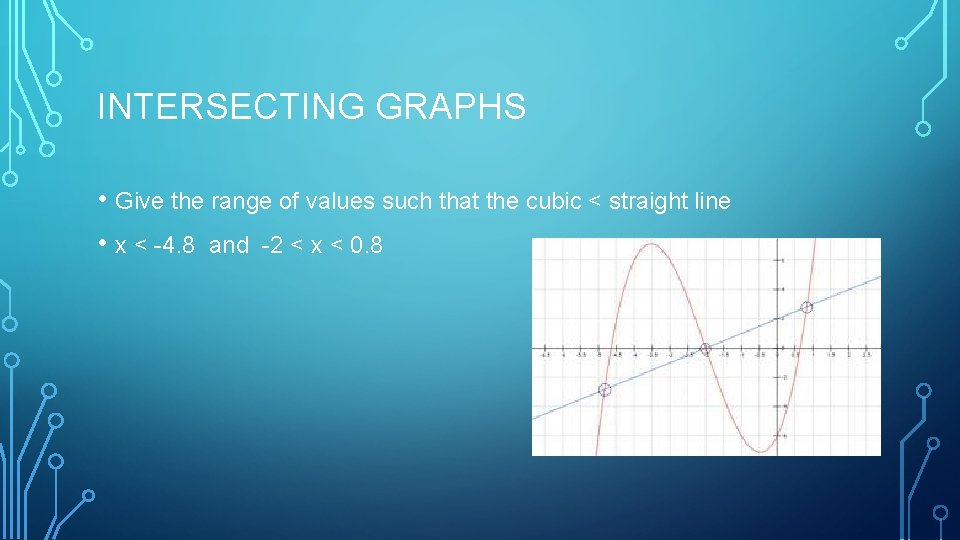
INTERSECTING GRAPHS • Give the range of values such that the cubic < straight line • x < -4. 8 and -2 < x < 0. 8

EQUATIONS OF INTERSECTING GRAPHS • You have been asked to plot the graph of y = x^2 + 2 x -3. • Then you are asked • “ By plotting a suitable graph, solve the equation x^2 + x – 1 = 0” • You need to get the new equation to resemble the old one.

INTERSECTING GRAPHS • First, take the new equation and write it down. • x^2 + x – 1 = 0 Then, take whatever is different from the old one to the other side. x^2 = -x + 1 Then, add the terms which will make it like the old one x^2 + 2 x – 3 = -x + 1 +2 x – 3 x^2 + 2 x – 3 = x – 2 Make sure that you put them on both sides Simplify and plot the equation on the right. The solution will be the x values of the points of intersection of the two graphs.