GRAPHS THEROY Graphs Graph basics and definitions n

GRAPHS THEROY

–Graphs Graph basics and definitions n n Vertices/nodes, edges, adjacency, incidence Degree, in-degree, out-degree Subgraphs, unions, isomorphism Adjacency matrices Types of Graphs n n Trees Undirected graphs w n n n Simple graphs, Multigraphs, Pseudographs Digraphs, Directed multigraph Bipartite Complete graphs, cycles, wheels, cubes, complete bipartite 2

Graphs –Notion A graph is a bunch of vertices (or nodes) represented by circles which are connected by edges, represented by line segments. Mathematically, graphs are binary-relations on their vertex set (except for multigraphs). In Data Structures one often starts with trees and generalizes to graphs. In this course, opposite approach: We start with graphs and restrict to get trees. 3

Graphs: Basic Definitions A graph, G, comprises a set V of vertices and a set E of edges. The vertex set can be anything, but is most commonly a collection of letters or numbers. The set of edges is a set of doubleton subsets of V. That is E⊆{{a, b}: a, b∈V and a≠b}. We denote the graph by G(V, E). If G(V, E) is a graph and {a, b}∈E, then we say vertices a and b are adjacent and the edge {a, b} joins them or connects them or is incident on them. We call a and b the endpoints of the edge. Two edges that share one vertex, such as {a, b} and {b, c} with a≠c, are adjacent to each other. 4

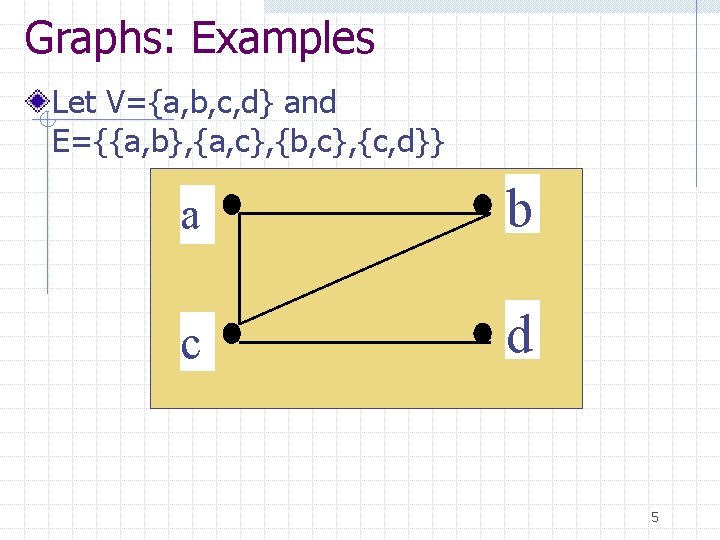
Graphs: Examples Let V={a, b, c, d} and E={{a, b}, {a, c}, {b, c}, {c, d}} a b c d 5

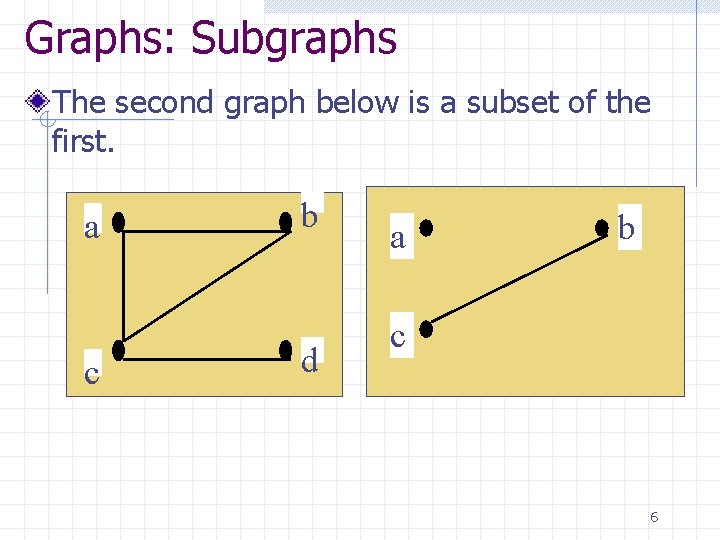
Graphs: Subgraphs The second graph below is a subset of the first. a c b d a b c 6

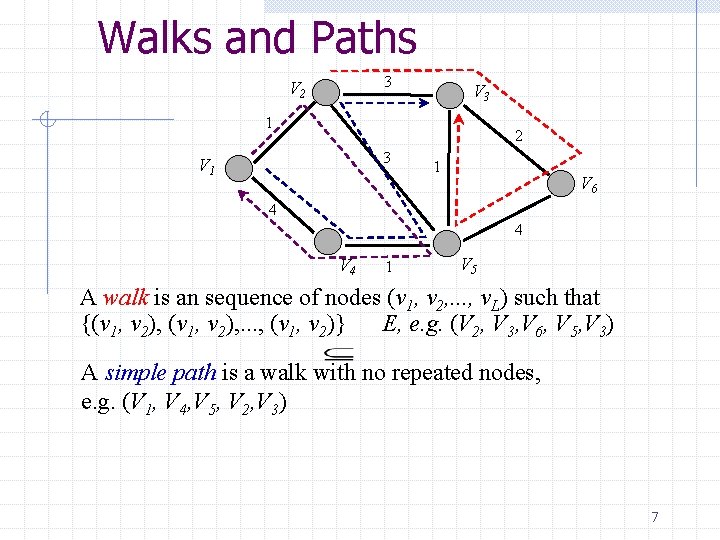
Walks and Paths 3 V 2 V 3 1 2 3 V 1 1 V 6 4 4 V 4 1 V 5 A walk is an sequence of nodes (v 1, v 2, . . . , v. L) such that {(v 1, v 2), . . . , (v 1, v 2)} E, e. g. (V 2, V 3, V 6, V 5, V 3) A simple path is a walk with no repeated nodes, e. g. (V 1, V 4, V 5, V 2, V 3) 7

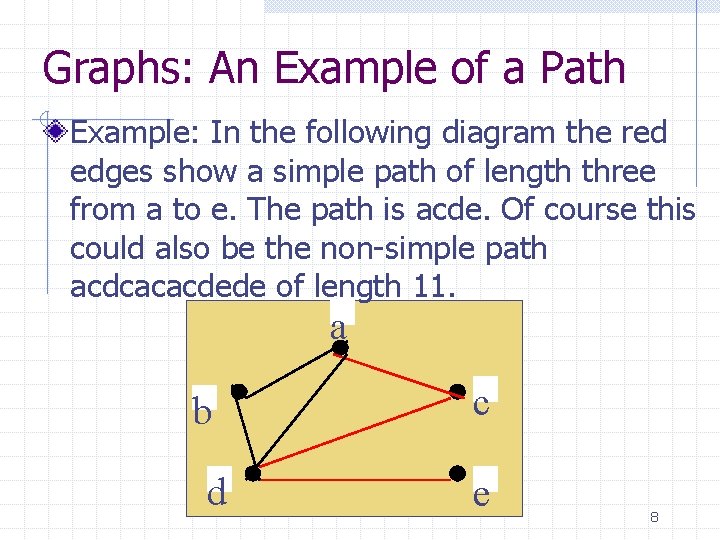
Graphs: An Example of a Path Example: In the following diagram the red edges show a simple path of length three from a to e. The path is acde. Of course this could also be the non-simple path acdcacacdede of length 11. a b d c e 8

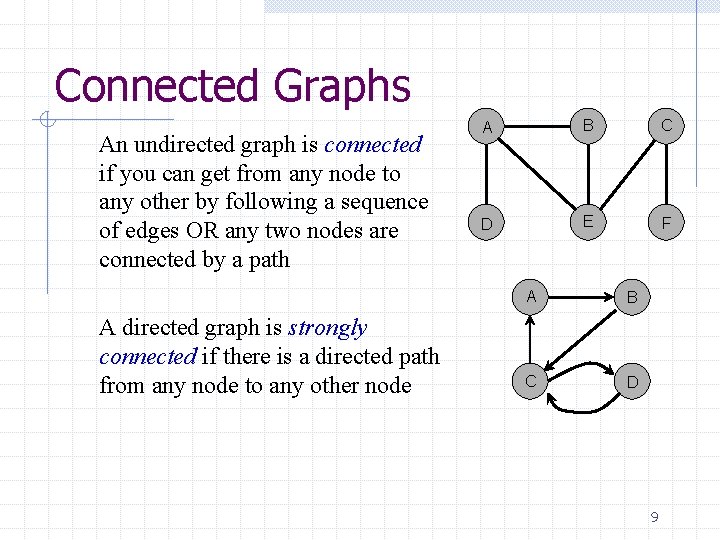
Connected Graphs An undirected graph is connected if you can get from any node to any other by following a sequence of edges OR any two nodes are connected by a path A directed graph is strongly connected if there is a directed path from any node to any other node A B C D E F A B C D 9

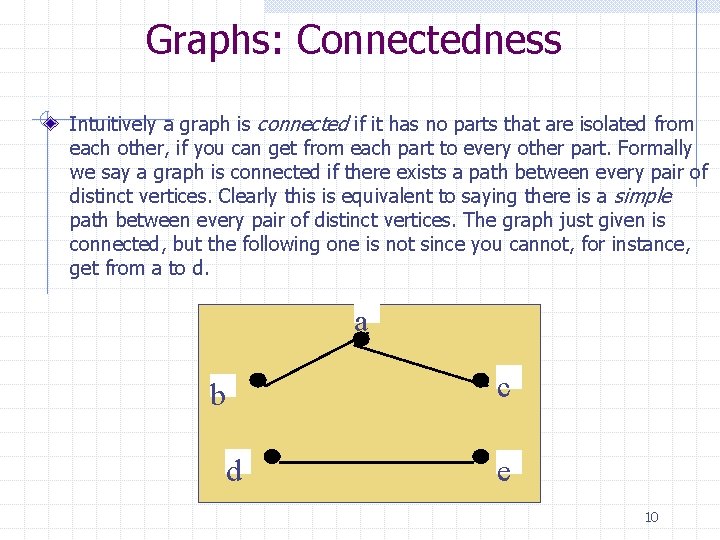
Graphs: Connectedness Intuitively a graph is connected if it has no parts that are isolated from each other, if you can get from each part to every other part. Formally we say a graph is connected if there exists a path between every pair of distinct vertices. Clearly this is equivalent to saying there is a simple path between every pair of distinct vertices. The graph just given is connected, but the following one is not since you cannot, for instance, get from a to d. a b d c e 10

Trees A very important type of graph in CS is called a tree: Real Tree 11

Trees A very important type of graph in CS is called a tree: Real Tree transformation 12

Trees A very important type of graph in CS is called a tree: Real Tree transformation 13

Trees A very important type of graph in CS is called a tree: Real Tree transformation Abstract Tree 14

Simple Graphs Different purposes require different types of graphs. EG: Suppose a local computer network n n n Is bidirectional (undirected) Has no loops (no “self-communication”) Has unique connections between computers Sensible to represent as follows: 15

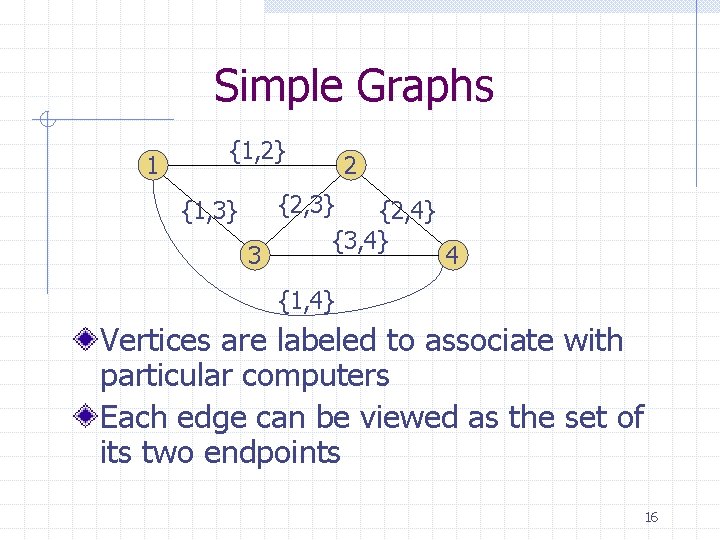
Simple Graphs 1 {1, 2} {1, 3} 3 2 {2, 3} {2, 4} {3, 4} 4 {1, 4} Vertices are labeled to associate with particular computers Each edge can be viewed as the set of its two endpoints 16

Simple Graphs DEF: A simple graph G = (V, E ) consists of a non-empty set V of vertices (or nodes) and a set E (possibly empty) of edges where each edge is a subset of V with cardinality 2 (an unordered pair). Q: For a set V with n elements, how many possible edges there? 17

Simple Graphs A: The number of pairs in V = n · (n -1) / 2 Q: How many possible graphs are there for the same set of vertices V ? 18

Simple Graphs A: The number of subsets in the set of possible edges. There are n · (n -1) / 2 possible edges, therefore the number of graphs on V is 2 n(n -1)/2 19

Multigraphs If computers are connected via internet instead of directly, there may be several routes to choose from for each connection. Depending on traffic, one route could be better than another. Makes sense to allow multiple edges, but still no self-loops: 20

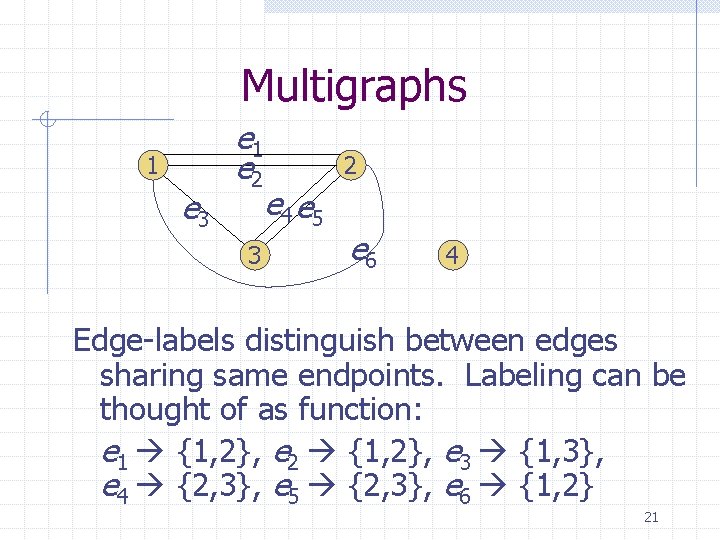
Multigraphs 1 e 3 e 1 e 2 3 2 e 4 e 5 e 6 4 Edge-labels distinguish between edges sharing same endpoints. Labeling can be thought of as function: e 1 {1, 2}, e 2 {1, 2}, e 3 {1, 3}, e 4 {2, 3}, e 5 {2, 3}, e 6 {1, 2} 21

Multigraphs DEF: A multigraph G = (V, E, f ) consists of a non-empty set V of vertices (or nodes), a set E (possibly empty) of edges and a function f with domain E and codomain the set of pairs in V. 22

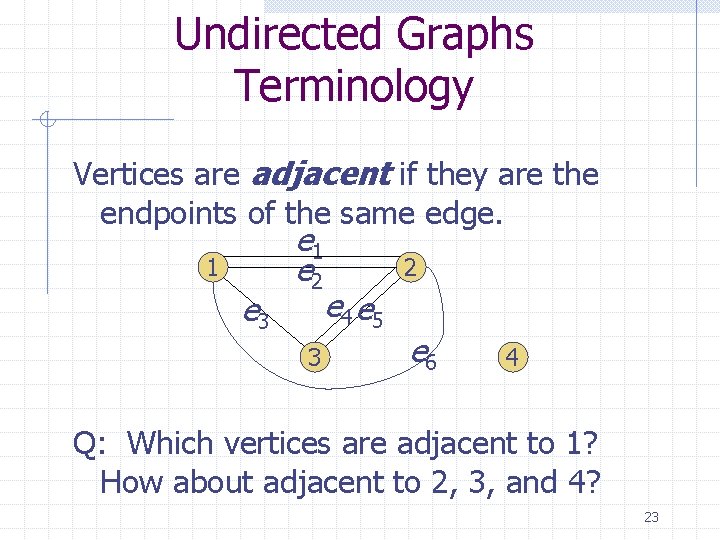
Undirected Graphs Terminology Vertices are adjacent if they are the endpoints of the same edge. 1 e 3 e 1 e 2 3 2 e 4 e 5 e 6 4 Q: Which vertices are adjacent to 1? How about adjacent to 2, 3, and 4? 23

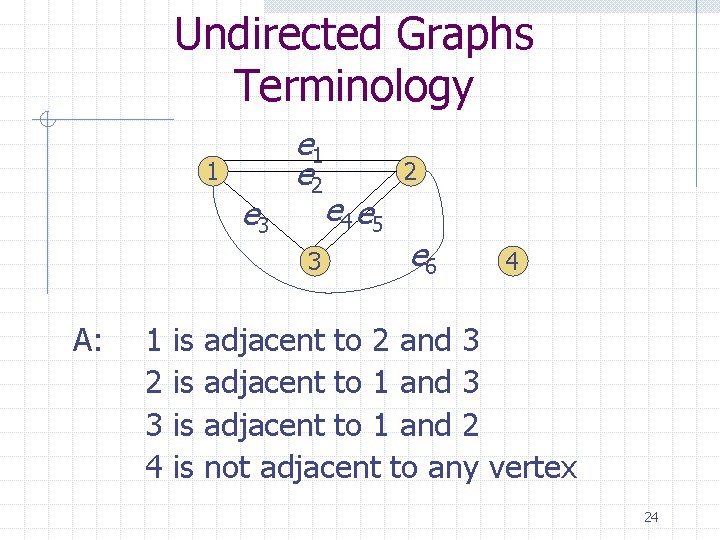
Undirected Graphs Terminology 1 e 3 e 1 e 2 3 A: 1 2 3 4 is is 2 e 4 e 5 e 6 4 adjacent to 2 and 3 adjacent to 1 and 2 not adjacent to any vertex 24

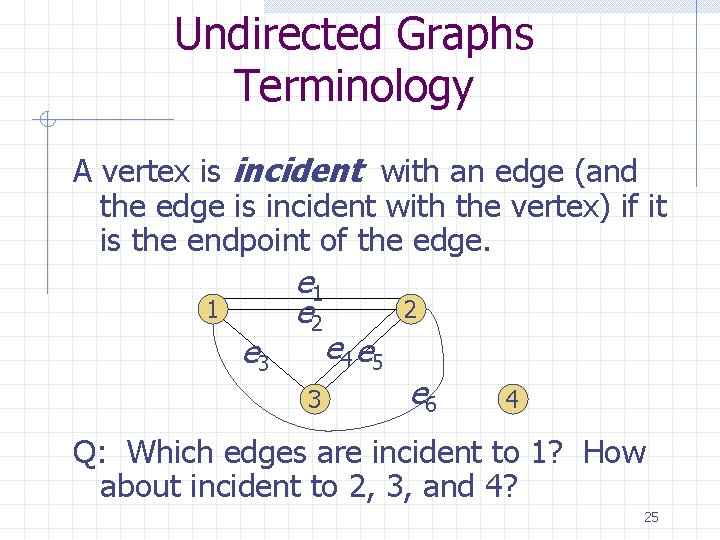
Undirected Graphs Terminology A vertex is incident with an edge (and the edge is incident with the vertex) if it is the endpoint of the edge. 1 e 3 e 1 e 2 3 2 e 4 e 5 e 6 4 Q: Which edges are incident to 1? How about incident to 2, 3, and 4? 25

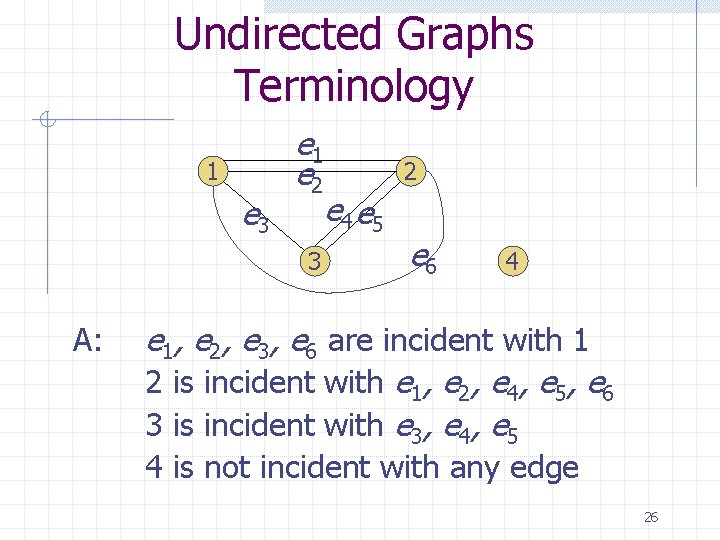
Undirected Graphs Terminology 1 e 3 e 1 e 2 3 A: 2 e 4 e 5 e 6 4 e 1, e 2, e 3, e 6 are incident with 1 2 is incident with e 1, e 2, e 4, e 5, e 6 3 is incident with e 3, e 4, e 5 4 is not incident with any edge 26

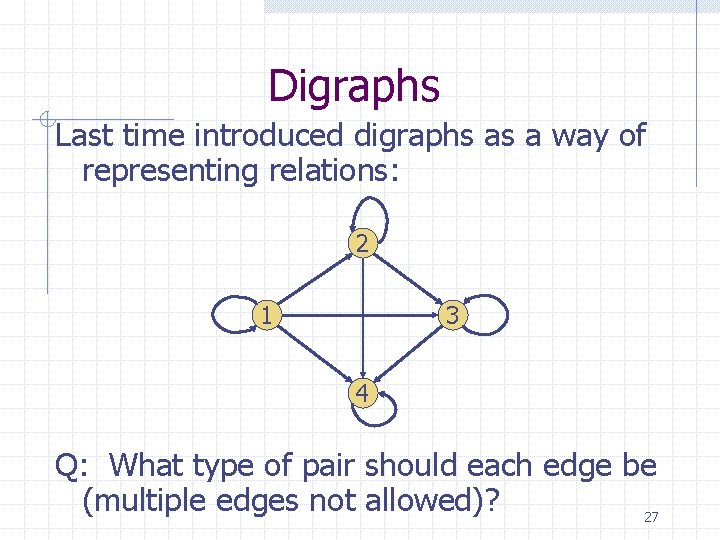
Digraphs Last time introduced digraphs as a way of representing relations: 2 1 3 4 Q: What type of pair should each edge be (multiple edges not allowed)? 27

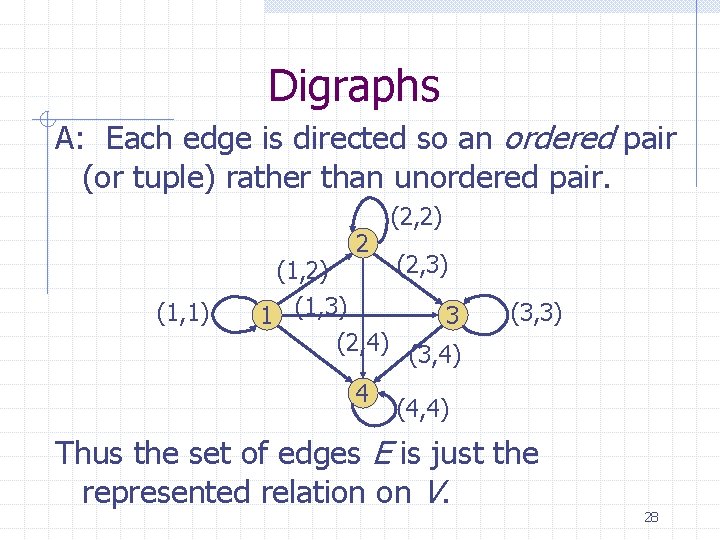
Digraphs A: Each edge is directed so an ordered pair (or tuple) rather than unordered pair. 2 (1, 1) (2, 2) (2, 3) (1, 2) 1 (1, 3) 3 (2, 4) (3, 4) 4 (3, 3) (4, 4) Thus the set of edges E is just the represented relation on V. 28

Digraphs DEF: A directed graph (or digraph) G = (V, E ) consists of a non-empty set V of vertices (or nodes) and a set E of edges with E V V. The edge (a, b) is also denoted by a b and a is called the source of the edge while b is called the target of the edge. Q: For a set V with n elements, how many possible digraphs are there? 29

Digraphs A: The same as the number of relations on V, which is the number of subsets of V V so 2 n·n. 30

Directed Multigraphs If also want to allow multiple edges in a digraph, get a directed multigraph (or multi-digraph). 2 1 3 Q: How to use sets and functions to deal with multiple directed edges, loops? 31

Directed Multigraphs A: Have function with domain the edge set and codomain V V. 1 e 3 2 e 4 e 1 e 2 e 5 e 7 e 6 3 e 1 (1, 2), e 2 (1, 2), e 3 (2, 2), e 4 (2, 3), e 5 (2, 3), e 6 (3, 3), e 7 (3, 3) 32

Degree The degree of a vertex counts the number of edges that seem to be sticking out if you looked under a magnifying glass: 1 e 3 e 1 e 2 e 6 e 4 2 e 5 3 33

Degree The degree of a vertex counts the number of edges that seem to be sticking out if you looked under a magnifying glass: 1 e 3 e 1 e 2 e 6 e 4 2 e 5 magnify 3 34

Degree The degree of a vertex counts the number of edges that seem to be sticking out if you looked under a magnifying glass: 1 e 3 e 1 e 2 e 6 e 4 2 e 5 magnify 3 Thus deg(2) = 7 even though 2 only incident with 5 edges. Q: How to define this formally? 35

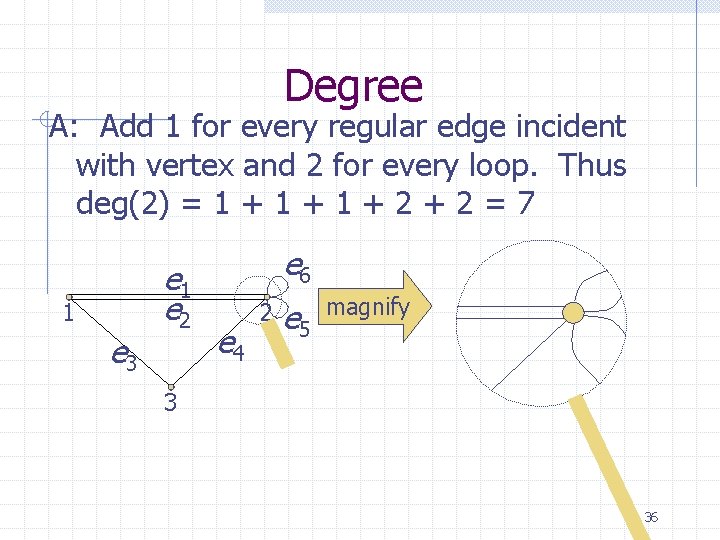
Degree A: Add 1 for every regular edge incident with vertex and 2 for every loop. Thus deg(2) = 1 + 1 + 2 = 7 1 e 3 e 1 e 2 e 6 e 4 2 e 5 magnify 3 36

Oriented Degree when Edges Directed The in-degree of a vertex (deg-) counts the number of edges that stick in to the vertex. The out-degree (deg+) counts the number sticking out. 2 1 3 Q: What are in-degrees and out-degrees of all the vertices? 37

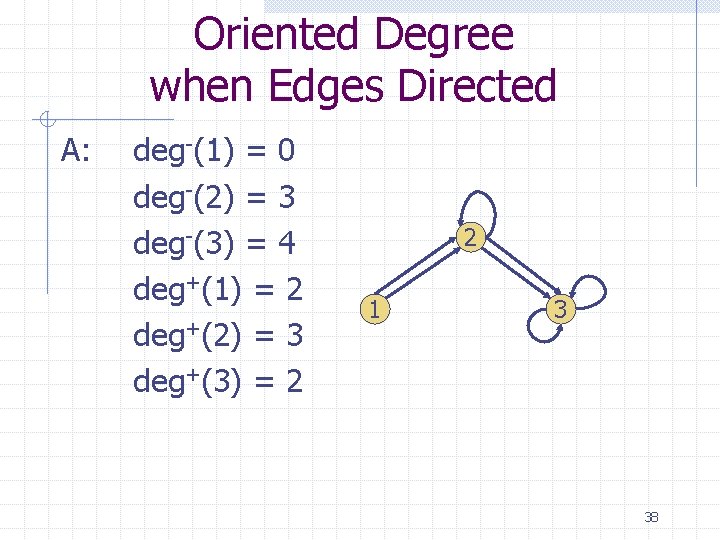
Oriented Degree when Edges Directed A: deg-(1) = 0 deg-(2) = 3 deg-(3) = 4 deg+(1) = 2 deg+(2) = 3 deg+(3) = 2 2 1 3 38

Graph Patterns Complete Graphs - Kn A simple graph is complete if every pair of distinct vertices share an edge. The notation Kn denotes the complete graph on n vertices. K 1 K 2 K 3 K 4 K 5 39

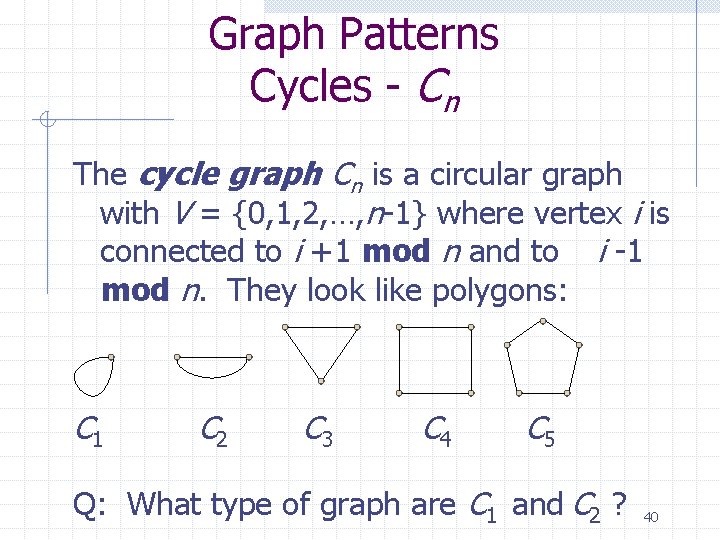
Graph Patterns Cycles - Cn The cycle graph Cn is a circular graph with V = {0, 1, 2, …, n-1} where vertex i is connected to i +1 mod n and to i -1 mod n. They look like polygons: C 1 C 2 C 3 C 4 C 5 Q: What type of graph are C 1 and C 2 ? 40

Graph Patterns Wheels - Wn A: Pseudographs The wheel graph Wn is just a cycle graph with an extra vertex in the middle: W 1 W 2 W 3 W 4 W 5 Usually consider wheels with 3 or more spokes only. 41

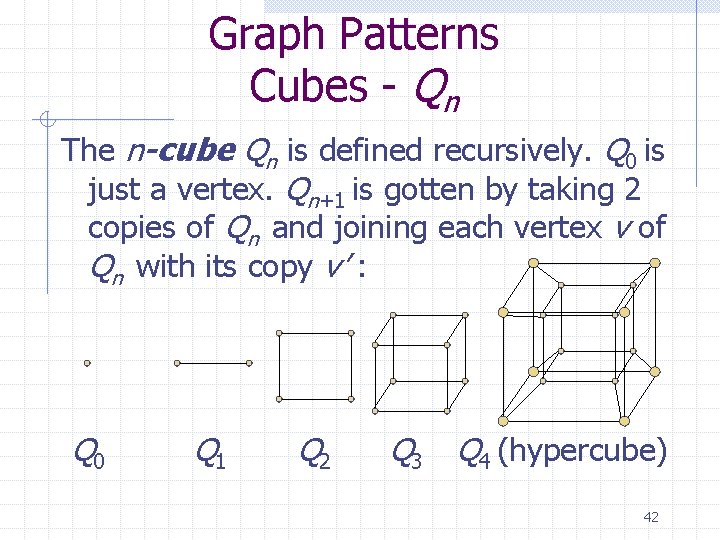
Graph Patterns Cubes - Qn The n-cube Qn is defined recursively. Q 0 is just a vertex. Qn+1 is gotten by taking 2 copies of Qn and joining each vertex v of Qn with its copy v’ : Q 0 Q 1 Q 2 Q 3 Q 4 (hypercube) 42

Subgraphs Notice that the 2 -cube occurs inside the 3 -cube . In other words, Q 2 is a subgraph of Q 3 : DEF: Let G = (V, E ) and H = (W, F ) be graphs. H is said to be a subgraph of G, if W V and F E. Q: How many Q 2 subgraphs does Q 3 have? 43

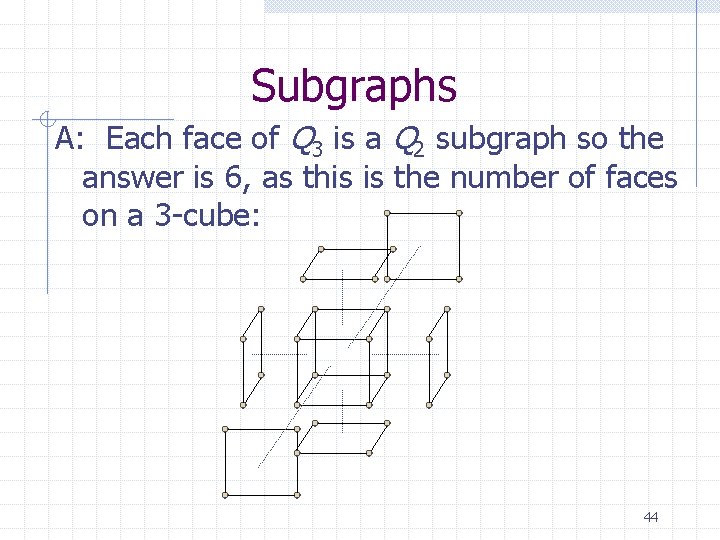
Subgraphs A: Each face of Q 3 is a Q 2 subgraph so the answer is 6, as this is the number of faces on a 3 -cube: 44

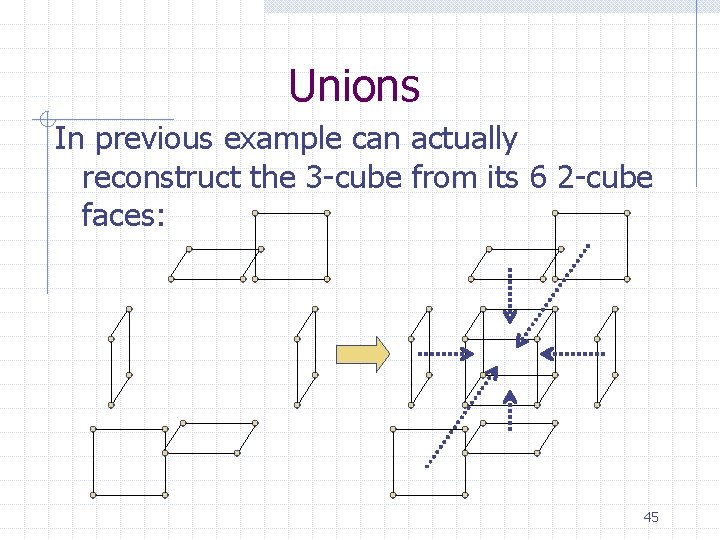
Unions In previous example can actually reconstruct the 3 -cube from its 6 2 -cube faces: 45

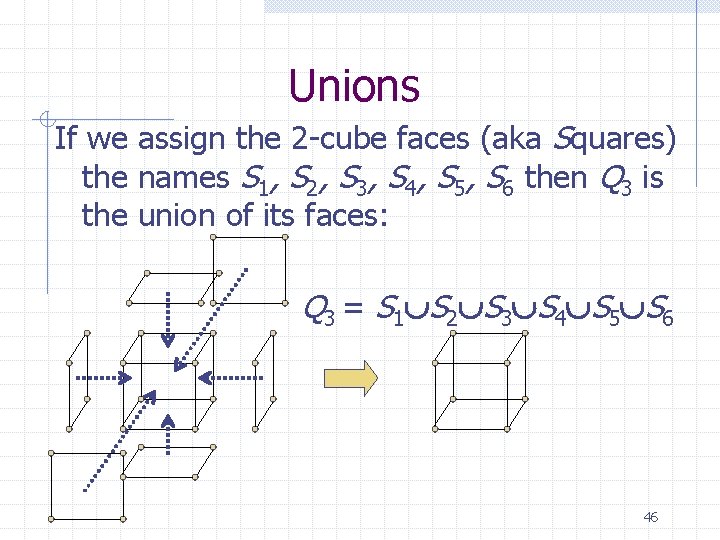
Unions If we assign the 2 -cube faces (aka Squares) the names S 1, S 2, S 3, S 4, S 5, S 6 then Q 3 is the union of its faces: Q 3 = S 1 S 2 S 3 S 4 S 5 S 6 46

Unions DEF: Let G 1 = (V 1, E 1 ) and G 2 = (V 2, E 2 ) be two simple graphs (and V 1, V 2 may or may not be disjoint). The union of G 1, G 2 is formed by taking the union of the vertices and edges. I. E: G 1 G 2 = (V 1 V 2, E 1 E 2 ). A similar definitions can be created for unions of digraphs, multigraphs, pseudographs, etc. 47

Thank you Share your ideas at any area; R. PURUSOTHAMAN, PGDCA, MCP, MCSE 1 MSC(CS) http: //thaman-j. tripod. com Thaman_j@yahoo. co. in Mob: 9843932212, 9791342123 48