Graphs shortest paths 15 211 Fundamental Data Structures

Graphs: shortest paths 15 -211 Fundamental Data Structures and Algorithms Ananda Guna April 3, 2003 1

Announcements § Start working on Homework #5. § Quiz #3 will be made available Friday 4/4 for 24 hours. 2

Recap 3

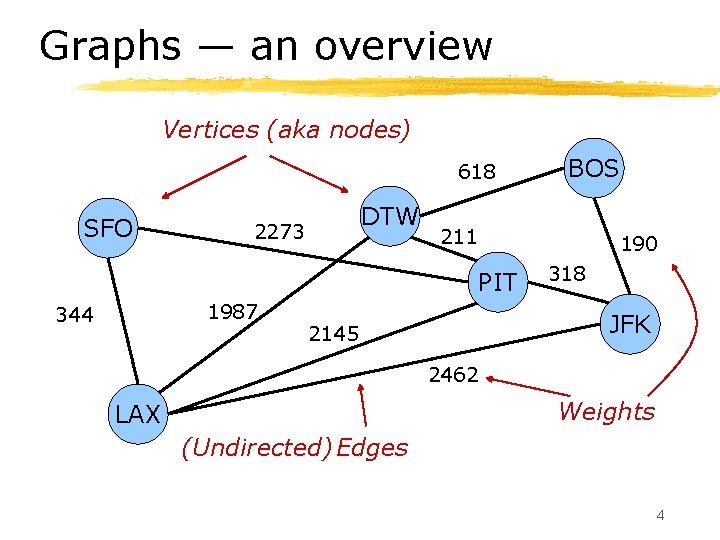
Graphs — an overview Vertices (aka nodes) 618 SFO DTW 2273 211 190 PIT 1987 344 BOS 318 JFK 2145 2462 Weights LAX (Undirected) Edges 4

Definitions § Graph G = (V, E) Ø Set V of vertices (nodes) Ø Set E of edges § Elements of E are pair (v, w) where v, w V. § An edge (v, v) is a self-loop. (Usually assume no self-loops. ) § Weighted graph Ø Elements of E are ((v, w), x) where x is a weight. § Directed graph (digraph) Ø The edge pairs are ordered § Undirected graph Ø The edge pairs are unordered § E is a symmetric relation § (v, w) E implies (w, v) E § In an undirected graph (v, w) and (w, v) are the same edge 5

Graph Questions § Is (x, y) an edge in the Graph? § Given x in V, does (x, x) in E? § Given x, y in V, what is the closest(cheapest) path from x to y (if any)? § What node v in V has the maximum(minimum) degree? § What is the largest connected sub-graph? § What is the complexity of algorithms for each of the above questions if Ø Graph is stored as an adjacency matrix? Ø Graph is stored as an adjacency list? 6

Graph Traversals § One of the fundamental operations in graphs. Find things such as Ø Count the total edges Ø Output the content in each vertex Ø Identify connected components § Before/during the tour - mark vertices Ø Visited Ø Not-visited Ø explored 7

Graph Traversals using. . § Queue - Store the vertices in a first-in, first out (FIFO) queue as follows. Put the starting node in a queue first. Dequeue the first element and add all its neighbors to the queue. Continue to explore the oldest unexplored vertices first. Thus the explorations radiate out slowly from the starting vertex. This describes a traversal technique known as breadth-first search. § Stack - Store vertices in a last-in, first-out (LIFO) stack. Explore vertices by going along a path, always visiting a new neighbor if one is available, and backing up only if all neighbors are discovered vertices. Thus our explorations quickly move away from start. This is called depth-first search. 8

Shortest Paths 9

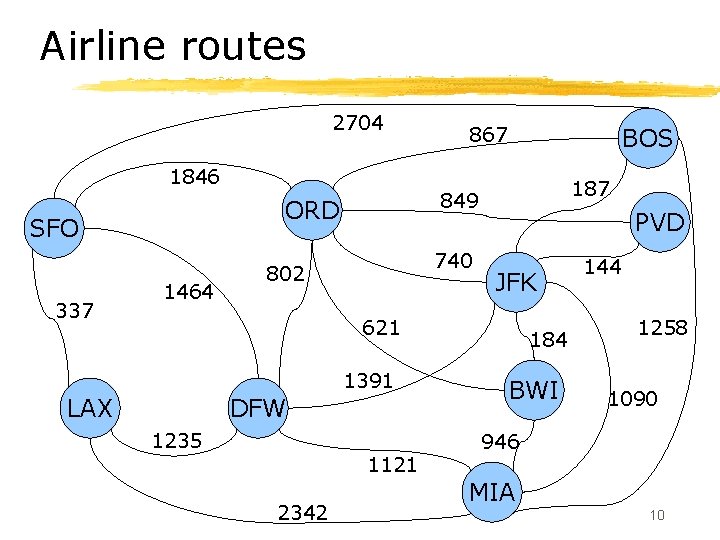
Airline routes 2704 1846 337 1464 BOS 187 849 ORD SFO 867 740 802 PVD JFK 621 1391 LAX DFW 1235 1121 2342 184 BWI 144 1258 1090 946 MIA 10

Single-source shortest path § Suppose we live in Baltimore (BWI) and want the shortest path to San Francisco (SFO). § One way to solve this is to solve the single-source shortest path problem: ØFind the shortest path from BWI to every city. 11

Single-source shortest path § While we may be interested only in BWI-to-SFO, there are no known algorithms that are asymptotically faster than solving the single-source problem for BWI-to-every-city. 12

Shortest paths § What do we mean by “shortest path”? § Minimize the number of layovers (i. e. , fewest hops). ØUnweighted shortest-path problem. § Minimize the total mileage (i. e. , fewest frequent-flyer miles ; -). ØWeighted shortest-path problem. 13

Many applications § Shortest paths model many useful real-world problems. ØMinimization of latency in the Internet. ØMinimization of cost in power delivery. ØJob and resource scheduling. ØRoute planning. 14

Unweighted Single-Source Shortest Path Algorithm 15

Unweighted shortest path § In order to find the unweighted shortest path, we will augment vertices and edges so that: Øvertices can be marked with an integer, giving the number of hops from the source node, and Øedges can be marked as either explored or unexplored. Initially, all edges are unexplored. 16

Unweighted shortest path § Algorithm: ØSet i to 0 and mark source node v with 0. ØPut source node v into a queue L 0. ØWhile Li is not empty: § Create new empty queue Li+1 § For each w in Li do: • For each unexplored edge (w, x) do: – mark (w, x) as explored – if x not marked, mark with i and enqueue x into Li+1 § Increment i. 17

Breadth-first search § This algorithm is a form of breadthfirst search. § Performance: O(|V|+|E|). § Q: Use this algorithm to find the shortest route (in terms of number of hops) from BWI to SFO. § Q: What kind of structure is formed by the edges marked as explored? 18

Use of a queue § It is very common to use a queue to keep track of: Ønodes to be visited next, or Ønodes that we have already visited. § Typically, use of a queue leads to a breadth-first visit order. § Breadth-first visit order is “cautious” in the sense that it examines every path of length i before going on to paths of length i+1. 19

Weighted Single-Source Shortest Path Algorithm (Dijkstra’s Algorithm) 20

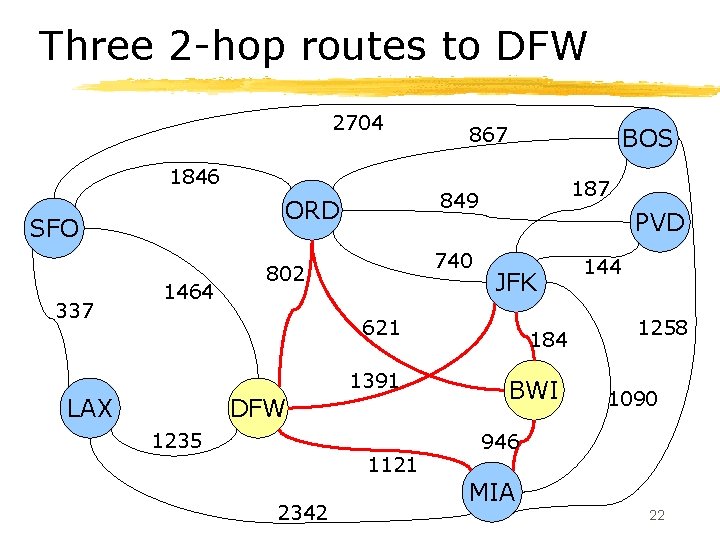
Weighted shortest path § Now suppose we want to minimize the total mileage. § Breadth-first search does not work! ØMinimum number of hops does not mean minimum distance. ØConsider, for example, BWI-to-DFW: 21

Three 2 -hop routes to DFW 2704 1846 337 1464 BOS 187 849 ORD SFO 867 740 802 PVD JFK 621 1391 LAX DFW 1235 1121 2342 184 BWI 144 1258 1090 946 MIA 22

A greedy algorithm § Assume that every city is infinitely far away. ØI. e. , every city is miles away from BWI (except BWI, which is 0 miles away). ØNow perform something similar to breadth-first search, and optimistically guess that we have found the best path to each city as we encounter it. ØIf we later discover we are wrong and find a better path to a particular city, then update the distance to that city. 23

Intuition behind Dijkstra’s alg. § For our airline-mileage problem, we can start by guessing that every city is miles away. ØMark each city with this guess. § Find all cities one hop away from BWI, and check whether the mileage is less than what is currently marked for that city. ØIf so, then revise the guess. § Continue for 2 hops, 3 hops, etc. 24

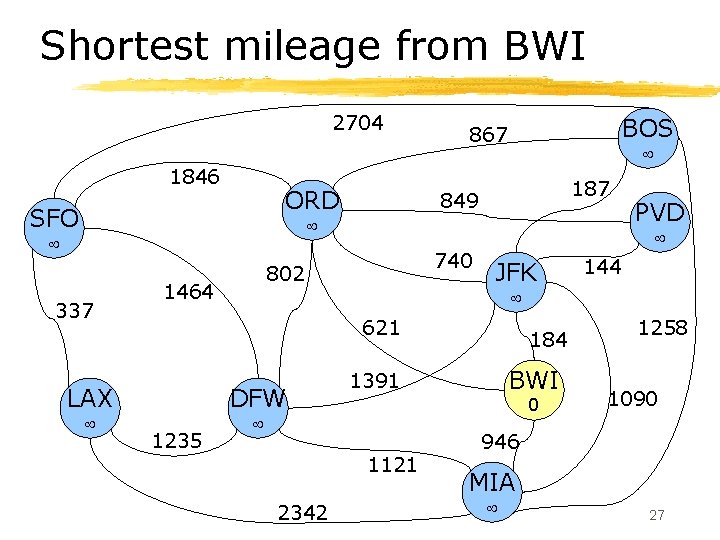
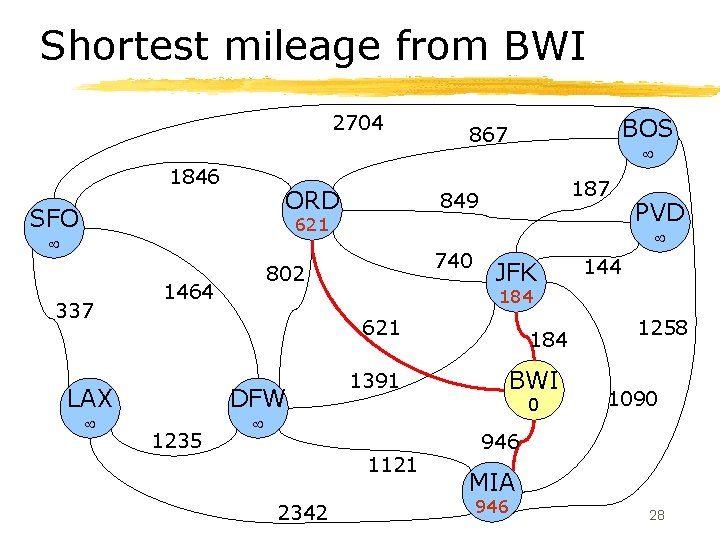
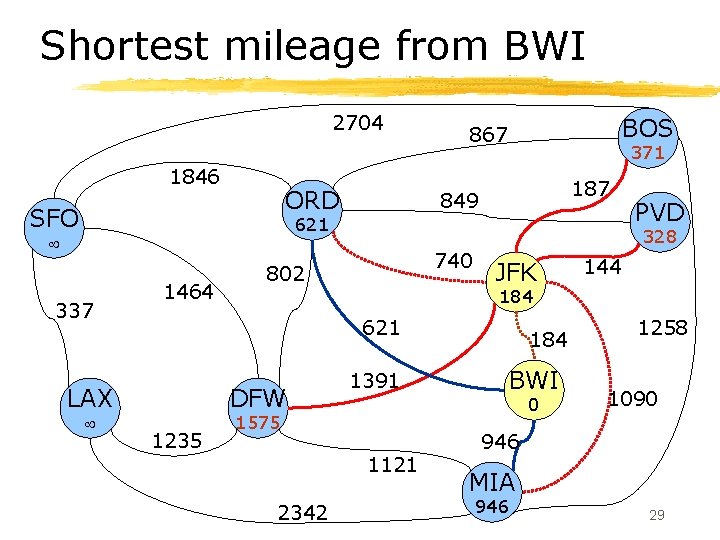
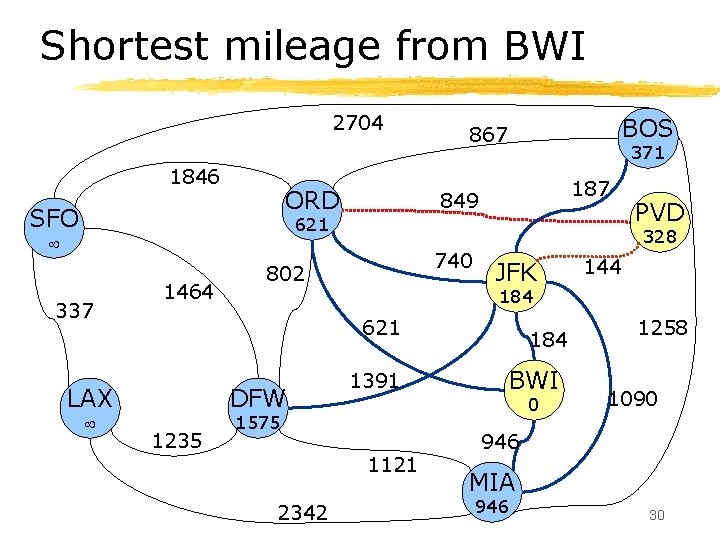
Dijkstra’s algorithm § Algorithm initialization: ØLabel each node with the distance , except start node, which is labeled with distance 0. § D[v] is the distance label for v. ØPut all nodes into a priority queue Q, using the distances as labels. 25

Dijkstra’s algorithm, cont’d § While Q is not empty do: Øu = Q. remove. Min Øfor each node z one hop away from u do: § if D[u] + miles(u, z) < D[z] then • D[z] = D[u] + miles(u, z) • change key of z in Q to D[z] § Note use of priority queue allows “finished” nodes to be found quickly (in O(log N) time). 26

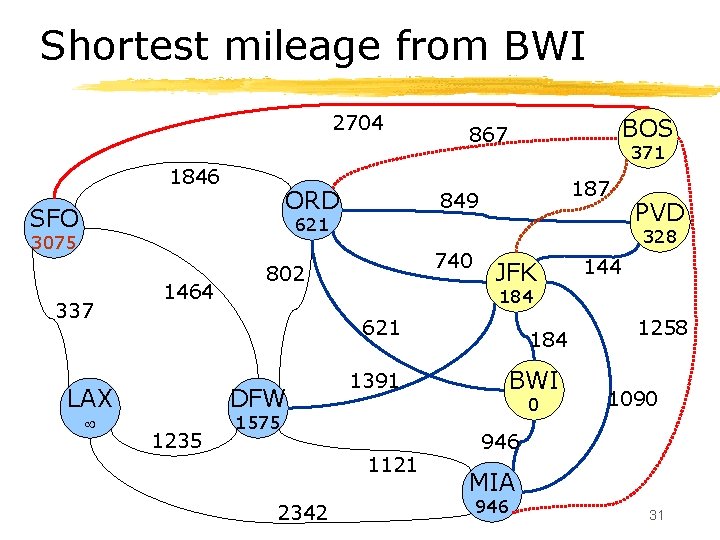
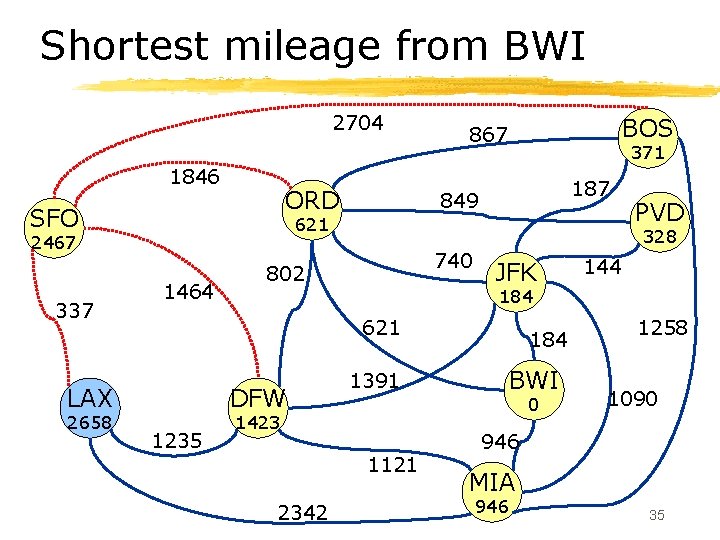
Shortest mileage from BWI 2704 1846 ORD SFO BOS 867 187 849 337 740 JFK DFW 1235 184 BWI 1391 0 1121 2342 144 621 LAX 802 1464 PVD 1258 1090 946 MIA 27

Shortest mileage from BWI 2704 1846 ORD SFO BOS 867 187 849 621 337 740 JFK DFW 1235 1391 184 BWI 0 1121 2342 144 184 621 LAX 802 1464 PVD 1258 1090 946 MIA 946 28

Shortest mileage from BWI 2704 1846 ORD SFO BOS 867 371 187 849 621 337 1464 328 740 802 JFK DFW 1235 1391 184 BWI 0 1575 1121 2342 144 184 621 LAX PVD 1258 1090 946 MIA 946 29

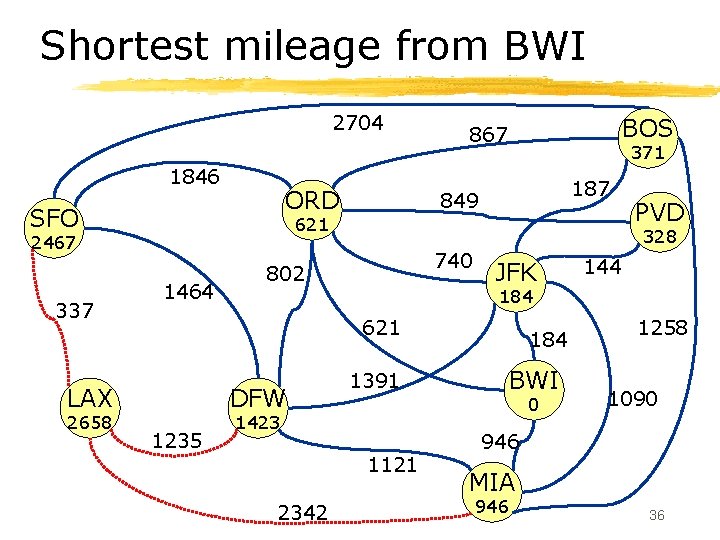
Shortest mileage from BWI 2704 1846 ORD SFO BOS 867 371 187 849 621 337 1464 328 740 802 JFK DFW 1235 1391 184 BWI 0 1575 1121 2342 144 184 621 LAX PVD 1258 1090 946 MIA 946 30

Shortest mileage from BWI 2704 1846 ORD SFO BOS 867 371 187 849 621 3075 337 1464 328 740 802 JFK DFW 1235 1391 184 BWI 0 1575 1121 2342 144 184 621 LAX PVD 1258 1090 946 MIA 946 31

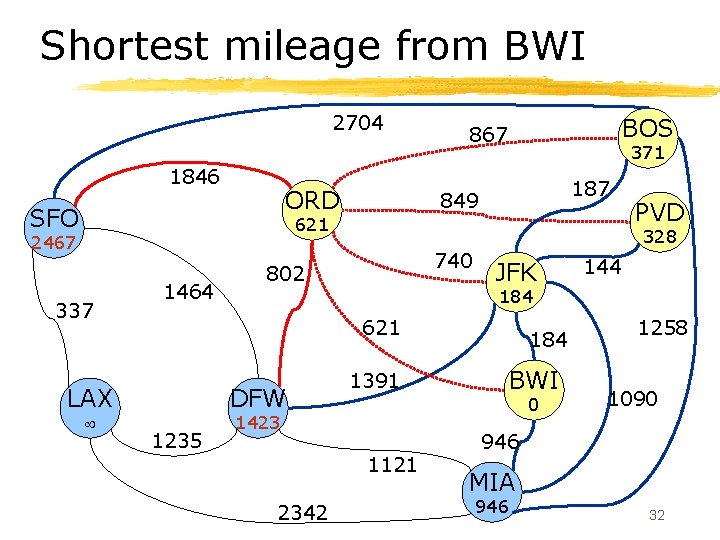
Shortest mileage from BWI 2704 1846 ORD SFO BOS 867 371 187 849 621 2467 337 1464 328 740 802 JFK DFW 1235 1391 184 BWI 0 1423 1121 2342 144 184 621 LAX PVD 1258 1090 946 MIA 946 32

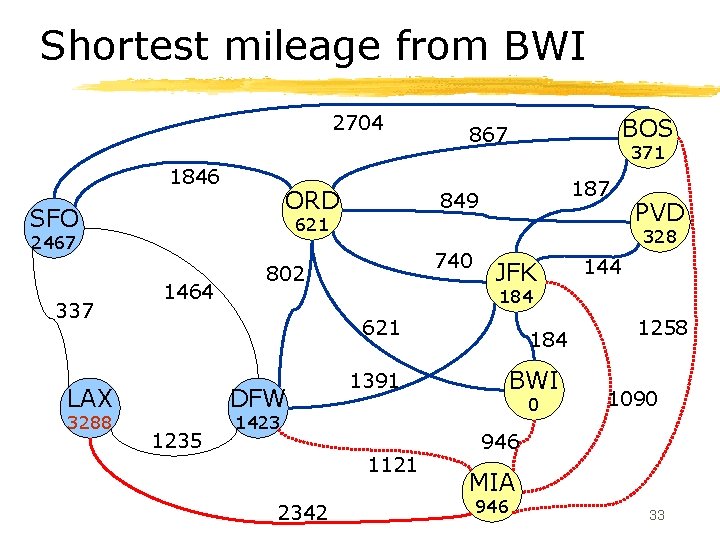
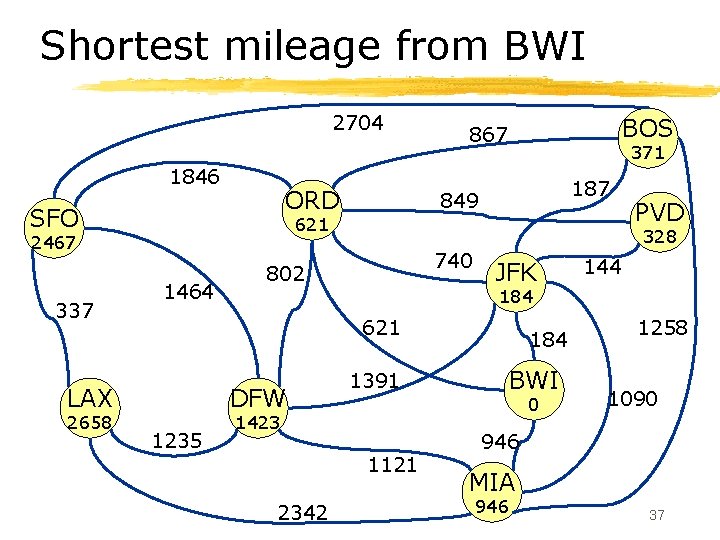
Shortest mileage from BWI 2704 1846 ORD SFO 1464 187 849 740 802 DFW 1235 JFK 144 184 1391 184 BWI 0 1423 1121 2342 PVD 328 621 LAX 3288 371 621 2467 337 BOS 867 1258 1090 946 MIA 946 33

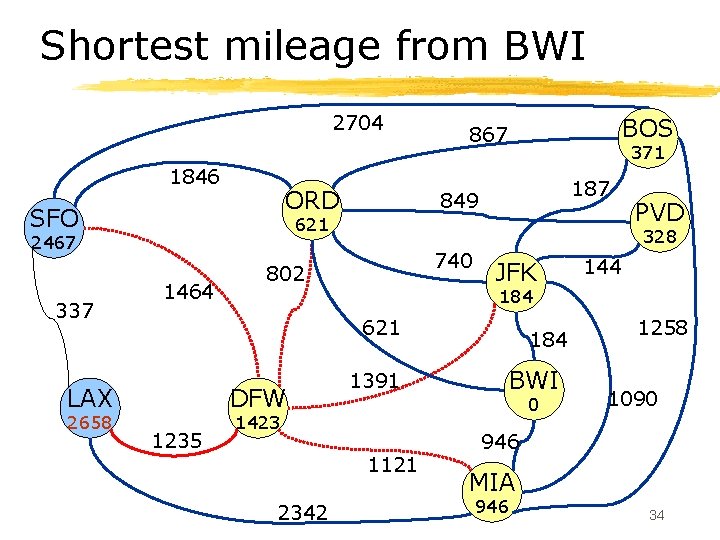
Shortest mileage from BWI 2704 1846 ORD SFO 1464 187 849 740 802 DFW 1235 JFK 144 184 1391 184 BWI 0 1423 1121 2342 PVD 328 621 LAX 2658 371 621 2467 337 BOS 867 1258 1090 946 MIA 946 34

Shortest mileage from BWI 2704 1846 ORD SFO 1464 187 849 740 802 DFW 1235 JFK 144 184 1391 184 BWI 0 1423 1121 2342 PVD 328 621 LAX 2658 371 621 2467 337 BOS 867 1258 1090 946 MIA 946 35

Shortest mileage from BWI 2704 1846 ORD SFO 1464 187 849 740 802 DFW 1235 JFK 144 184 1391 184 BWI 0 1423 1121 2342 PVD 328 621 LAX 2658 371 621 2467 337 BOS 867 1258 1090 946 MIA 946 36

Shortest mileage from BWI 2704 1846 ORD SFO 1464 187 849 740 802 DFW 1235 JFK 144 184 1391 184 BWI 0 1423 1121 2342 PVD 328 621 LAX 2658 371 621 2467 337 BOS 867 1258 1090 946 MIA 946 37

Dijkstra’s algorithm, recap § While Q is not empty do: Øu = Q. remove. Min Øfor each node z one hop away from u do: § if D[u] + miles(u, z) < D[z] then • D[z] = D[u] + miles(u, z) • change key of z in Q to D[z] 38

Quiz break § Would it be better to use an adjacency list or an adjacency matrix for Dijkstra’s algorithm? § What is the running time of Dijkstra’s algorithm, in terms of |V| and |E|? 39

Complexity of Dijkstra § Adjacency matrix version Dijkstra finds shortest path from one vertex to all others in O(|V|2) time § If |E| is small compared to |V|2, use a priority queue to organize the vertices in V -S, where V is the set of all vertices and S is the set that has already been explored § So total of |E| updates each at a cost of O(log |V|) § So total time is O(|E| log|V|) 40

The All Pairs Shortest Path Algorithm (Floyd’s Algorithm) 41

Finding all pairs shortest paths § Assume G=(V, E) is a graph such that c[v, w] 0, where C is the matrix of edge costs. § Find for each pair (v, w), the shortest path from v to w. That is, find the matrix of shortest paths § Certainly this is generalization of Dijkstra’s. § Note: For later discussions assume |V| = n and |E| = m 42

Floyd’s Algorithm § A[i][j] = C(i, j) if there is an edge (i, j) § A[i][j] = infinity(inf) if there is no edge (i, j) Graph “adjacency” matrix A is the shortest path matrix that uses 1 or fewer edges 43

Floyd ctd. . § To find shortest paths that uses 2 or fewer edges find A 2, where multiplication defined as min of sums instead sum of products § That is (A 2)ij = min{ Aik + Akj | k =1. . n} § This operation is O(n 3) § Using A 2 you can find A 4 and then A 8 and so on § Therefore to find An we need log n operations § Therefore this algorithm is O(log n* n 3) § We will consider another algorithm next 44

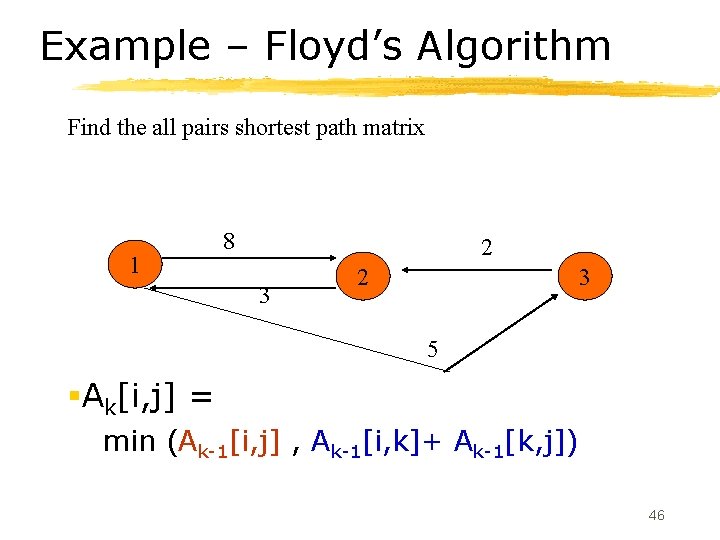
Floyd-Warshall Algorithm § This algorithm uses nxn matrix A to compute the lengths of the shortest paths using a dynamic programming technique. § Let A[i, j] = c[i, j] for all i, j & i j § If (i, j) is not an edge, set A[i, j]=infinity and A[i, i]=0 § Ak[i, j] = min (Ak-1[i, j] , Ak-1[i, k]+ Ak-1[k, j]) 45

Example – Floyd’s Algorithm Find the all pairs shortest path matrix 1 8 2 3 5 §Ak[i, j] = min (Ak-1[i, j] , Ak-1[i, k]+ Ak-1[k, j]) 46

Floyd-Warshall Implementation § initialize A[i, j] = C[i, j] § initialize all A[i, i] = 0 § for k from 1 to n for i from 1 to n for j from 1 to n if (A[i, j] > A[i, k]+A[k, j]) A[i, j] = A[i, k]+A[k, j]; § The complexity of this algorithm is O(n 3) 47

Negative Weighted Single-Source Shortest Path Algorithm (Bellman-Ford Algorithm) 48

Bellman-Ford Algorithm Definition: An efficient algorithm to find the shortest paths from a single source vertex to all other vertices in a weighted, directed graph. Weights may be negative. The algorithm initializes the distance to the source vertex to 0 and all other vertices to. It then does V-1 passes (V is the number of vertices) over all edges relaxing, or updating, the distance to the destination of each edge. Finally it checks each edge again to detect negative weight cycles, in which case it returns false. The time complexity is O(VE), where E is the number of edges. Source: NIST 49

Bellman-Ford Shortest Paths § We want to compute the shortest path from the start to every node in the graph. As usual with DP, let's first just worry about finding the LENGTH of the shortest path. We can later worry about actually outputting the path. § To apply the DP approach, we need to break the problem down into sub-problems. We will do that by imagining that we want the shortest path out of all those that use i or fewer edges. We'll start with i=0, then use this to compute for i=1, 2, 3, . . 50

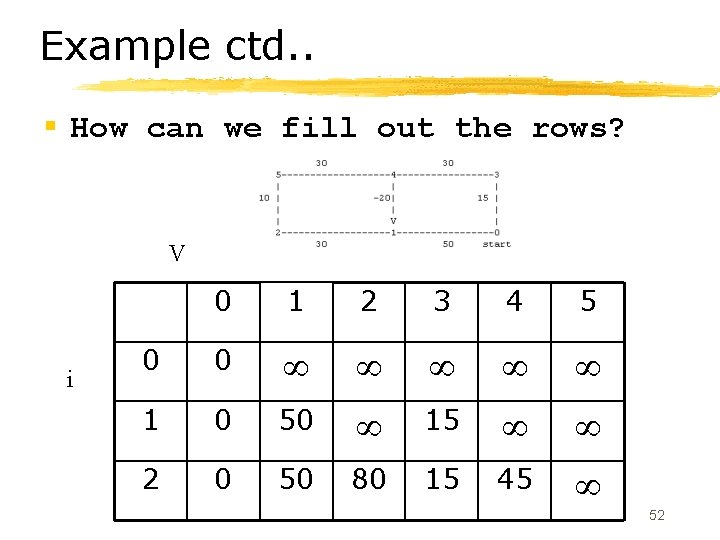
Example § For each edge (u, v), let's denote its length by C(u, v)) § Let d[i][v] = distance from start to v using the shortest path out of all those that use i or fewer edges, or infinity if you can't get there with <= i edges. 51

Example ctd. . § How can we fill out the rows? V i 0 1 2 3 4 5 0 0 1 0 50 15 2 0 50 80 15 45 52

Example ctd. . § Can we get ith row from i-1 th row? § for v != start, d[v][i] = MIN d[x][i-1] + len(x, v) x->v § We know minimum path to come to x using < i nodes. So for all x that can reach v, find the minimum such sum (in blue) among all x § Assume d[start][i] = 0 for all i 53

Completing the table d[v][i] = MIN d[x][i-1] + len(x, v) x->v 1 2 3 4 5 0 0 0 1 0 50 15 2 0 50 80 15 45 3 0 4 0 54

Questions § Question: How large does i ever have to be? (Remember, there are no negative-weight cycles) § Question: what is the total running time in terms of |V| and |E|? 55

Next Week § Work on Homework #5 § We will talk more about graph traversals and topological sorting § We will discuss Minimum Spanning Trees (Prim’s Algorithm) § Read Chapter 14 56