Graphs Ryerson Dont be dense try hypergraphs Anthony

Graphs @ Ryerson Don’t be dense, try hypergraphs! Anthony Bonato Ryerson University 1

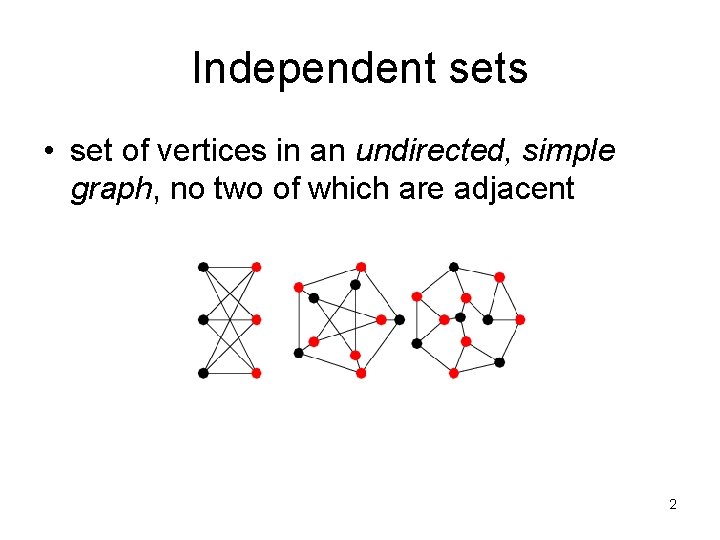
Independent sets • set of vertices in an undirected, simple graph, no two of which are adjacent 2

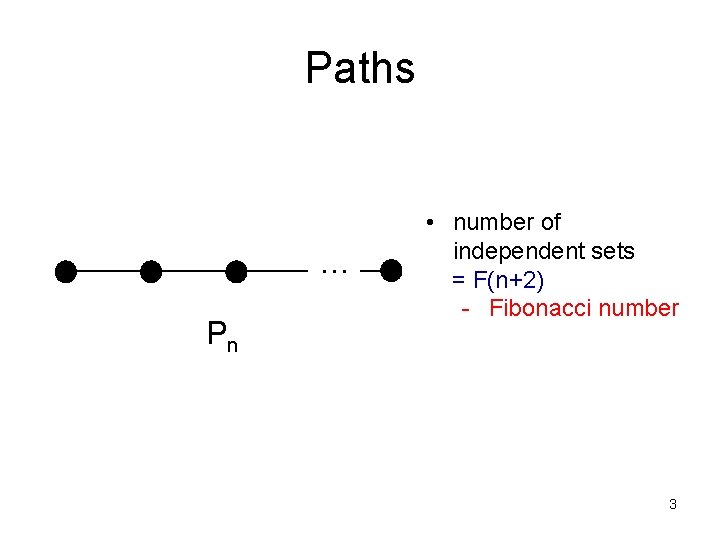
Paths … Pn • number of independent sets = F(n+2) - Fibonacci number 3

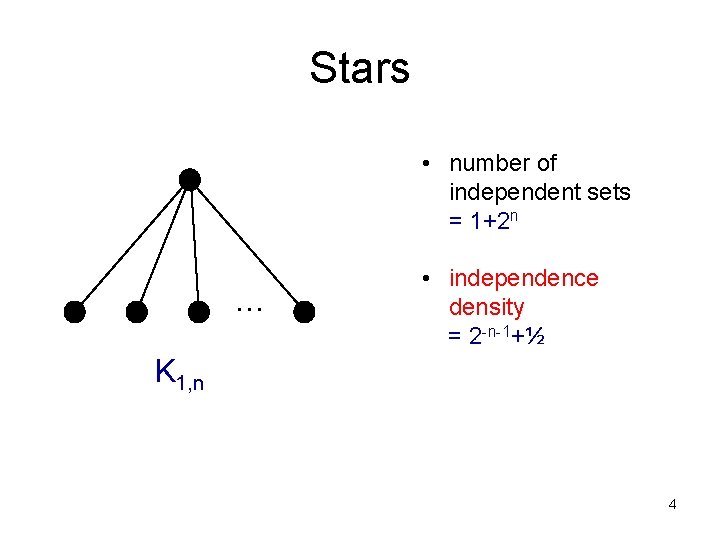
Stars • number of independent sets = 1+2 n … • independence density = 2 -n-1+½ K 1, n 4

Independence density • G a graph of order n • i(G) = number of independent sets in G (including ∅) – Fibonacci number of G • id(G) = i(G) / 2 n – independence density of G – rational in (0, 1] 5

Properties • if G is a spanning subgraph of H, then i(H) ≤ i(G) – (possibly) fewer edges in G • i(G U H) = i(G)i(H) 6

Monotonicity • if G is subgraph of H, then id(H) ≤ id(G) – G has an edge, then: id(G) ≤ id(K 2) = ¾ Proof: Say G has order m and H has order n. id(H) = i(H) / 2 n ≤ i(G U (H-G)) / 2 n (disjoint union) = i(G)i(H-G) / 2 m 2 n-m = id(G)id(H-G) ≤ id(G). • id(G U H) = id(G)id(H) 7

Infinite graphs? • 8

Chains • 9

Existence and uniqueness • 10

Examples • infinite star: id(K 1, ∞) = 1/2 • one-way infinite path: id(P∞) = 0 11

Bounds on id • 12

Rationality Theorem (BBKP, 11) Let G be a countable graph. 1. id(G) is rational. 2. The closure of the set {id(G): G countable} is a subset of the rationals. 13

Aside: other densities • many other density notions for graphs and hypergraphs: – upper density – homomorphism density – Turán density – co-degree density – cop density, … 14

Question • hereditary graph class X: closed under induced subgraphs • egs: X = independent sets; cliques; triangle-free graphs; perfect graphs; H-free graphs • Xd(G) = proportion of subsets which induce a graph in X – generalizes to infinite graphs via chains • is Xd(G) rational? 15

Try hypergraphs! • hypergraph H = (V, E), E = hyperedges • independent set: does not contain a hyperedge • id(H) defined analogously – extend to infinite hypergraphs by continuity – well-defined 16

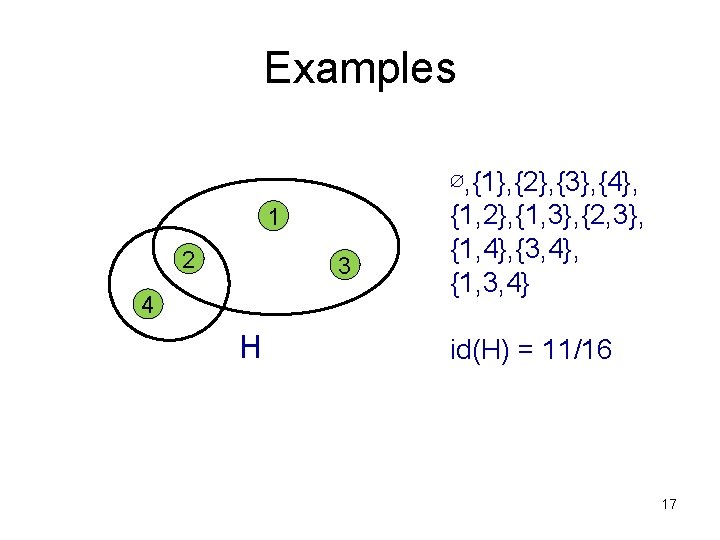
Examples 1 2 3 4 H ∅, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {2, 3}, {1, 4}, {3, 4}, {1, 3, 4} id(H) = 11/16 17

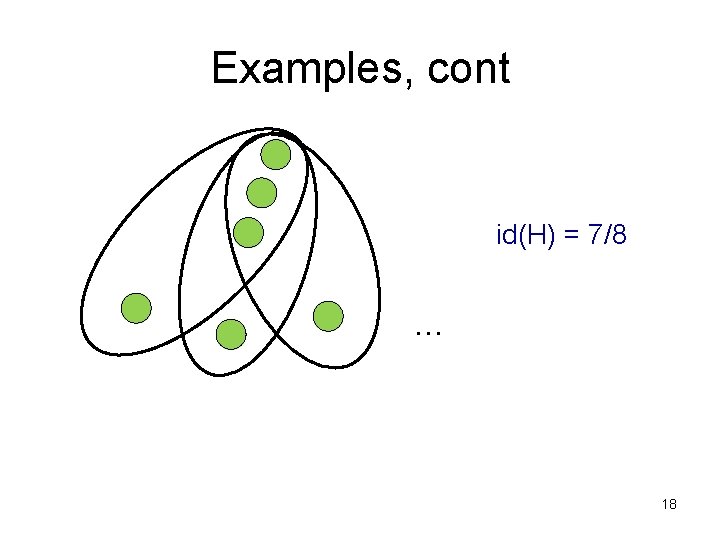
Examples, cont id(H) = 7/8 … 18

Hypergraph id’s examples: 1. graph, E = subsets of vertices containing a copy of K 2 – recovers the independence density of graphs 2. graph, fix a finite graph F; E = subsets of vertices containing a copy of F – F-free density (generalizes (1)). 3. relational structure (graphs, digraphs, orders, etc); F a set of finite structures; E = subsets of vertices containing a member of F – F-free density of a structure (generalizes (2)) 19

Bounds on id • 20

Rationality • rank k hypergraph: hyperedges bounded in cardinality by k > 0 – finite rank: rank k for some k Theorem (BBMP, 14): If H has finite rank, then id(H) is rational. 21

Sketch of proof • notation: for finite disjoint sets of vertices A and B id. A, B(H) = density of independent sets containing A and not B • analogous properties to id(H) = id∅, ∅(H) 22

Properties of id. A, B(H) • 23

Out-sets • for a given A, B, and any hyperedge S such that S∩B = ∅, the set S A is the out-set of S relative to A and B – example: A B S • notation: idr. A, B(H) denotes that every out-set has cardinality at most r • note that: idk∅, ∅(H) = id(H) 24

Claims • 25

Final steps… • 26

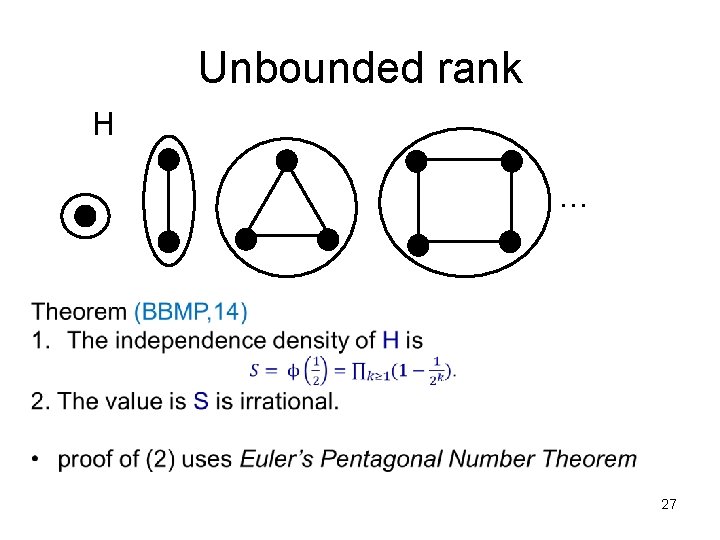
Unbounded rank H … 27

Any real number • case of finite, but unbounded hyperedges • Hunb = {x: there is a countable hypergraph H with id(H) = x} Theorem (BBMP, 14) Hunb = [0, 1]. • contrasts with rank k case, where there exist gaps such as (1 -1/2 k, 1) 28

Independence polynomials • 29

Independence densities at x • 30

Examples, continued • 31

Asymptotic behaviour • 32

Sketch of proof • 33

Examples, continued • 34

Future directions • classify gaps among densities for given hypergraphs – eg: rank k, (1 -1/2 k, 1) is a gap • rationality of closure of set of id’s for rank k hypergraphs • which hypergraphs have jumping points, and what are their values? 35

General densities • 36