Graphs Ryerson Conjectures on Cops and Robbers 2

Graphs @ Ryerson Conjectures on Cops and Robbers 2. 0 Anthony Bonato Ryerson University Toronto, Canada 1

G@R 100 • The sum of the first nine primes is 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 = 100 • 100 is the sum of the first four cube numbers: 1 + 8 + 27 + 64 = 100 • There are 4950 edges in K 100 • The crossing number of K 11 is 100 • The cop number of Q 199 is 100 Cops and Robbers 2

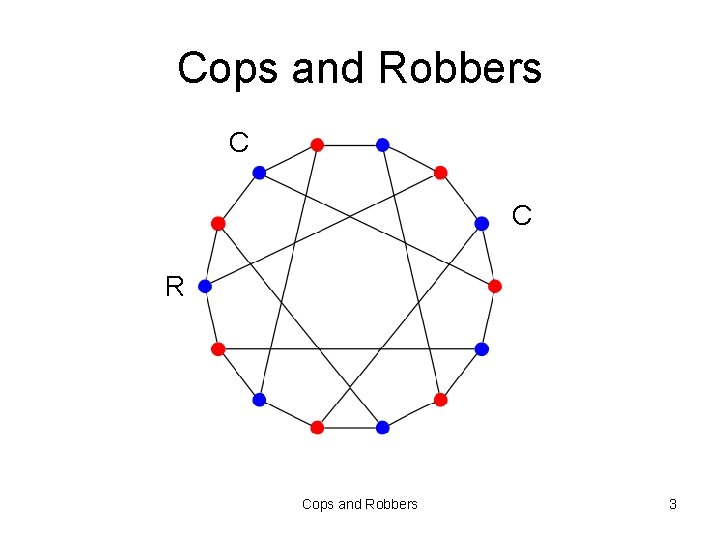
Cops and Robbers C C R Cops and Robbers 3

Cops and Robbers • played on an undirected graph G • two players Cops C and robber R play at alternate time-steps (cops first) with perfect information • players move to vertices along edges; may move to neighbors or pass • cops try to capture (i. e. land on) the robber, while robber tries to evade capture • minimum number of cops needed to capture the robber is the cop number c(G) – well-defined as c(G) ≤ |V(G)| Cops and Robbers 4

Observations • Cops and Robbers 5

Applications of Cops and Robbers • robotics – mobile computing – missile-defense – gaming • counter-terrorism – intercepting messages or agents Cops and Robbers 6

Conjectures • conjectures and problems on Cops and Robbers coming from five different directions, touch on various aspects of graph theory: – structural, algorithmic, probabilistic, topological… Cops and Robbers 7

1. How big can the cop number be? • c(n) = maximum cop number of a connected graph of order n Meyniel Conjecture: c(n) = O(n 1/2). Cops and Robbers 8

Cops and Robbers 9

Henri Meyniel, courtesy Geňa Hahn Cops and Robbers 10

Sketch of Frankl’s proof • Cops and Robbers 11

State-of-the-art • (Lu, Peng, 13) proved that – independently proved by (Frieze, Krivelevich, Loh, 11) and (Scott, Sudakov, 11) Cops and Robbers 12

For random graphs • (Bollobás, Kun, Leader, 13): if p = p(n) ≥ 2. 1 log n/ n, then a. a. s. c(G(n, p)) ≤ 160000 n 1/2 log n • (Prałat, Wormald, 16): proved Meyniel’s conjecture a. a. s. for all p = p(n) • (Prałat, Wormald, 16+): holds a. a. s. for random d-regular graphs, for d ≥ 3 Cops and Robbers 13

Graph classes • (Andreae, 86): H-minor free graphs have cop number bounded by a constant. • (Joret et al, 10): H-free class graphs have bounded cop number iff each component of H is a tree with at most 3 leaves. • (Lu, Peng, 13): Meyniel’s conjecture holds for diameter 2 graphs, bipartite diameter 3 graphs. Cops and Robbers 14

Questions Soft Meyniel’s conjecture: for some ε > 0, c(n) = O(n 1 -ε). • Meyniel’s conjecture in other graphs classes? – bipartite graphs – diameter 3 – claw-free Cops and Robbers 15

How close to n 1/2? • consider a finite projective plane P – two lines meet in a unique point – two points determine a unique line – exist 4 points, no line contains more than two of them • q 2+q+1 points; each line (point) contains (is incident with) q+1 points (lines) • incidence graph (IG) of P: – bipartite graph G(P) with red nodes the points of P and blue nodes the lines of P – a point is joined to a line if it is on that line Cops and Robbers 16

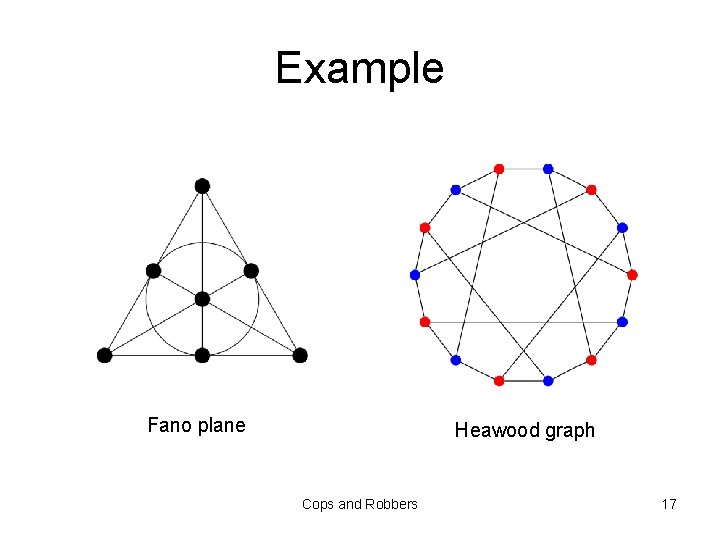
Example Fano plane Heawood graph Cops and Robbers 17

Meyniel extremal families • a family of connected graphs (Gn: n ≥ 1) is Meyniel extremal if there is a constant d > 0, such that for all n ≥ 1, c(Gn) ≥ dn 1/2 • IG of projective planes: girth 6, (q+1)-regular, so have cop number ≥ q+1 – order 2(q 2+q+1) – Meyniel extremal (must fill in non-prime orders) • other examples of Meyniel extremal families come from combinatorial designs and finite geometries (B, Burgess, 2013) Cops and Robbers 18

(BB, 13) New ME families Cops and Robbers 19

Polarity graphs • suppose PG(2, q) has points P and lines L. A polarity is a function π: P→ L such that for all points p, q, p ϵ π(q) iff q ϵ π(p). • eg of orthogonal polarity: point mapped to its orthogonal complement • polarity graph: vertices are points, x and y adjacent if xϵ π(y) Cops and Robbers 20

Properties of polarity graphs • • order q 2+q+1 (q, q+1)-regular C 4 -free diameter 2 Cops and Robbers 21

Meyniel Extremal • Theorem (Bonato, Burgess, 13) Let q be a prime power. If Gq is a polarity graph of PG(2, q), then q/2 ≤ c(Gq) ≤ q + 1. Cops and Robbers 22

Lower bounds Theorem (Bonato, Burgess, 13) If G is connected and K 2, t-free, then c(G) ≥ δ(G) / t. – applies to polarity graphs: t = 2 Cops and Robbers 23

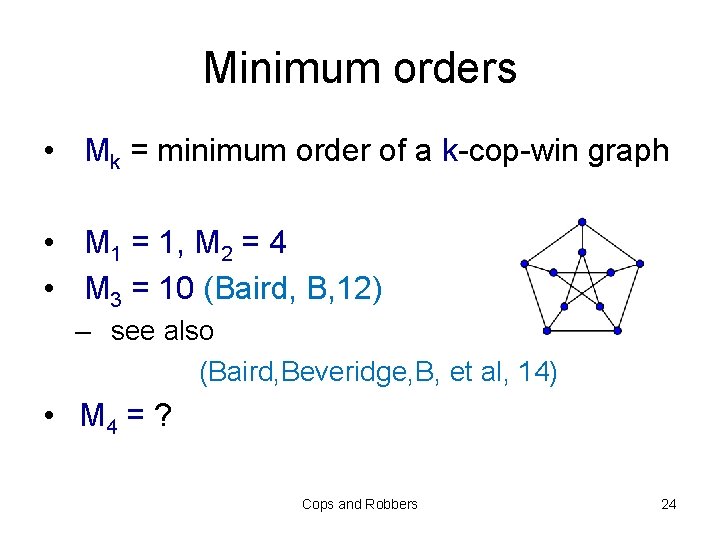
Minimum orders • Mk = minimum order of a k-cop-win graph • M 1 = 1, M 2 = 4 • M 3 = 10 (Baird, B, 12) – see also (Baird, Beveridge, B, et al, 14) • M 4 = ? Cops and Robbers 24

2. Complexity • (Berrarducci, Intrigila, 93), (Hahn, Mac. Gillivray, 06), (B, Chiniforooshan, 09): “c(G) ≤ s? ” s fixed: in P; running time O(n 2 s+3), n = |V(G)| • (Fomin, Golovach, Kratochvíl, Nisse, Suchan, 08): if s not fixed, then computing the cop number is NPhard Cops and Robbers 25

Questions Goldstein, Reingold Conjecture: if s is not fixed, then computing the cop number is EXPTIMEcomplete. – same complexity as say, generalized chess • settled by (Kinnersley, 15) JCTB Conjecture: if s is not fixed, then computing the cop number is not in NP. Cops and Robbers 26

3. Genus • (Aigner, Fromme, 84) planar graphs (genus 0) have cop number ≤ 3. • (Clarke, 02) outerplanar graphs have cop number ≤ 2. Cops and Robbers 27

Questions • characterize planar (outer-planar) graphs with cop number 1, 2, and 3 (1 and 2) • is the dodecahedron the unique smallest order planar 3 -cop-win graph? Cops and Robbers 28

Higher genus Schroeder’s Conjecture: If G has genus k, then c(G) ≤ k +3. • true for k = 0 • (Schroeder, 01): true for k = 1 (toroidal graphs) • (Quilliot, 85): c(G) ≤ 2 k +3. • (Schroeder, 01): c(G) ≤ floor(3 k/2) +3. Cops and Robbers 29

5. Variants Good guys vs bad guys games in graphs good bad slow medium fast helicopter eternal security traps, tandem-win, Lazy Cops and Robbers medium robot vacuum Cops and Robbers edge searching, Cops and Fast Robber fast cleaning distance k Cops and Robbers The Angel on disjoint edge and Devil sets seepage Helicopter Cops and Robbers, Marshals, The Angel and Devil, Firefighter helicopter Hex 30

Distance k Cops and Robber (B, Chiniforooshan, 09) • cops can “shoot” robber at some specified distance k • play as in classical game, but capture includes case when robber is distance k from the cops – k = 0 is the classical game C k=1 R Cops and Robbers 31

Distance k cop number: ck(G) • ck(G) = minimum number of cops needed to capture robber at distance at most k • G connected implies ck(G) ≤ diam(G) – 1 • for all k ≥ 1, ck(G) ≤ ck-1(G) Cops and Robbers 32

When does one cop suffice? • (RJN, Winkler, 83), (Quilliot, 78) cop-win graphs ↔ cop-win orderings • provide a structural/ordering characterization of cop-win graphs for: – – directed graphs distance k Cops and Robbers invisible robber; cops can use traps or alarms/photo radar (Clarke et al, 00, 01, 06…) infinite graphs (Bonato, Hahn, Tardif, 10) Cops and Robbers 33

Lazy Cops and Robbers • Cops and Robbers 34

Questions on lazy cops • Cops and Robbers 35

Cops and Robbers 36

Cops and Robbers 37

Zombie horde Cops and Robbers 38

Zombies and Survivors • set of zombies, one survivor • players move at alternate ticks of the clock, from vertex to vertex along edges • zombies choose their initial locations u. a. r. • at each step the zombies move along a shortest path connected to the survivor – if more than one such path, then they choose one u. a. r. • zombies win if one or more can eat the survivor – land on the survivor’s vertex • otherwise, survivor wins • NB: zombies have no strategy! Cops and Robbers 39

(B, Mitsche, Perez-Gimenez, Pralat, 16) • sk(G): probability survivor wins if k zombies play, assuming optimal play • sk+1 (G) ≤ sk (G) for all k, and sk(G) → 0 as k → ∞ • zombie number of G is z(G) = min{k ≥ c(G): sk(G) ≤ ½} – well-defined • z(G) represents the minimum number of zombies such that the probability that they eat the survivor is > ½ – note that c(G) ≤ z(G) • Z(G) = z(G) / c(G): cost of being undead Cops and Robbers 40

Deterministic Zombies • deterministic version of the game: (Fitzpatrick, Howell, Messinger, Pike, 16+) at the SIAM DM 2014 conference in Minneapolis • in the deterministic version, the zombies choose their location, and can choose their geodesics if more than one • example: where c(G) = 2 < z(G) = 3 Cops and Robbers 41

Cartesian grids • (Tosic, 87) c(G H) ≤ c(G) + c(H) Theorem (BMPGP, 16) For n ≥ 2, z(Pn Pn) = 2, so Z(Pn Pn) =1. Cops and Robbers 42

Toroidal grids • Cops and Robbers 43

• survivor fights back? • (Finbow, Gordinowicz, Haidar, Kinnersley, Mitsche, Pralat, Stacho, 13): The robber strikes back In: Proceedings of ICC 3, 2013. Cops and Robbers 44

Cops and Robbers 45

1. . A. Bonato, R. J. Nowakowski, Sketchy Tweets: Ten Minute Conjectures in Graph Theory, The Mathematical Intelligencer 34 (2012) 8 -15. Cops and Robbers 46