Graphs Rosen 8 1 8 2 There Are

Graphs Rosen 8. 1, 8. 2

There Are Many Uses for Graphs! • • Networks Data organizations Scene graphs Geometric simplification Program structure and processes Lots of others…. Also applications (e. g. , species structure— phylogeny tree)

Definitions • A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. • A multigraph G = (V, E) consists of a set V of vertices, a set E of edges, and a function f from E to {{u, v} | u, v V, u ≠ v}. The edges e 1 and e 2 are called multiple or parallel edges if f(e 1) = f(e 2).

Properties Simple graph – Undirected – Single edges – No loops Multigraph – Undirected – Multiple edges – No loops

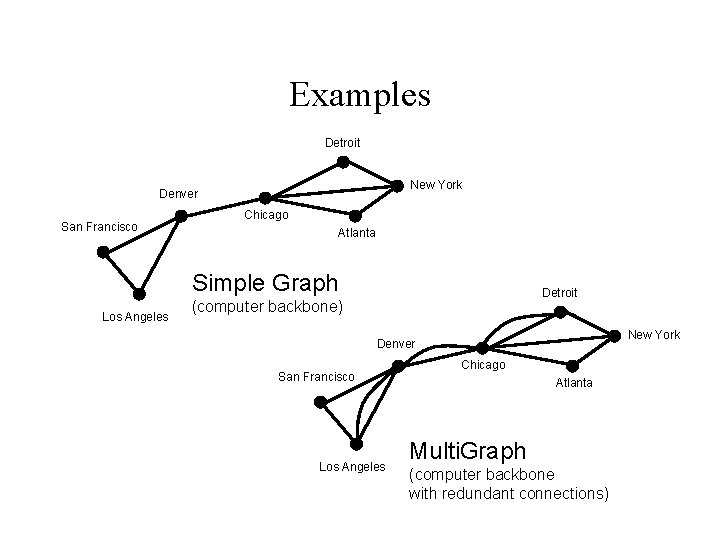
Examples Detroit New York Denver San Francisco Chicago Atlanta Simple Graph Los Angeles Detroit (computer backbone) New York Denver San Francisco Los Angeles Chicago Atlanta Multi. Graph (computer backbone with redundant connections)

Directed Graph • A directed graph consists of a set of vertices V and a set of edges E that are ordered pairs of V – Loops are allowed – Multiple edges are allowed 4 1 Digraph for equivalence relation on {1, 4, 7} 7

Adjacency and Degree • Two vertices u and v in an undirected graph are called adjacent (or neighbors) in G if e = {u, v} is an edge of G. The edge e is said to connect u and v. The vertices u and v are called the endpoints of e. • The degree of a vertex in an undirected graph is the number of edges that are incident with (or connect) it, except that a loop at a vertex contributes twice to the degree. The degree of the vertex v is denoted by deg(v).

Handshaking Theorem Let G = (V, E) be an undirected graph with e edges. Then (Note that this applies even if multiple edges and loops are present. )

How many edges are there in a graph with ten vertices each of degree 6? Since the sum of the degrees of the vertices is 6· 10 = 60, it follows that 2 e =60. Therefore, e = 30.

Prove that an undirected graph has an even number of vertices of odd degree. Let V 1 and V 2 be the set of vertices of even degree and the set of vertices of odd degree, respectively, in an undirected graph G = (V, E). Then Since deg(v) is even for v V 1, this term is even.

Prove that an undirected graph has an even number of vertices of odd degree. Furthermore, the sum of these two terms is even, since the sum is 2 e. Hence, the second term in the sum is also even. (Why? ) Since all the terms in the sum are odd, there must be an even number of such terms. (Why? ) Thus there an even number of vertices of odd degree. What can we say about the vertices of even degree?

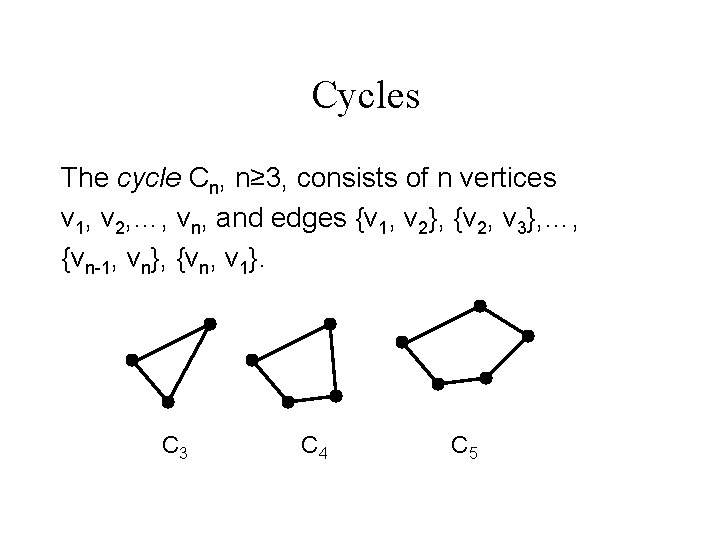
Cycles The cycle Cn, n≥ 3, consists of n vertices v 1, v 2, …, vn, and edges {v 1, v 2}, {v 2, v 3}, …, {vn-1, vn}, {vn, v 1}. C 3 C 4 C 5

Tree A circuit is a path of edges that begins and ends at the same vertex. A path or circuit is simple if it does not contain the same edge more than once. • A tree is a connected undirected graph with no simple circuits. • A forest is a set of trees that are not connected.

Example: Quadtree Q Q Q Linked Global Quadtrees Q Q Q Q

Example: Quadtree Q Q Q Linked Global Quadtrees Regular Triangularization (128 x 128 grid points) Q Q Q Q } 22 levels

Quadtree: Terrain Global Terrain (elevation & imagery) • Multiresolution • Scalable (multiple terabyte databases) • Efficient (100 to 1 or more reduction)

View-Dependent Simplification

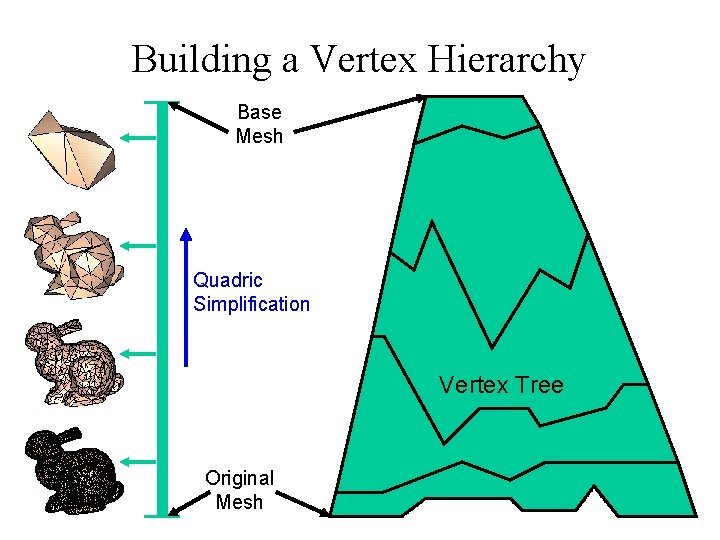
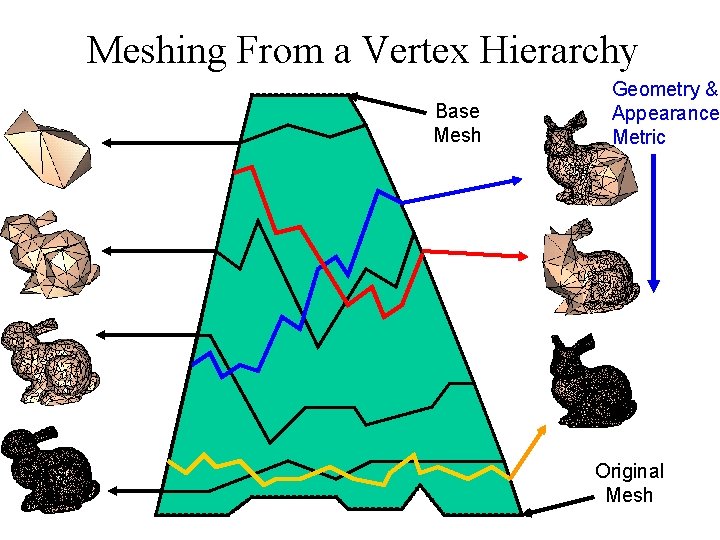
Building a Vertex Hierarchy Base Mesh Quadric Simplification Vertex Tree Original Mesh

Meshing From a Vertex Hierarchy Base Mesh Geometry & Appearance Metric Original Mesh