Graphs Part I Shannon Quinn with thanks to




















































![Co. EM/HF/wv. RN • One definition [Mac. Skassy & Provost, JMLR 2007]: … Co. EM/HF/wv. RN • One definition [Mac. Skassy & Provost, JMLR 2007]: …](https://slidetodoc.com/presentation_image_h/04317a7b786b4db360c7501d39b17cdc/image-80.jpg)

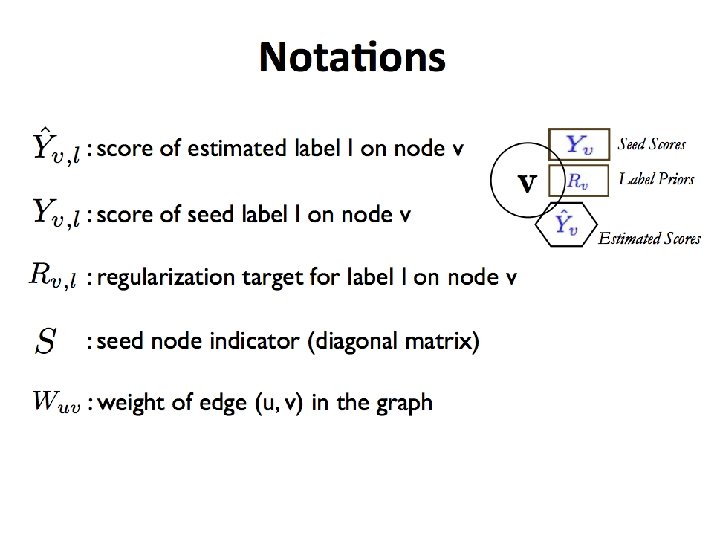




- Slides: 93

Graphs (Part I) Shannon Quinn (with thanks to William Cohen of CMU and Jure Leskovec, Anand Rajaraman, and Jeff Ullman of Stanford University)

Why I’m talking about graphs • Lots of large data is graphs – Facebook, Twitter, citation data, and other social networks – The web, the blogosphere, the semantic web, Freebase, Wikipedia, Twitter, and other information networks – Text corpora (like RCV 1), large datasets with discrete feature values, and other bipartite networks • nodes = documents or words • links connect document word or word document – Computer networks, biological networks (proteins, ecosystems, brains, …), … – Heterogeneous networks with multiple types of nodes • people, groups, documents

Properties of Graphs Descriptive Statistics • Number of connected components • Diameter • Degree distribution • … Models of Growth/Formation • Erdos-Renyi • Preferential attachment • Stochastic block models • …. Let’s look at some examples of graphs … but first, why are these statistics important?

An important question • How do you explore a dataset? – compute statistics (e. g. , feature histograms, conditional feature histograms, correlation coefficients, …) – sample and inspect • run a bunch of small-scale experiments • How do you explore a graph? – compute statistics (degree distribution, …) – sample and inspect • how do you sample?

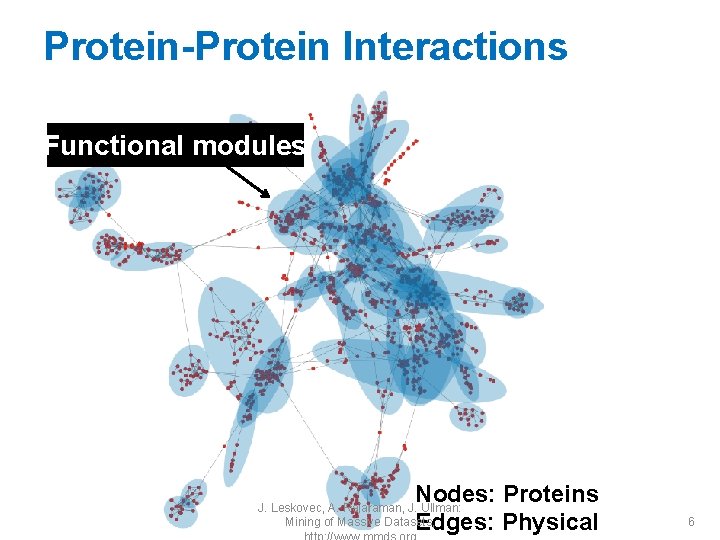
Protein-Protein Interactions Can we identify functional modules? Nodes: Proteins Edges: Physical J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, 5

Protein-Protein Interactions Functional modules Nodes: Proteins Edges: Physical J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, 6

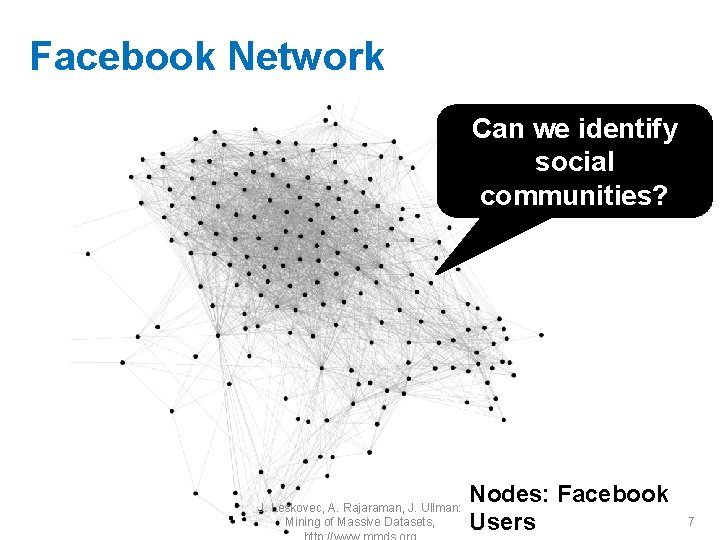
Facebook Network Can we identify social communities? J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, Nodes: Facebook Users 7

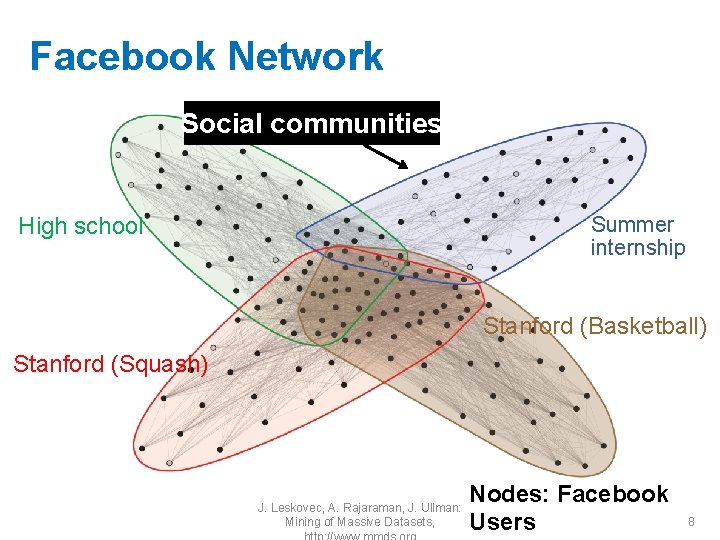
Facebook Network Social communities Summer internship High school Stanford (Basketball) Stanford (Squash) J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, Nodes: Facebook Users 8

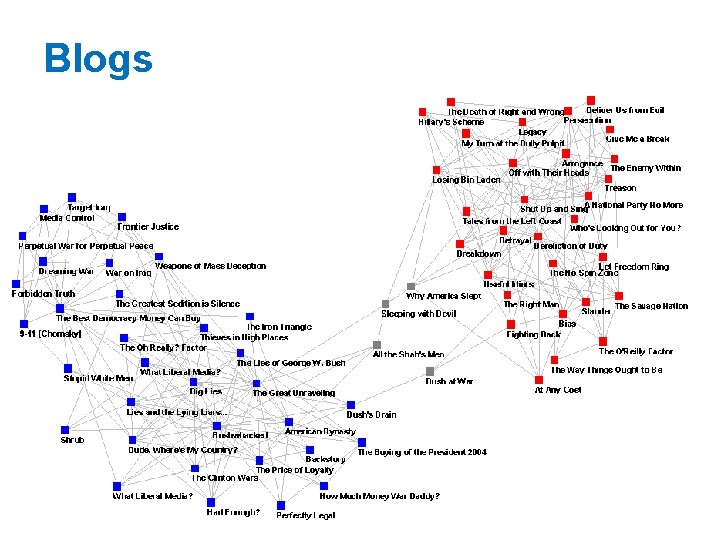
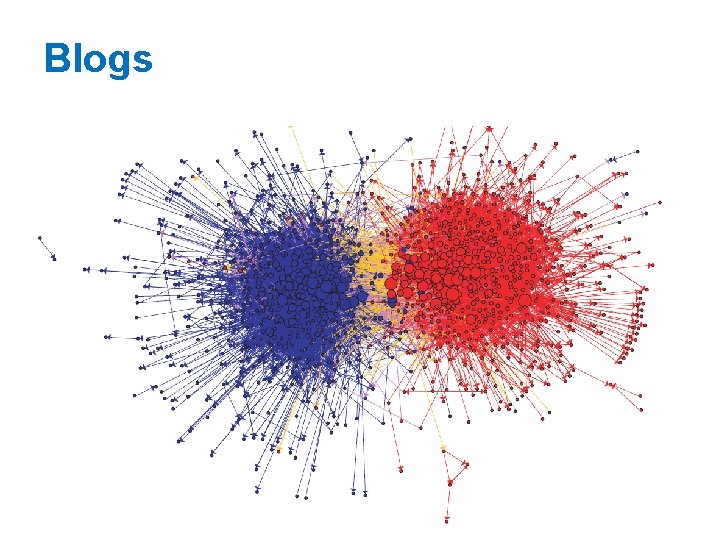
Blogs

Citations

Blogs

Blogs

Graphs • Set V of vertices/nodes v 1, … , set E of edges (u, v), …. – Edges might be directed and/or weighted and/or labeled • Degree of v is #edges touching v – Indegree and Outdegree for directed graphs • Path is sequence of edges (v 0, v 1), (v 1, v 2), …. • Geodesic path between u and v is shortest path connecting them – Diameter is max u, v in V {length of geodesic between u, v} – Effective diameter is 90 th percentile – Mean diameter is over connected pairs • (Connected) component is subset of nodes that are all pairwise connected via paths • Clique is subset of nodes that are all pairwise connected via edges • Triangle is a clique of size three

Graphs • Some common properties of graphs: – Distribution of node degrees – Distribution of cliques (e. g. , triangles) – Distribution of paths • Diameter (max shortest-path) • Effective diameter (90 th percentile) • Connected components – … • Some types of graphs to consider: – Real graphs (social & otherwise) – Generated graphs: • Erdos-Renyi “Bernoulli” or “Poisson” • Watts-Strogatz “small world” graphs • Barbosi-Albert “preferential attachment” • …

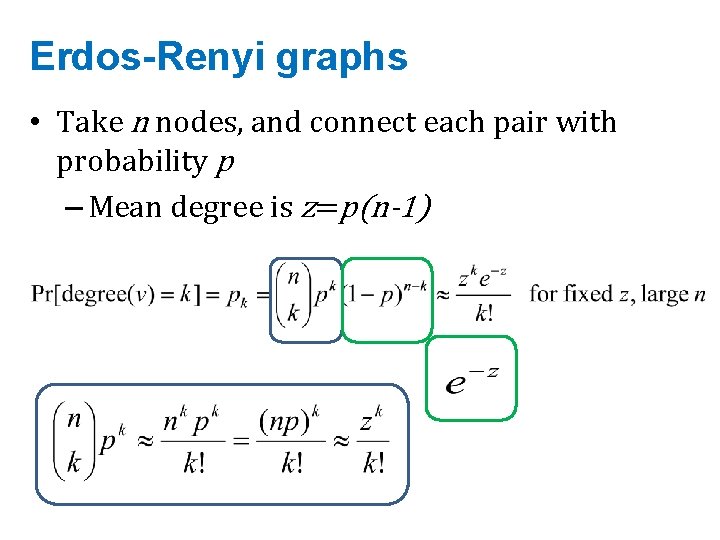
Erdos-Renyi graphs • Take n nodes, and connect each pair with probability p – Mean degree is z=p(n-1)

Erdos-Renyi graphs • Take n nodes, and connect each pair with probability p – Mean degree is z=p(n-1) – Mean number of neighbors distance d from v is zd – How large does d need to be so that zd >=n ? • If z>1, d = log(n)/log(z) • If z<1, you can’t do it – So: • There tend to be either many small components (z<1) or one large one (z>1) giant connected component) – Another intuition: • If there a two large connected components, then with high probability a few random edges will link them up.

Erdos-Renyi graphs • Take n nodes, and connect each pair with probability p – Mean degree is z=p(n-1) – Mean number of neighbors distance d from v is zd – How large does d need to be so that zd >=n ? • If z>1, d = log(n)/log(z) • If z<1, you can’t do it – So: • If z>1, diameters tend to be small (relative to n)

Sociometry, Vol. 32, No. 4. (Dec. , 1969), pp. 425 -443. 64 of 296 chains succeed, avg chain length is 6. 2

Illustrations of the Small World • Millgram’s experiment • Erdős numbers – http: //www. ams. org/mathscinet/searchauthors. html • Bacon numbers – http: //oracleofbacon. org/ • Linked. In – http: //www. linkedin. com/ – Privacy issues: the whole network is not visible to all


Erdos-Renyi graphs • Take n nodes, and connect each pair with probability p – Mean degree is z=p(n-1) This is usually not a good model of degree distribution in natural networks

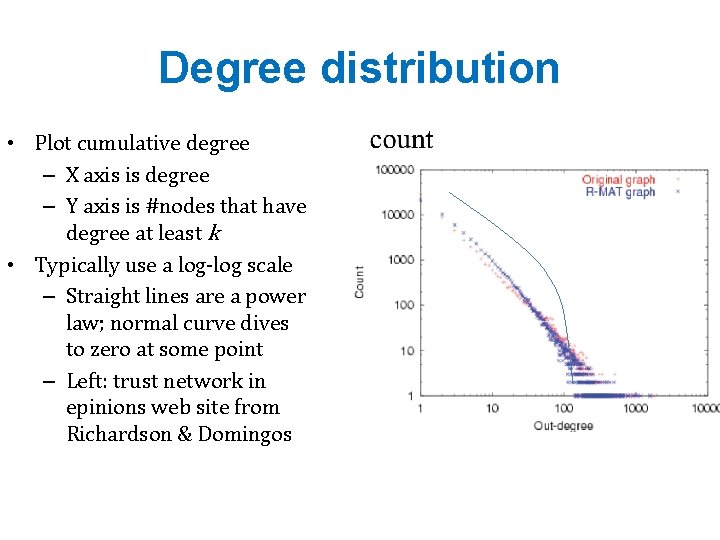
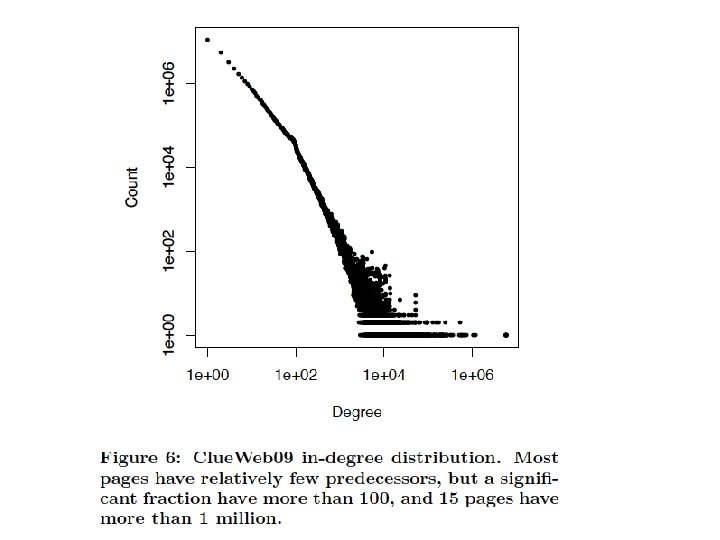
Degree distribution • Plot cumulative degree – X axis is degree – Y axis is #nodes that have degree at least k • Typically use a log-log scale – Straight lines are a power law; normal curve dives to zero at some point – Left: trust network in epinions web site from Richardson & Domingos

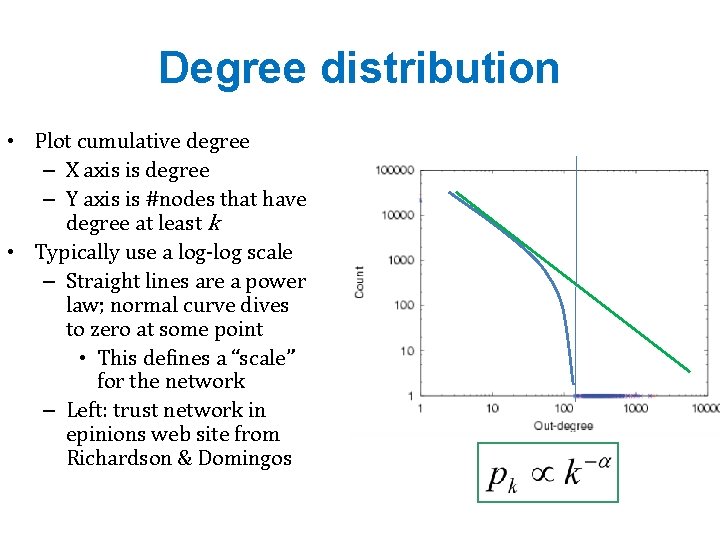
Degree distribution • Plot cumulative degree – X axis is degree – Y axis is #nodes that have degree at least k • Typically use a log-log scale – Straight lines are a power law; normal curve dives to zero at some point • This defines a “scale” for the network – Left: trust network in epinions web site from Richardson & Domingos

Graphs • Some common properties of graphs: – Distribution of node degrees – Distribution of cliques (e. g. , triangles) – Distribution of paths • Diameter (max shortest-path) • Effective diameter (90 th percentile) • Connected components – … • Some types of graphs to consider: – Real graphs (social & otherwise) – Generated graphs: • Erdos-Renyi “Bernoulli” or “Poisson” • Watts-Strogatz “small world” graphs • Barbosi-Albert “preferential attachment” • …

Graphs • Some common properties of graphs: – Distribution of node degrees: often scale-free – Distribution of cliques (e. g. , triangles) – Distribution of paths • Diameter (max shortestpath) • Effective diameter (90 th percentile) often small • Connected components usually one giant CC – … • Some types of graphs to consider: – Real graphs (social & otherwise) – Generated graphs: • Erdos-Renyi “Bernoulli” or “Poisson” • Watts-Strogatz “small world” graphs • Barbosi-Albert “preferential attachment” generates scale-free graphs • …

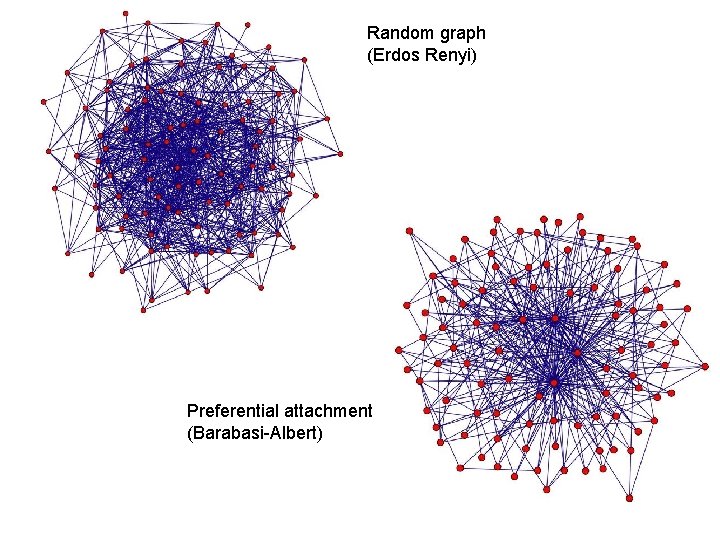
Barabasi-Albert Networks • Science 286 (1999) • Start from a small number of node, add a new node with m links • Preferential Attachment • Probability of these links to connect to existing nodes is proportional to the node’s degree • ‘Rich gets richer’ • This creates ‘hubs’: few nodes with very large degrees

Random graph (Erdos Renyi) Preferential attachment (Barabasi-Albert)

Graphs • Some common properties of graphs: – Distribution of node degrees: often scale-free – Distribution of cliques (e. g. , triangles) – Distribution of paths • Diameter (max shortestpath) • Effective diameter (90 th percentile) often small • Connected components usually one giant CC – … • Some types of graphs to consider: – Real graphs (social & otherwise) – Generated graphs: • Erdos-Renyi “Bernoulli” or “Poisson” • Watts-Strogatz “small world” graphs • Barbosi-Albert “preferential attachment” generates scale-free graphs • …

Homophily • One definition: excess edges between similar nodes – E. g. , assume nodes are male and female and Pr(male)=p, Pr(female)=q. – Is Pr(gender(u)≠ gender(v) | edge (u, v)) >= 2 pq? • Another def’n: excess edges between common neighbors of v

Homophily • Another def’n: excess edges between common neighbors of v

Homophily • In a random Erdos-Renyi graph: In natural graphs two of your mutual friends might well be friends: • Like you they are both in the same class (club, field of CS, …) • You introduced them

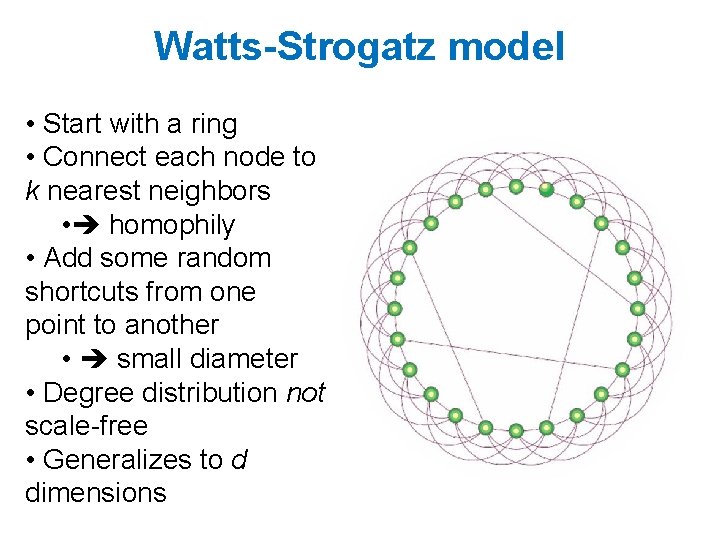
Watts-Strogatz model • Start with a ring • Connect each node to k nearest neighbors • homophily • Add some random shortcuts from one point to another • small diameter • Degree distribution not scale-free • Generalizes to d dimensions

An important question • How do you explore a dataset? – compute statistics (e. g. , feature histograms, conditional feature histograms, correlation coefficients, …) – sample and inspect • run a bunch of small-scale experiments • How do you explore a graph? – compute statistics (degree distribution, …) – sample and inspect • how do you sample?

KDD 2006

Brief summary • Define goals of sampling: – “scale-down” – find G’<G with similar statistics – “back in time”: for a growing G, find G’<G that is similar (statistically) to an earlier version of G • Experiment on real graphs with plausible sampling methods, such as – RN – random nodes, sampled uniformly –… • See how well they perform

Brief summary • Experiment on real graphs with plausible sampling methods, such as – RN – random nodes, sampled uniformly • RPN – random nodes, sampled by Page. Rank • RDP – random nodes sampled by in-degree – RE – random edges – RJ – run Page. Rank’s “random surfer” for n steps – RW – run RWR’s “random surfer” for n steps – FF – repeatedly pick r(i) neighbors of i to “burn”, and then recursively sample from them

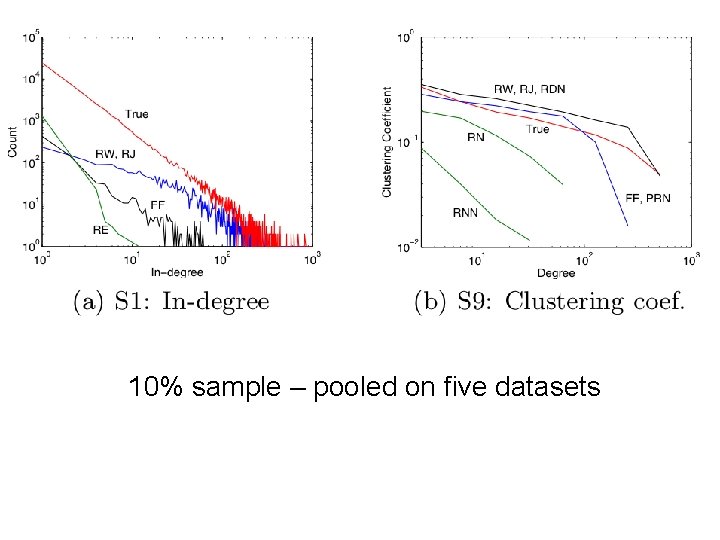
10% sample – pooled on five datasets

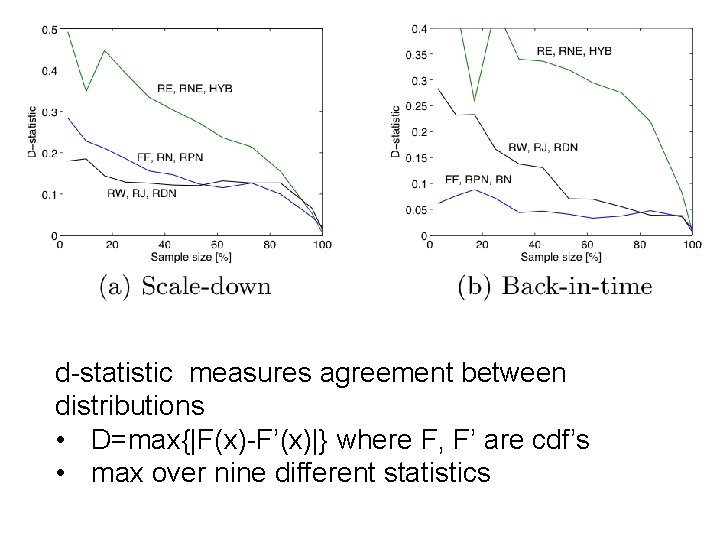
d-statistic measures agreement between distributions • D=max{|F(x)-F’(x)|} where F, F’ are cdf’s • max over nine different statistics

Parallel Graph Computation • Distributed computation and/or multicore parallelism – Sometimes confusing. We will talk mostly about distributed computation. • Are classic graph algorithms parallelizable? What about distributed? – Depth-first search? – Breadth-first search? – Priority-queue based traversals (Djikstra’s, Prim’s algorithms)

Map. Reduce for Graphs • Graph computation almost always iterative • Map. Reduce ends up shipping the whole graph on each iteration over the network (map>reduce->map->reduce->. . . ) – Mappers and reducers are stateless

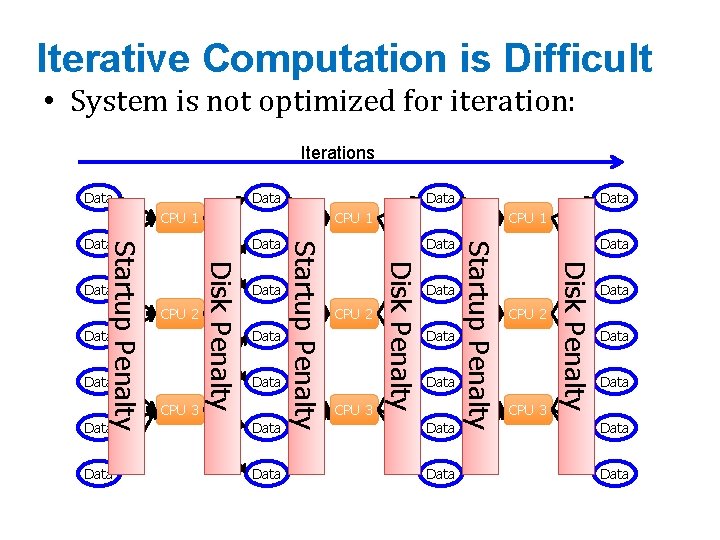
Iterative Computation is Difficult • System is not optimized for iteration: Iterations Data CPU 1 Data CPU 2 CPU 3 Data Data CPU 2 CPU 3 Disk Penalty CPU 3 Data Startup Penalty Data CPU 1 Disk Penalty Data Disk Penalty Startup Penalty CPU 2 Data Startup Penalty Data Data Data

Map. Reduce and Partitioning • Map-Reduce splits the keys randomly between mappers/reducers • But on natural graphs, high-degree vertices (keys) may have million-times more edges than the average Extremely uneven distribution Time of iteration = time of slowest job.

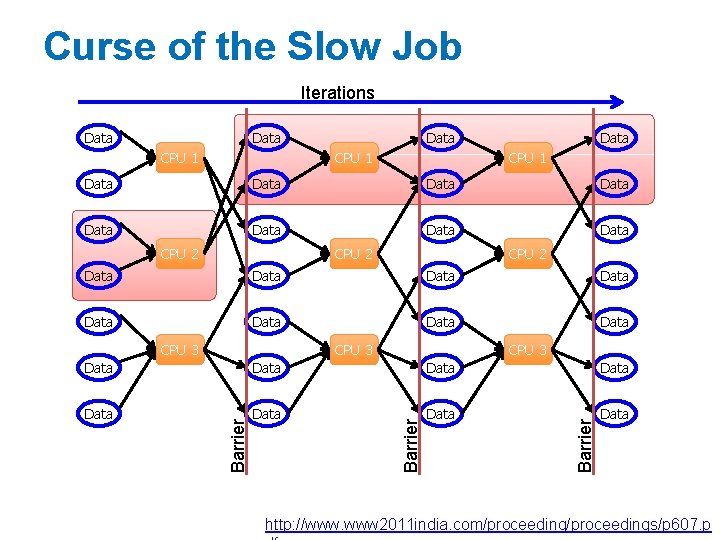
Curse of the Slow Job Iterations Data CPU 1 Data Data CPU 2 Data Data CPU 3 Data Data Barrier Data http: //www. www 2011 india. com/proceedings/p 607. p

Map-Reduce is Bulk-Synchronous Parallel • Bulk-Synchronous Parallel = BSP (Valiant, 80 s) – Each iteration sees only the values of previous iteration. – In linear systems literature: Jacobi iterations • Pros: – Simple to program – Maximum parallelism – Simple fault-tolerance • Cons: – Slower convergence – Iteration time = time taken by the slowest node

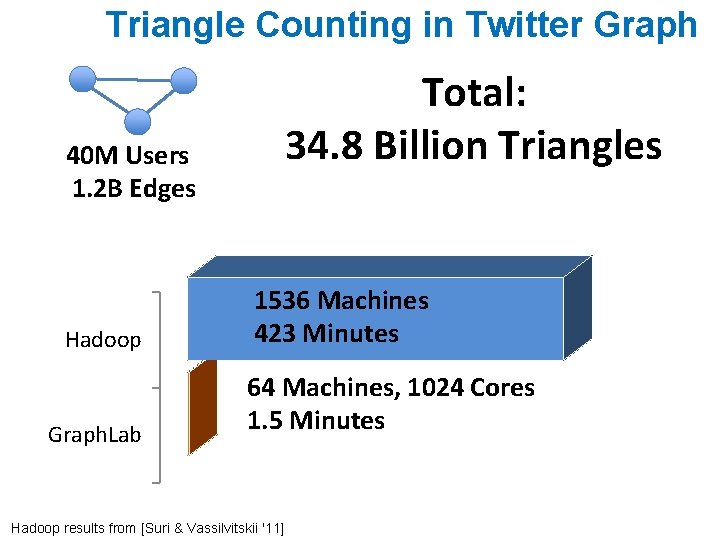
Triangle Counting in Twitter Graph Total: 34. 8 Billion Triangles 40 M Users 1. 2 B Edges Hadoop Graph. Lab 1536 Machines 423 Minutes 64 Machines, 1024 Cores 1. 5 Minutes Hadoop results from [Suri & Vassilvitskii '11]

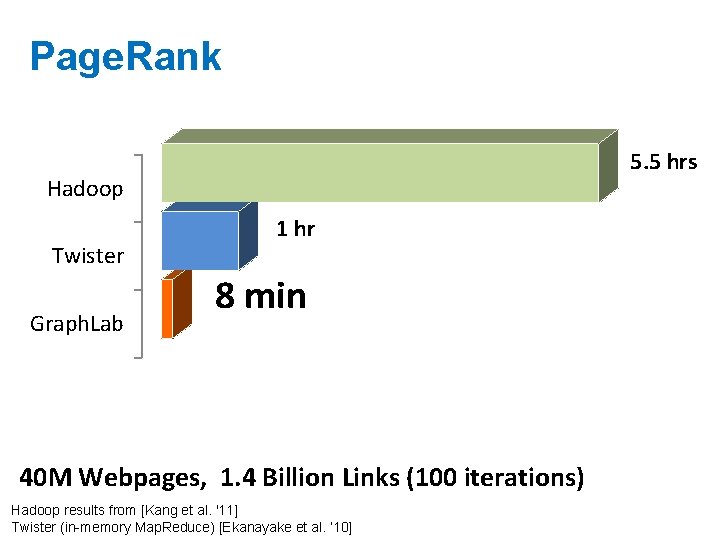
Page. Rank 5. 5 hrs Hadoop Twister Graph. Lab 1 hr 8 min 40 M Webpages, 1. 4 Billion Links (100 iterations) Hadoop results from [Kang et al. '11] Twister (in-memory Map. Reduce) [Ekanayake et al. ‘ 10]

Graph algorithms • Page. Rank implementations – in memory – streaming, node list in memory – streaming, no memory – map-reduce • A little like Naïve Bayes variants – data in memory – word counts in memory – stream-and-sort – map-reduce

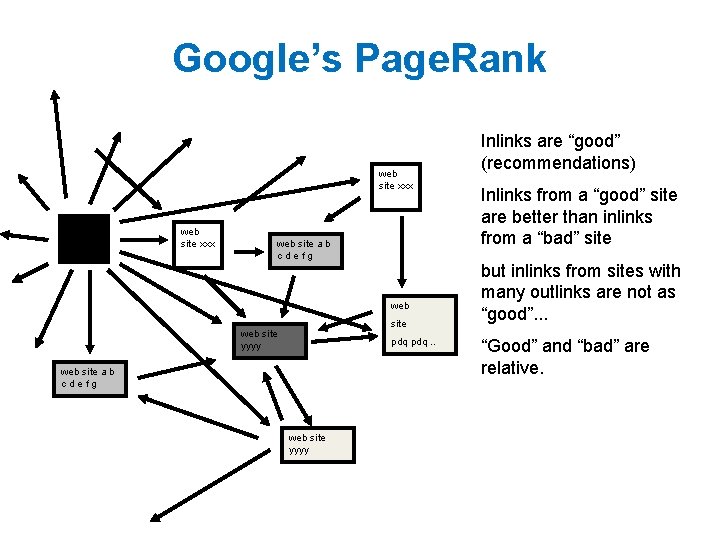
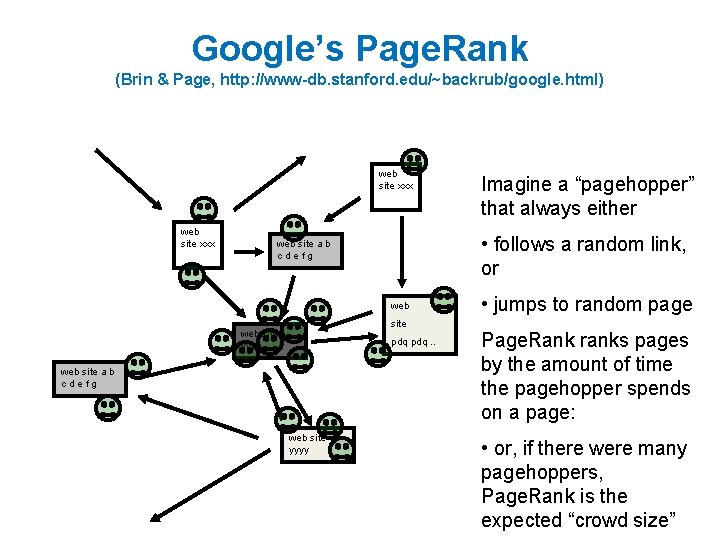
Google’s Page. Rank web site xxx web site a b cdefg web site yyyy pdq. . web site a b cdefg web site yyyy Inlinks are “good” (recommendations) Inlinks from a “good” site are better than inlinks from a “bad” site but inlinks from sites with many outlinks are not as “good”. . . “Good” and “bad” are relative.

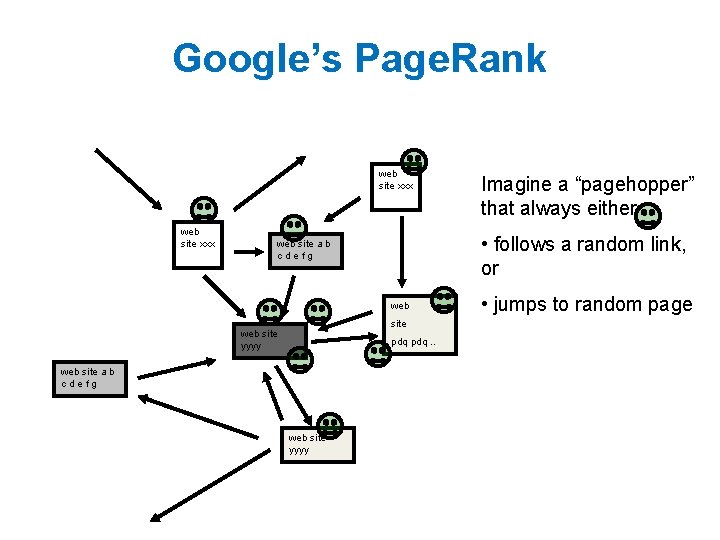
Google’s Page. Rank web site xxx • follows a random link, or web site a b cdefg web site yyyy pdq. . web site a b cdefg web site yyyy Imagine a “pagehopper” that always either • jumps to random page

Google’s Page. Rank (Brin & Page, http: //www-db. stanford. edu/~backrub/google. html) web site xxx • follows a random link, or web site a b cdefg web site yyyy pdq. . web site a b cdefg web site yyyy Imagine a “pagehopper” that always either • jumps to random page Page. Rank ranks pages by the amount of time the pagehopper spends on a page: • or, if there were many pagehoppers, Page. Rank is the expected “crowd size”

Random Walks avoids messy “dead ends”….

Random Walks: Page. Rank

Random Walks: Page. Rank

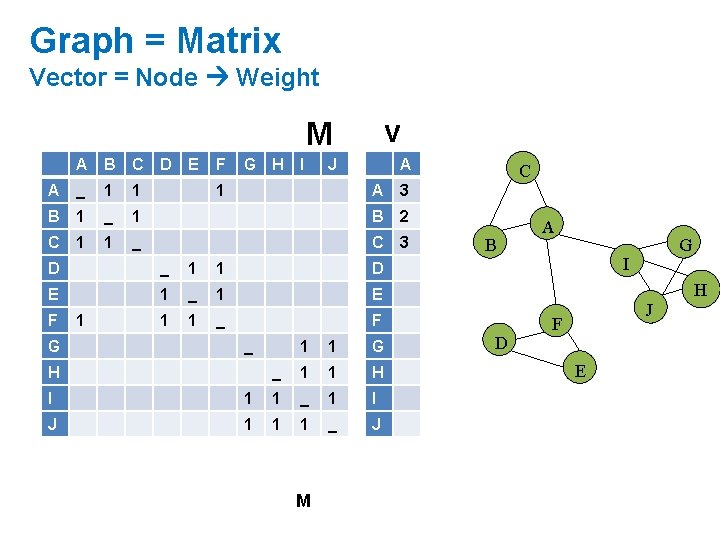
Graph = Matrix Vector = Node Weight v M A B C A _ 1 1 B 1 _ C 1 1 D E F G H I J 1 A A 3 1 B 2 _ C 3 D _ 1 1 D E 1 _ 1 E 1 1 _ F F G 1 _ H 1 1 G _ 1 1 H I 1 1 _ 1 I J 1 1 1 _ J M C B A G I H D J F E

Page. Rank in Memory • Let u = (1/N, …, 1/N) – dimension = #nodes N • Let A = adjacency matrix: [aij=1 i links to j] • Let W = [wij = aij/outdegree(i)] – wij is probability of jump from i to j • Let v 0 = (1, 1, …. , 1) – or anything else you want • Repeat until converged: – Let vt+1 = cu + (1 -c)Wvt • c is probability of jumping “anywhere randomly”

Streaming Page. Rank • Assume we can store v but not W in memory • Repeat until converged: – Let vt+1 = cu + (1 -c)Wvt • Store A as a row matrix: each line is – i ji, 1, …, ji, d [the neighbors of i] • Store v’ and v in memory: v’ starts out as cu • For each line “i ji, 1, …, ji, d “ – For each j in ji, 1, …, ji, d Everything needed for update is right • v’[j] += (1 -c)v[i]/d there in row….

Streaming Page. Rank: with some long rows • Repeat until converged: – Let vt+1 = cu + (1 -c)Wvt • Store A as a list of edges: each line is: “i d(i) j” • Store v’ and v in memory: v’ starts out as cu • For each line “i d j“ • v’[j] += (1 -c)v[i]/d We need to get the degree of i and store it locally

Streaming Page. Rank: preprocessing • • Original encoding is edges (i, j) Mapper replaces i, j with i, 1 Reducer is a Sum. Reducer Result is pairs (i, d(i)) • Then: join this back with edges (i, j) • For each i, j pair: – send j as a message to node i in the degree table • messages always sorted after non-messages – the reducer for the degree table sees i, d(i) first • then j 1, j 2, …. • can output the key, value pairs with key=i, value=d(i), j

Page. Rank in Map. Reduce

More on graph algorithms • Page. Rank is a one simple example of a graph algorithm – but an important one – personalized Page. Rank (aka “random walk with restart”) is an important operation in machine learning/data analysis settings • Page. Rank is typical in some ways – Trivial when graph fits in memory – Easy when node weights fit in memory – More complex to do with constant memory – A major expense is scanning through the graph many times • … same as with SGD/Logistic regression • disk-based streaming is much more expensive than memory-based approaches • Locality of access is very important! • gains if you can pre-cluster the graph even approximately • avoid sending messages across the network – keep them local

Machine Learning in Graphs - 2010

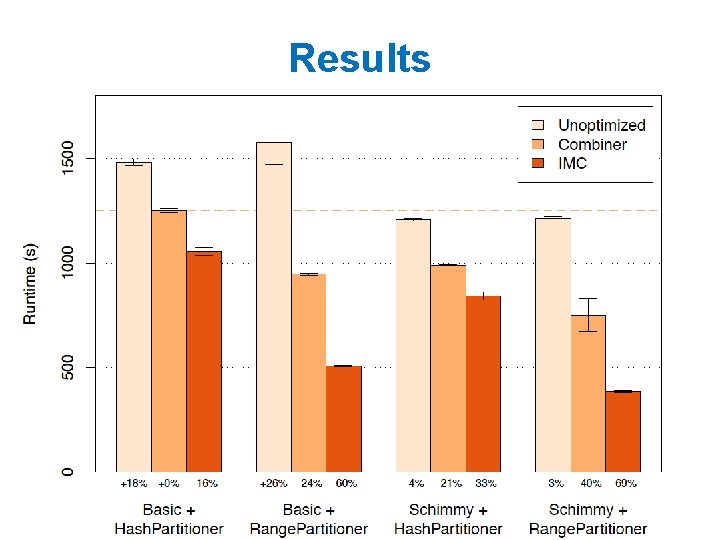
Some ideas • Combiners are helpful – Store outgoing increment. VBy messages and aggregate them – This is great for high indegree pages • Hadoop’s combiners are suboptimal – Messages get emitted before being combined – Hadoop makes weak guarantees about combiner usage

This slide again!



Some ideas • Most hyperlinks are within a domain – If we keep domains on the same machine this will mean more messages are local – To do this, build a custom partitioner that knows about the domain of each node. Id and keeps nodes on the same domain together – Assign node id’s so that nodes in the same domain are together – partition node ids by range – Change Hadoop’s Partitioner for this

Some ideas • Repeatedly shuffling the graph is expensive – We should separate the messages about the graph structure (fixed over time) from messages about page. Rank weights (variable) – compute and distribute the edges once – read them in incrementally in the reducer • not easy to do in Hadoop! – call this the “Schimmy” pattern

Schimmy Relies on fact that keys are sorted, and sorts the graph input the same way…. .

Schimmy

Results

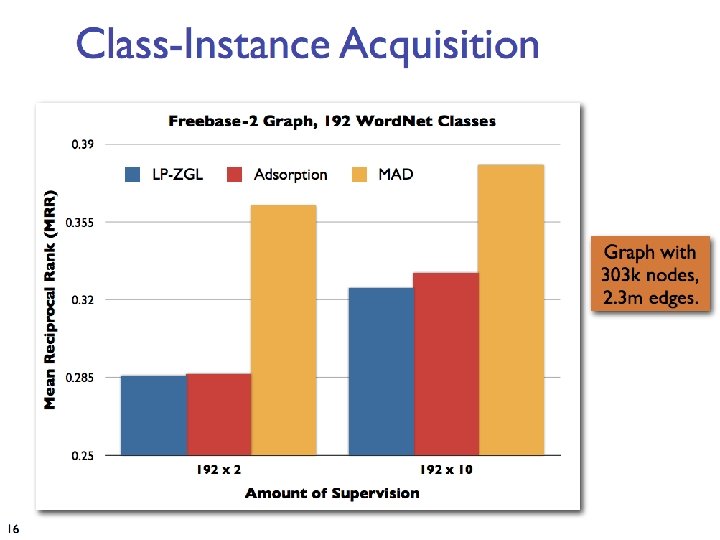
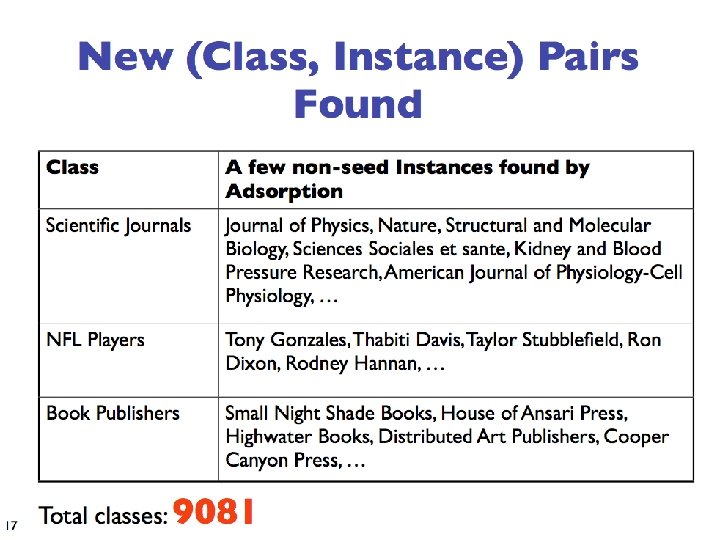
More details at… • Overlapping Community Detection at Scale: A Nonnegative Matrix Factorization Approach by J. Yang, J. Leskovec. ACM International Conference on Web Search and Data Mining (WSDM), 2013. • Detecting Cohesive and 2 -mode Communities in Directed and Undirected Networks by J. Yang, J. Mc. Auley, J. Leskovec. ACM International Conference on Web Search and Data Mining (WSDM), 2014. • Community Detection in Networks with Node Attributes by J. Yang, J. Mc. Auley, J. Leskovec. IEEE International Conference On Data Mining (ICDM), 2013. J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, 71

Semi-Supervised Learning With Graphs Shannon Quinn (with thanks to William Cohen at CMU)

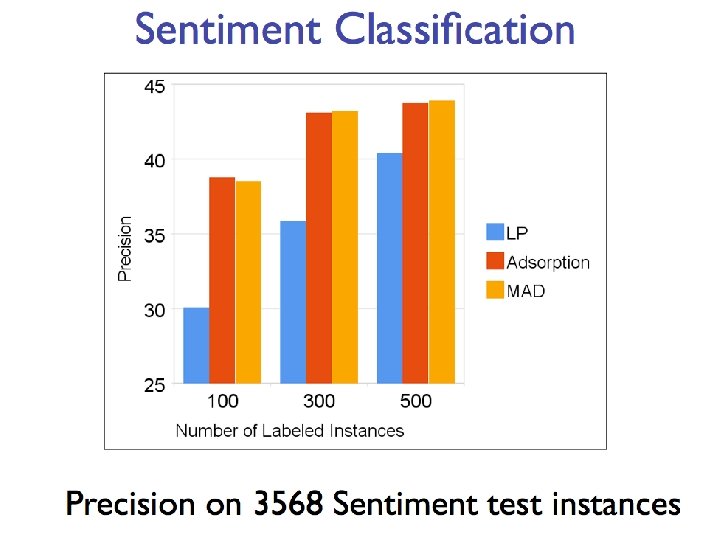
Semi-supervised learning • A pool of labeled examples L • A (usually larger) pool of unlabeled examples U • Can you improve accuracy somehow using U?

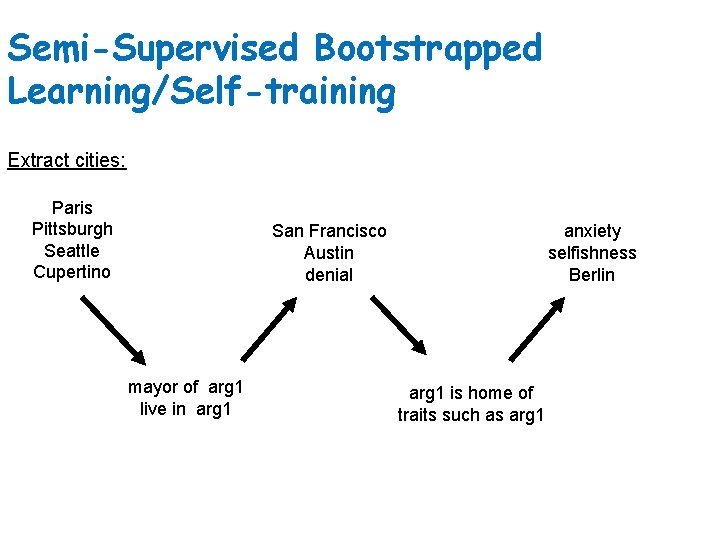
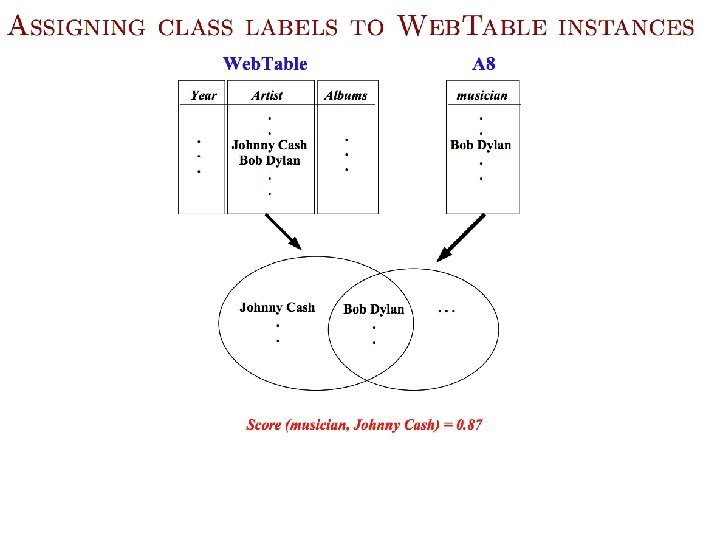
Semi-Supervised Bootstrapped Learning/Self-training Extract cities: Paris Pittsburgh Seattle Cupertino San Francisco Austin denial mayor of arg 1 live in arg 1 anxiety selfishness Berlin arg 1 is home of traits such as arg 1

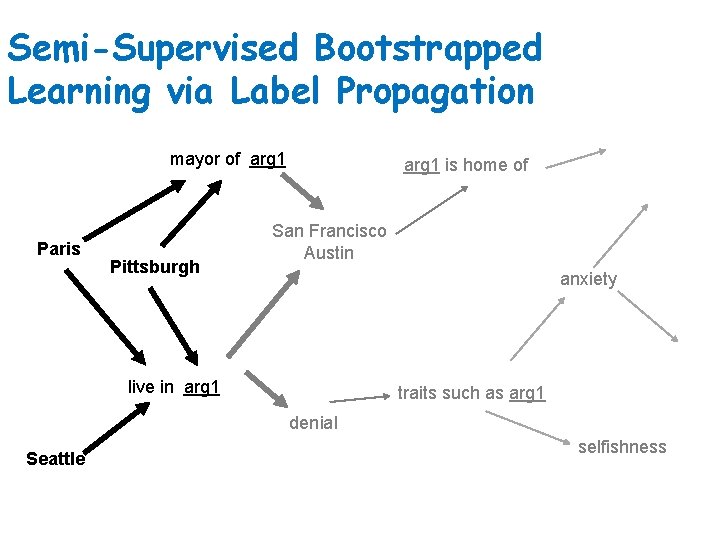
Semi-Supervised Bootstrapped Learning via Label Propagation mayor of arg 1 Paris Pittsburgh arg 1 is home of San Francisco Austin anxiety live in arg 1 traits such as arg 1 denial Seattle selfishness

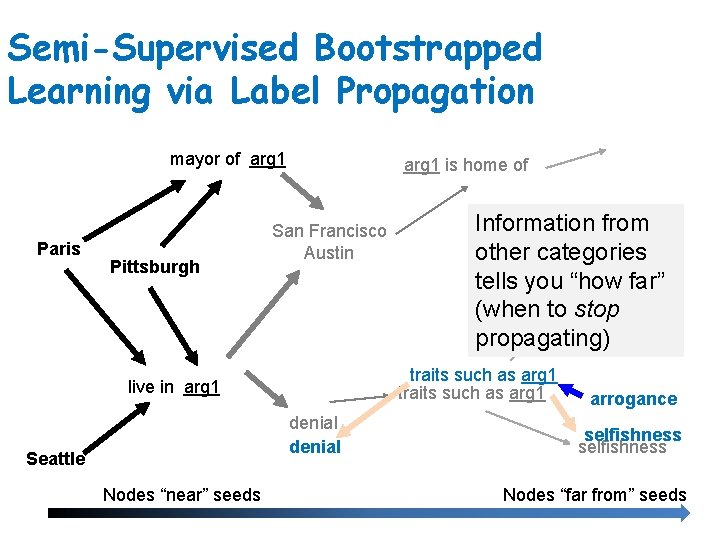
Semi-Supervised Bootstrapped Learning via Label Propagation mayor of arg 1 Paris Pittsburgh arg 1 is home of San Francisco Austin traits such as arg 1 live in arg 1 denial Seattle Nodes “near” seeds Information from other categories tells youanxiety “how far” (when to stop propagating) arrogance selfishness Nodes “far from” seeds

ASONAM-2010 (Advances in Social Networks Analysis and Mining)

Network Datasets with Known Classes • UBMCBlog • AGBlog • MSPBlog • Cora • Citeseer

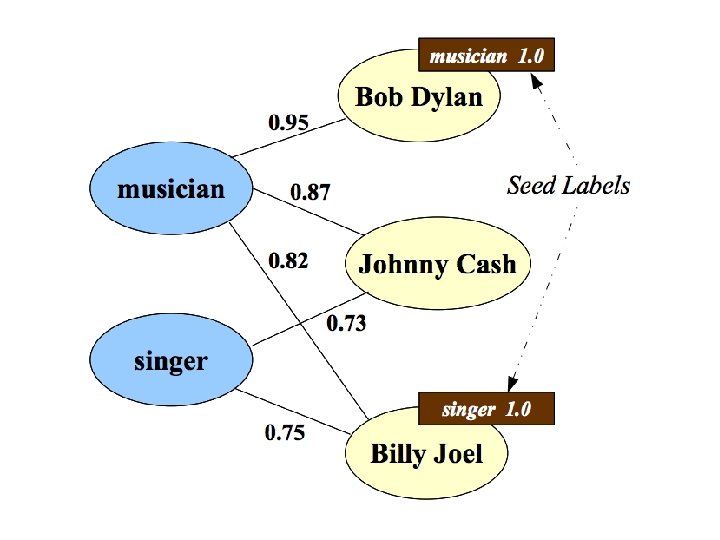
RWR - fixpoint of: Seed selection 1. order by Page. Rank, degree, or randomly 2. go down list until you have at least k examples/class
![Co EMHFwv RN One definition Mac Skassy Provost JMLR 2007 Co. EM/HF/wv. RN • One definition [Mac. Skassy & Provost, JMLR 2007]: …](https://slidetodoc.com/presentation_image_h/04317a7b786b4db360c7501d39b17cdc/image-80.jpg)
Co. EM/HF/wv. RN • One definition [Mac. Skassy & Provost, JMLR 2007]: …

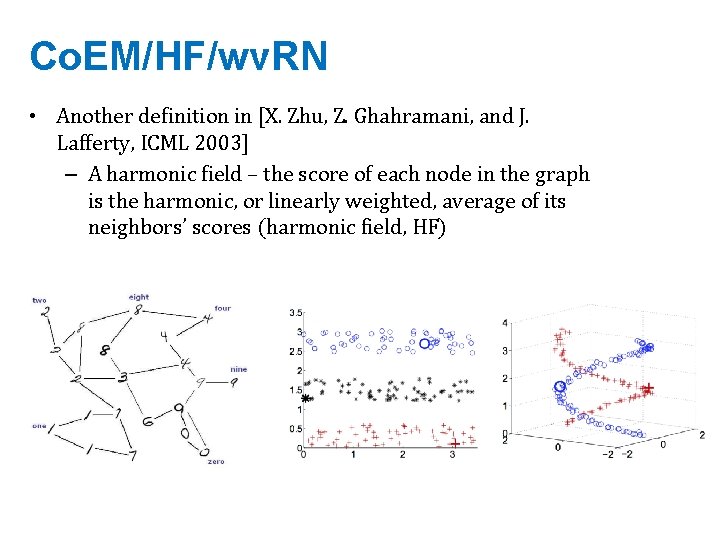
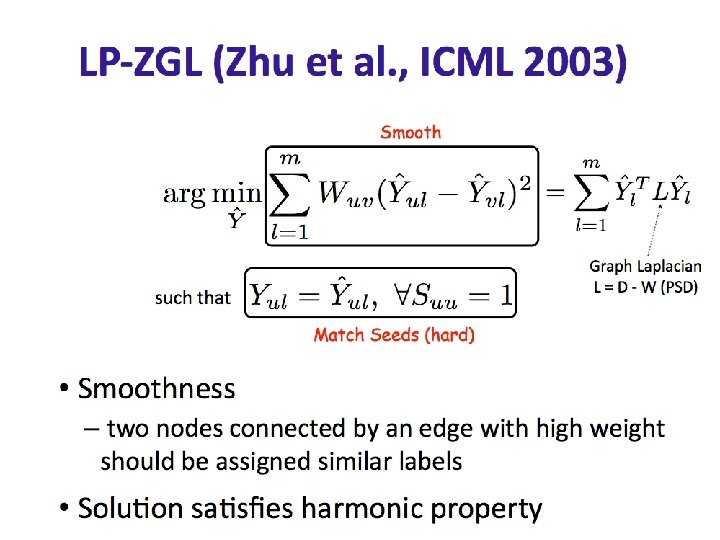
Co. EM/HF/wv. RN • Another definition in [X. Zhu, Z. Ghahramani, and J. Lafferty, ICML 2003] – A harmonic field – the score of each node in the graph is the harmonic, or linearly weighted, average of its neighbors’ scores (harmonic field, HF)

Co. EM/HF/wv. RN • Another justification of the same algorithm…. • … start with co -training with a naïve Bayes learner




How to do this minimization? First, differentiate to find min is at Jacobi method: • To solve Ax=b for x • Iterate: • … or:






