Graphs over Time Densification Laws Shrinking Diameters and




![School of Computer Science Carnegie Mellon n Small-world [Watts and Strogatz], ++: n 6 School of Computer Science Carnegie Mellon n Small-world [Watts and Strogatz], ++: n 6](https://slidetodoc.com/presentation_image_h/02d366d4048b00e15642b64b3d9679af/image-7.jpg)

















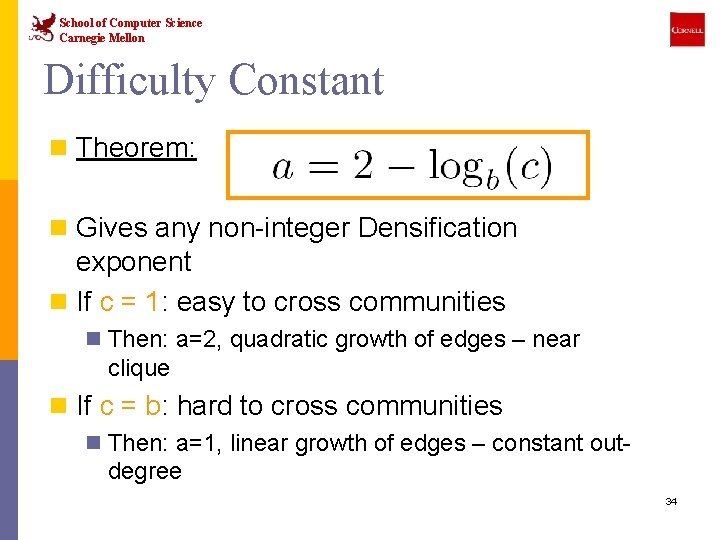















- Slides: 53

Graphs over Time Densification Laws, Shrinking Diameters and Possible Explanations Jurij Leskovec, CMU Jon Kleinberg, Cornell Christos Faloutsos, CMU 1

School of Computer Science Carnegie Mellon Introduction n What can we do with graphs? n What patterns or “laws” hold for most real-world graphs? n How do the graphs evolve over time? n Can we generate synthetic but “realistic” graphs? “Needle exchange” networks of drug users 2

School of Computer Science Carnegie Mellon Evolution of the Graphs n How do graphs evolve over time? n Conventional Wisdom: n Constant average degree: the number of edges grows linearly with the number of nodes n Slowly growing diameter: as the network grows the distances between nodes grow n Our findings: n Densification Power Law: networks are becoming denser over time n Shrinking Diameter: diameter is decreasing as the network grows 3

School of Computer Science Carnegie Mellon Outline n Introduction n General patterns and generators n Graph evolution – Observations n Densification Power Law n Shrinking Diameters n Proposed explanation n Community Guided Attachment n Proposed graph generation model n Forest Fire Model n Conclusion 4

School of Computer Science Carnegie Mellon Outline n Introduction n General patterns and generators n Graph evolution – Observations n Densification Power Law n Shrinking Diameters n Proposed explanation n Community Guided Attachment n Proposed graph generation model n Forest Fire Model n Conclusion 5

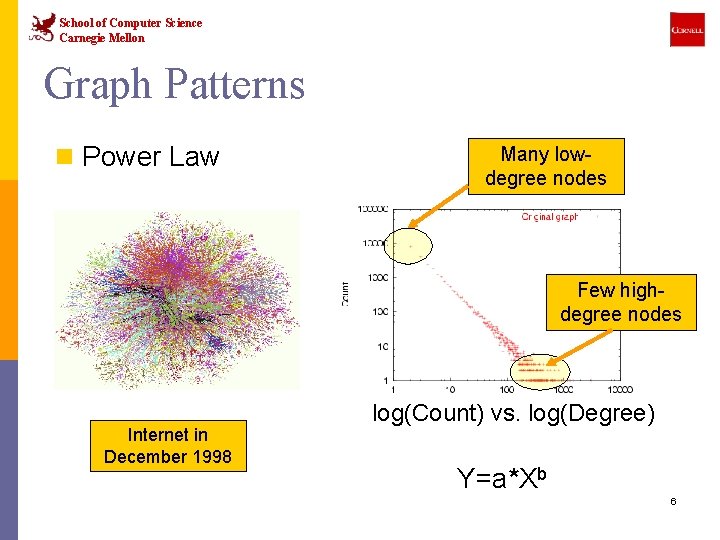
School of Computer Science Carnegie Mellon Graph Patterns n Power Law Many lowdegree nodes Few highdegree nodes Internet in December 1998 log(Count) vs. log(Degree) Y=a*Xb 6
![School of Computer Science Carnegie Mellon n Smallworld Watts and Strogatz n 6 School of Computer Science Carnegie Mellon n Small-world [Watts and Strogatz], ++: n 6](https://slidetodoc.com/presentation_image_h/02d366d4048b00e15642b64b3d9679af/image-7.jpg)
School of Computer Science Carnegie Mellon n Small-world [Watts and Strogatz], ++: n 6 degrees of separation n Small diameter n (Community # reachable pairs Graph Patterns Effective Diameter hops structure, …) 7

School of Computer Science Carnegie Mellon Graph models: Random Graphs n How can we generate a realistic graph? n given the number of nodes N and edges E n Random graph [Erdos & Renyi, 60 s]: n Pick 2 nodes at random and link them n Does not obey Power laws n No community structure 8

School of Computer Science Carnegie Mellon Graph models: Preferential attachment n Preferential attachment [Albert & Barabasi, 99]: n Add a new node, create M out-links n Probability of linking a node is proportional to its degree n Examples: n Citations: new citations of a paper are proportional to the number it already has n Rich get richer phenomena n Explains power-law degree distributions n But, all nodes have equal (constant) out-degree 9

School of Computer Science Carnegie Mellon Graph models: Copying model n Copying model [Kleinberg, Kumar, Raghavan, Rajagopalan and Tomkins, 99]: n Add a node and choose the number of edges to add n Choose a random vertex and “copy” its links (neighbors) n Generates power-law degree distributions n Generates communities 10

School of Computer Science Carnegie Mellon Other Related Work n Huberman and Adamic, 1999: Growth dynamics of the n n world wide web Kumar, Raghavan, Rajagopalan, Sivakumar and Tomkins, 1999: Stochastic models for the web graph Watts, Dodds, Newman, 2002: Identity and search in social networks Medina, Lakhina, Matta, and Byers, 2001: BRITE: An Approach to Universal Topology Generation … 11

School of Computer Science Carnegie Mellon Why is all this important? n Gives insight into the graph formation process: n Anomaly detection – abnormal behavior, evolution n Predictions – predicting future from the past n Simulations of new algorithms n Graph sampling – many real world graphs are too large to deal with 12

School of Computer Science Carnegie Mellon Outline n Introduction n General patterns and generators n Graph evolution – Observations n Densification Power Law n Shrinking Diameters n Proposed explanation n Community Guided Attachment n Proposed graph generation model n Forest Fire Model n Conclusion 13

School of Computer Science Carnegie Mellon Temporal Evolution of the Graphs n N(t) … nodes at time t n E(t) … edges at time t n Suppose that N(t+1) = 2 * N(t) n Q: what is your guess for E(t+1) =? 2 * E(t) n A: over-doubled! n But obeying the Densification Power Law 14

School of Computer Science Carnegie Mellon Temporal Evolution of the Graphs n Densification Power Law n networks are becoming denser over time n the number of edges grows faster than the number of nodes – average degree is increasing or equivalently a … densification exponent 15

School of Computer Science Carnegie Mellon Graph Densification – A closer look n Densification Power Law n Densification exponent: 1 ≤ a ≤ 2: n a=1: linear growth – constant out-degree (assumed in the literature so far) n a=2: quadratic growth – clique n Let’s see the real graphs! 16

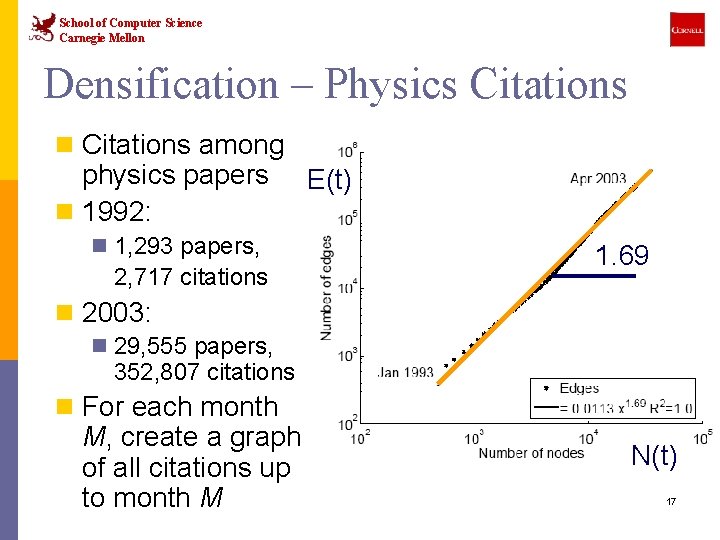
School of Computer Science Carnegie Mellon Densification – Physics Citations n Citations among physics papers n 1992: n 1, 293 papers, 2, 717 citations E(t) 1. 69 n 2003: n 29, 555 papers, 352, 807 citations n For each month M, create a graph of all citations up to month M N(t) 17

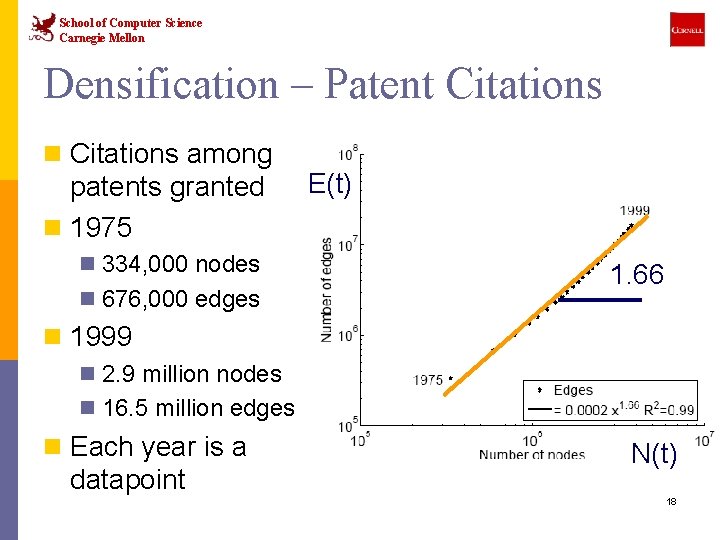
School of Computer Science Carnegie Mellon Densification – Patent Citations n Citations among patents granted n 1975 n 334, 000 nodes n 676, 000 edges E(t) 1. 66 n 1999 n 2. 9 million nodes n 16. 5 million edges n Each year is a datapoint N(t) 18

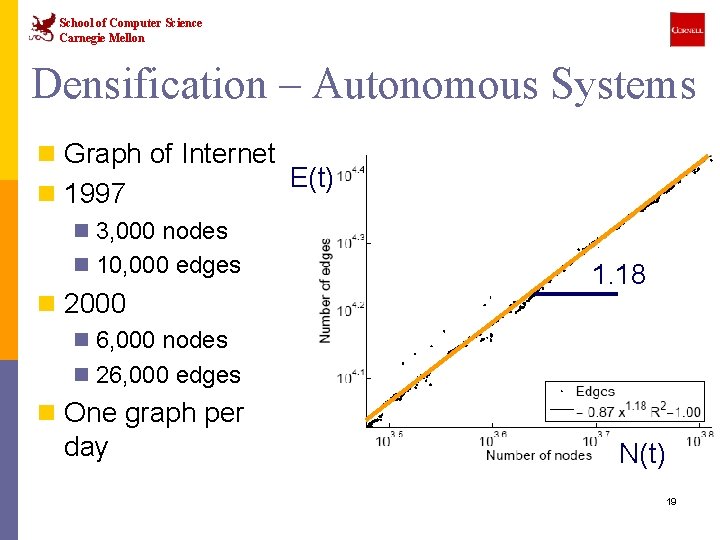
School of Computer Science Carnegie Mellon Densification – Autonomous Systems n Graph of Internet n 1997 E(t) n 3, 000 nodes n 10, 000 edges n 2000 1. 18 n 6, 000 nodes n 26, 000 edges n One graph per day N(t) 19

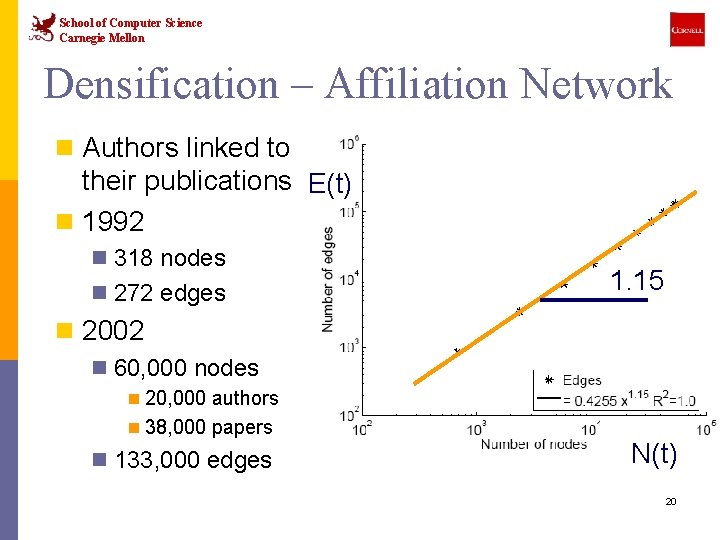
School of Computer Science Carnegie Mellon Densification – Affiliation Network n Authors linked to their publications E(t) n 1992 n 318 nodes n 272 edges 1. 15 n 2002 n 60, 000 nodes n 20, 000 authors n 38, 000 papers n 133, 000 edges N(t) 20

School of Computer Science Carnegie Mellon Graph Densification – Summary n The traditional constant out-degree assumption does not hold n Instead: n the number of edges grows faster than the number of nodes – average degree is increasing 21

School of Computer Science Carnegie Mellon Outline n Introduction n General patterns and generators n Graph evolution – Observations n Densification Power Law n Shrinking Diameters n Proposed explanation n Community Guided Attachment n Proposed graph generation model n Forest Fire Model n Conclusion 22

School of Computer Science Carnegie Mellon Evolution of the Diameter n Prior work on Power Law graphs hints at Slowly growing diameter: n diameter ~ O(log N) n What is happening in real data? n Diameter shrinks over time n As the network grows the distances between nodes slowly decrease 23

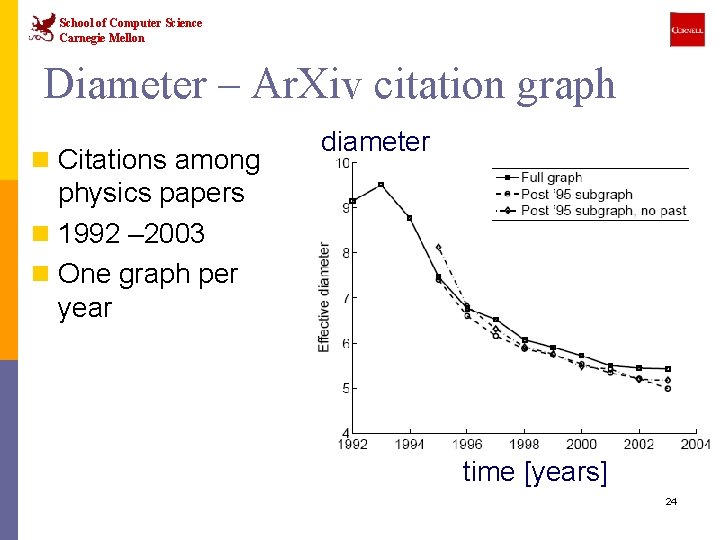
School of Computer Science Carnegie Mellon Diameter – Ar. Xiv citation graph n Citations among diameter physics papers n 1992 – 2003 n One graph per year time [years] 24

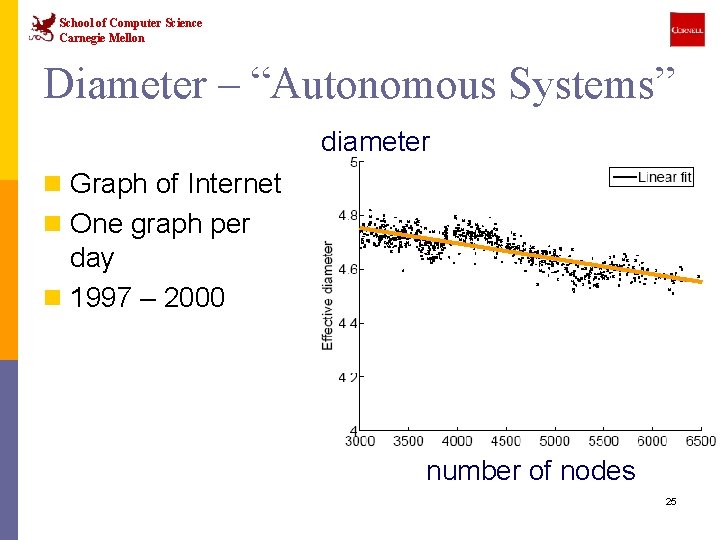
School of Computer Science Carnegie Mellon Diameter – “Autonomous Systems” diameter n Graph of Internet n One graph per day n 1997 – 2000 number of nodes 25

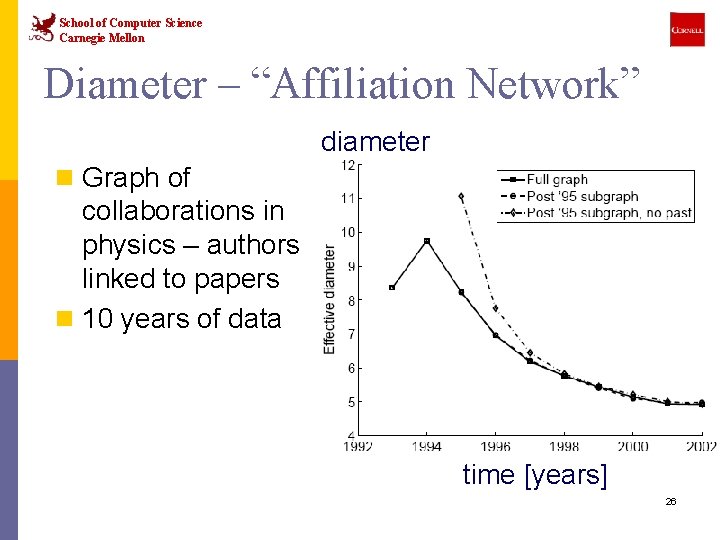
School of Computer Science Carnegie Mellon Diameter – “Affiliation Network” diameter n Graph of collaborations in physics – authors linked to papers n 10 years of data time [years] 26

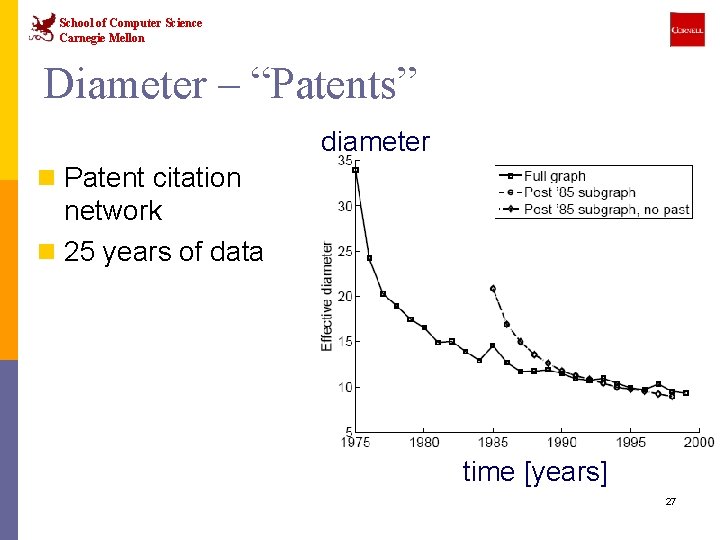
School of Computer Science Carnegie Mellon Diameter – “Patents” diameter n Patent citation network n 25 years of data time [years] 27

School of Computer Science Carnegie Mellon Validating Diameter Conclusions n There are several factors that could influence the Shrinking diameter n Effective Diameter: n Distance at which 90% of pairs of nodes is reachable n Problem of “Missing past” n How do we handle the citations outside the dataset? n Disconnected components n None of them matters 28

School of Computer Science Carnegie Mellon Outline n Introduction n General patterns and generators n Graph evolution – Observations n Densification Power Law n Shrinking Diameters n Proposed explanation n Community Guided Attachment n Proposed graph generation model n Forest Fire Mode n Conclusion 29

School of Computer Science Carnegie Mellon Densification – Possible Explanation n Existing graph generation models do not capture the Densification Power Law and Shrinking diameters n Can we find a simple model of local behavior, which naturally leads to observed phenomena? n Yes! We present 2 models: n Community Guided Attachment – obeys Densification n Forest Fire model – obeys Densification, Shrinking diameter (and Power Law degree distribution) 30

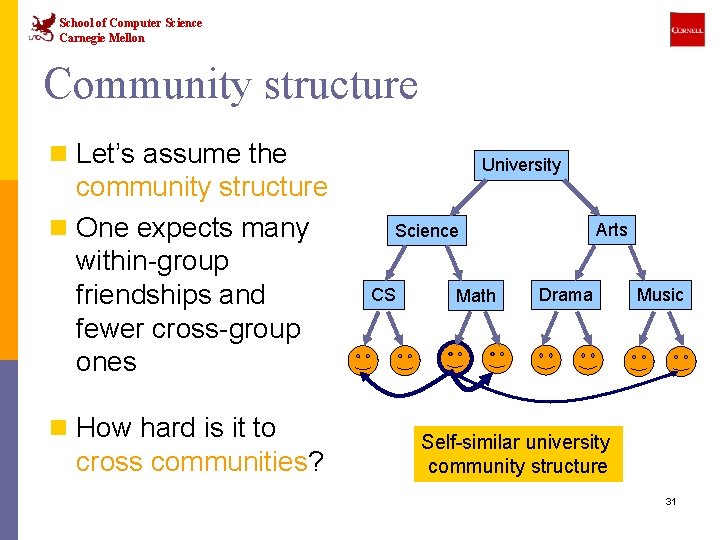
School of Computer Science Carnegie Mellon Community structure n Let’s assume the community structure n One expects many within-group friendships and fewer cross-group ones n How hard is it to cross communities? University Arts Science CS Math Drama Music Self-similar university community structure 31

School of Computer Science Carnegie Mellon Fundamental Assumption n If the cross-community linking probability of nodes at tree-distance h is scale-free n We propose cross-community linking probability: where: c ≥ 1 … the Difficulty constant h … tree-distance 32

School of Computer Science Carnegie Mellon Densification Power Law (1) n Theorem: The Community Guided Attachment leads to Densification Power Law with exponent n a … densification exponent n b … community structure branching factor n c … difficulty constant 33
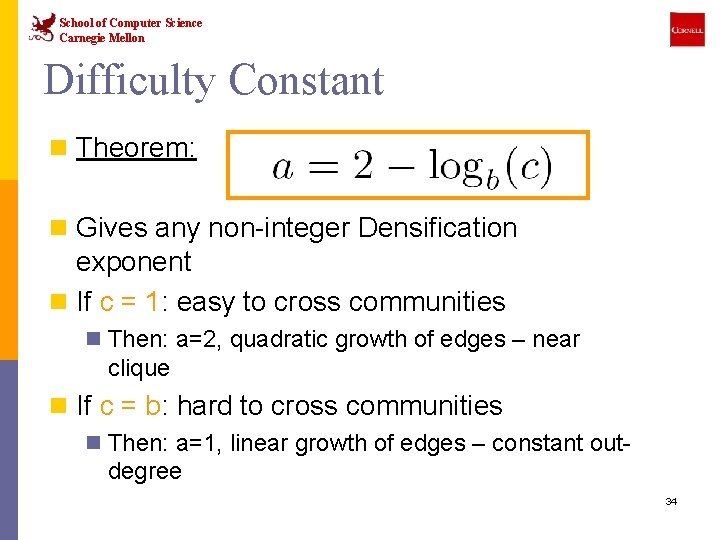
School of Computer Science Carnegie Mellon Difficulty Constant n Theorem: n Gives any non-integer Densification exponent n If c = 1: easy to cross communities n Then: a=2, quadratic growth of edges – near clique n If c = b: hard to cross communities n Then: a=1, linear growth of edges – constant out- degree 34

School of Computer Science Carnegie Mellon Room for Improvement n Community Guided Attachment explains Densification Power Law n Issues: n Requires explicit Community structure n Does not obey Shrinking Diameters 35

School of Computer Science Carnegie Mellon Outline n Introduction n General patterns and generators n Graph evolution – Observations n Densification Power Law n Shrinking Diameters n Proposed explanation n Community Guided Attachment n Proposed graph generation model n “Forest Fire” Model n Conclusion 36

School of Computer Science Carnegie Mellon “Forest Fire” model – Wish List n Want no explicit Community structure n Shrinking diameters n and: n “Rich get richer” attachment process, to get heavy- tailed in-degrees n “Copying” model, to lead to communities n Community Guided Attachment, to produce Densification Power Law 37

School of Computer Science Carnegie Mellon “Forest Fire” model – Intuition (1) n How do authors identify references? 1. Find first paper and cite it 2. Follow a few citations, make citations 3. Continue recursively 4. From time to time use bibliographic tools (e. g. Cite. Seer) and chase back-links 38

School of Computer Science Carnegie Mellon “Forest Fire” model – Intuition (2) n How do people make friends in a new environment? 1. 2. 3. 4. Find first a person and make friends Follow a of his friends Continue recursively From time to time get introduced to his friends n Forest Fire model imitates exactly this process 39

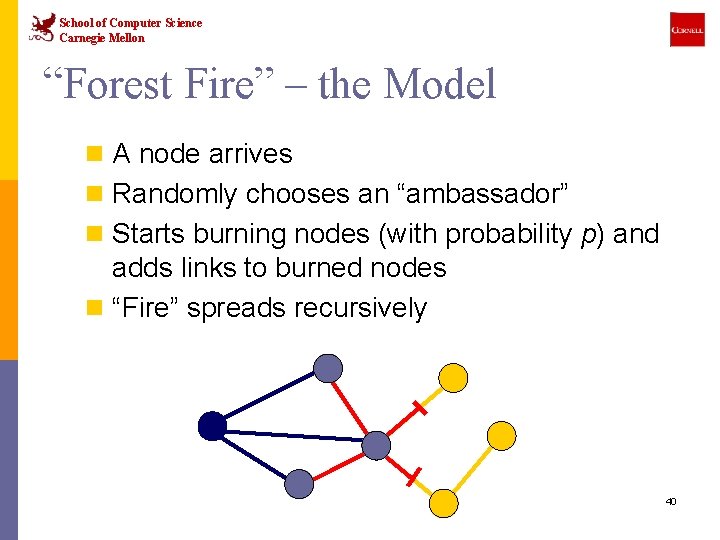
School of Computer Science Carnegie Mellon “Forest Fire” – the Model n A node arrives n Randomly chooses an “ambassador” n Starts burning nodes (with probability p) and adds links to burned nodes n “Fire” spreads recursively 40

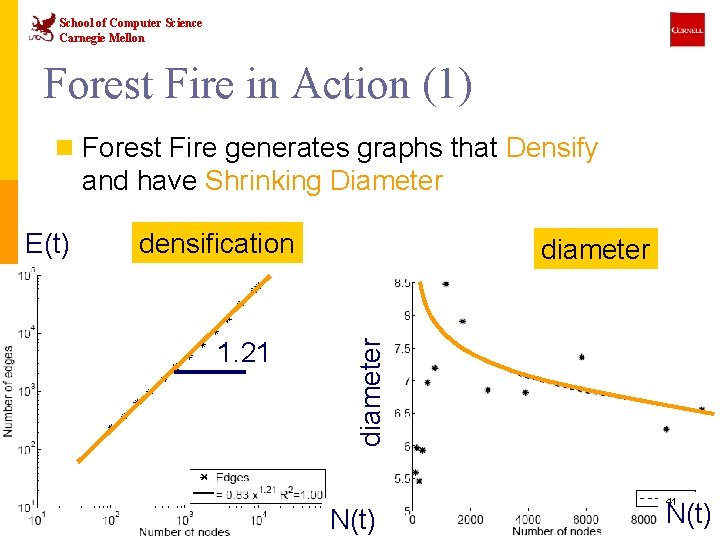
School of Computer Science Carnegie Mellon Forest Fire in Action (1) n Forest Fire generates graphs that Densify and have Shrinking Diameter densification 1. 21 diameter E(t) N(t) 41 N(t)

School of Computer Science Carnegie Mellon Forest Fire in Action (2) n Forest Fire also generates graphs with heavy-tailed degree distribution in-degree count vs. in-degree out-degree 42 count vs. out-degree

School of Computer Science Carnegie Mellon Forest Fire model – Justification n Densification Power Law: n Similar to Community Guided Attachment n The probability of linking decays exponentially with the distance – Densification Power Law n Power law out-degrees: n From time to time we get large fires n Power law in-degrees: n The fire is more likely to burn hubs 43

School of Computer Science Carnegie Mellon Forest Fire model – Justification n Communities: n Newcomer copies neighbors’ links n Shrinking diameter 44

School of Computer Science Carnegie Mellon Conclusion (1) n We study evolution of graphs over time n We discover: n Densification Power Law n Shrinking Diameters n Propose explanation: n Community Guided Attachment leads to Densification Power Law 45

School of Computer Science Carnegie Mellon Conclusion (2) n Proposed Forest Fire Model uses only 2 parameters to generate realistic graphs: Heavy-tailed in- and out-degrees Densification Power Law Shrinking diameter 46

School of Computer Science Carnegie Mellon Thank you! Questions? jure@cs. cmu. edu 47

School of Computer Science Carnegie Mellon Dynamic Community Guided Attachment n The community tree grows n At each iteration a new level of nodes gets added n New nodes create links among themselves as well as to the existing nodes in the hierarchy n Based on the value of parameter c we get: a) Densification with heavy-tailed in-degrees b) Constant average degree and heavy-tailed in-degrees c) Constant in- and out-degrees n But: n Community Guided Attachment still does not obey the shrinking diameter property 48

School of Computer Science Carnegie Mellon Densification Power Law (1) n Theorem: Community Guided Attachment random graph model, the expected out-degree of a node is proportional to 49

School of Computer Science Carnegie Mellon Forest Fire – the Model n 2 parameters: n p … forward burning probability n r … backward burning ratio n Nodes arrive one at a time n New node v attaches to a random node – the ambassador n Then v begins burning ambassador’s neighbors: n Burn X links, where X is binomially distributed n Choose in-links with probability r times less than out- links n Fire spreads recursively n Node v attaches to all nodes that got burned 50

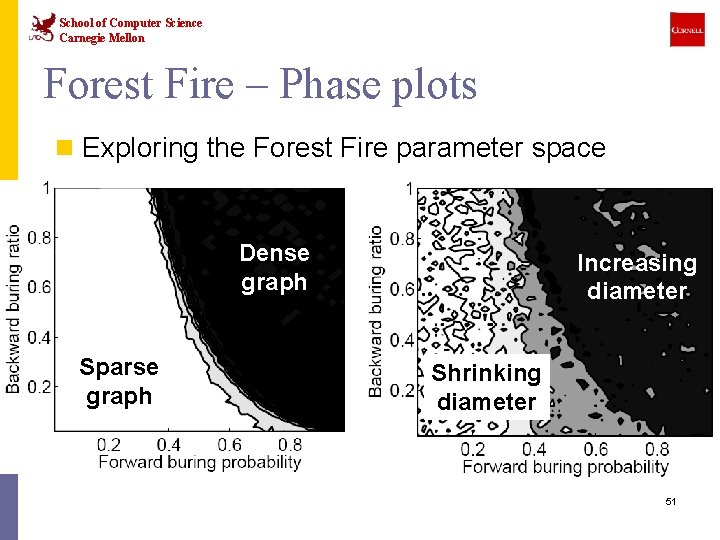
School of Computer Science Carnegie Mellon Forest Fire – Phase plots n Exploring the Forest Fire parameter space Dense graph Sparse graph Increasing diameter Shrinking diameter 51

School of Computer Science Carnegie Mellon Forest Fire – Extensions n Orphans: isolated nodes that eventually get connected into the network n Example: citation networks n Orphans can be created in two ways: n start the Forest Fire model with a group of nodes n new node can create no links n Diameter decreases even faster n Multiple ambassadors: n Example: following paper citations from different fields n Faster decrease of diameter 52

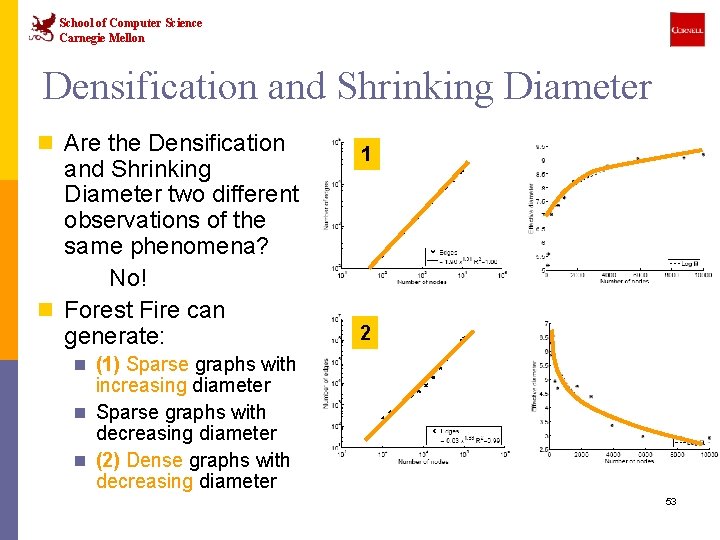
School of Computer Science Carnegie Mellon Densification and Shrinking Diameter n Are the Densification and Shrinking Diameter two different observations of the same phenomena? No! n Forest Fire can generate: 1 2 n (1) Sparse graphs with increasing diameter n Sparse graphs with decreasing diameter n (2) Dense graphs with decreasing diameter 53