Graphs of Trigonometric Functions Graph of the Sine

Graphs of Trigonometric Functions

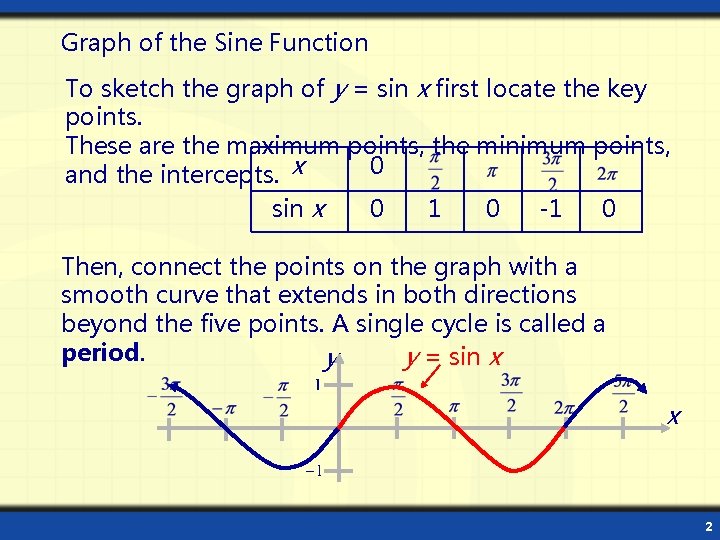
Graph of the Sine Function To sketch the graph of y = sin x first locate the key points. These are the maximum points, the minimum points, 0 and the intercepts. x sin x 0 1 0 -1 0 Then, connect the points on the graph with a smooth curve that extends in both directions beyond the five points. A single cycle is called a period. y = sin x y x 2

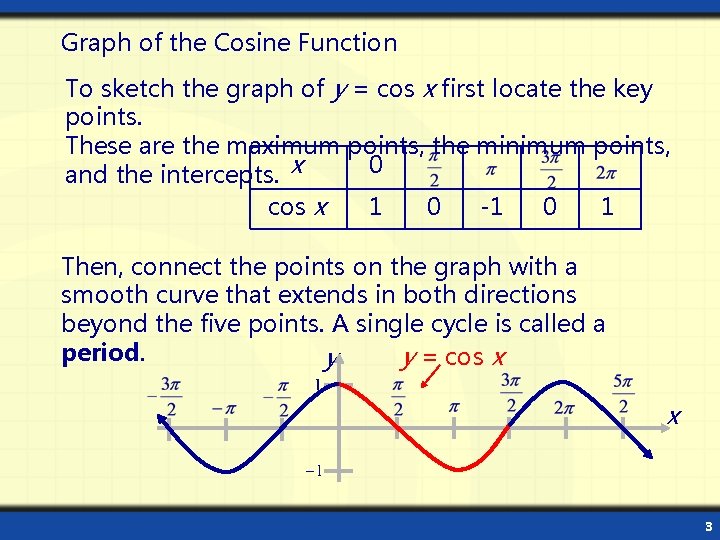
Graph of the Cosine Function To sketch the graph of y = cos x first locate the key points. These are the maximum points, the minimum points, 0 and the intercepts. x cos x 1 0 -1 0 1 Then, connect the points on the graph with a smooth curve that extends in both directions beyond the five points. A single cycle is called a period. y = cos x y x 3

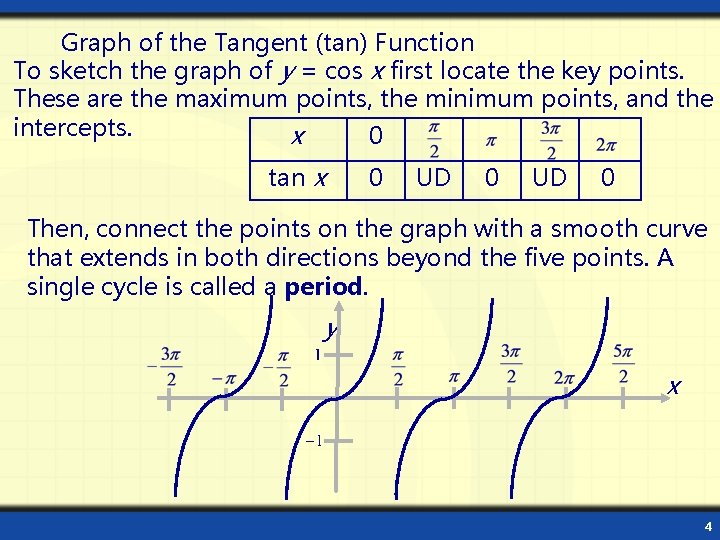
Graph of the Tangent (tan) Function To sketch the graph of y = cos x first locate the key points. These are the maximum points, the minimum points, and the intercepts. x 0 tan x 0 UD 0 Then, connect the points on the graph with a smooth curve that extends in both directions beyond the five points. A single cycle is called a period. y x 4

Properties of Sine and Cosine Functions The graphs of y = sin x and y = cos x have similar properties: 1. The domain is the set of real numbers. 2. The range is the set of y values such that . 3. The maximum value is 1 and the minimum value is – 1. 4. The graph is a smooth curve. 5. Each function cycles through all the values of the range over an x-interval of. 6. The cycle repeats itself indefinitely in both directions of the x-axis. 5

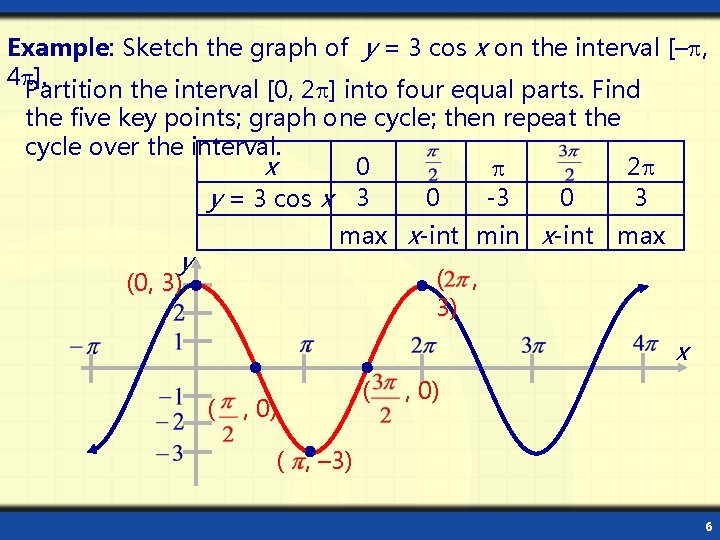
Example: Sketch the graph of y = 3 cos x on the interval [– , 4 ]. Partition the interval [0, 2 ] into four equal parts. Find the five key points; graph one cycle; then repeat the cycle over the interval. x 0 2 0 -3 0 3 y = 3 cos x 3 max x-int min x-int max y ( , 3) (0, 3) x ( , 0) ( , – 3) 6

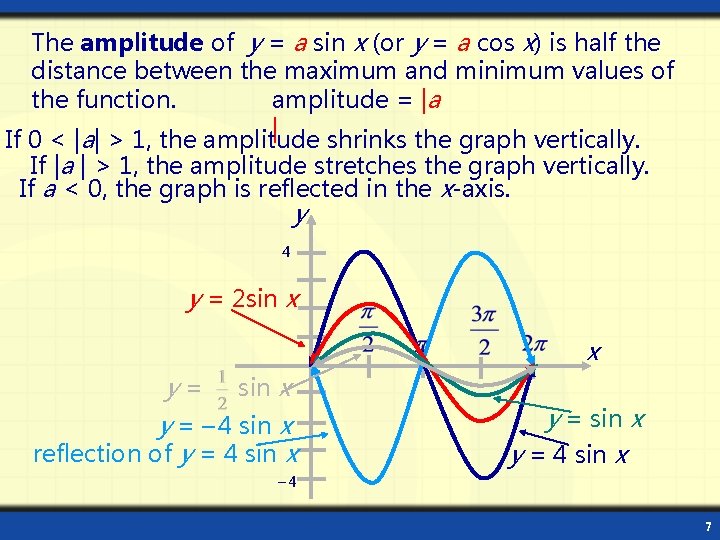
The amplitude of y = a sin x (or y = a cos x) is half the distance between the maximum and minimum values of amplitude = |a the function. | If 0 < |a| > 1, the amplitude shrinks the graph vertically. If |a | > 1, the amplitude stretches the graph vertically. If a < 0, the graph is reflected in the x-axis. y y = 2 sin x x y = sin x y = – 4 sin x reflection of y = 4 sin x 7

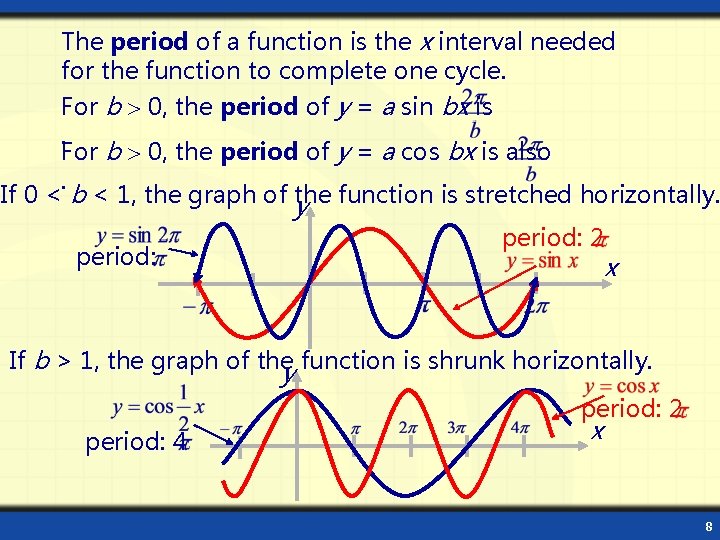
The period of a function is the x interval needed for the function to complete one cycle. For b 0, the period of y = a sin bx is. For b 0, the period of y = a cos bx is also. If 0 < b < 1, the graph of the function is stretched horizontally. y period: 2 x If b > 1, the graph of the function is shrunk horizontally. y period: 2 period: 4 x 8

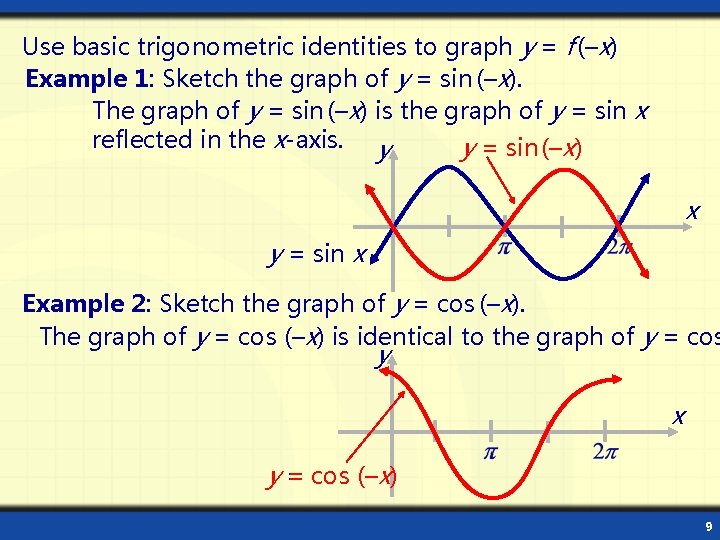
Use basic trigonometric identities to graph y = f (–x) Example 1: Sketch the graph of y = sin (–x). The graph of y = sin (–x) is the graph of y = sin x reflected in the x-axis. y y = sin (–x) x y = sin x Example 2: Sketch the graph of y = cos (–x). The graph of y = cos (–x) is identical to the graph of y = cos y x y = cos (–x) 9

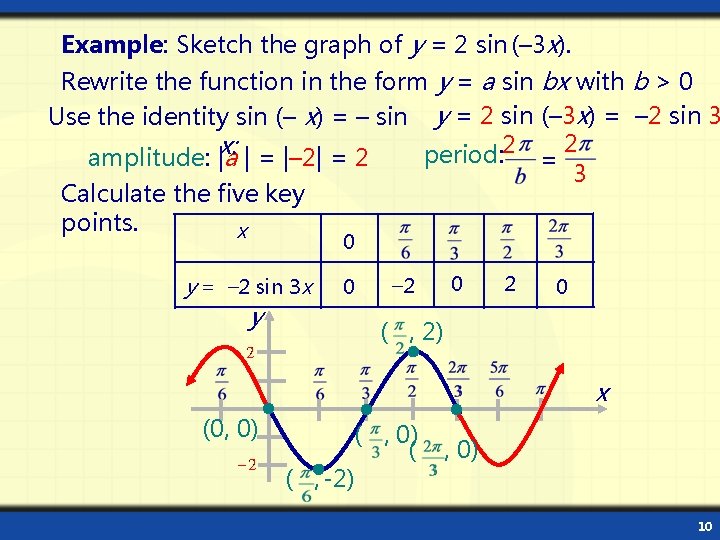
Example: Sketch the graph of y = 2 sin (– 3 x). Rewrite the function in the form y = a sin bx with b > 0 Use the identity sin (– x) = – sin y = 2 sin (– 3 x) = – 2 sin 3 x: period: 2 = 2 amplitude: |a | = |– 2| = 2 3 Calculate the five key points. x 0 y = – 2 sin 3 x y 0 – 2 0 ( , 2) x (0, 0) ( ( , -2) , 0) 10

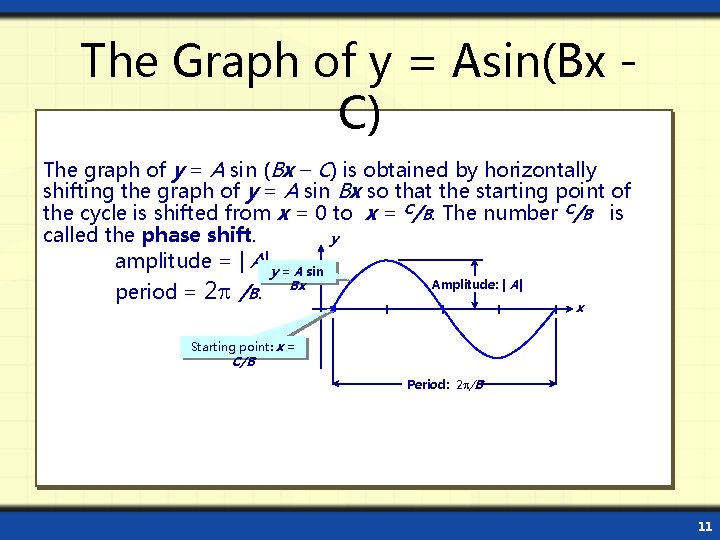
The Graph of y = Asin(Bx C) The graph of y = A sin (Bx – C) is obtained by horizontally shifting the graph of y = A sin Bx so that the starting point of the cycle is shifted from x = 0 to x = C/B. The number C/B is called the phase shift. y amplitude = | A| y = A sin period = 2 /B. Bx Amplitude: | A| x Starting point: x = C/B Period: 2 /B 11

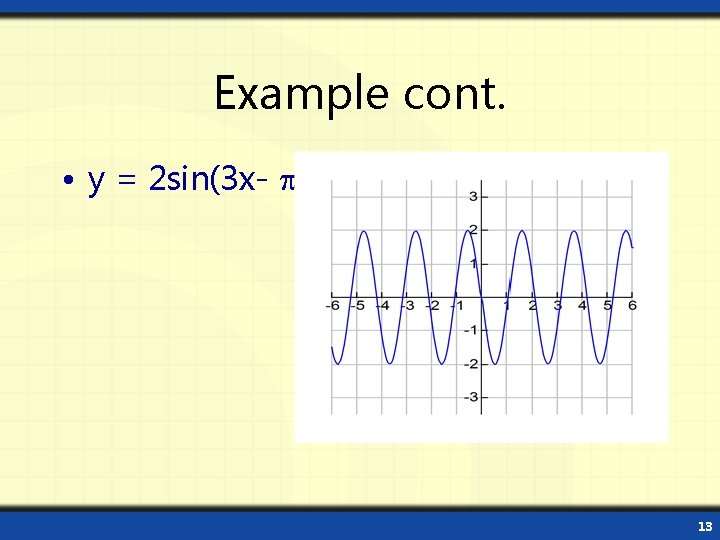
Example Determine the amplitude, period, and phase shift of y = 2 sin(3 x- ) Solution: Amplitude = |A| = 2 period = 2 /B = 2 /3 phase shift = C/B = /3 12

Example cont. • y = 2 sin(3 x- ) 13

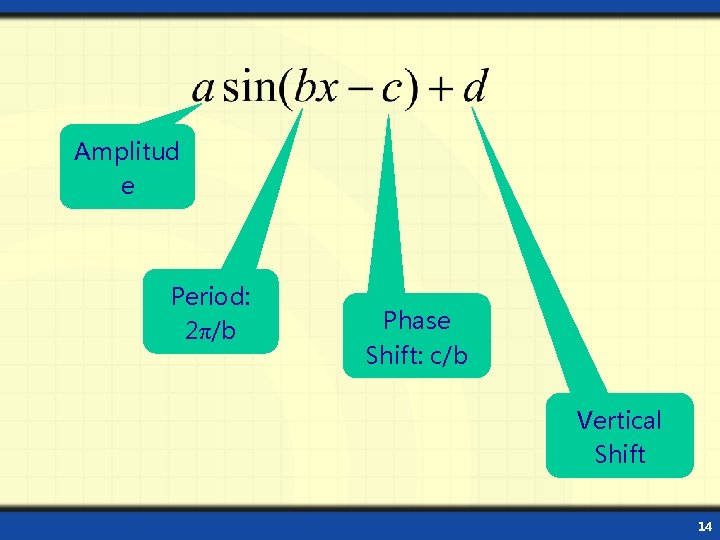
Amplitud e Period: 2π/b Phase Shift: c/b Vertical Shift 14