Graphs of Quadratic Equations Standard Form y ax

Graphs of Quadratic Equations

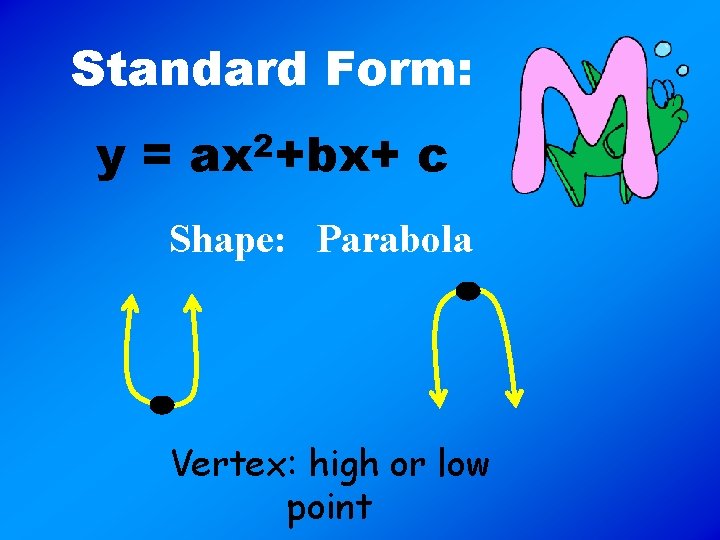
Standard Form: y = ax 2+bx+ c Shape: Parabola Vertex: high or low point

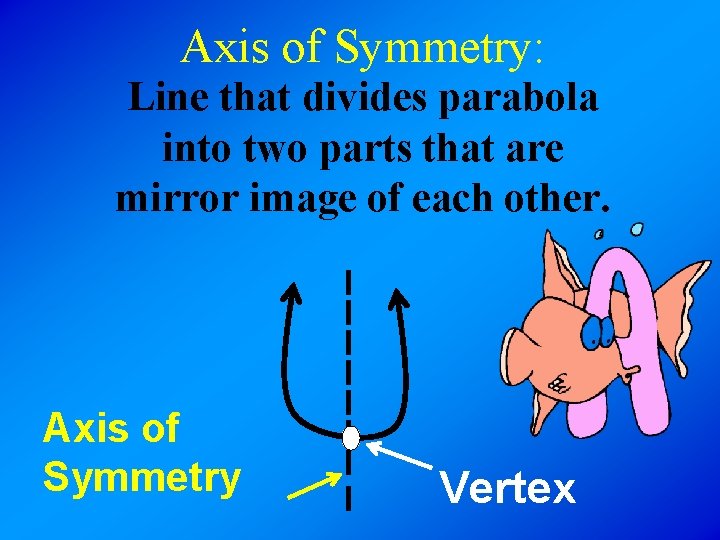
Axis of Symmetry: Line that divides parabola into two parts that are mirror image of each other. Axis of Symmetry Vertex

The vertex has an x-coordinate of The axis of symmetry is the vertical line passing through

y= 2 x First find the vertex. 0 is the axis of symmetry: This is the x value of the vertex, now find the y value. If x = 0, y = 0 Vertex = (0, 0)

Example: y = 2 x Make a table for y = 2 x Since the vertex is (0, 0), pick an x value to the right and left of 0.

To graph a Quadratic Equation 2 2 y = ax +bx+c y = -ax +bx+c If a is positive, the parabola opens up If a is negative, the parabola opens down

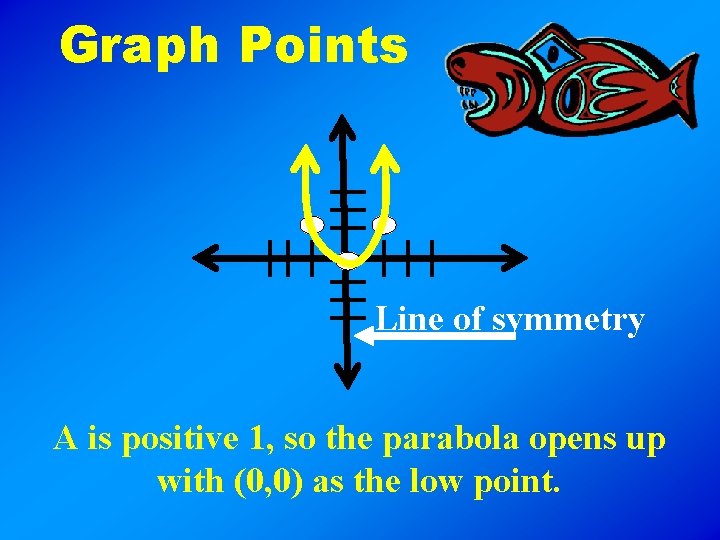
Graph Points Line of symmetry A is positive 1, so the parabola opens up with (0, 0) as the low point.

GRAPH: y = 2 x -x-6 • Identify the a, b, and c values • First find the vertex • Make a table with an x value to the right and left of the vertex x value • Graph these points and connect. • Label the vertex

Find vertex and plug in to find y. value to have high or low point. 1.

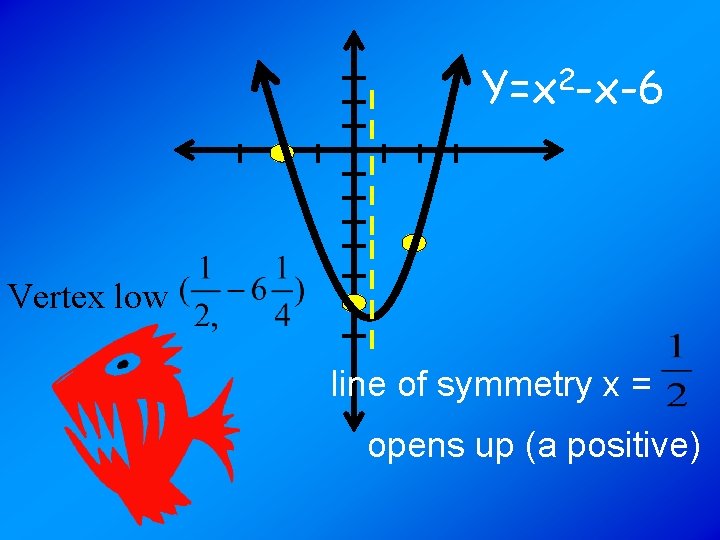
The x value of the vertex is 1/2 • Now find the y value of the vertex by plugging x back into the equation. y = x 2 -x-6 • y = (1/2)2 – ½ - 6 • The y value is -25/4. • Now pick a point to the left and right of ½.

GRAPH: y = 2 x -x-6 I try to pick points equal distance from the vertex x value. I also tried 0 here.

Y=x 2 -x-6 Vertex low line of symmetry x = opens up (a positive)

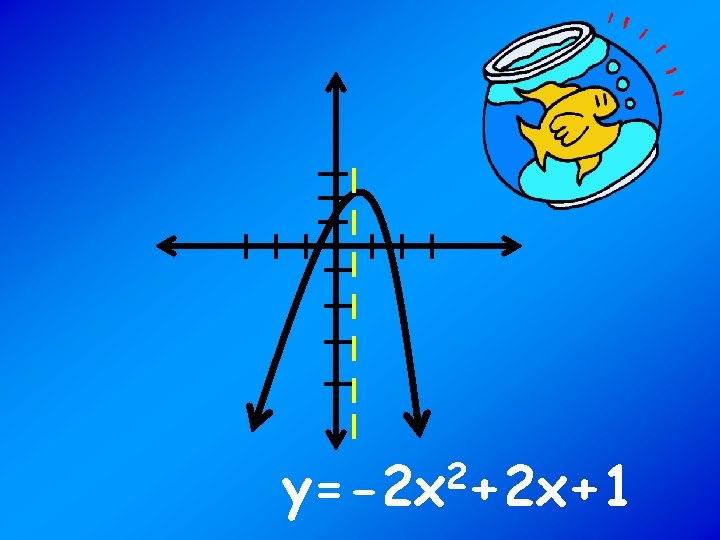
Graph: y= 2 -2 x +2 x+1 a is negativeopens down Line of Symmetry Find the y value, then pick a point to the left and right of 1/2 to see how to draw the parabola. =1 2

2 y=-2 x +2 x+1

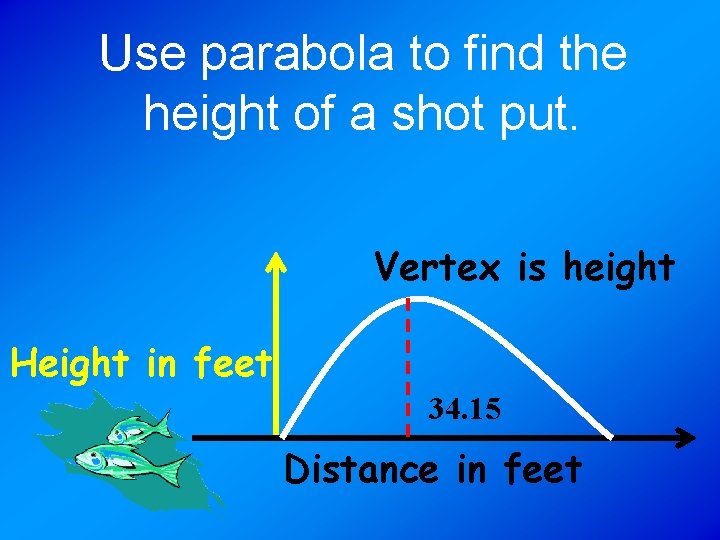
Use parabola to find the height of a shot put. Vertex is height Height in feet 34. 15 Distance in feet

Equation: y= USE CALCULATO R! 2 -. 01464 x +x+5

Put x back in to find y value y= 2 -. 01464(34. 15) +34. 15+5 = 22. 08 ft. high (34. 15, 22. 08) vertex (high point)