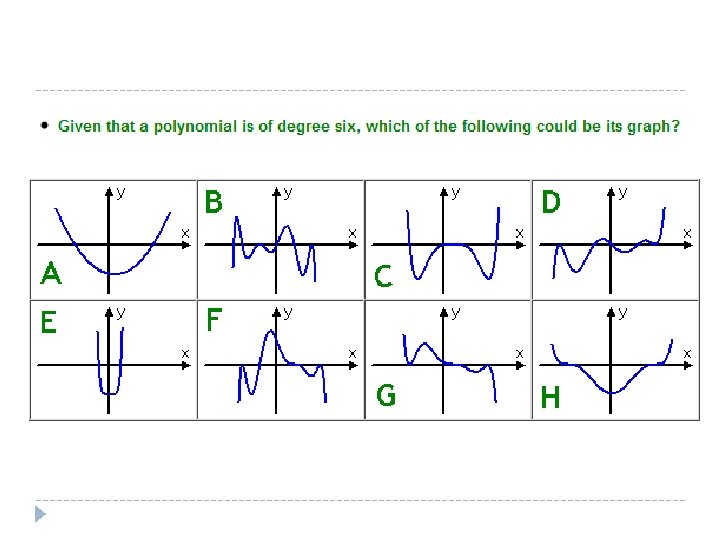
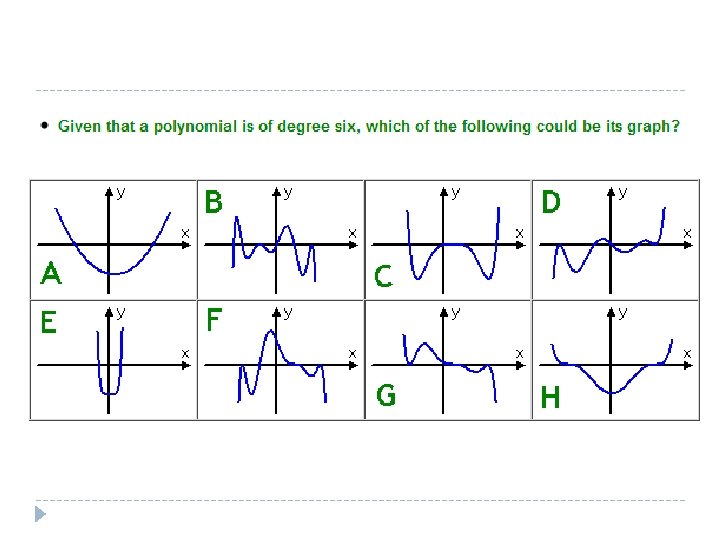
Graphs of Polynomial Functions E Q What can






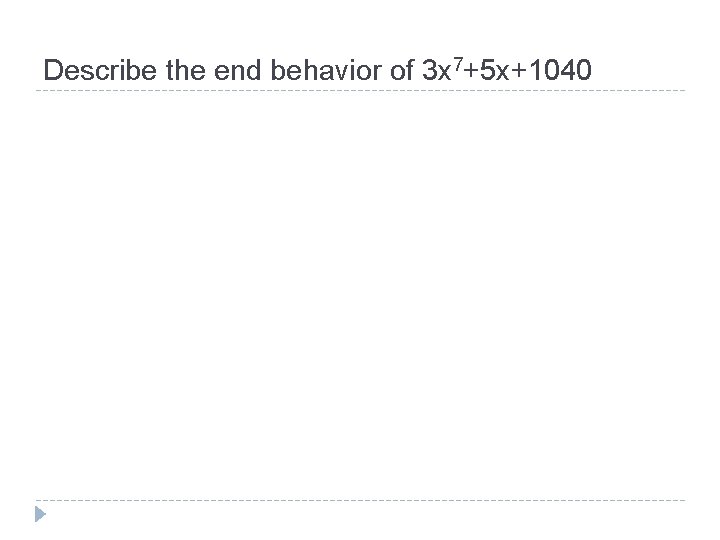








- Slides: 28

Graphs of Polynomial Functions E. Q: What can we learn about a polynomial from its graph?

Basic Polynomial Shapes � Basic form axn where a is a constant and n is a nonnegative integer � Odd polynomials- highest exponent is odd (3, 5, 7) � Even polynomials- highest exponent is even (2, 4, 6) � Odd and even polynomials have similarities in their shapes

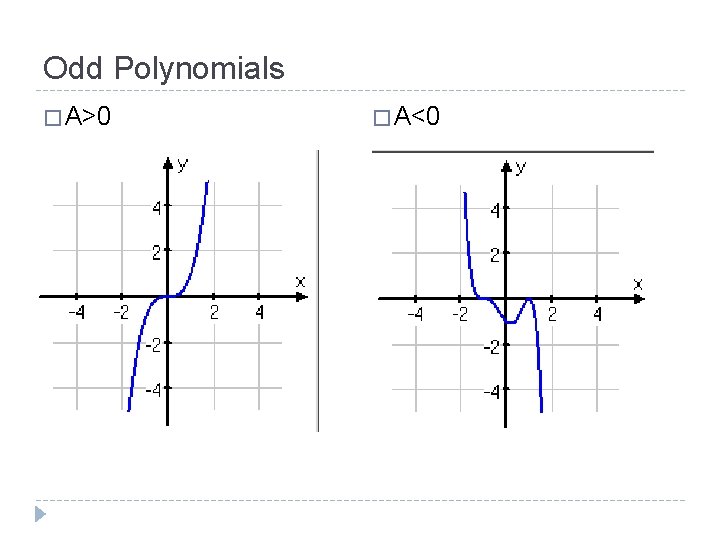
Odd Polynomials � A>0 � A<0

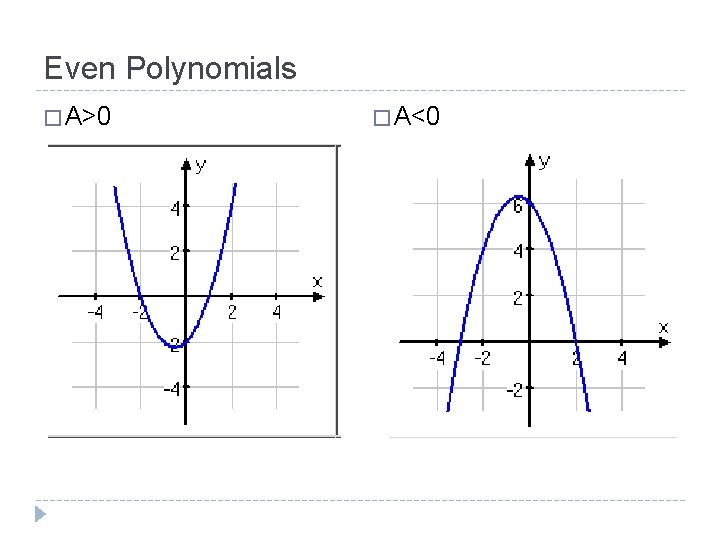
Even Polynomials � A>0 � A<0

Continuity � Every graph of a polynomial is continuous � Unbroken curve � No jumps � No sharp corners

End Behavior � Consider the function f(x)=2 x 3+x 2 -6 x and the function determined by its leading coefficient g(x)=2 x 3 � Hit zoom 6 on the calculator � Graph f and g. � Record their differences and similarities on a sheet of paper in your group � Change the window to -20<x<20 and 10, 000<y<10, 000 and graph f and g � Do the windows look almost the same? Describe any changes on your sheet of paper

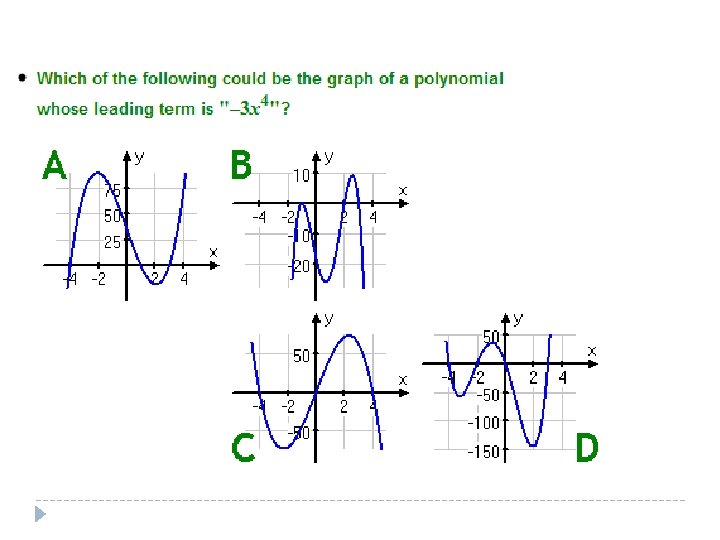
End Behavior � Looks at the shape of a polynomial graph at the far left and far right of the graph � Common characteristics exist between odd and even degree polynomials � When a polynomial function has an odd degree, one end of the graph shoots upward and one end shoots downward � When a polynomial function has an even degree, both ends of the graph shoot upward or downward

End Behavior � The end behavior of the graph of the polynomial is the same as the end behavior of the graph of the leading term or highest exponent.

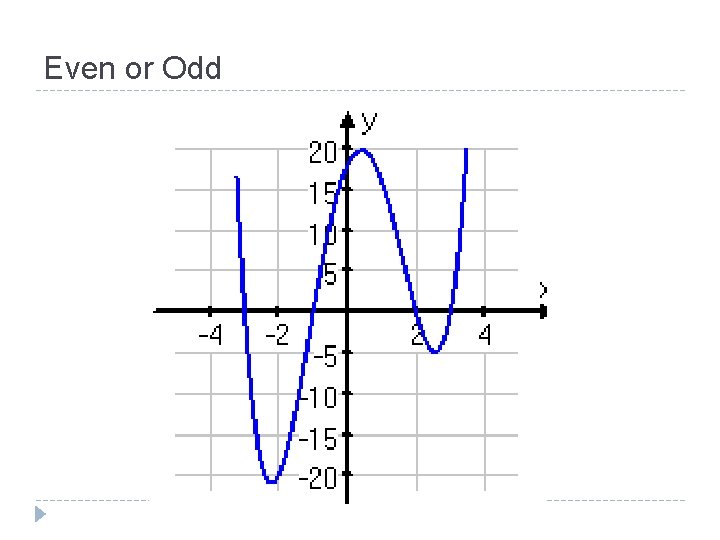
Even or Odd

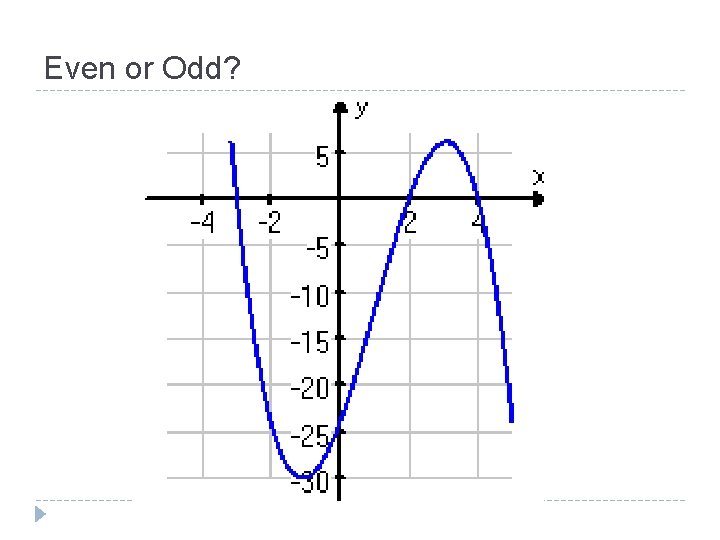
Even or Odd?

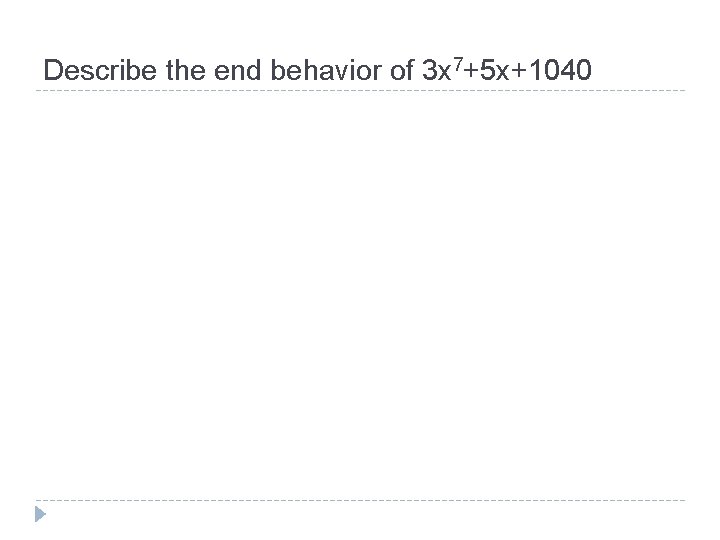
Describe the end behavior of 3 x 7+5 x+1040

Intercepts � For any polynomial function �Y intercept is the constant term in the equation � X intercepts are the real zeros of the polynomial Found using synthetic division or zero finder on calculator May need to use both synthetic division and the zero finder to completely factor real solutions � � A polynomial will always have one y intercept Will have n real zeros where n is the value of the highest exponent

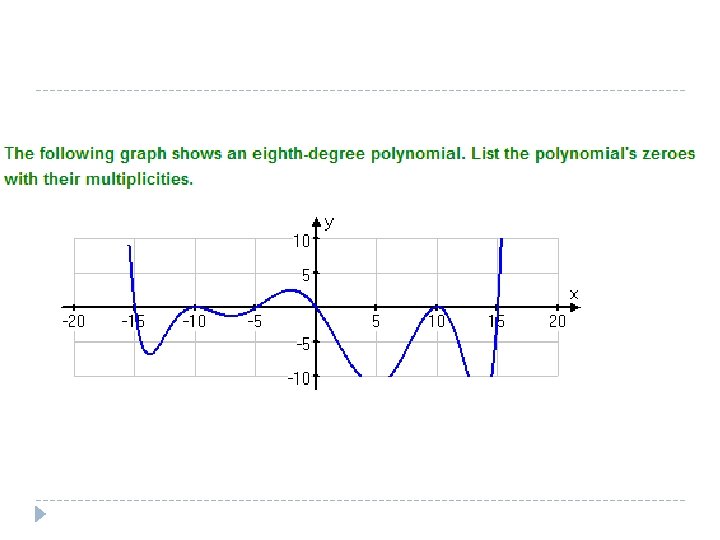
Multiplicity � Sometimes polynomials have repeating factors � Consider 2 x 5 -10 x 4+7 x 3+13 x 2+3 x+9 � Linear factors are (x+1)(x-3)(2 x 2+1) � The (x-3) is a factor twice � This is called multiplicity � Can write the factors as (x+1)(x-3)2(2 x 2+1)

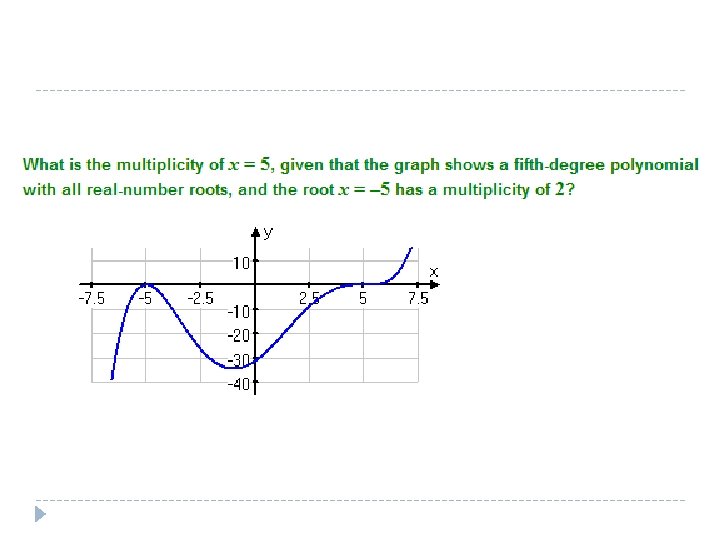
Multiplicity � If x-r is a factor of the polynomial that occurs more than once we say it has multiplicity. � General rules govern the idea of multiplicity � If the multiplicity occurs as an odd number � The � If graph crosses the x axis at c the multiplicity occurs as an even number � The graph does not cross the axis, it only touches the axis

Will the multiplicity cause the graph to cross or touch the x axis? � F(x)=(x+1)2(x-2)(x-3)3




Local Extrema and Points of Inflection


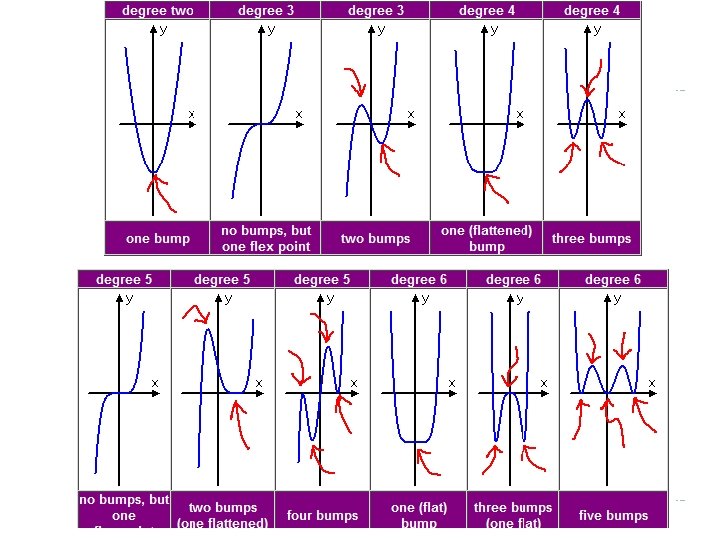
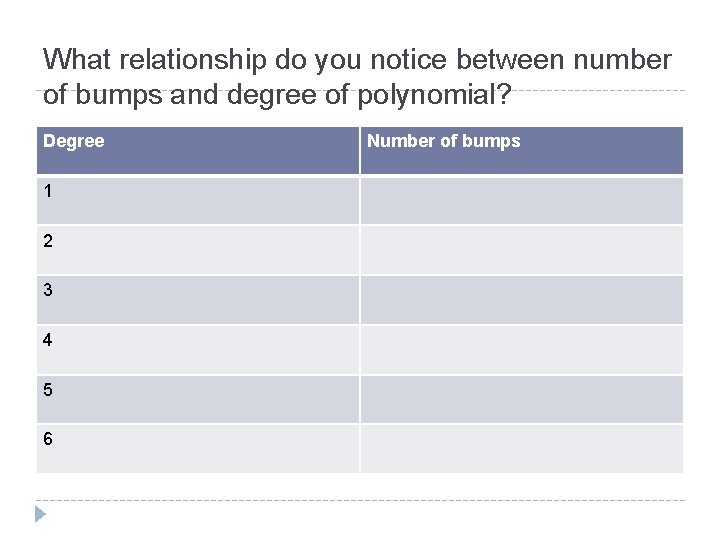
What relationship do you notice between number of bumps and degree of polynomial? Degree 1 2 3 4 5 6 Number of bumps

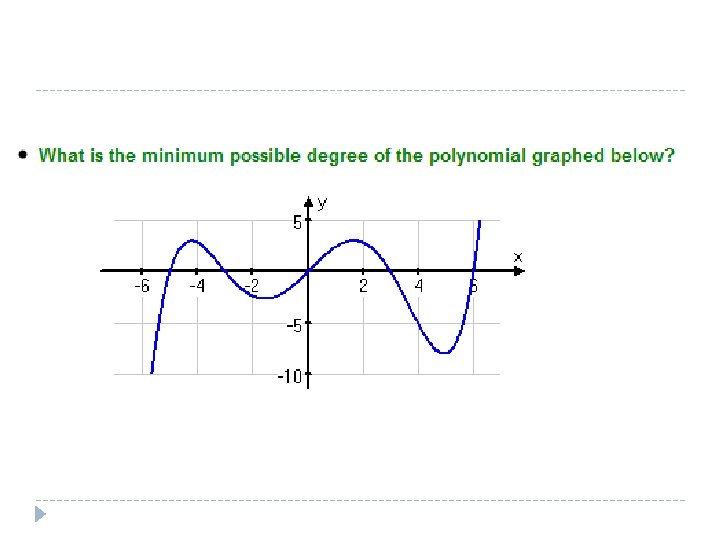
The relationship � For a polynomial of degree n, there at most n-1 “bumps” � Formally known as local extrema � Local extrema- either a local minimum or maximum point � Where the graph has a peak or a valley � Here the output changes from increasing to decreasing or vice versa

Points of Inflection � Inflection points occur where you have local extrema. � Here the concavity of the graph changes � The graph of a polynomial of degree n with n greater than or equal to 2 has at most n-2 points of inflection � The graph of an odd degree polynomial with n>2 has at least one point of inflection



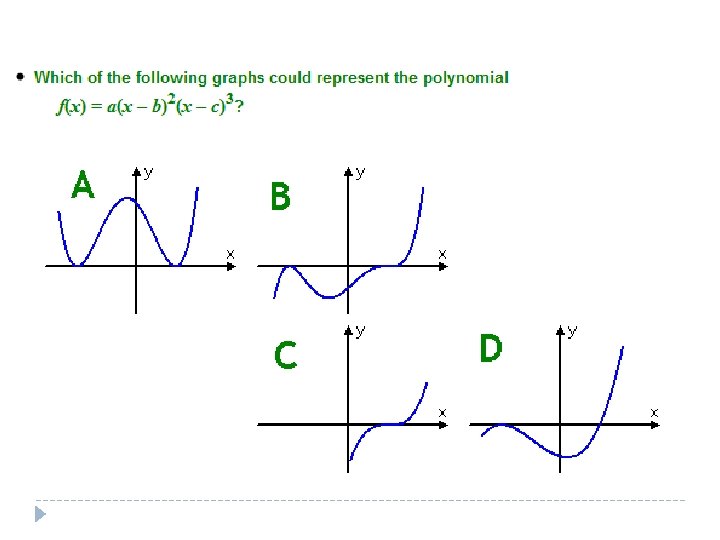
Choosing the answer � First rule out the choices with too many bumps (peaks and valleys) � What is the maximum number of bumps I can have? � Think about end behavior- which way should this go, one up, one down, or both ends in the same direction? � Look at multiplicity- which may add up to a sixth degree polynomial?
