GRAPHS OF POLAR EQUATIONS DR SHILDNECK POINT PLOTTING

GRAPHS OF POLAR EQUATIONS DR. SHILDNECK

POINT PLOTTING One way of graphing a polar equation, like most others, is point plotting. • First, make a table of values that satisfy the equation. – Remember that in general, r depends on Ѳ. – Make a table (like an x/y table) using Ѳ (instead of x) and r (instead of y). – Choose (wisely) values for Ѳ. – Plug those values into the equation and get the corresponding values for r. • Second, plot those points. • Third, connect the points (in order) with a smooth curve. – Note, it is easy to not get the correct graph. Make sure that you connect the points IN ORDER. – You might want to “connect the dots” every 2 -3 points rather than waiting until the end.

POINT PLOTTING [Example 1] Graph. r = 4 cos Ѳ Ѳ 0 30 45 60 90 r 4 3. 5 2. 8 2 0 120 135 150 180 210 225 240 270 300 315 330 360 -2 -2. 8 -3. 5 -4 -3. 5 -2. 8 -2 0 2 2. 8 3. 5 4

SYMMETRY AND IMPLICATIONS Another way of graphing polar equations is to test for symmetry and limit the number of points you must plot. • First, test for symmetry. If a specific symmetry exists, you can complete ½ of a table and translate those points through reflection. • Second, make an appropriate table. • Third, plot points. • Finally, connect the points (in order) with a smooth curve.

TESTING FOR SYMMETRY Use the equation you want to graph and replace the appropriate variables. Compare the simplified result with the original to determine which symmetry exists. Note, that if an equation fails a symmetry test, it might still exhibit that symmetry. 1. Replace Ѳ with – Ѳ. If the equation is equal to the original, then the graph is symmetric with respect to the polar axis (x-axis). – Make a table from 0 to pi. 2. Replace (r, Ѳ) with (-r, - Ѳ). If the equation is equivalent, then the graph is symmetric with respect to the line Ѳ = pi/2 (y-axis) – Make a table from –pi to pi. 3. Replace r with –r. If the equation is equal to the original, then the graph is symmetric with respect to the pole (origin) – Make a table for the first quadrant and either the 2 nd or 4 th.

TESTING FOR SYMMETRY [Example 2] Determine a symmetry that each graph exhibits. A) r = 4 cosѲ A) Plug in (- Ѳ). r = 4 cos(-Ѳ) = 4 cos(Ѳ) Yes… w/rpt x-axis. B) Plug in (- Ѳ). B) r = 1 – cosѲ r = 1 - cos(-Ѳ) = 1 - cos(Ѳ) Yes… w/rpt x-axis. C) r = 1 + 2 sinѲ C) Plug in (-Ѳ), then –r, then both. None of them come up the same as the original equation. No Symmetry. D) r = 3 sin(5Ѳ) E) D) Plug in (-r). (-r, -Ѳ). (-r)=2 3 sin(-5Ѳ) -r = 4 sin(2Ѳ) -r = -3 sin(5Ѳ) (-r) = 4 sin(2Ѳ) 2 2 E) r = 4 sin(2Ѳ) r ==3 sin(5Ѳ) 4 sin(2Ѳ) Yes… w/rpt Pole. y-axis.

GRAPHING WITH SYMMETRY [Example 3] Graph. r = 1 + 2 sinѲ Ѳ 0 30 45 60 90 120 135 150 180 r 1 2 2. 4 2. 7 3 2. 7 Ѳ r 2. 4 2 210 225 240 270 300 315 330 360 0 -. 4 -. 7 -1 -. 7 -. 4 0 1 1

SPECIAL POLAR GRAPHS There are several special polar curves that you should be able to recognize both by picture and equation. We have talked about some of these already. They include: 1. r = c, where c is a real number 2. r = Ѳ 3. Ѳ = c, where c is a real number The more complex polar curves that you should know are detailed in the pages that follow.

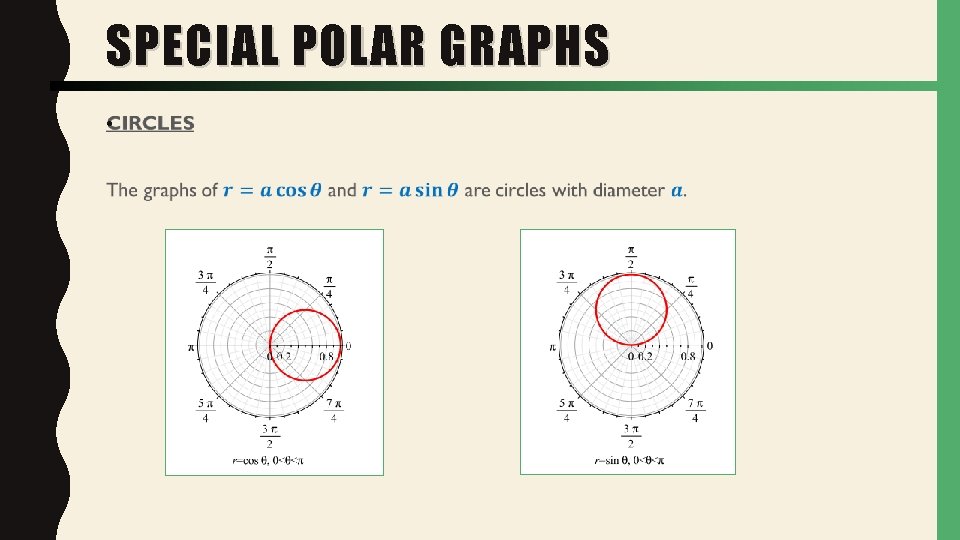
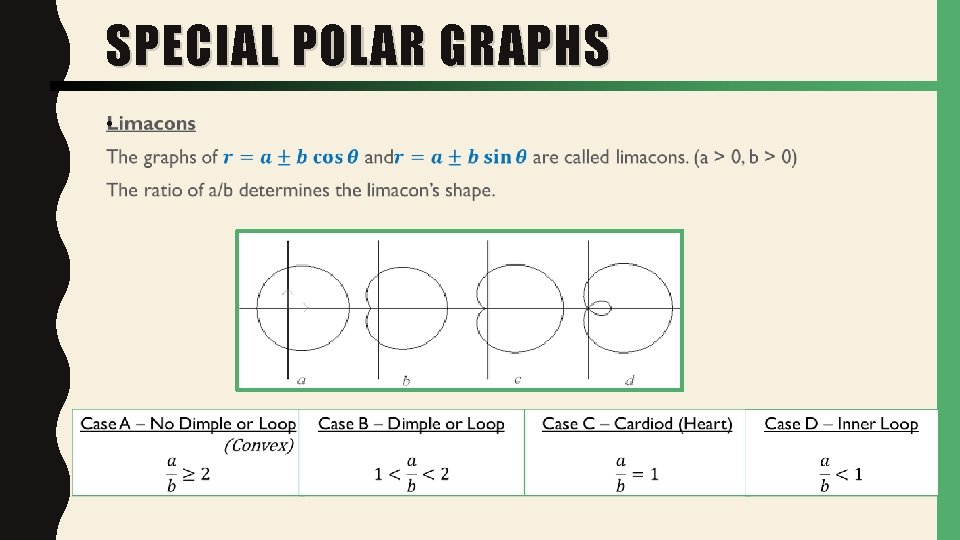
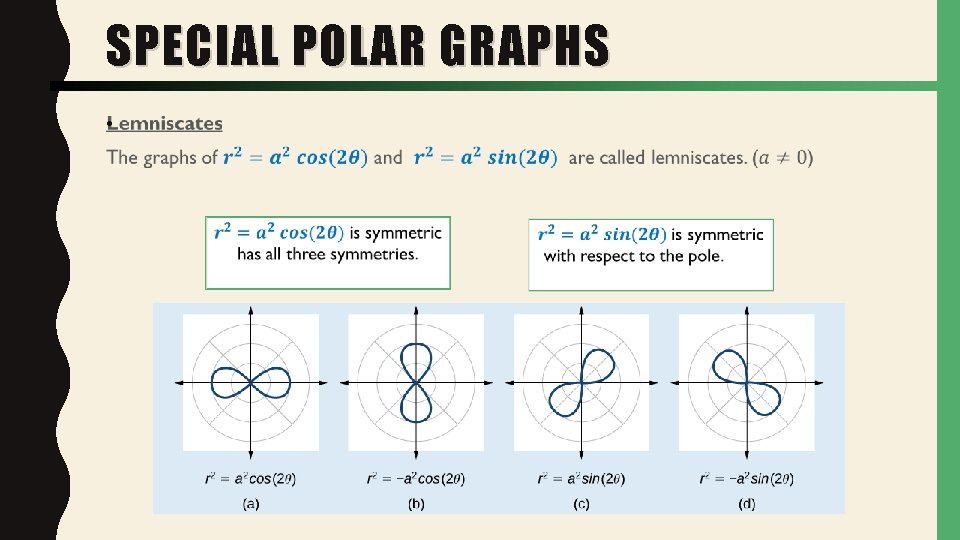
SPECIAL POLAR GRAPHS •

SPECIAL POLAR GRAPHS •

SPECIAL POLAR GRAPHS •

SPECIAL POLAR GRAPHS •

EXPECTATIONS FOR GRAPHS You should be able to: 1. Recognize the equations and pictures of special curves. 2. NAME special curves given their equation or picture. 3. Determine the symmetries that help you graph polar curves. 4. Create an appropriate table for plotting points of special curves. 5. Graph polar curves.

ASSIGNMENT Alternate Text (posted on Blog) P. 720 – 721 #1 -18 all #23, 24, 25, 27, 29, 33, 35 (by hand) #37 -51 odd (in calculator) #59 -62 all (in calculator) Graph Paper will be posted on the blog.