Graphs of Functions Skill 03 Objectives Find the

Graphs of Functions Skill 03

Objectives… • Find the domains and ranges of functions and use the Vertical Line Test for functions • Determine intervals on which functions are increasing, decreasing, or constant • Determine relative maximum and relative minimum values of functions • Identify and graph step functions and other piecewise-defined functions • Identify even and odd functions

The Graph of a Function The graph of a function f is the collection of ordered pairs (x, f (x)), such that x is in the domain of f. x = the distance from the y-axis y = f (x) = the distance from the x-axis

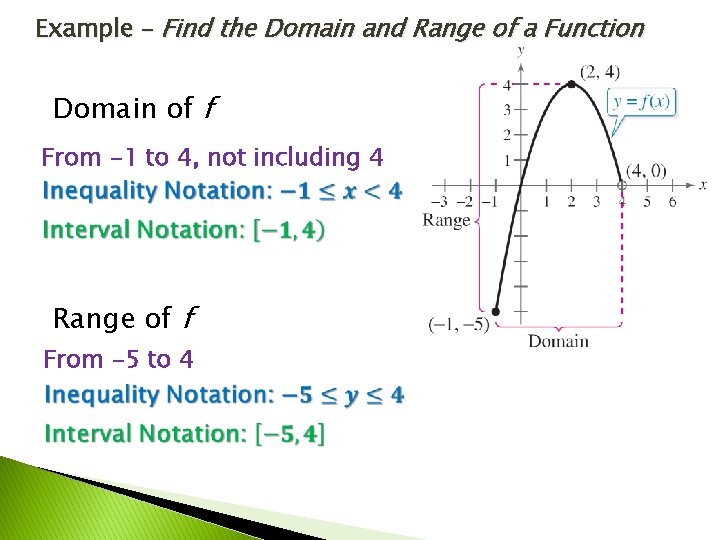
Example – Find the Domain and Range of a Function Domain of f From -1 to 4, not including 4 Range of f From -5 to 4

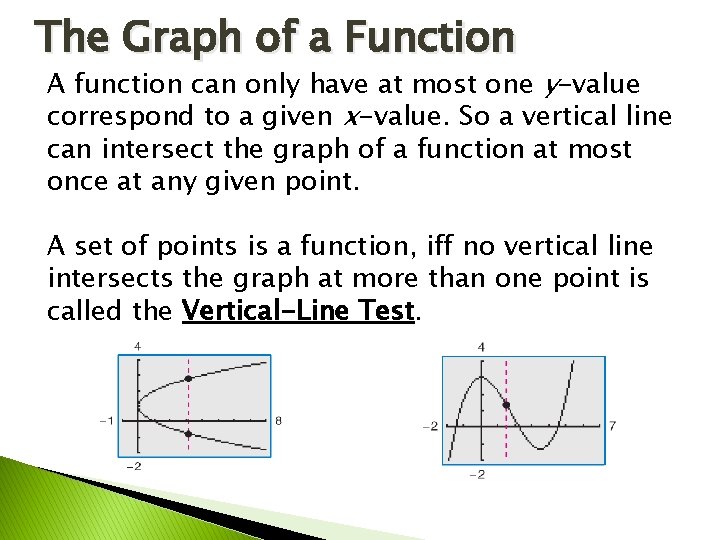
The Graph of a Function A function can only have at most one y-value correspond to a given x-value. So a vertical line can intersect the graph of a function at most once at any given point. A set of points is a function, iff no vertical line intersects the graph at more than one point is called the Vertical-Line Test.

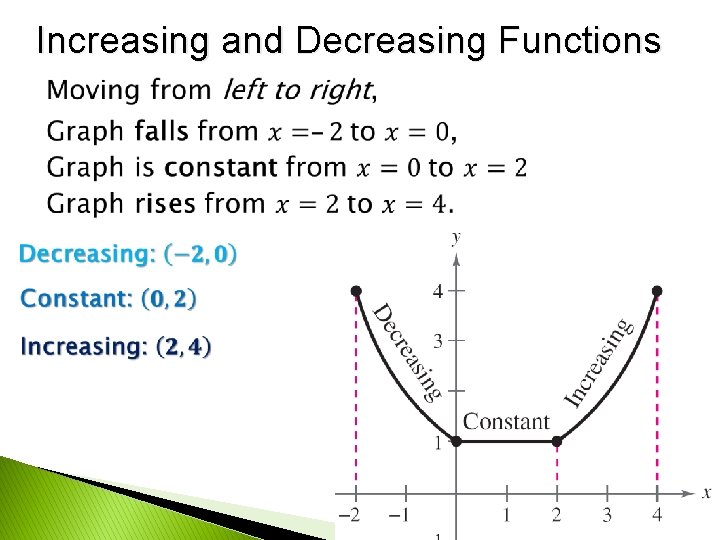
Increasing and Decreasing Functions

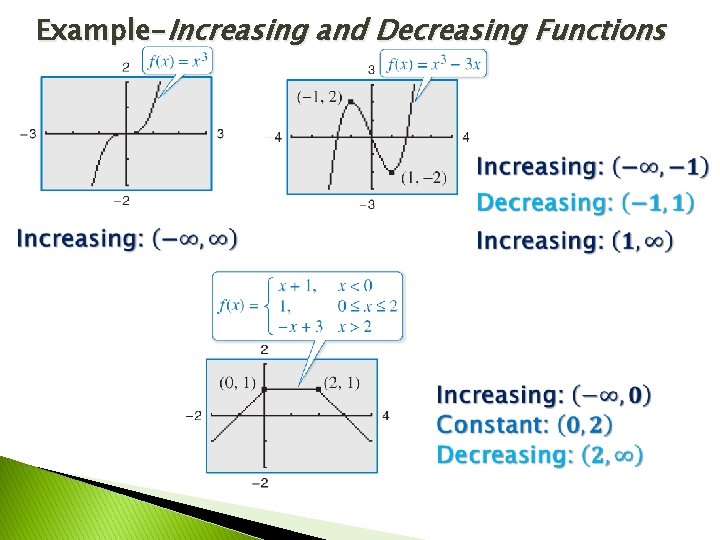
Example-Increasing and Decreasing Functions

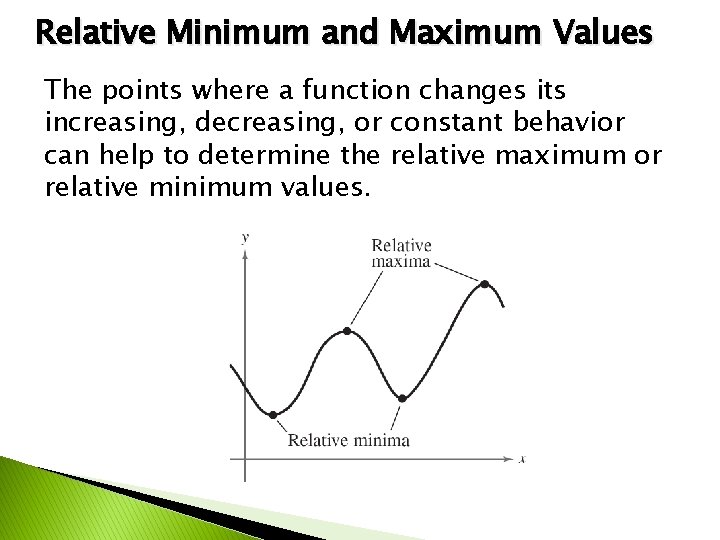
Relative Minimum and Maximum Values The points where a function changes its increasing, decreasing, or constant behavior can help to determine the relative maximum or relative minimum values.

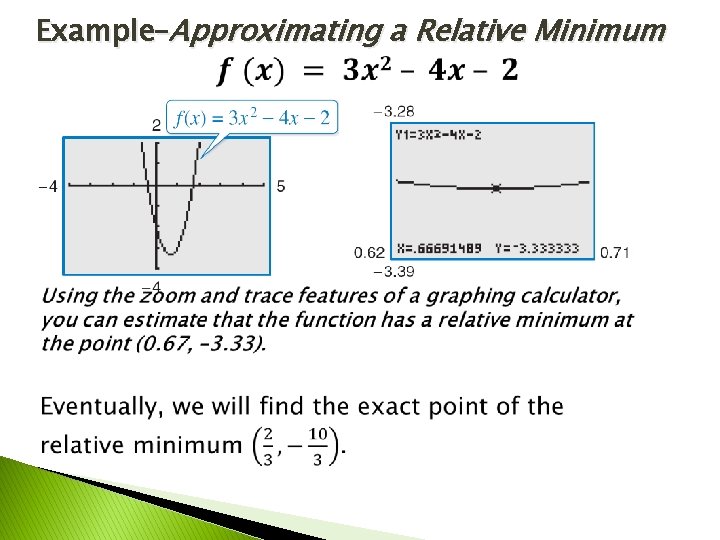
Example–Approximating a Relative Minimum

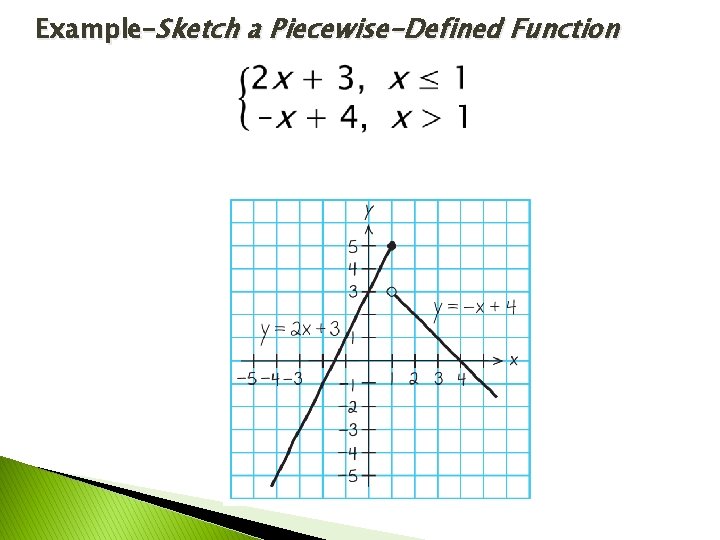
Example–Sketch a Piecewise-Defined Function

Even and Odd Functions A graph has symmetry with respect to the y-axis if (x, y) and (–x, y) is on the graph. This is an even function.

Even and Odd Functions A graph has symmetry with respect to the origin if (x, y) and (–x, –y) is on the graph. This is an odd function.

Even and Odd Functions A graph has symmetry with respect to the x-axis if (x, y) and (x, –y) is on the graph. This is neither even nor odd. It is not a function.

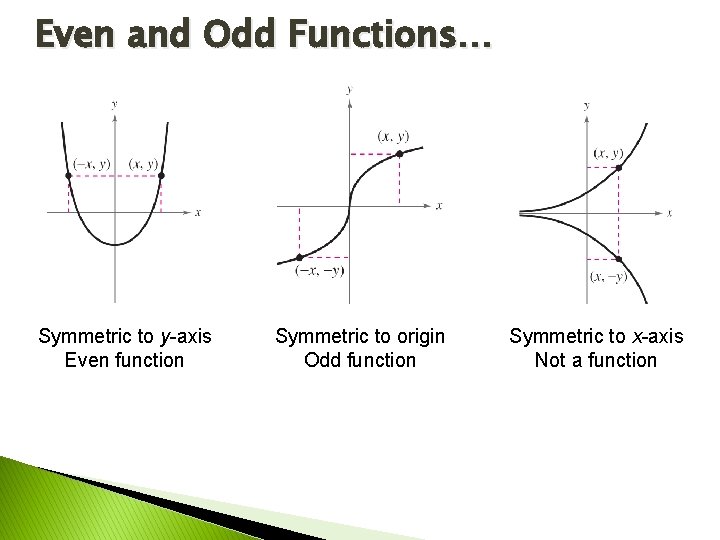
Even and Odd Functions… Symmetric to y-axis Even function Symmetric to origin Odd function Symmetric to x-axis Not a function

Example–Even and Odd Functions Is each function even, odd, or neither.

Skill 3; Graphs of Functions � Summarize � Questions? � Homework ◦ Worksheet Notes