Graphs II Graphs A graph is a set

Graphs II

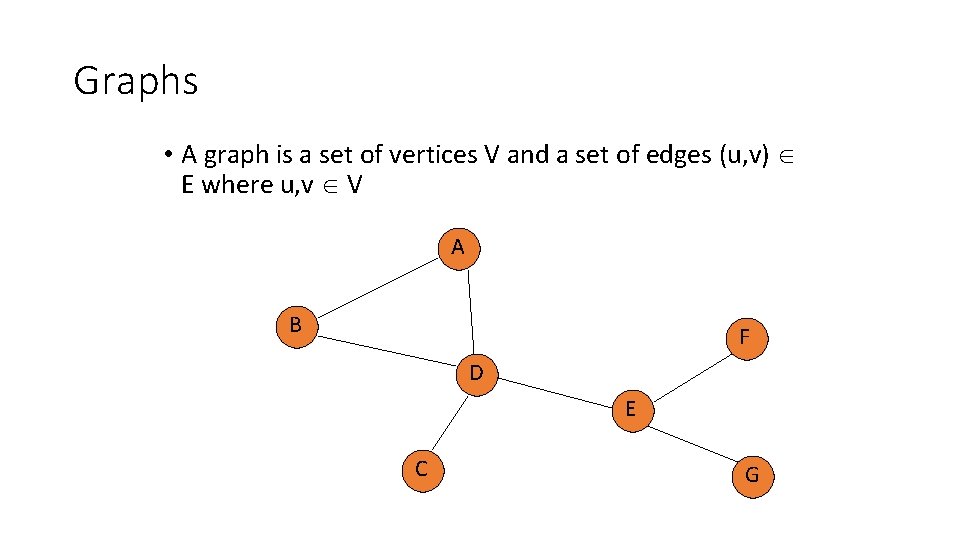
Graphs • A graph is a set of vertices V and a set of edges (u, v) E where u, v V A B F D E C G

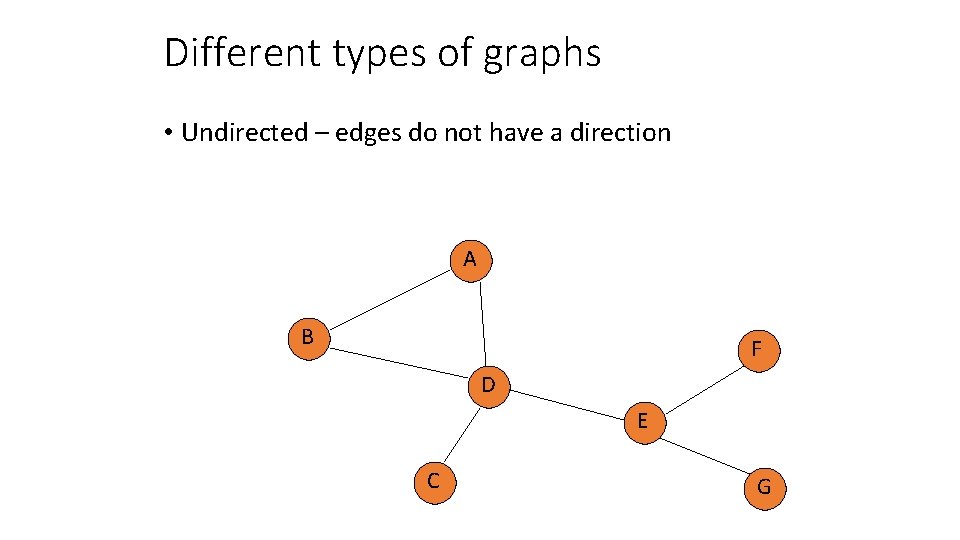
Different types of graphs • Undirected – edges do not have a direction A B F D E C G

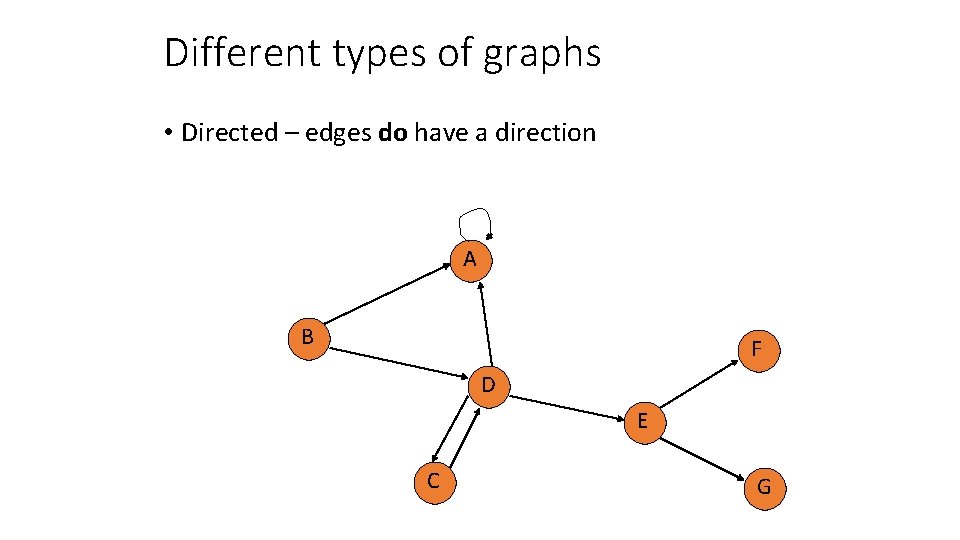
Different types of graphs • Directed – edges do have a direction A B F D E C G

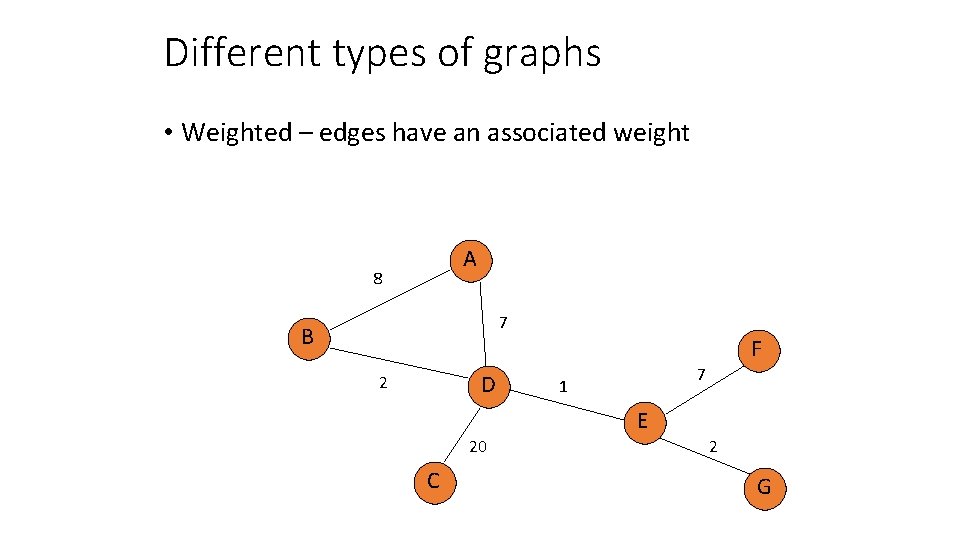
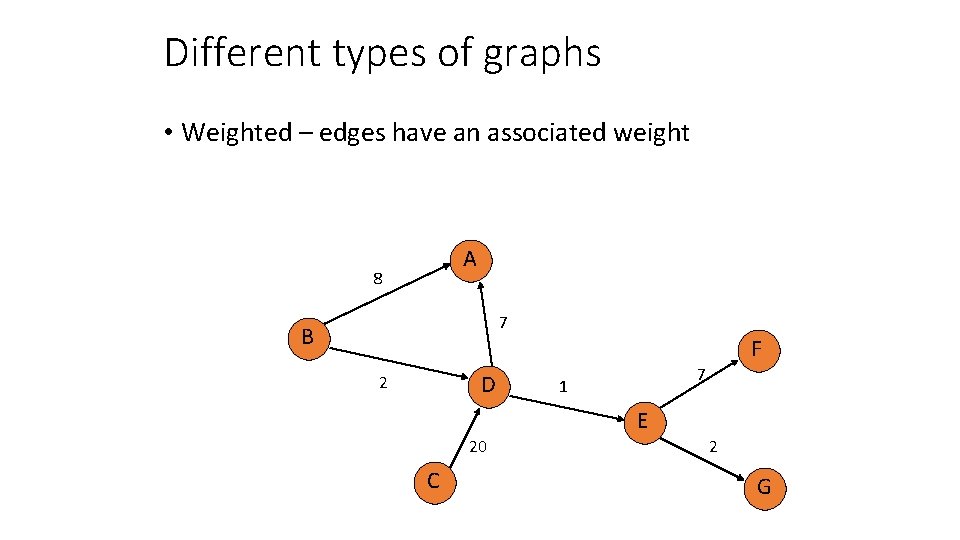
Different types of graphs • Weighted – edges have an associated weight A 8 7 B F D 2 7 1 E 20 C 2 G

Different types of graphs • Weighted – edges have an associated weight A 8 7 B F D 2 7 1 E 20 C 2 G

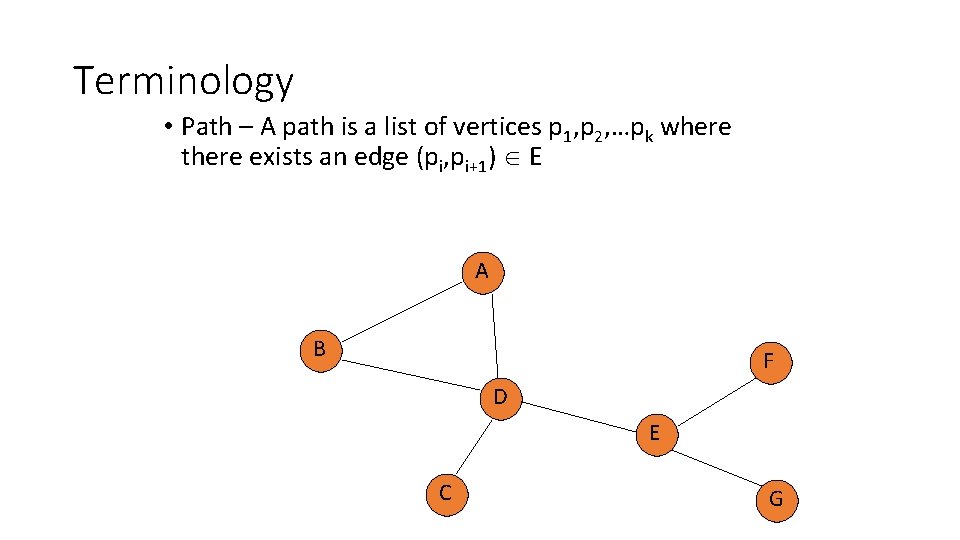
Terminology • Path – A path is a list of vertices p 1, p 2, …pk where there exists an edge (pi, pi+1) E A B F D E C G

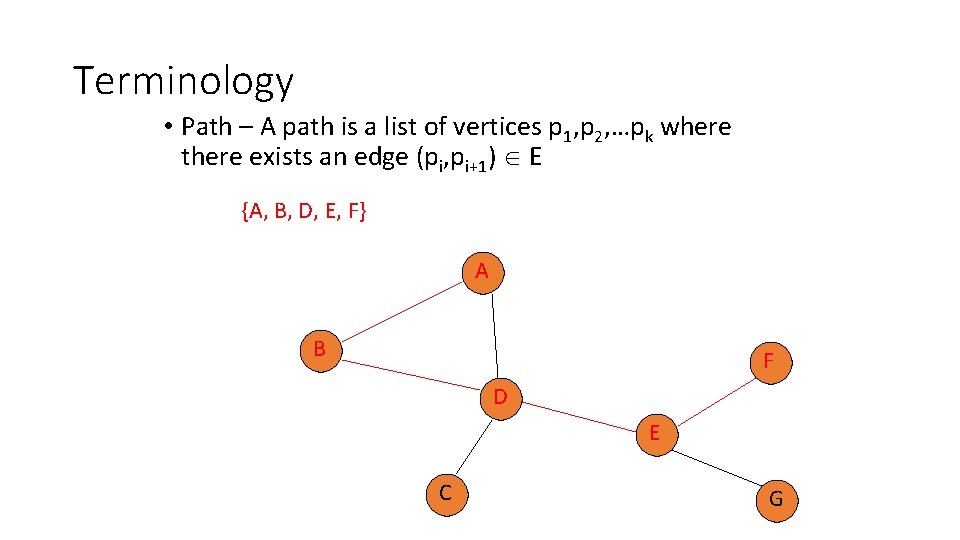
Terminology • Path – A path is a list of vertices p 1, p 2, …pk where there exists an edge (pi, pi+1) E {A, B, D, E, F} A B F D E C G

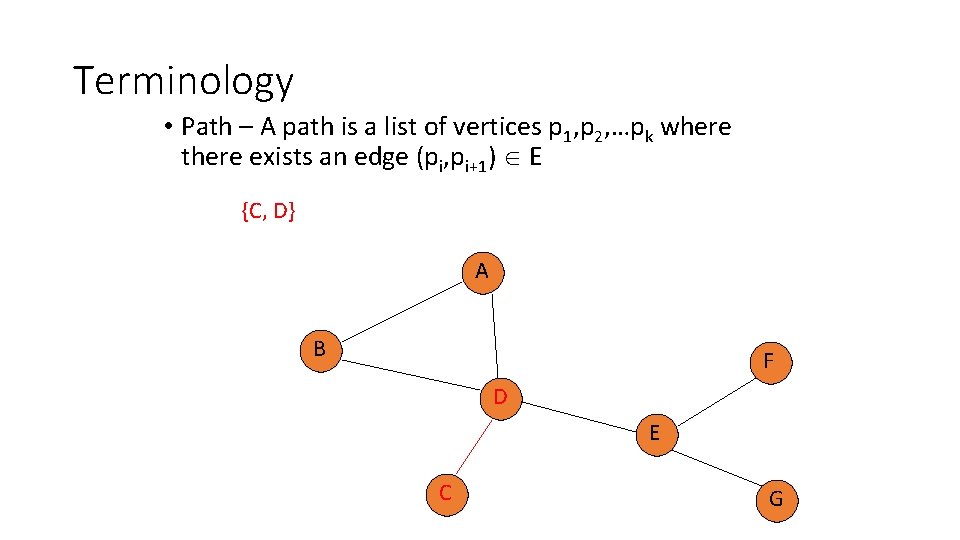
Terminology • Path – A path is a list of vertices p 1, p 2, …pk where there exists an edge (pi, pi+1) E {C, D} A B F D E C G

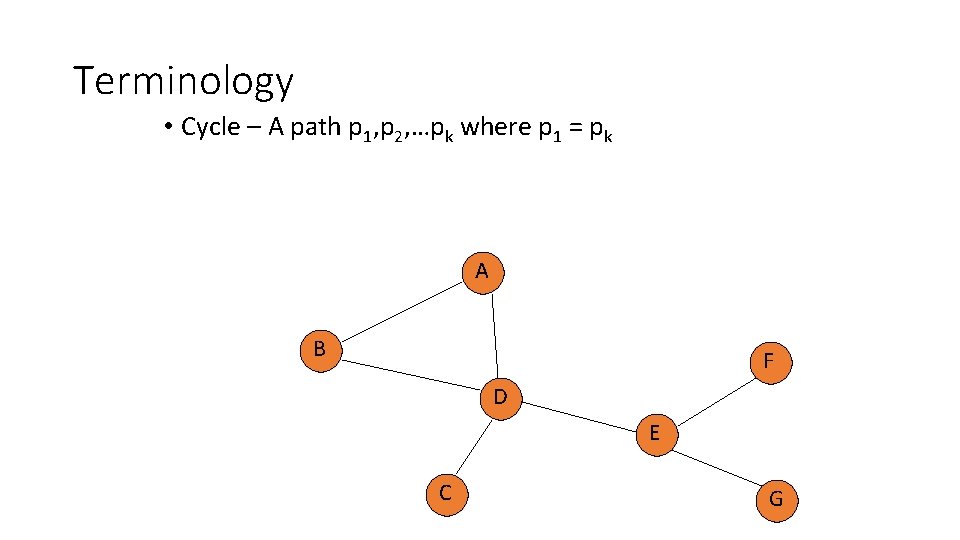
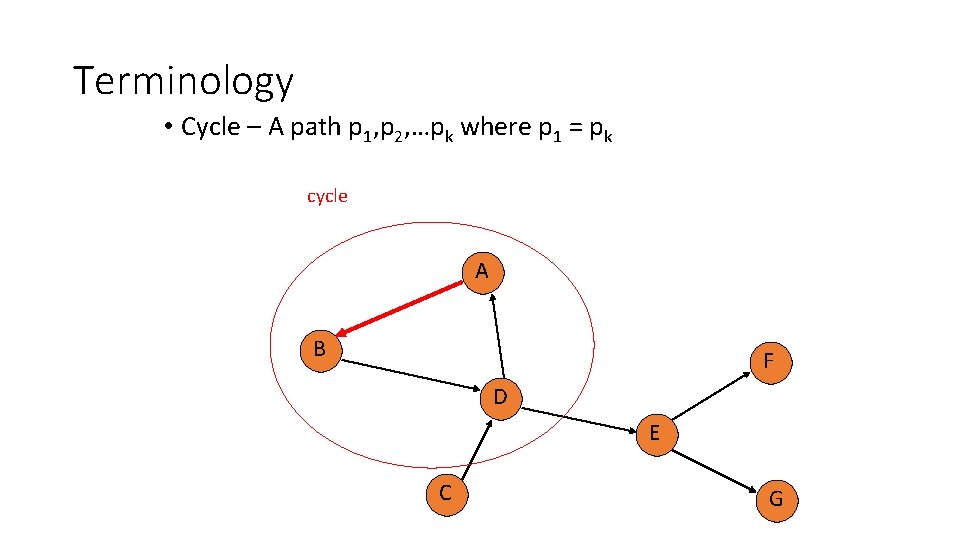
Terminology • Cycle – A path p 1, p 2, …pk where p 1 = pk A B F D E C G

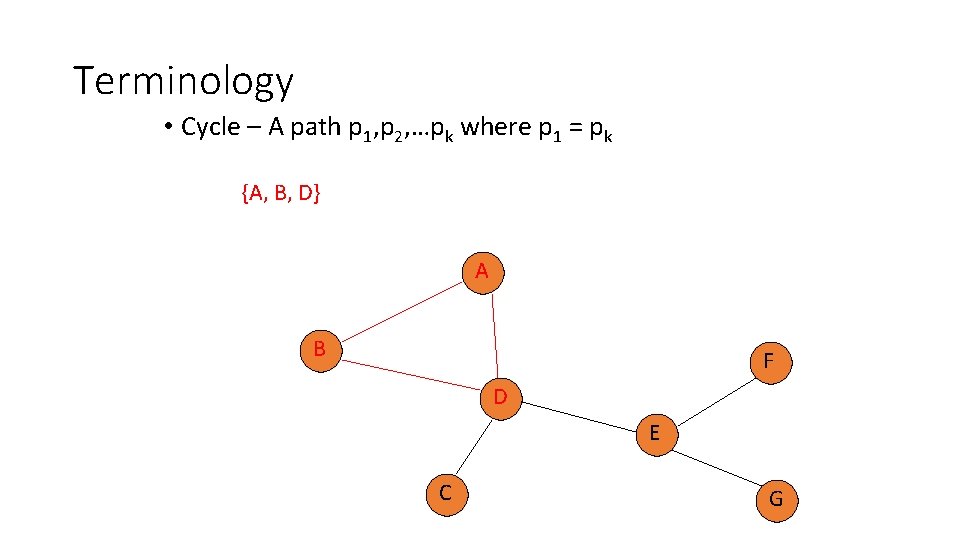
Terminology • Cycle – A path p 1, p 2, …pk where p 1 = pk {A, B, D} A B F D E C G

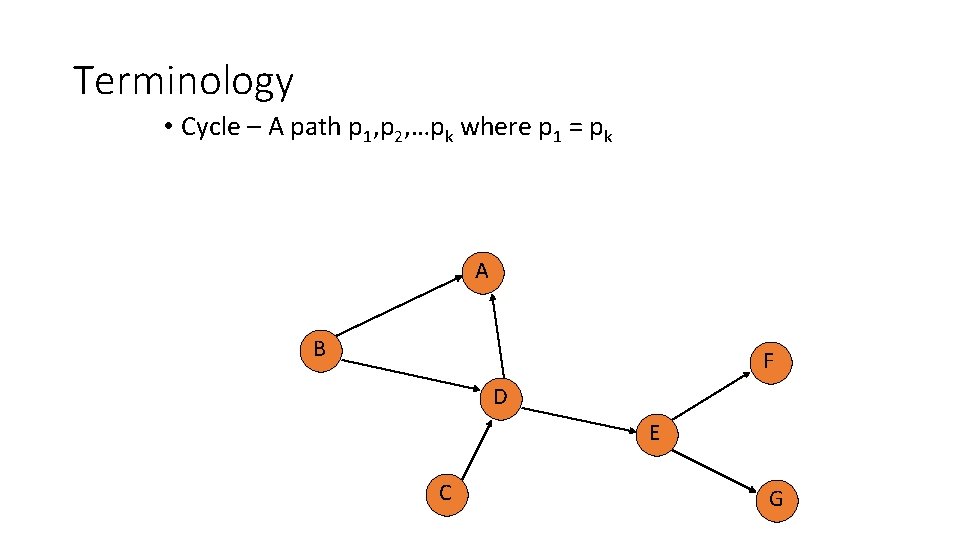
Terminology • Cycle – A path p 1, p 2, …pk where p 1 = pk A B F D E C G

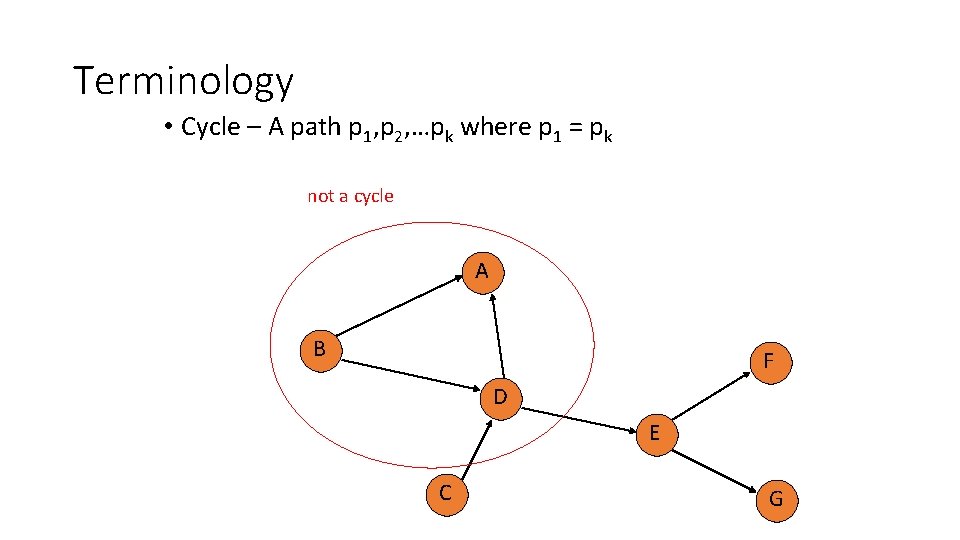
Terminology • Cycle – A path p 1, p 2, …pk where p 1 = pk not a cycle A B F D E C G

Terminology • Cycle – A path p 1, p 2, …pk where p 1 = pk cycle A B F D E C G

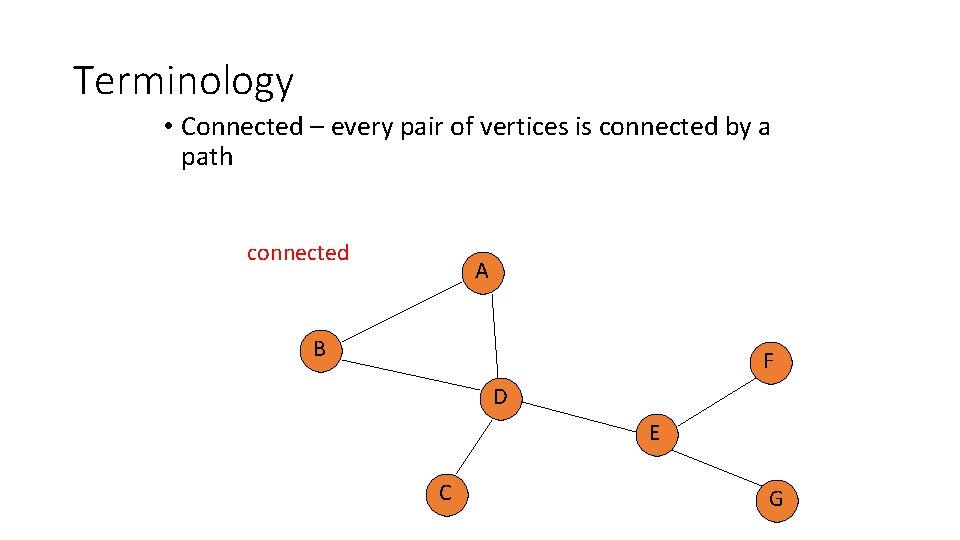
Terminology • Connected – every pair of vertices is connected by a path connected A B F D E C G

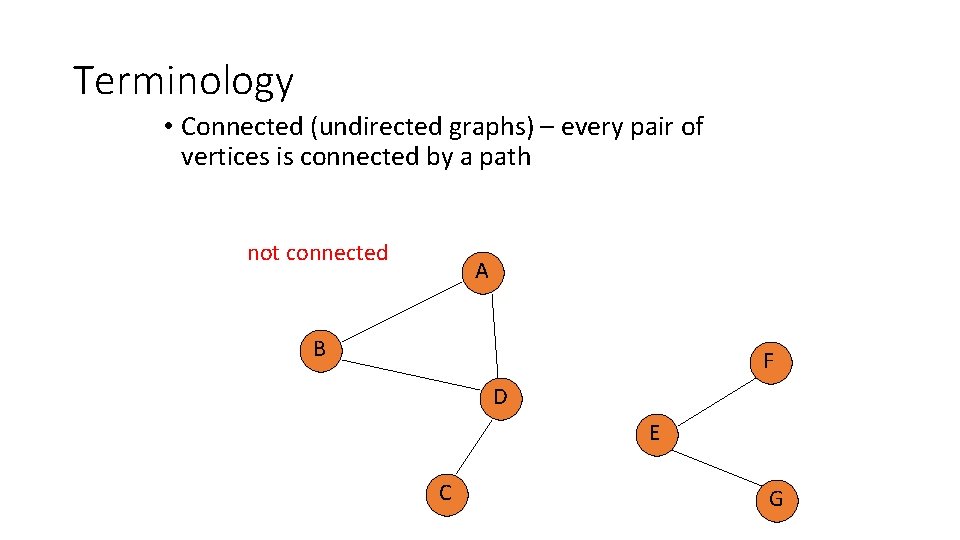
Terminology • Connected (undirected graphs) – every pair of vertices is connected by a path not connected A B F D E C G

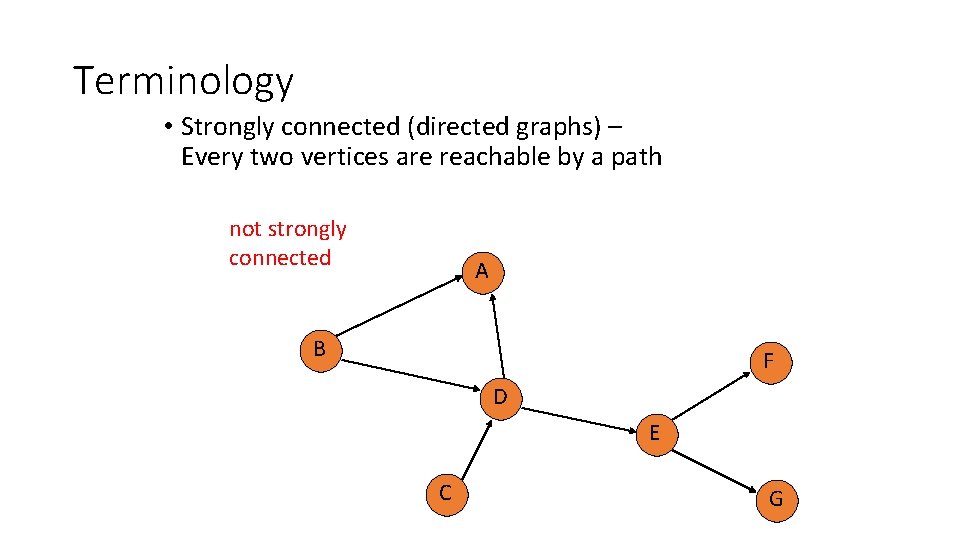
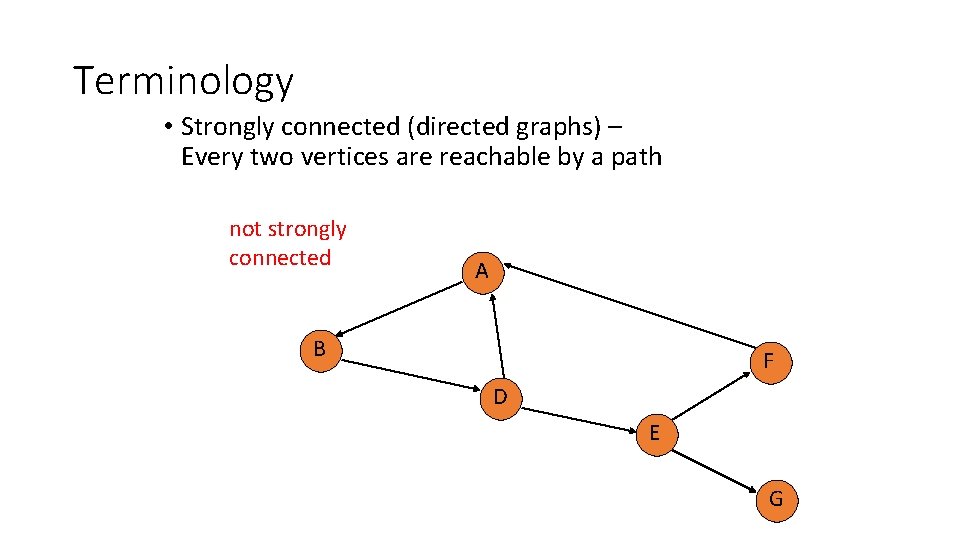
Terminology • Strongly connected (directed graphs) – Every two vertices are reachable by a path not strongly connected A B F D E C G

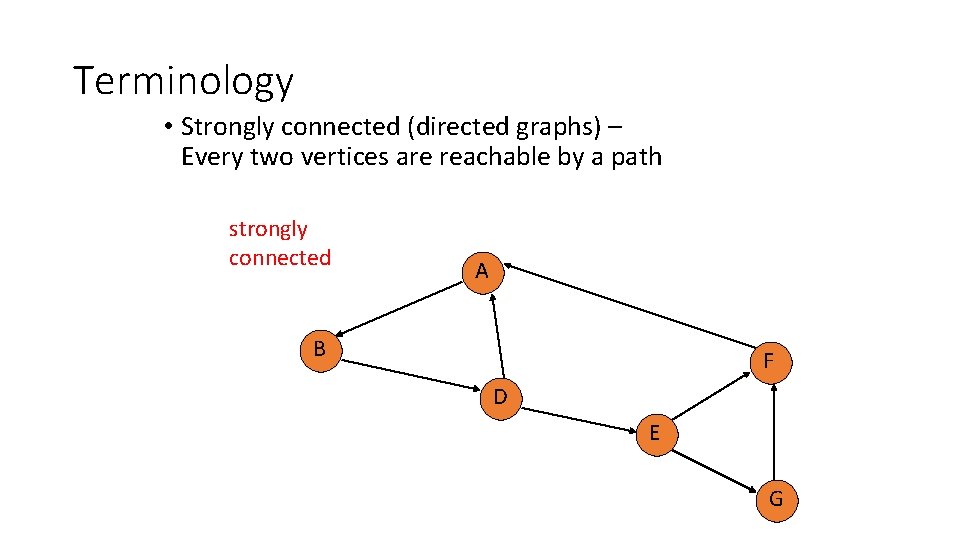
Terminology • Strongly connected (directed graphs) – Every two vertices are reachable by a path not strongly connected A B F D E G

Terminology • Strongly connected (directed graphs) – Every two vertices are reachable by a path strongly connected A B F D E G

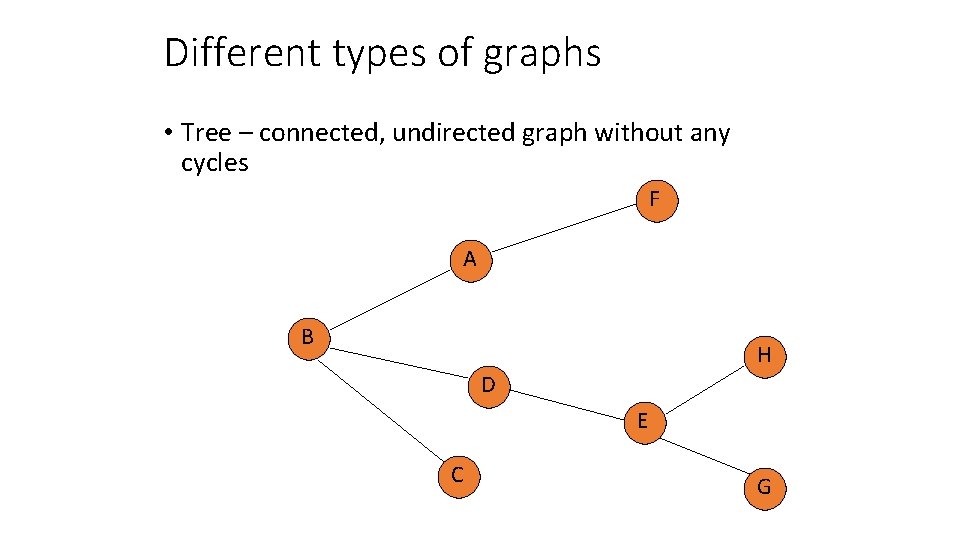
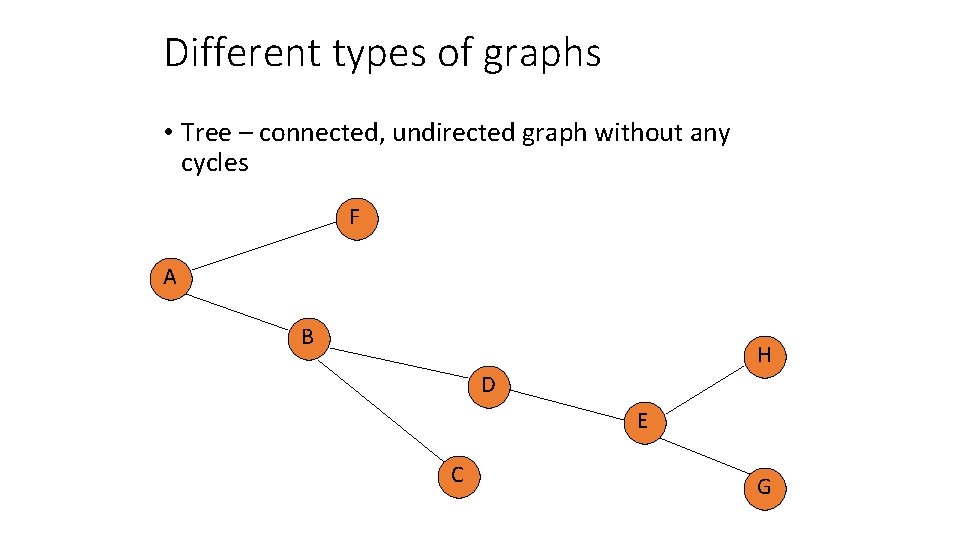
Different types of graphs • Tree – connected, undirected graph without any cycles F A B H D E C G

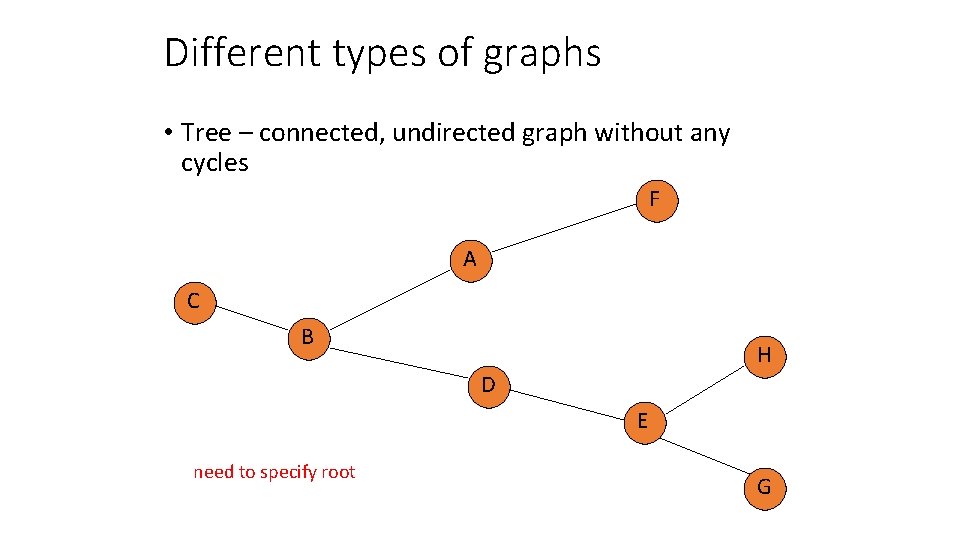
Different types of graphs • Tree – connected, undirected graph without any cycles F A C B H D E need to specify root G

Different types of graphs • Tree – connected, undirected graph without any cycles F A B H D E C G

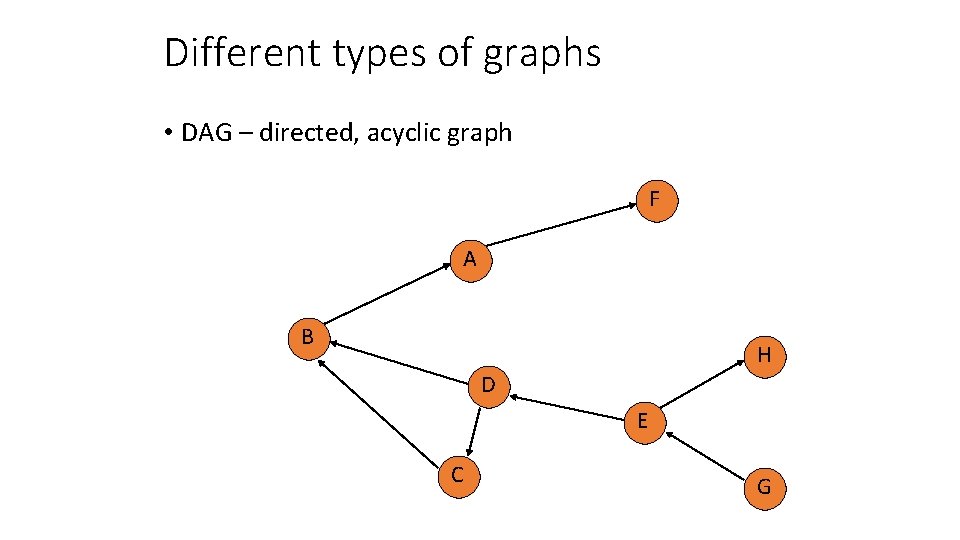
Different types of graphs • DAG – directed, acyclic graph F A B H D E C G

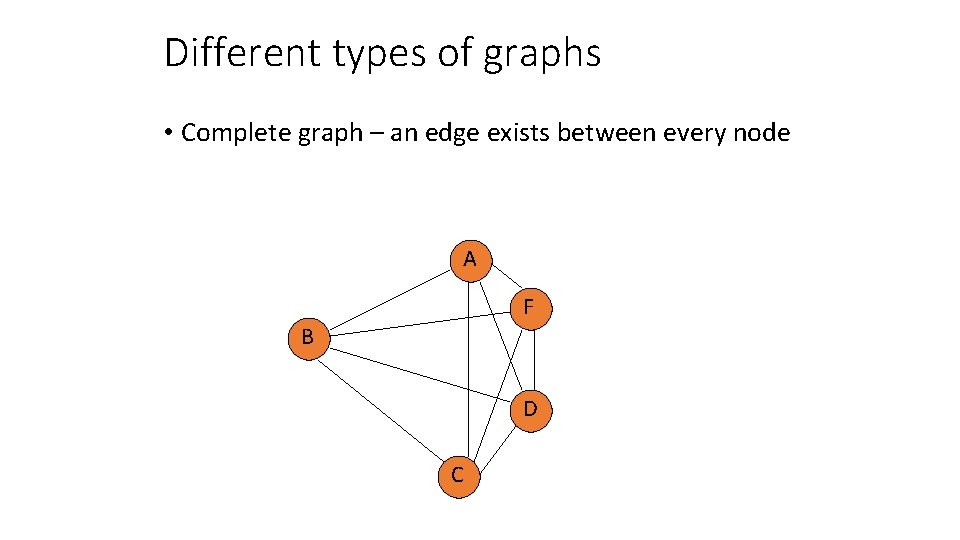
Different types of graphs • Complete graph – an edge exists between every node A F B D C

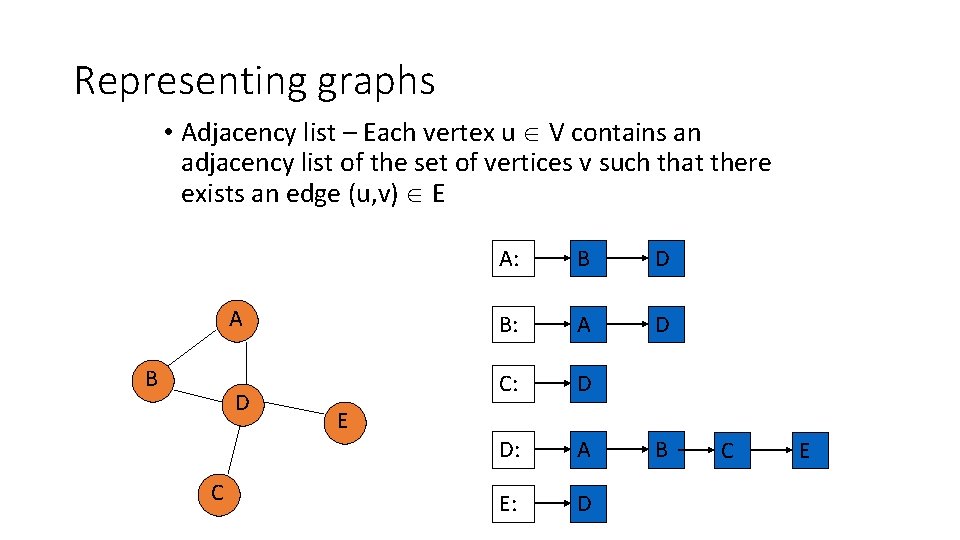
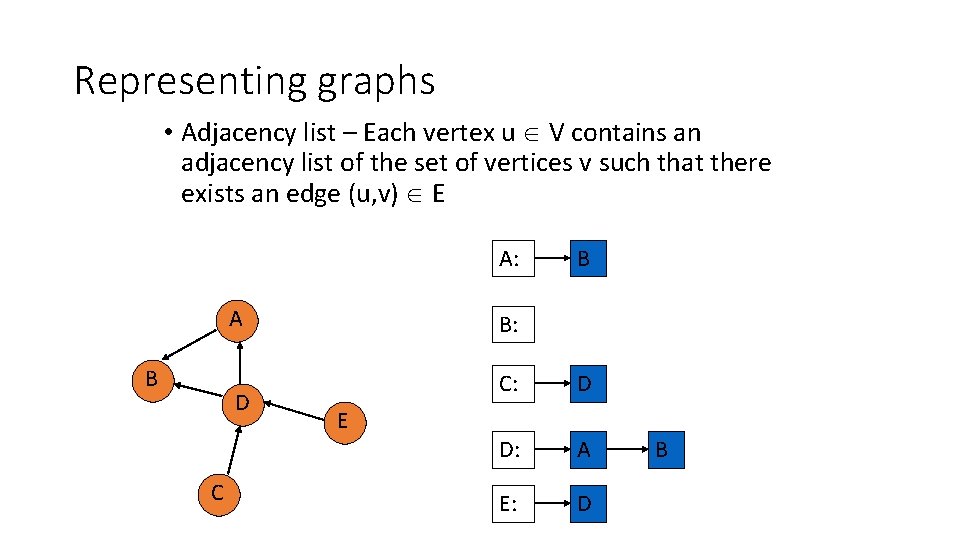
Representing graphs • Adjacency list – Each vertex u V contains an adjacency list of the set of vertices v such that there exists an edge (u, v) E A B D C E A: B D B: A D C: D D: A E: D B C E

Representing graphs • Adjacency list – Each vertex u V contains an adjacency list of the set of vertices v such that there exists an edge (u, v) E A: A B D C B B: E C: D D: A E: D B

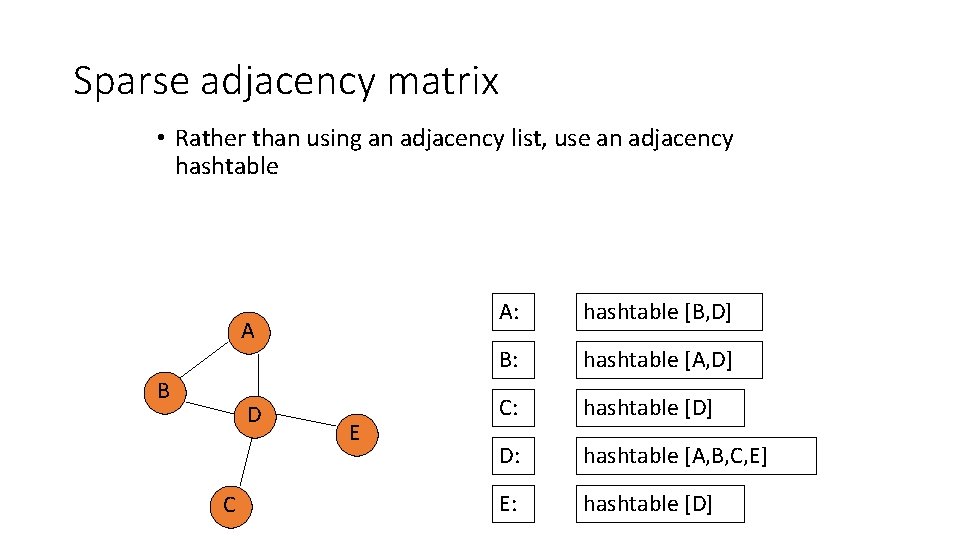
Sparse adjacency matrix • Rather than using an adjacency list, use an adjacency hashtable A B D C E A: hashtable [B, D] B: hashtable [A, D] C: hashtable [D] D: hashtable [A, B, C, E] E: hashtable [D]

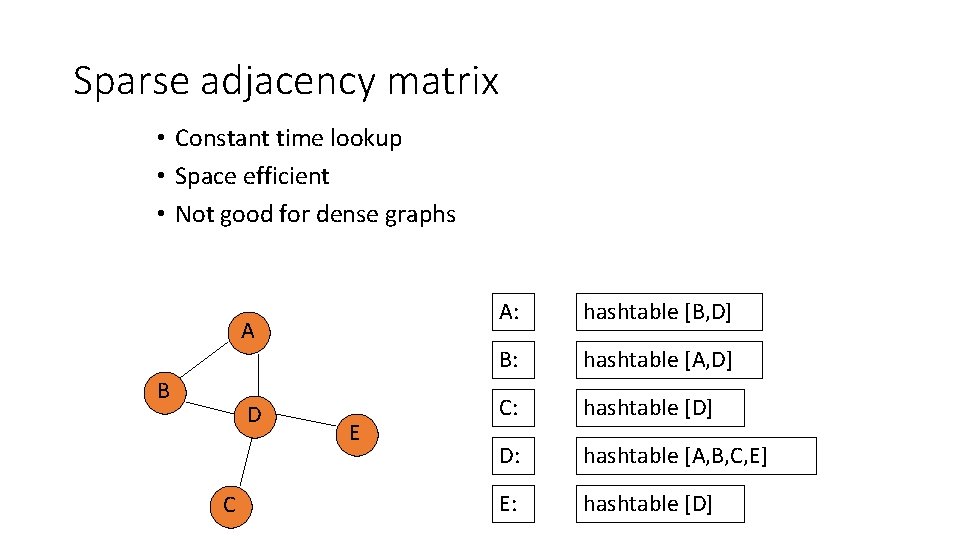
Sparse adjacency matrix • Constant time lookup • Space efficient • Not good for dense graphs A B D C E A: hashtable [B, D] B: hashtable [A, D] C: hashtable [D] D: hashtable [A, B, C, E] E: hashtable [D]

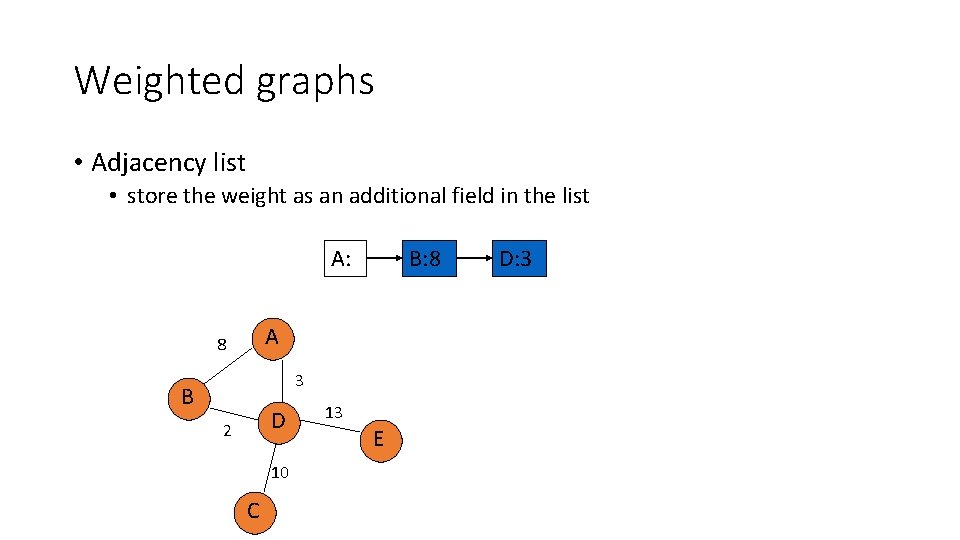
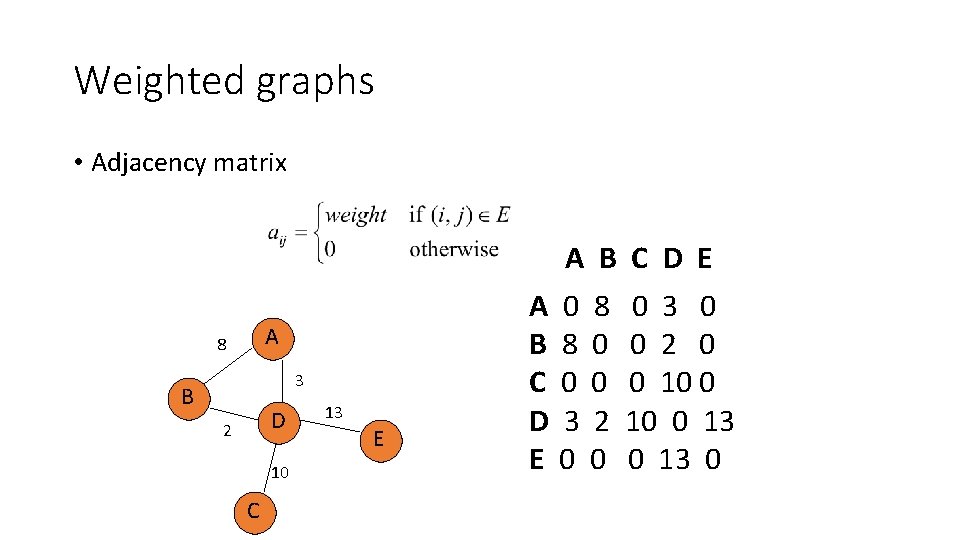
Weighted graphs • Adjacency list • store the weight as an additional field in the list A: B: 8 A 8 3 B D 2 10 C 13 E D: 3

Weighted graphs • Adjacency matrix A B C D E A 8 3 B D 2 10 C 13 E A B C D E 0 8 0 3 0 8 0 0 2 0 0 3 0 0 2 0 0 10 0 13 0

Graph algorithms/questions • Graph traversal (BFS, DFS) • Shortest path from a to b • unweighted • weighted positive weights • negative/positive weights • Minimum spanning trees • Are all nodes in the graph connected? • Is the graph bipartite?

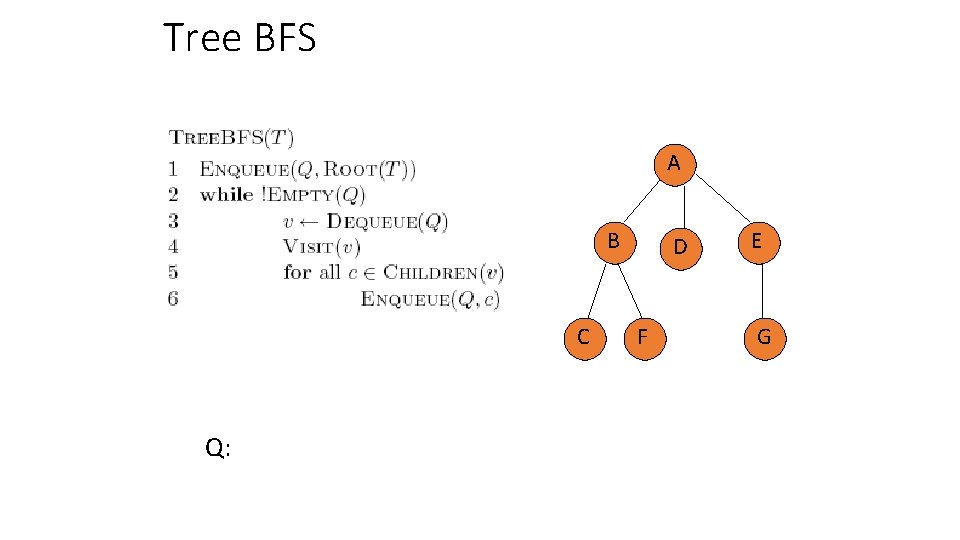
Breadth First Search (BFS) on Trees

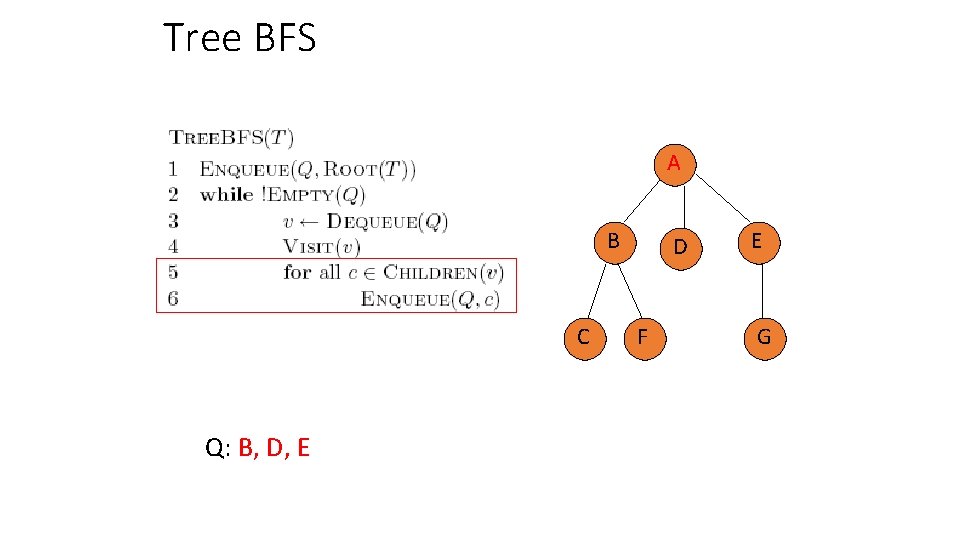
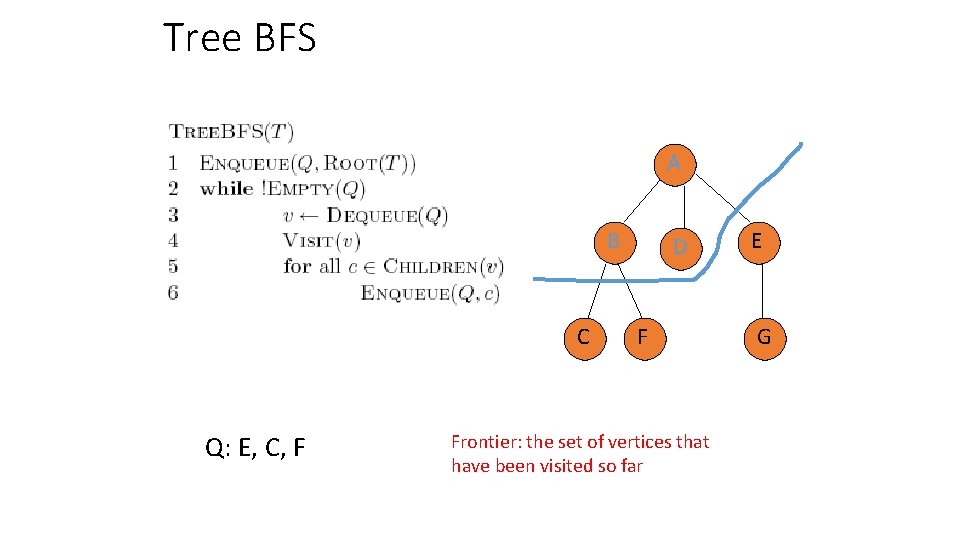
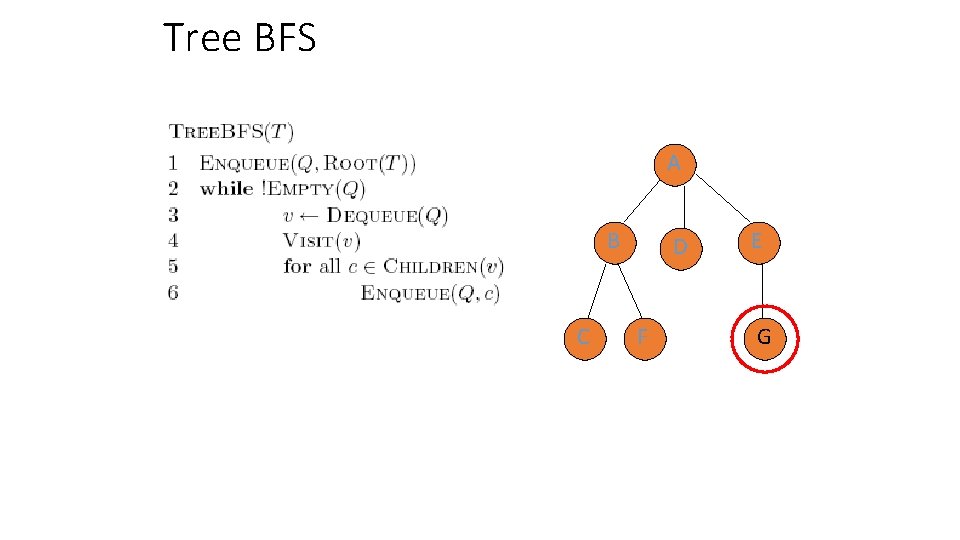
Tree BFS A B C Q: D F E G

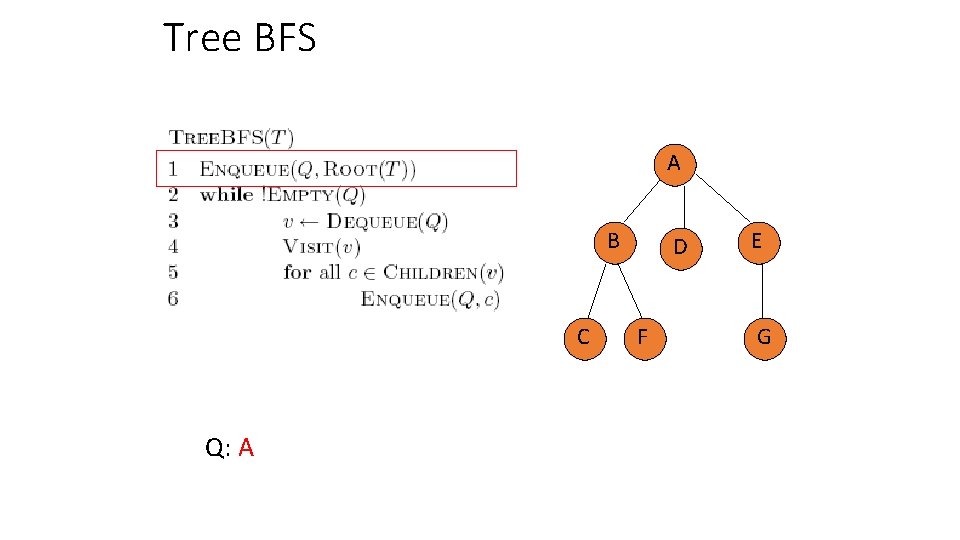
Tree BFS A B C Q: A D F E G

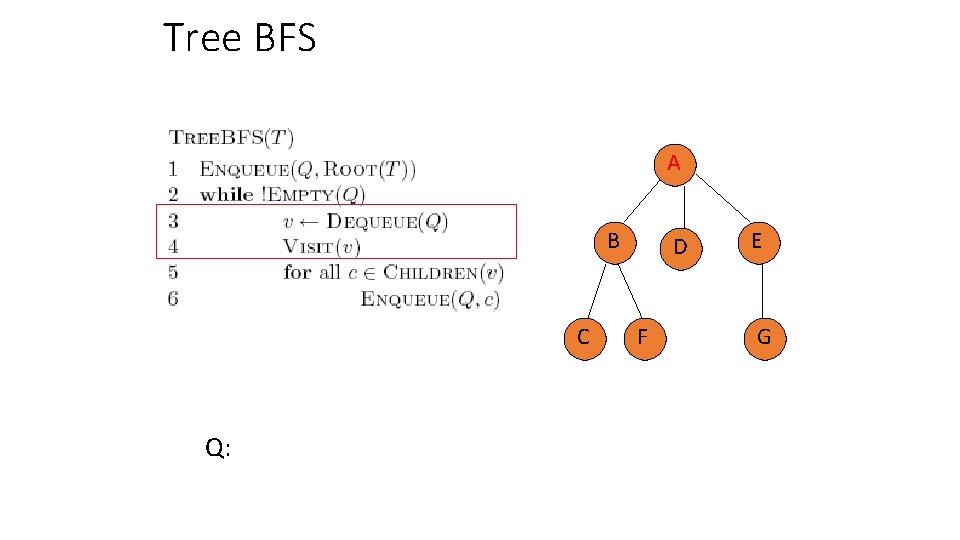
Tree BFS A B C Q: D F E G

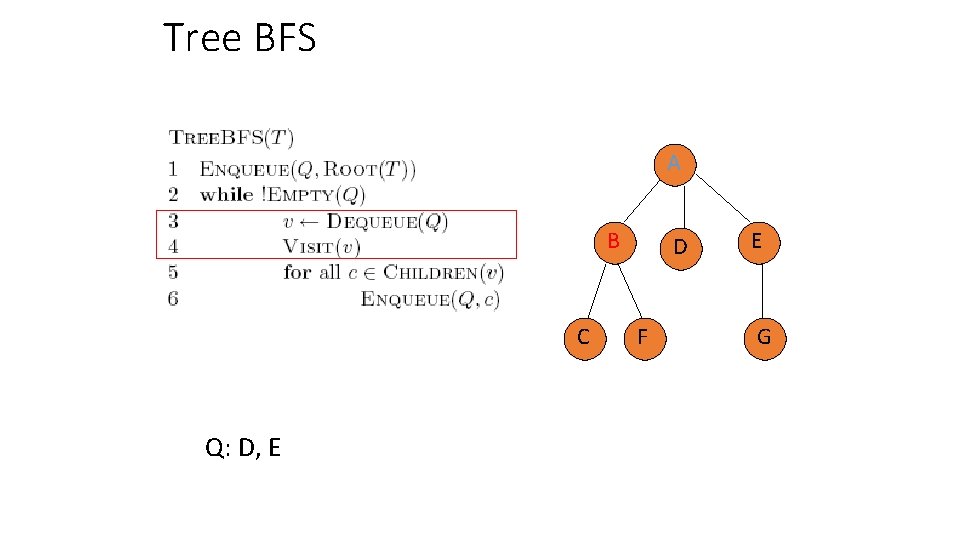
Tree BFS A B C Q: B, D, E D F E G

Tree BFS A B C Q: D, E D F E G

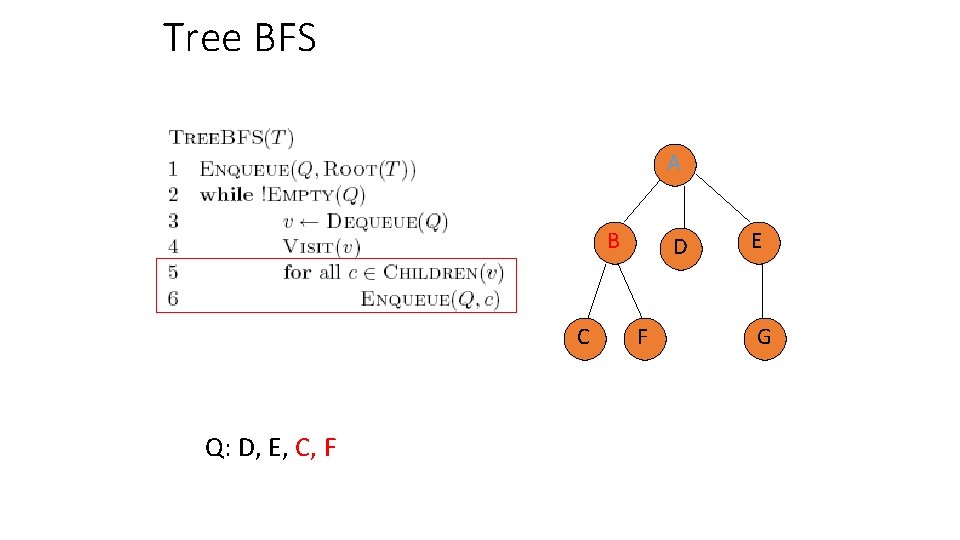
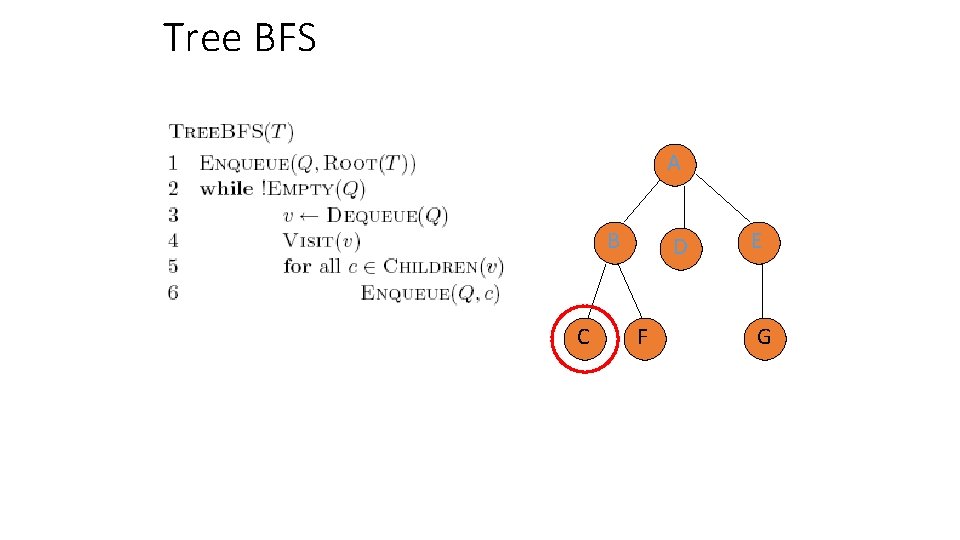
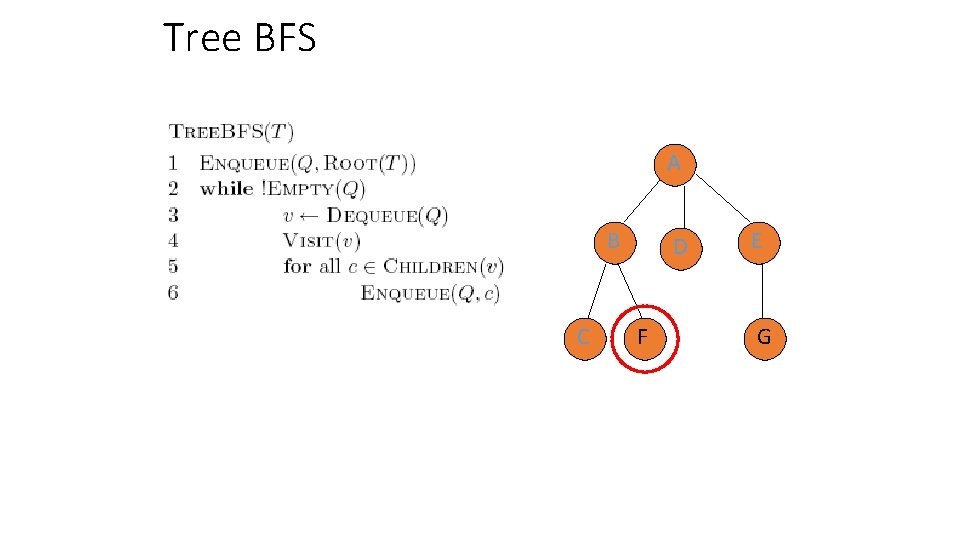
Tree BFS A B C Q: D, E, C, F D F E G

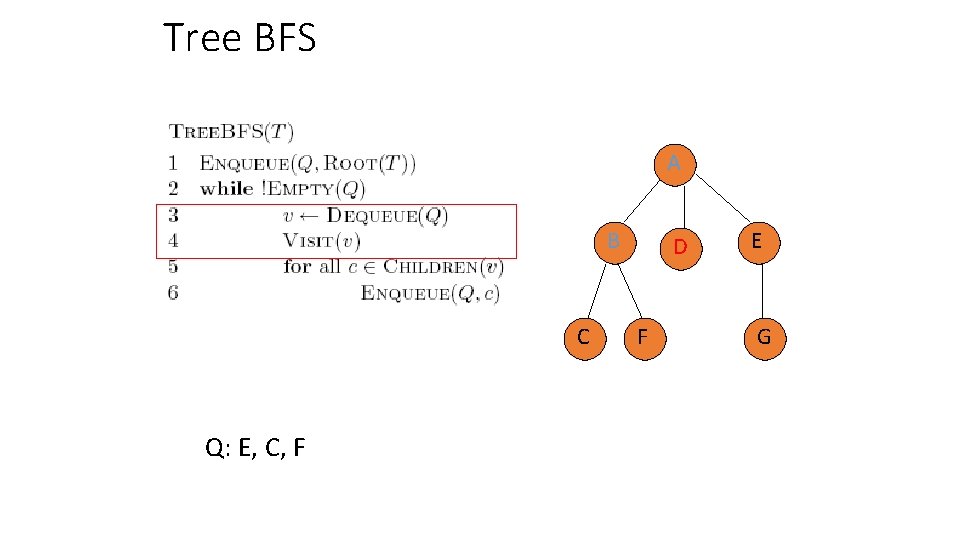
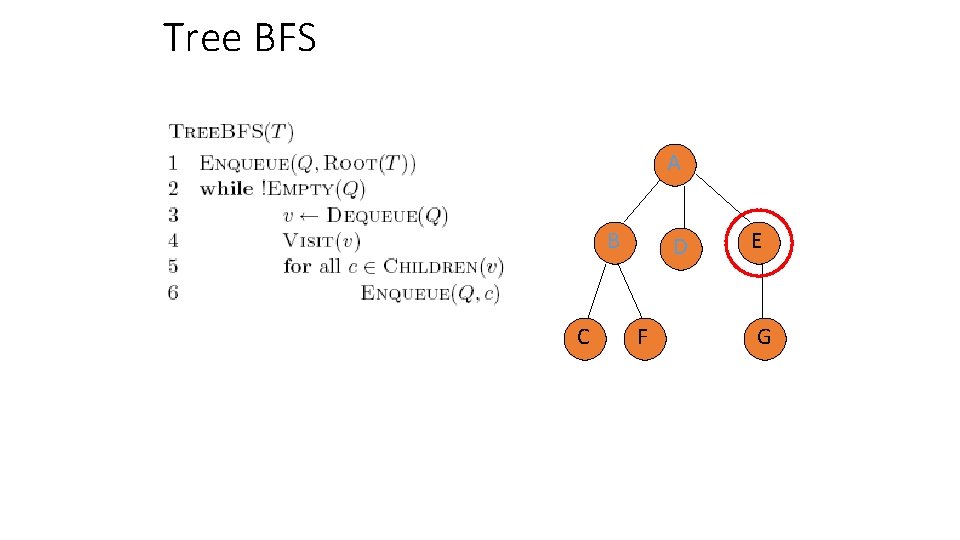
Tree BFS A B C Q: E, C, F D F E G

Tree BFS A B C Q: E, C, F D F Frontier: the set of vertices that have been visited so far E G

Tree BFS A B C D F E G

Tree BFS A B C D F E G

Tree BFS A B C D F E G

Tree BFS A B C D F E G

Tree BFS • What order does the algorithm traverse the nodes? • BFS traversal visits the nodes in increasing distance from the root

Tree BFS • Does it visit all of the nodes?

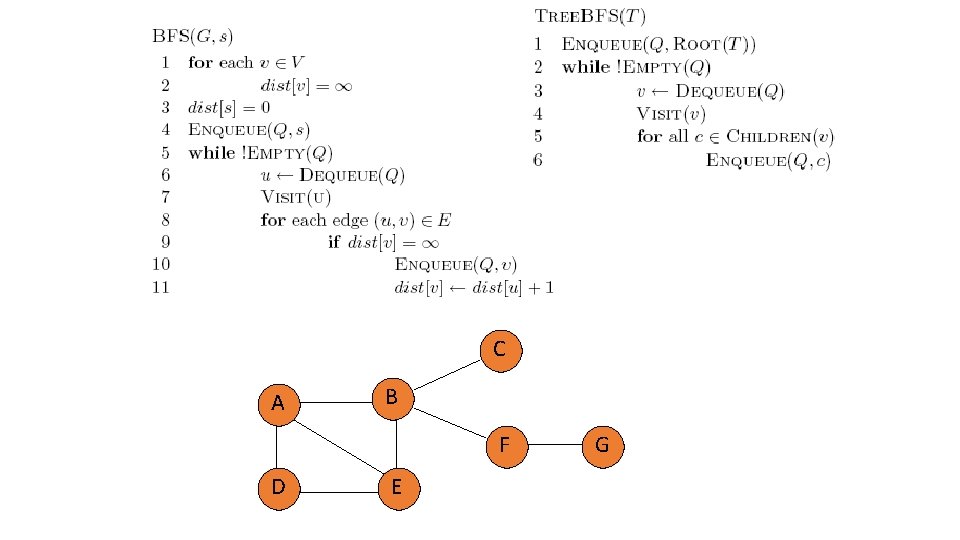
Running time of Tree BFS • Adjacency list • How many times does it visit each vertex? • How many times is each edge traversed? • O(|V|+|E|) • Adjacency matrix • For each vertex visited, how much work is done? • O(|V|2)

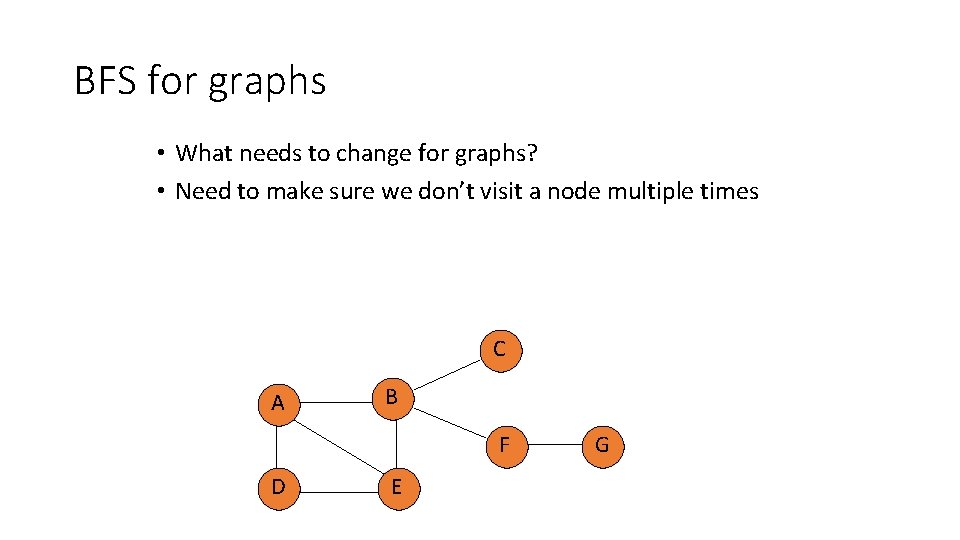
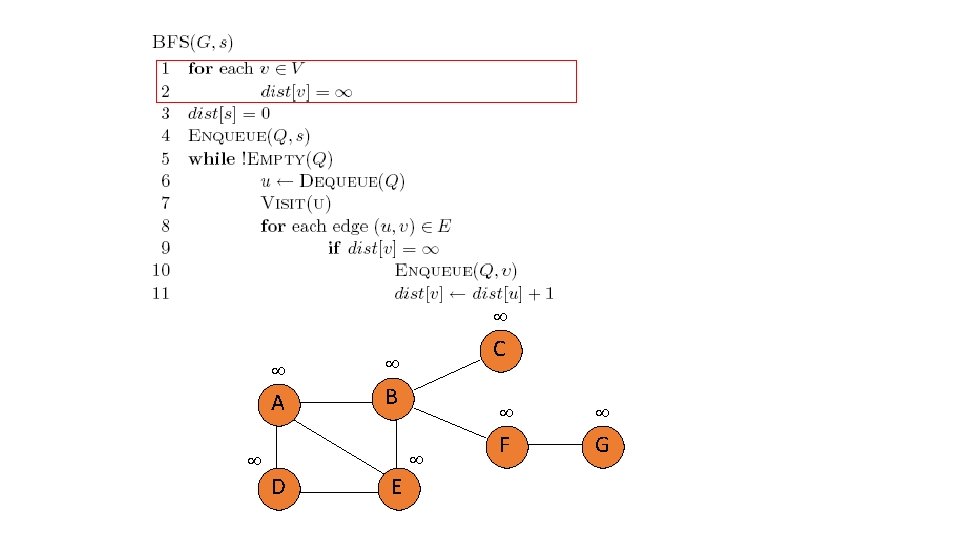
BFS for graphs • What needs to change for graphs? • Need to make sure we don’t visit a node multiple times C A B F D E G

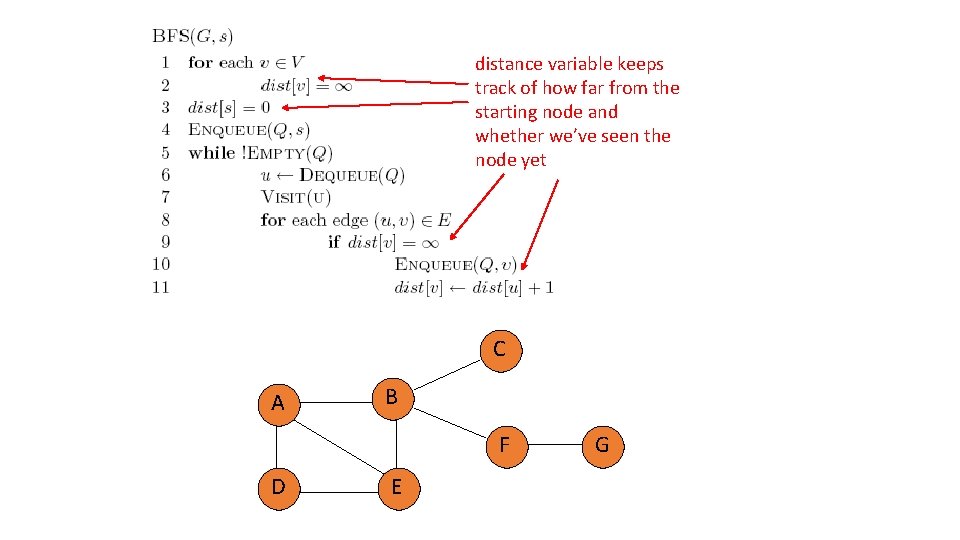
distance variable keeps track of how far from the starting node and whether we’ve seen the node yet C A B F D E G

C A B F D E G

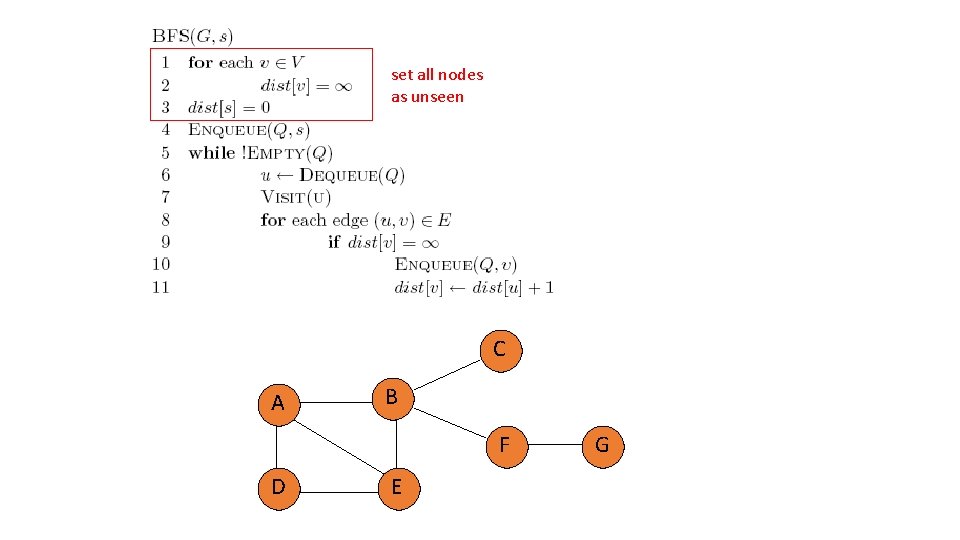
set all nodes as unseen C A B F D E G

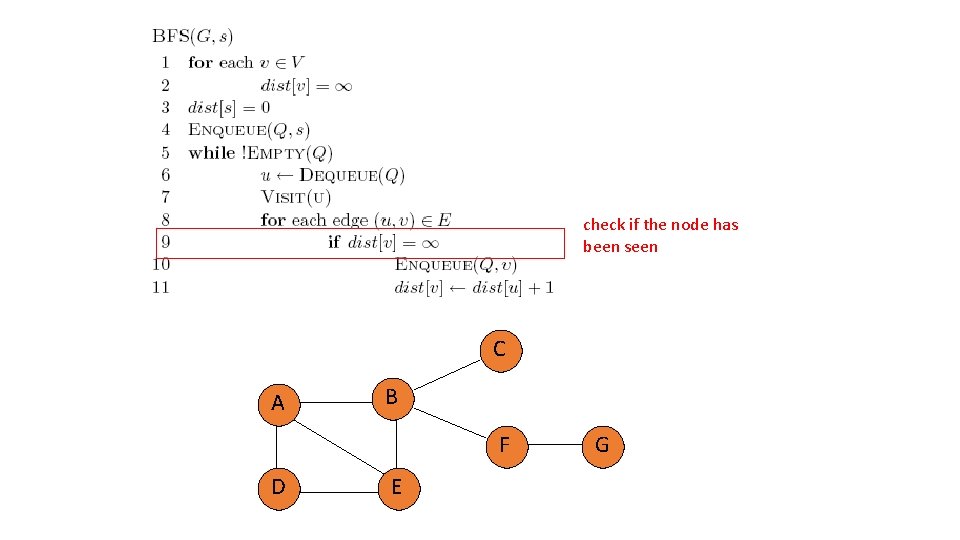
check if the node has been seen C A B F D E G

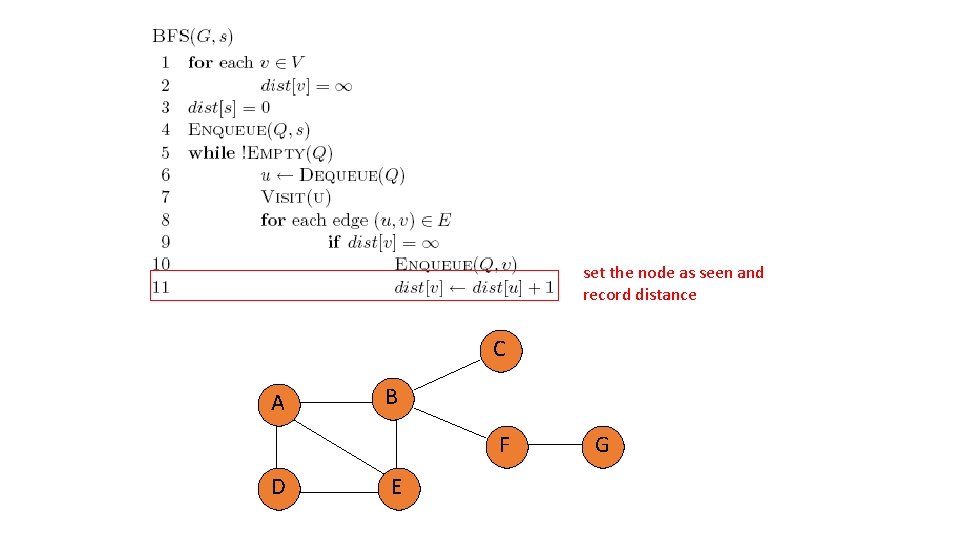
set the node as seen and record distance C A B F D E G

A C B D E F G

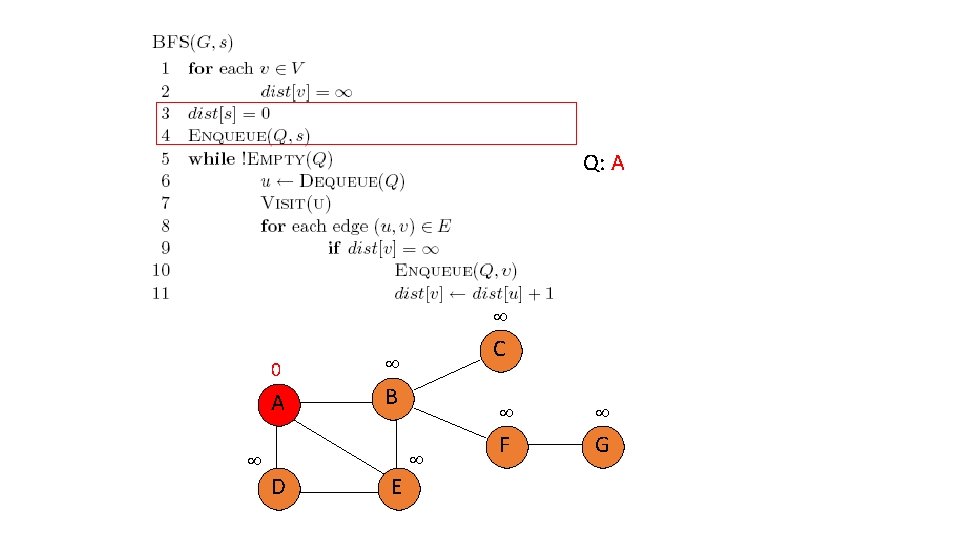
Q: A 0 A C B D E F G

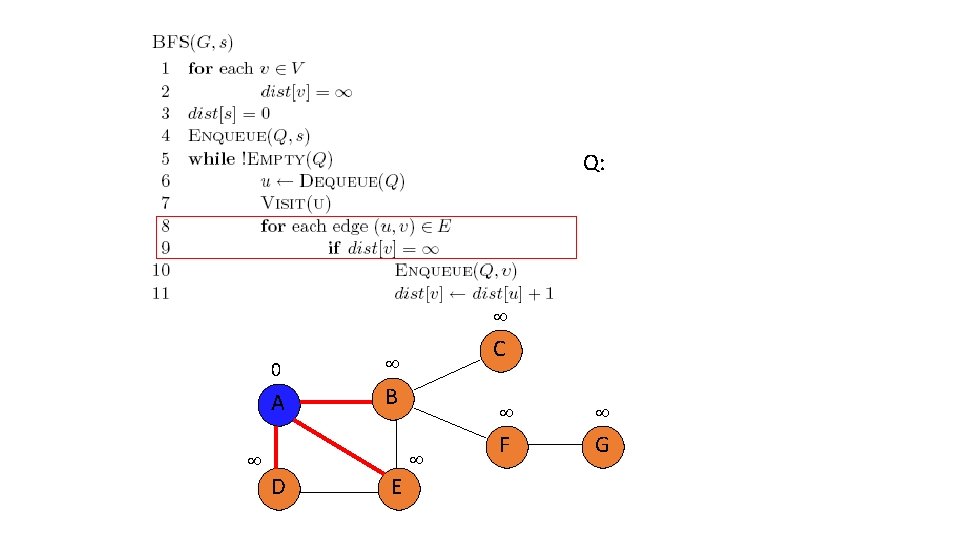
Q: 0 A C B D E F G

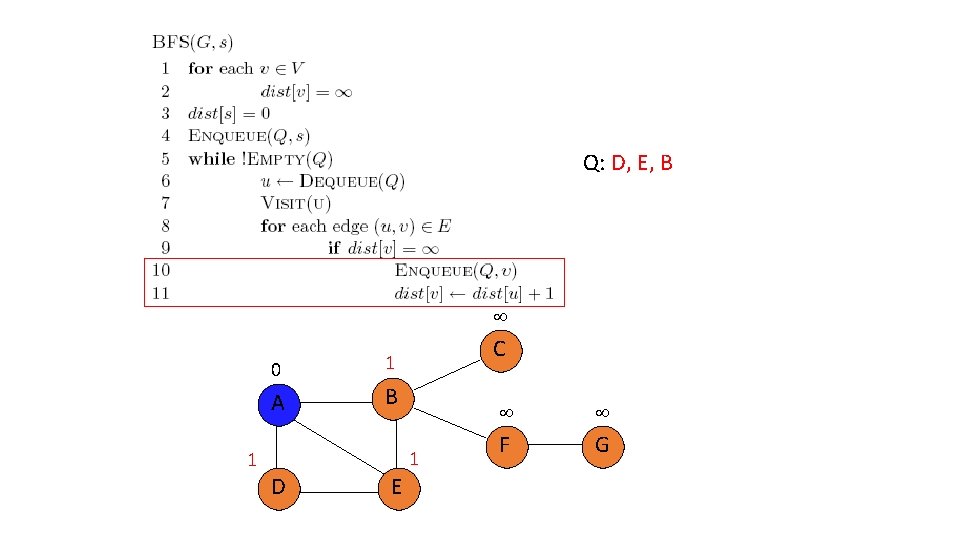
Q: D, E, B 0 A 1 C 1 B 1 D E F G

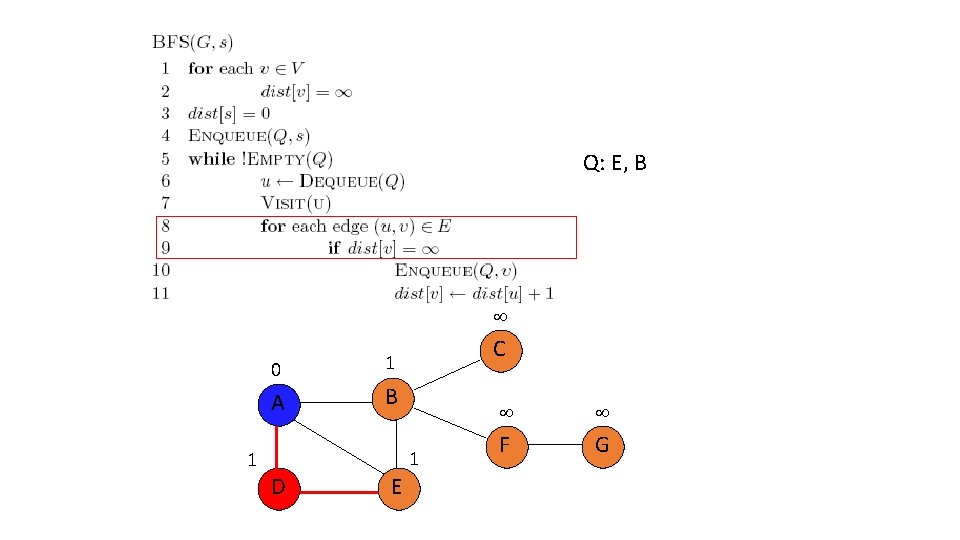
Q: E, B 0 A 1 C 1 B 1 D E F G

Q: B 0 A 1 C 1 B 1 D E F G

Q: B 0 A 1 C 1 B 1 D E F G

Q: 0 A 1 C 1 B 1 D E F G

Q: 0 A 1 C 1 B 1 D E F G

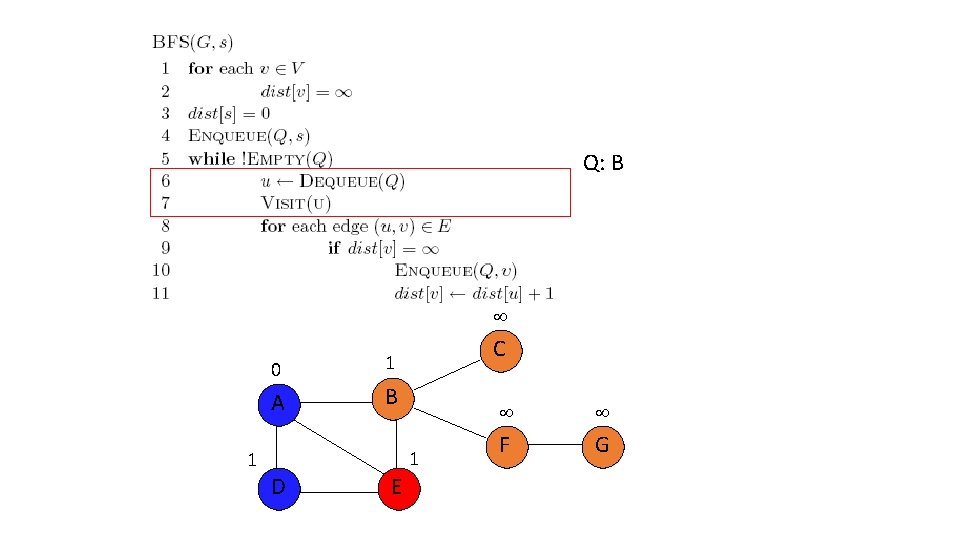
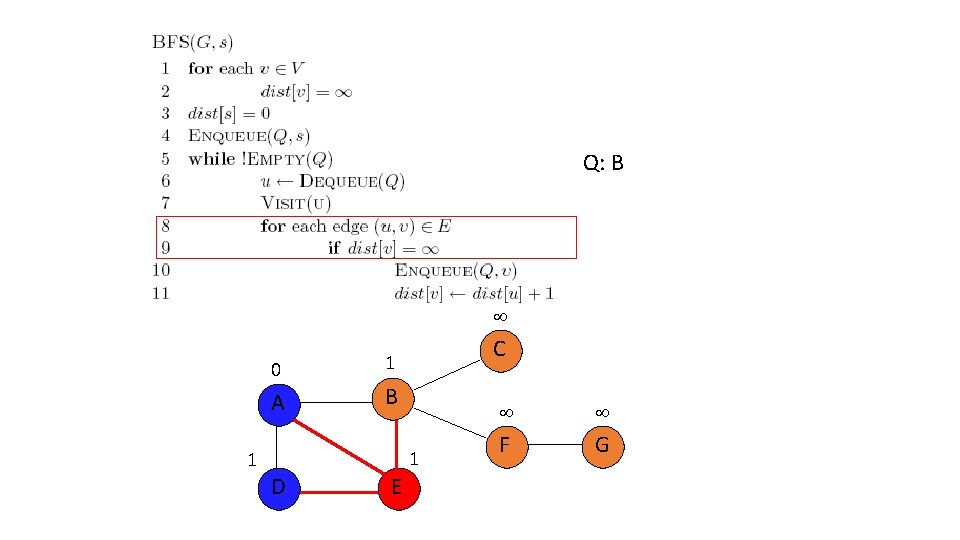
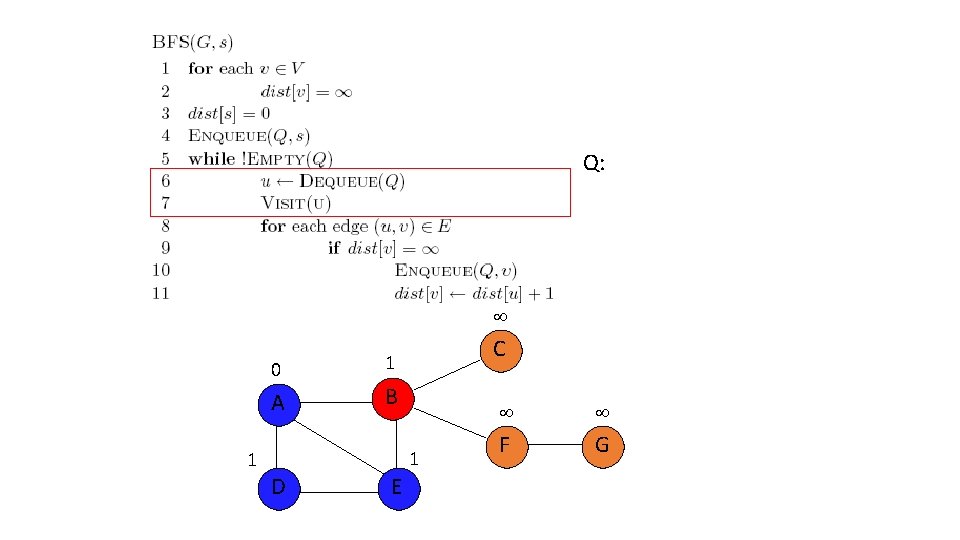
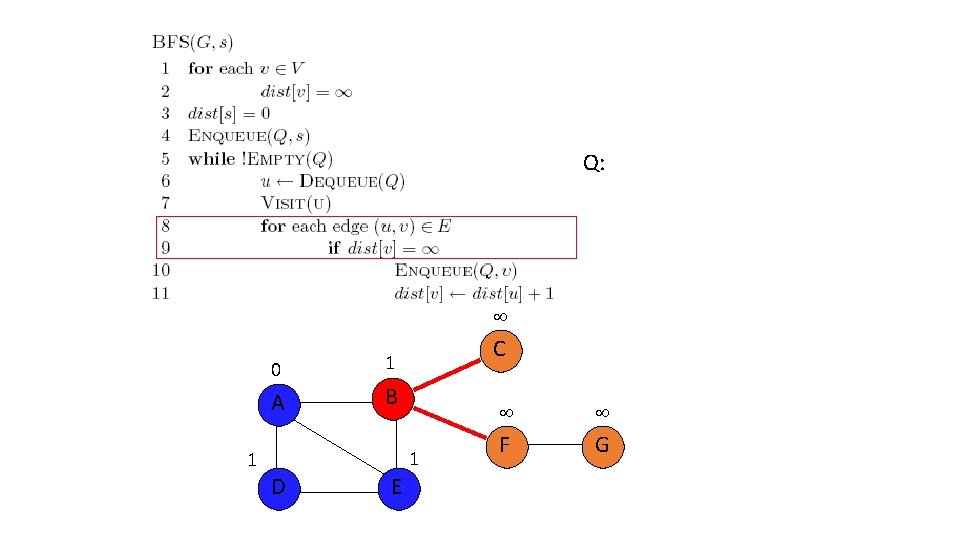
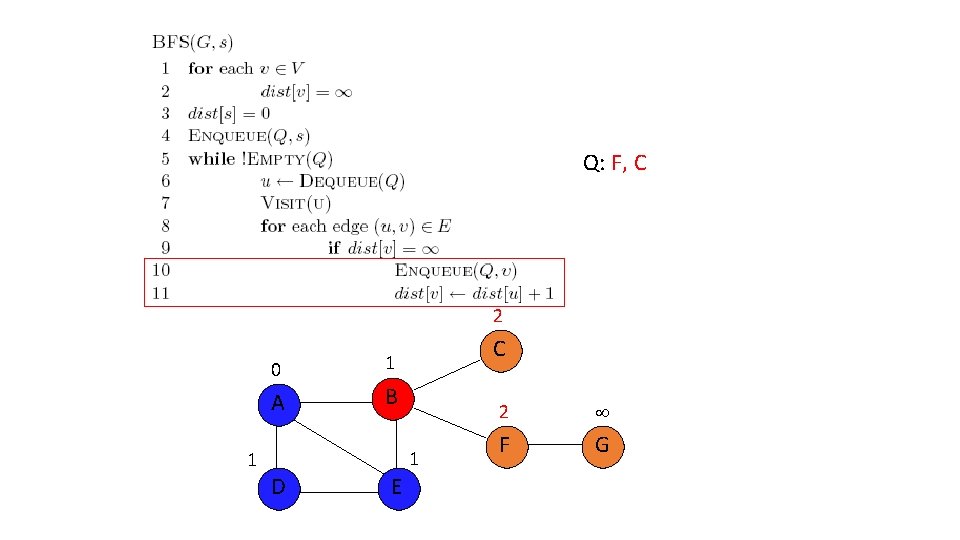
Q: F, C 2 0 A 1 C 1 B 1 D E 2 F G

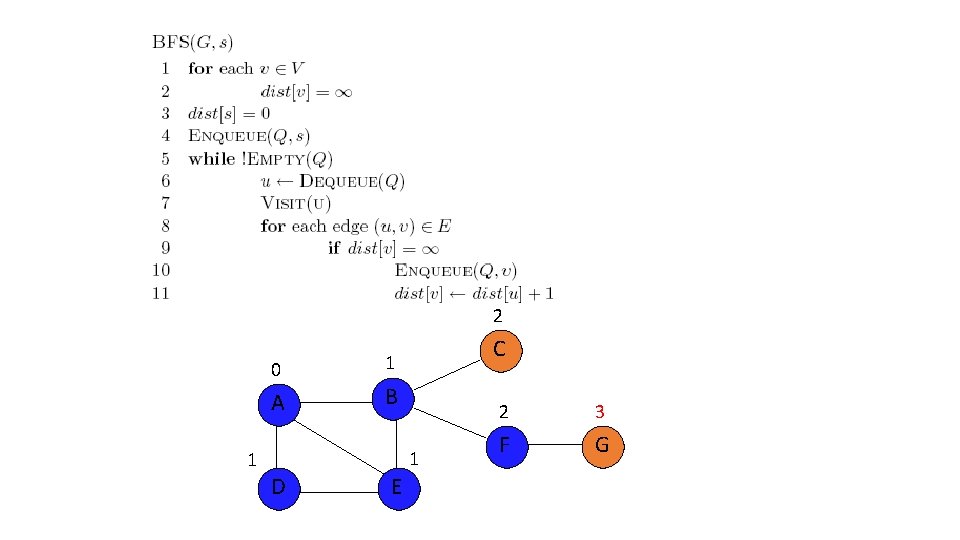
2 0 A 1 C 1 B 1 D E 2 3 F G

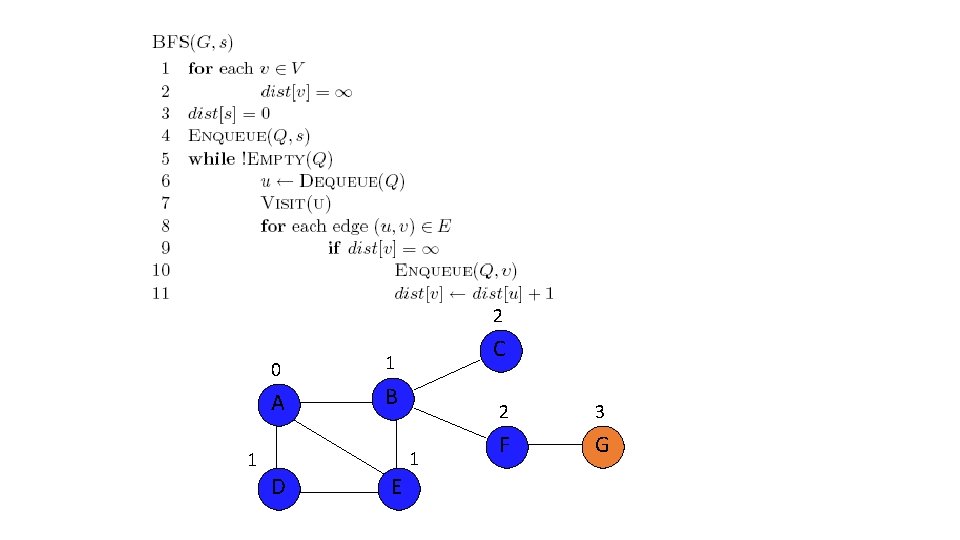
2 0 A 1 C 1 B 1 D E 2 3 F G

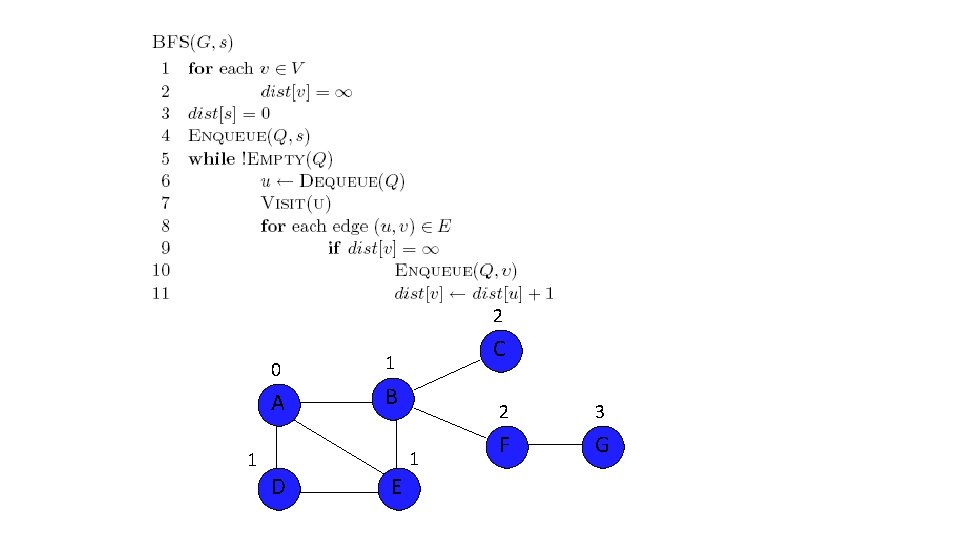
2 0 A 1 C 1 B 1 D E 2 3 F G

Runtime of BFS • Nothing changed over our analysis of Tree. BFS

Runtime of BFS • Adjacency list: O(|V| + |E|) • Adjacency matrix: O(|V|2)

Depth First Search (DFS)

Depth First Search (DFS)

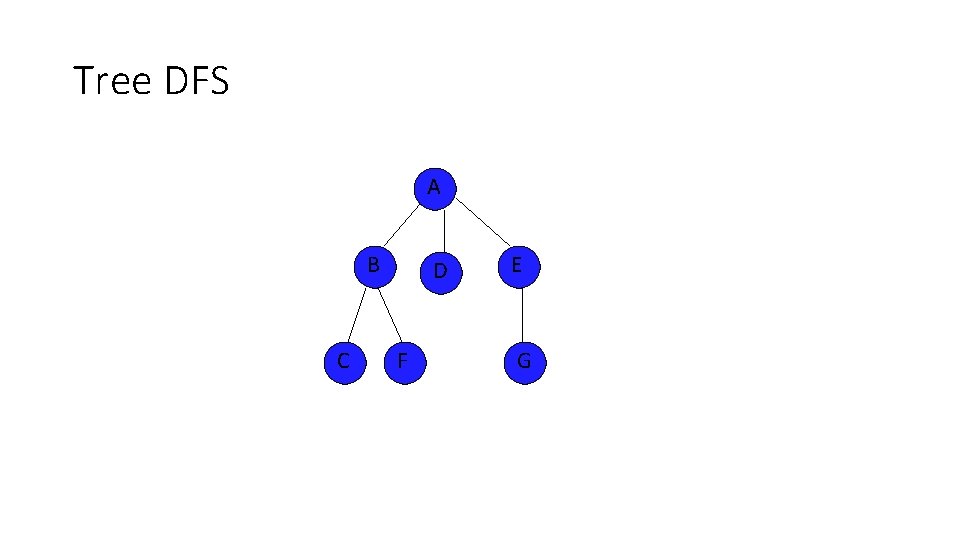
Tree DFS A B C D F E G

Tree DFS A B C D F E G

Tree DFS A B C D F E G

Tree DFS A B C D F E G

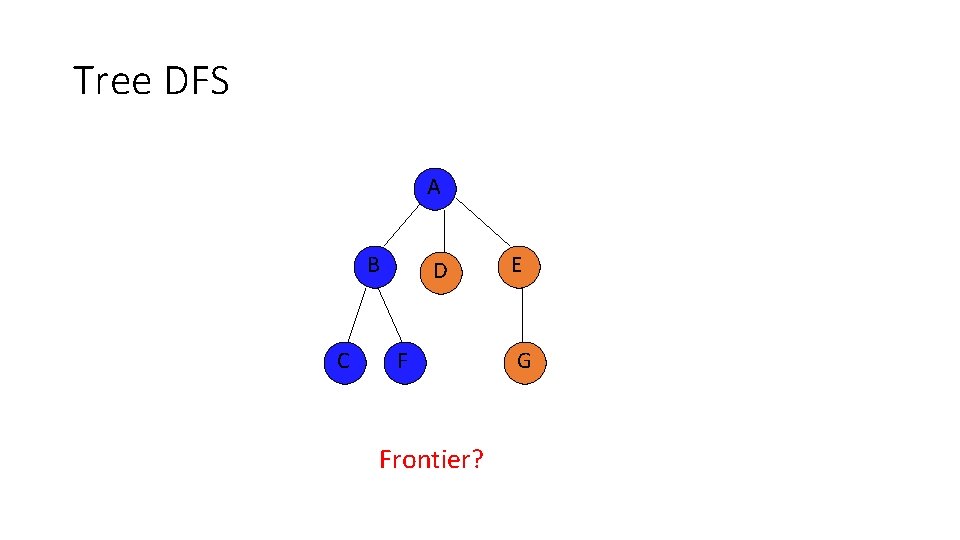
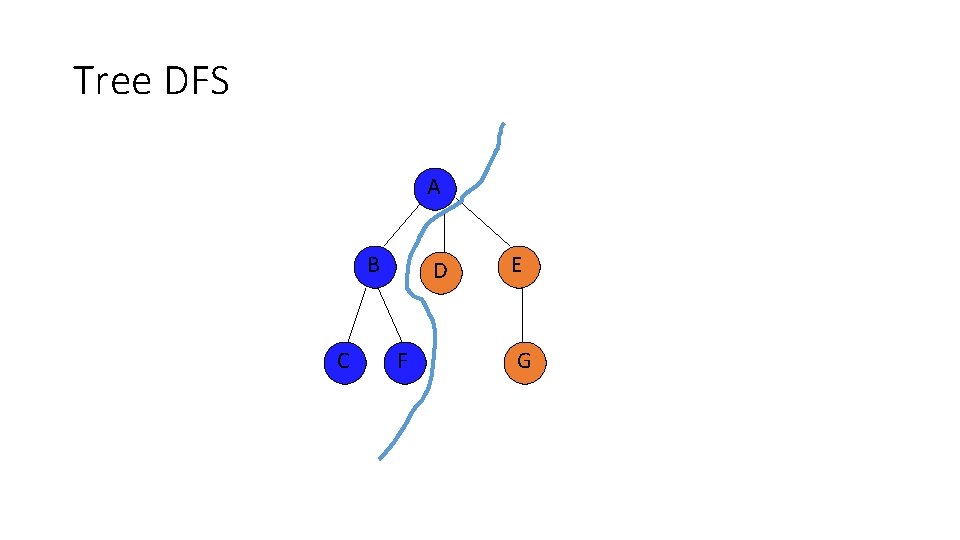
Tree DFS A B C D F Frontier? E G

Tree DFS A B C D F E G

Tree DFS A B C D F E G

Tree DFS A B C D F E G

Tree DFS A B C D F E G

DFS on graphs

DFS on graphs mark all nodes as not visited

DFS on graphs until all nodes have been visited repeatedly call DFSVisit

DFS on graphs What happened to the stack?

What does DFS do? • Finds connected components • Each call to DFS-Visit from DFS starts exploring a new set of connected components • Helps us understand the structure/connectedness of a graph

Running time? • Like BFS • Visits each node exactly once • Processes each edge exactly twice (for an undirected graph) • O(|V|+|E|)

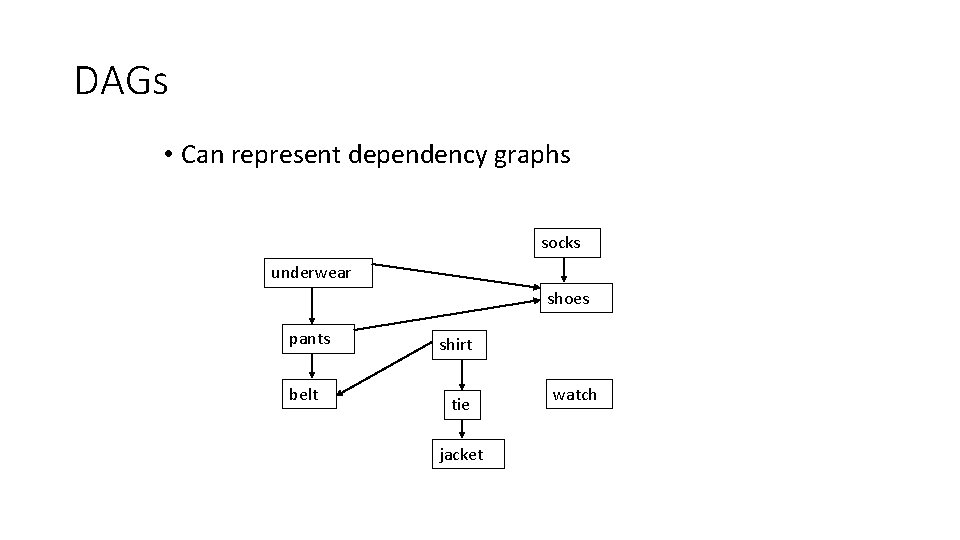
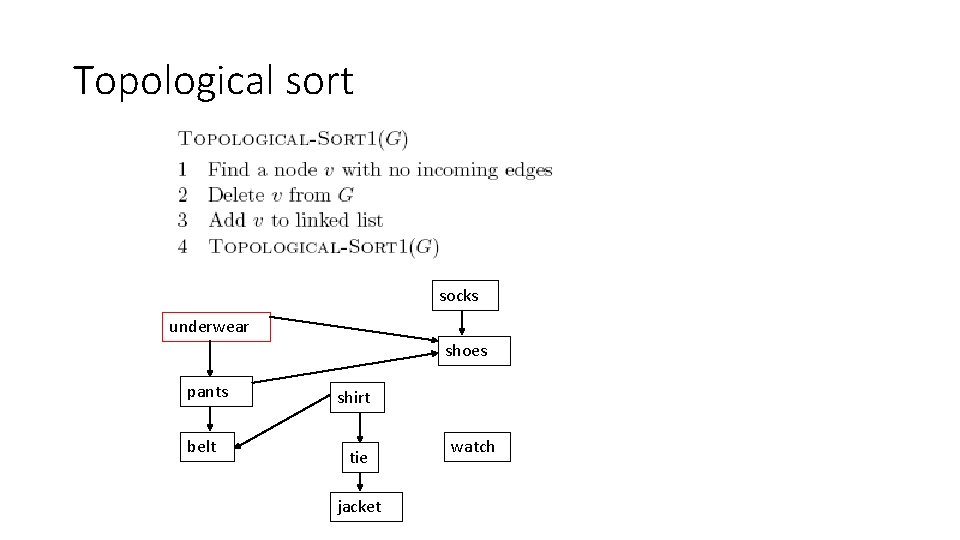
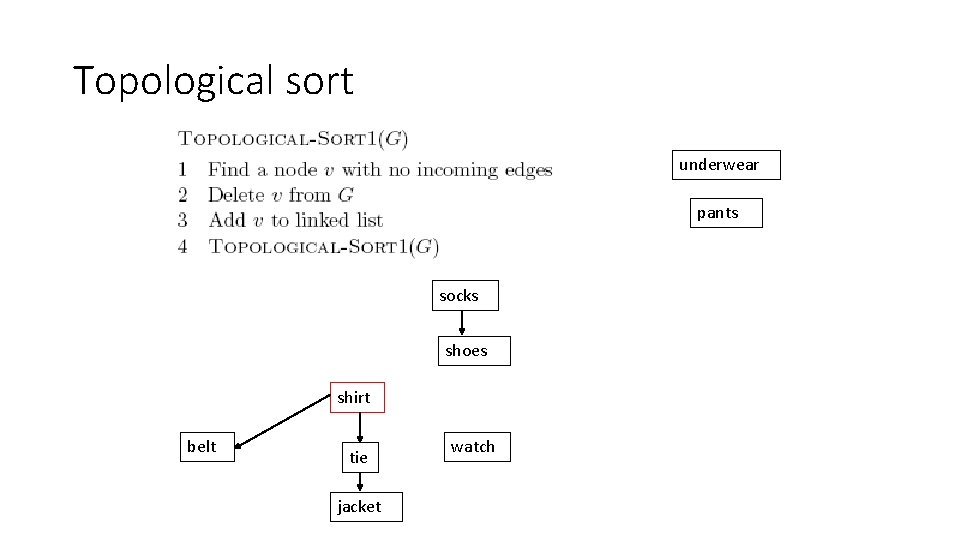
DAGs • Can represent dependency graphs socks underwear shoes pants belt shirt tie jacket watch

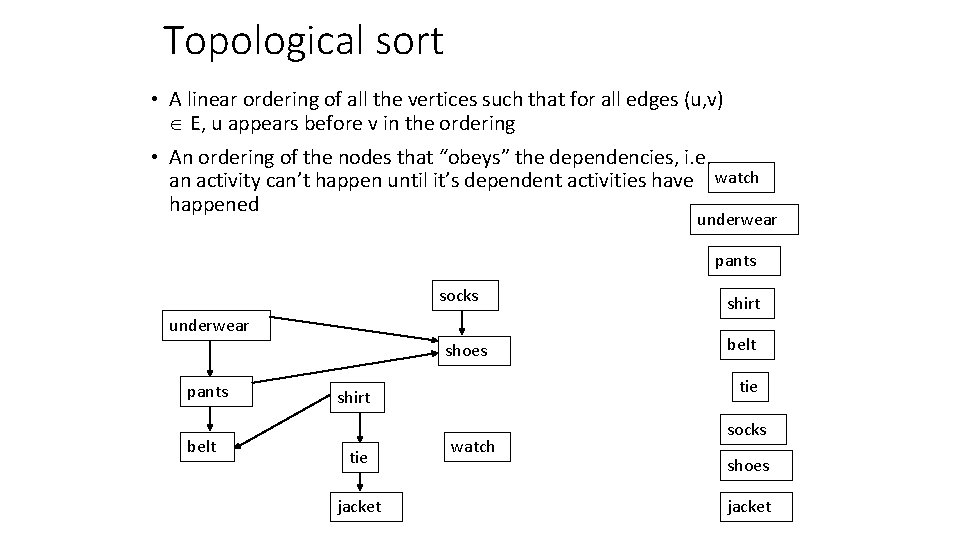
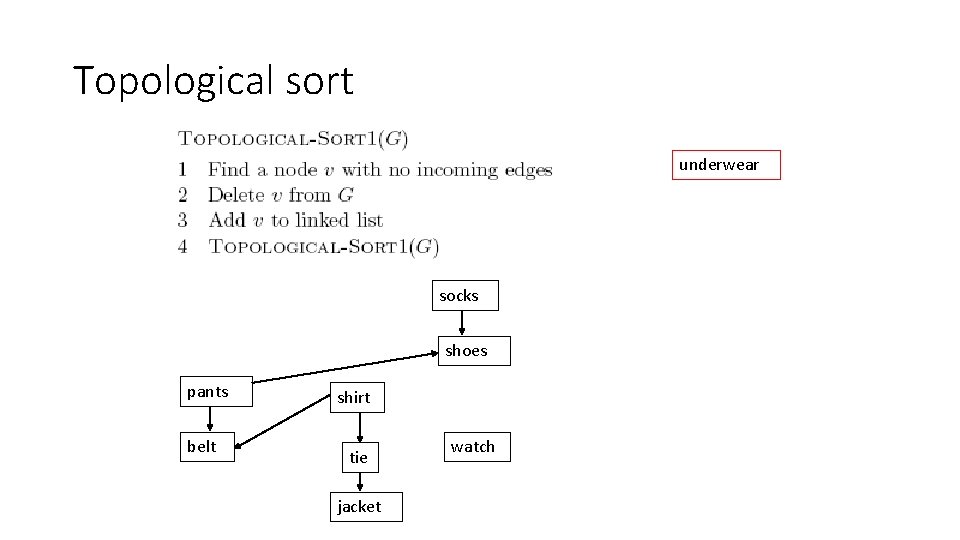
Topological sort • A linear ordering of all the vertices such that for all edges (u, v) E, u appears before v in the ordering • An ordering of the nodes that “obeys” the dependencies, i. e. an activity can’t happen until it’s dependent activities have watch happened underwear pants socks underwear shoes pants belt jacket belt tie shirt watch socks shoes jacket

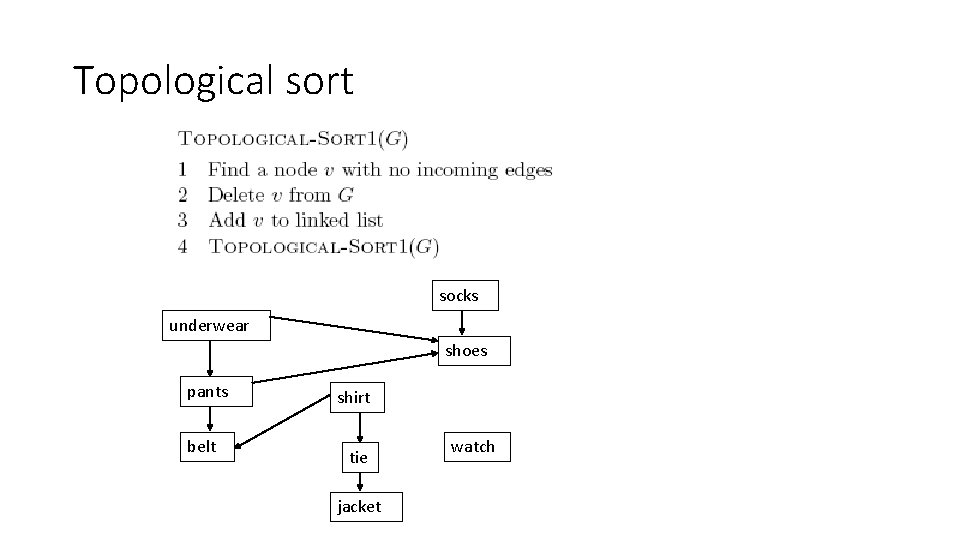
Topological sort

Topological sort socks underwear shoes pants belt shirt tie jacket watch

Topological sort socks underwear shoes pants belt shirt tie jacket watch

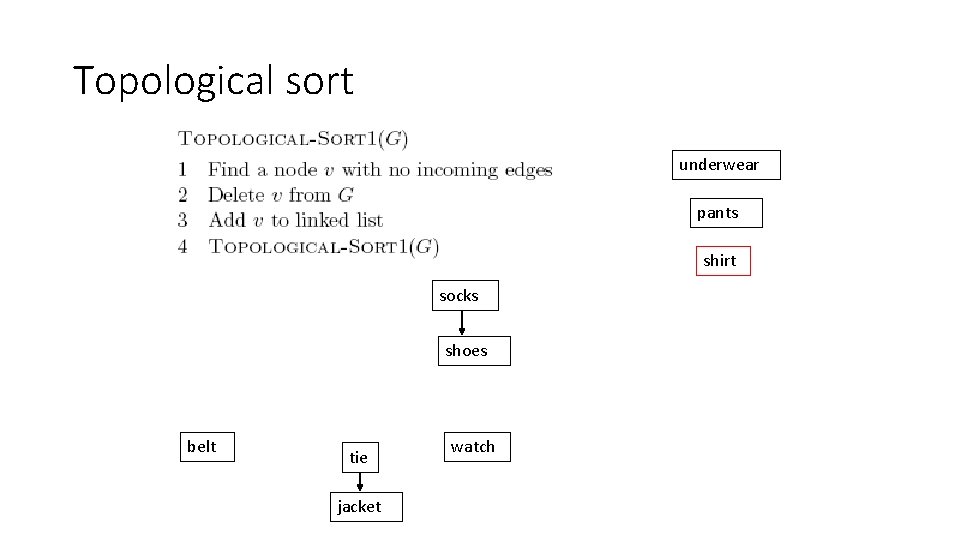
Topological sort underwear socks shoes pants belt shirt tie jacket watch

Topological sort underwear socks shoes pants belt shirt tie jacket watch

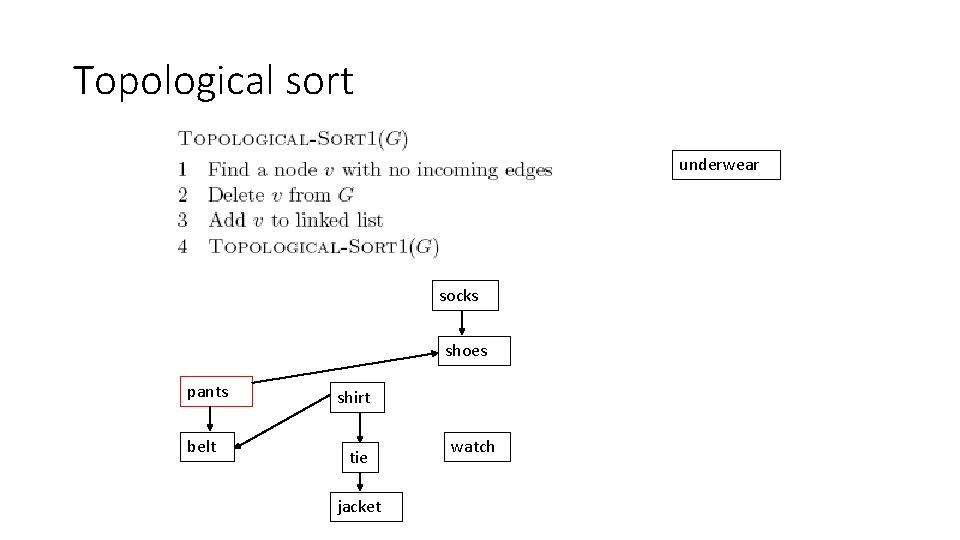
Topological sort underwear pants socks shoes shirt belt tie jacket watch

Topological sort underwear pants socks shoes shirt belt tie jacket watch

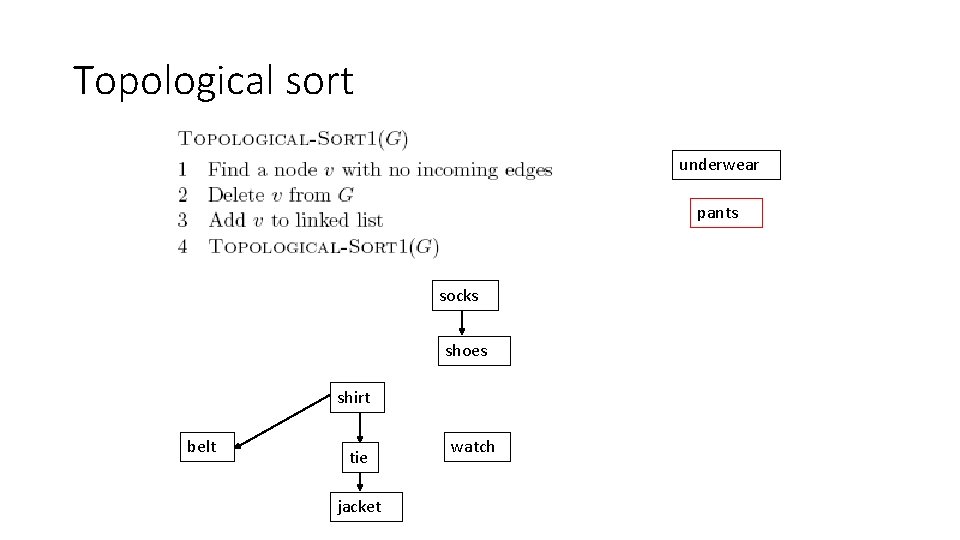
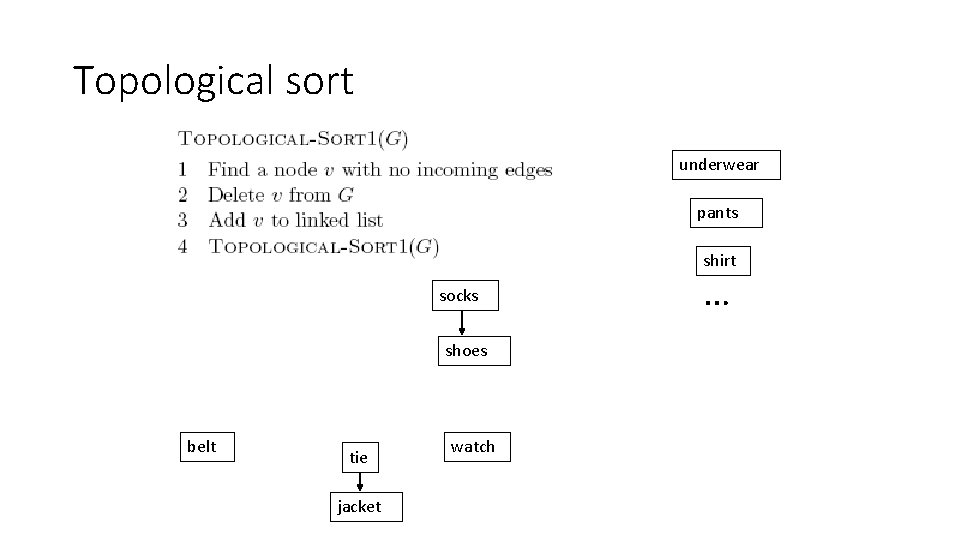
Topological sort underwear pants shirt socks shoes belt tie jacket watch

Topological sort underwear pants shirt socks shoes belt tie jacket watch …

Running time?

Running time? O(|V|+|E|)

Running time? O(E) overall

Running time? How many calls? |V|

Running time? Overall running time? O(|V|2+|V| |E|)

Can we do better?

Topological sort 2

Topological sort 2

Topological sort 2

Topological sort 2

Running time? • How many times do we process each node? • How many times do we process each edge? • O(|V| + |E|)

Strongly connected • Given a directed graph, can we reach any node v from any other node u? Ideas?

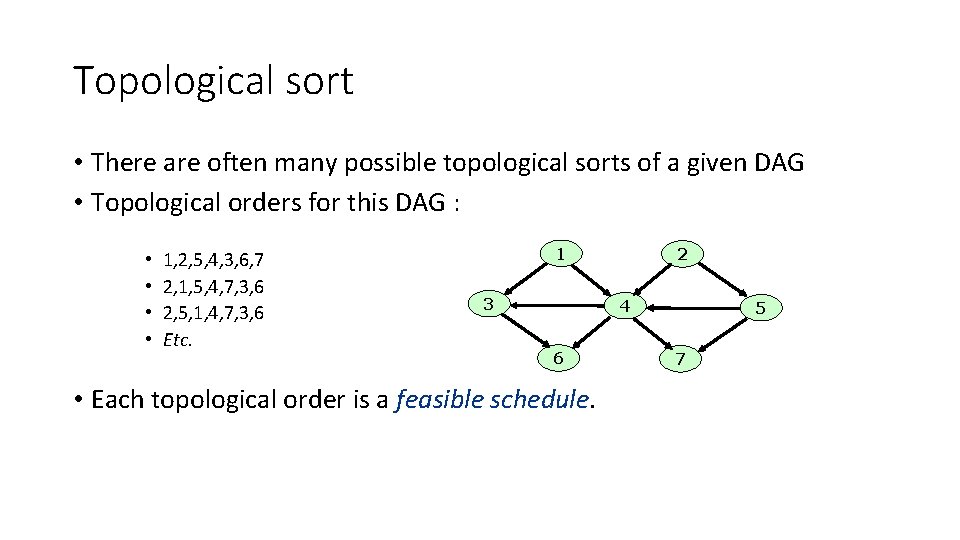
Topological sort • There are often many possible topological sorts of a given DAG • Topological orders for this DAG : • • 1, 2, 5, 4, 3, 6, 7 2, 1, 5, 4, 7, 3, 6 2, 5, 1, 4, 7, 3, 6 Etc. 1 3 2 4 6 • Each topological order is a feasible schedule. 5 7

Topological Sorts for Cyclic Graphs? Impossible! 1 2 3 • If v and w are two vertices on a cycle, there exist paths from v to w and from w to v. • Any ordering will contradict one of these paths

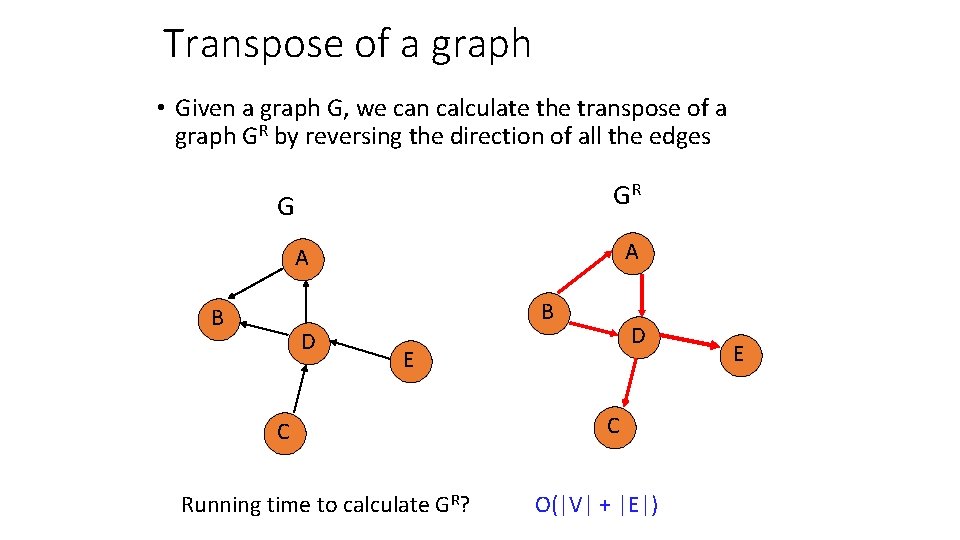
Transpose of a graph • Given a graph G, we can calculate the transpose of a graph GR by reversing the direction of all the edges GR G A A B B D D E C Running time to calculate GR? C O(|V| + |E|) E

Strongly connected

Runtime? O(|V| + |E|) O(|V|) O(|V| + |E|)

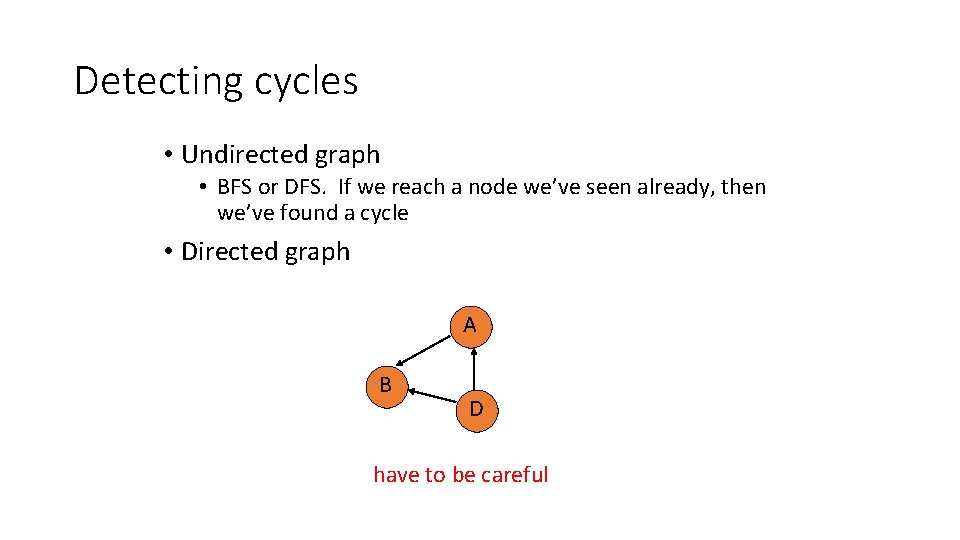
Detecting cycles • Undirected graph • BFS or DFS. If we reach a node we’ve seen already, then we’ve found a cycle • Directed graph A B D have to be careful

Detecting cycles • Undirected graph • BFS or DFS. • If we reach a node we’ve seen already, then we’ve found a cycle • Directed graph • Call Topological. Sort • If the length of the list returned ≠ |V| then a cycle exists

Problem: Laying Telephone Wire Central office

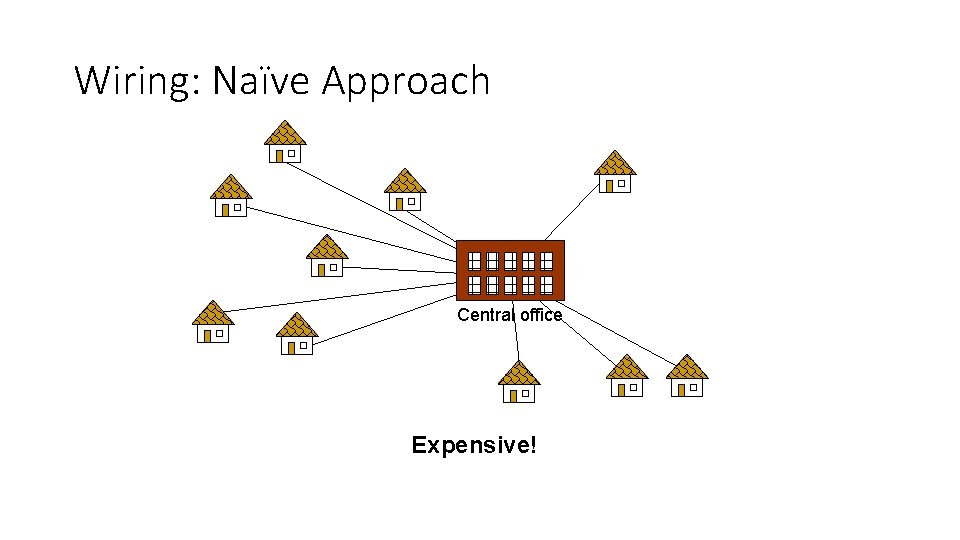
Wiring: Naïve Approach Central office Expensive!

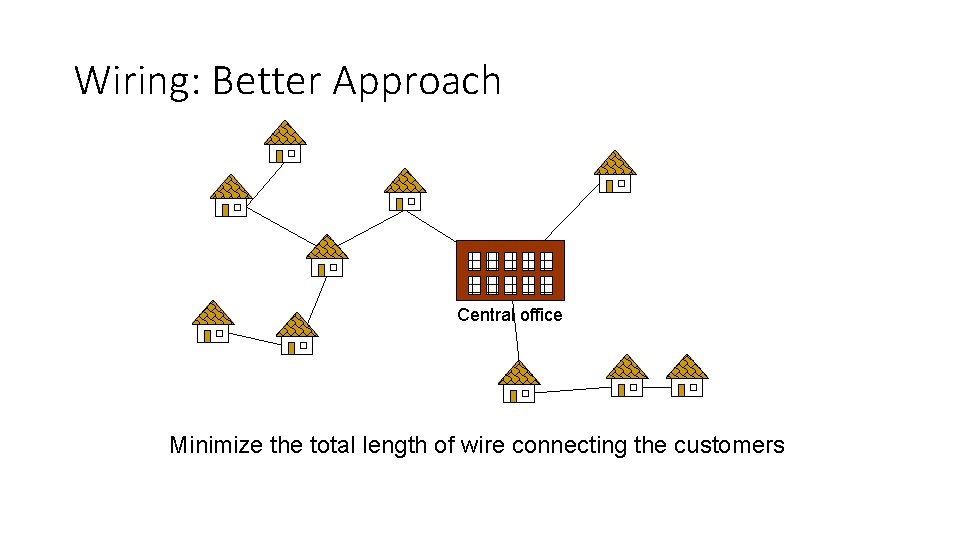
Wiring: Better Approach Central office Minimize the total length of wire connecting the customers

Minimum Spanning Tree (MST) A minimum spanning tree is a subgraph of an undirected weighted graph G, such that § it is a tree (i. e. , it is acyclic) § it covers all the vertices V Ø contains |V| - 1 edges § the total cost associated with tree edges is the minimum among all possible spanning trees § not necessarily unique

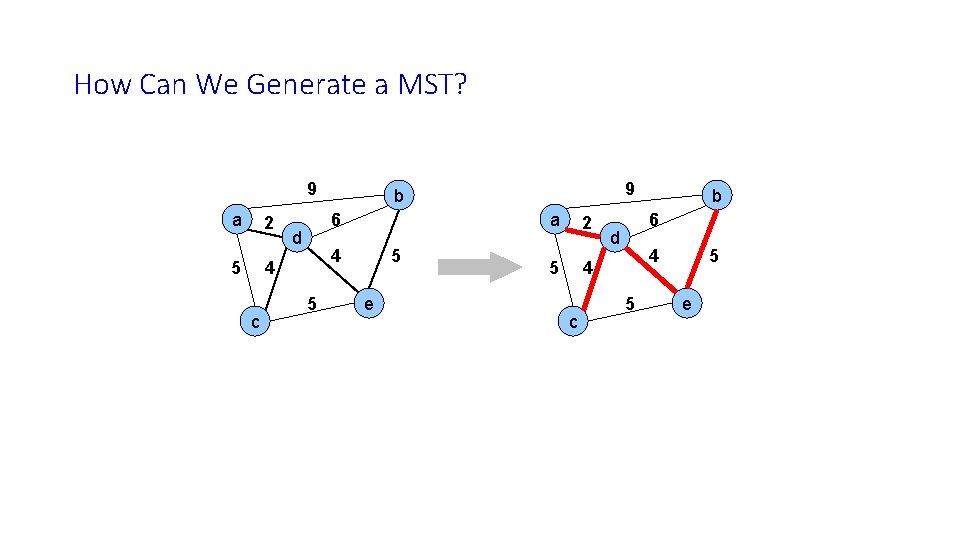
How Can We Generate a MST? 9 a 2 5 4 c 6 d 4 5 9 b 5 e a 2 5 4 c b 6 d 4 5 5 e

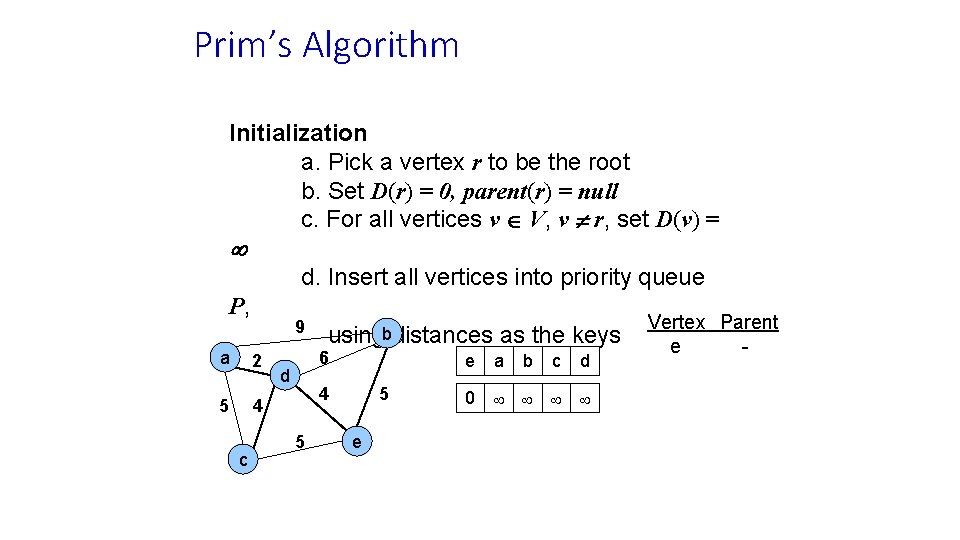
Prim’s Algorithm Initialization a. Pick a vertex r to be the root b. Set D(r) = 0, parent(r) = null c. For all vertices v V, v r, set D(v) = d. Insert all vertices into priority queue P, 9 a 2 5 4 c usingbdistances as the keys 6 d e 4 5 5 e a b c d 0 Vertex Parent e -

Prim’s Algorithm While P is not empty: //P is priority queue 1. Select the next vertex u to add to the tree u = P. delete. Min() 2. Update the weight of each vertex w adjacent to u which is not in the tree (i. e. , w P) If weight(u, w) < D(w), a. parent(w) = u b. D(w) = weight(u, w) c. Update the priority queue to reflect new distance for w

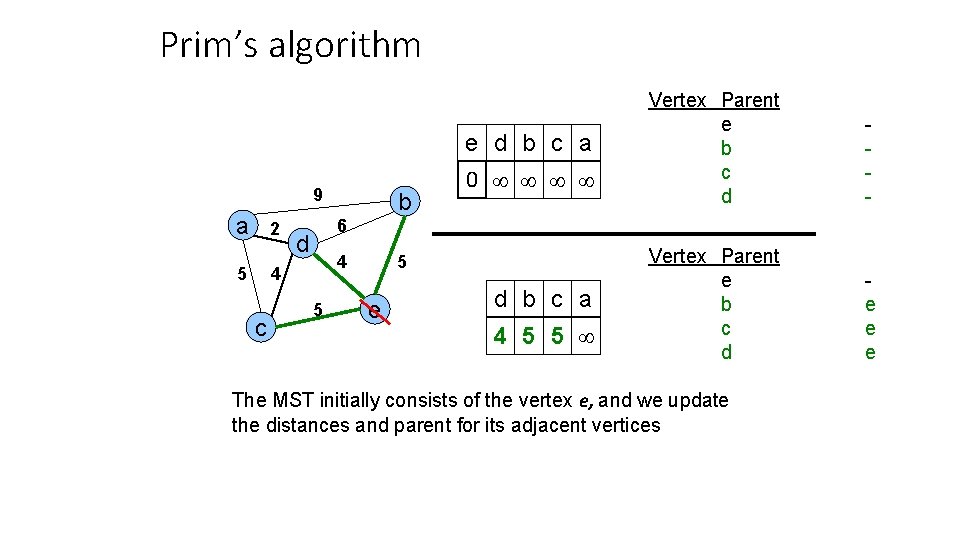
Prim’s algorithm e d b c a 9 a 2 5 - Vertex Parent e b c d e e e 6 d 4 4 c b 0 Vertex Parent e b c d 5 5 e d b c a 4 5 5 The MST initially consists of the vertex e, and we update the distances and parent for its adjacent vertices

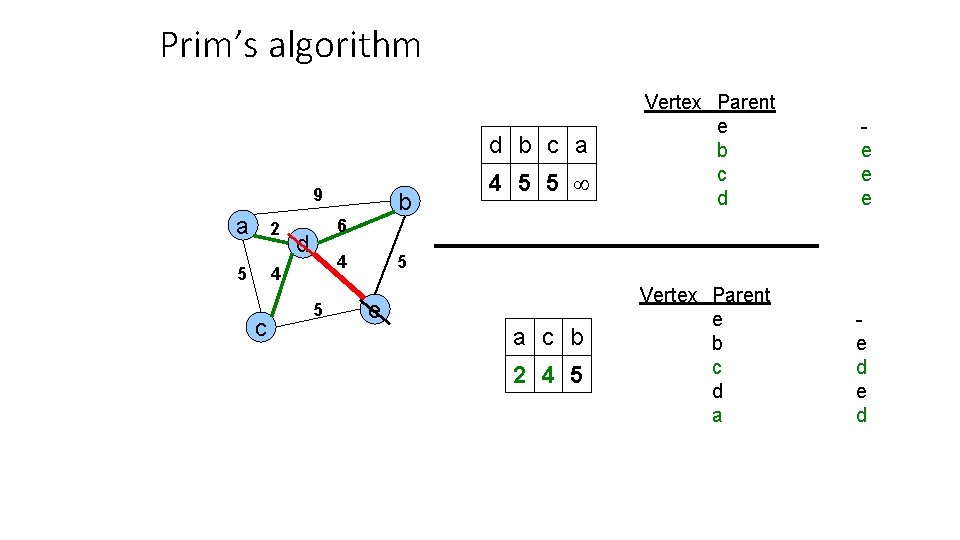
Prim’s algorithm d b c a 9 a 2 5 4 c b 4 5 5 Vertex Parent e b c d e e e Vertex Parent e b c d a e d 6 d 4 5 5 e a c b 2 4 5

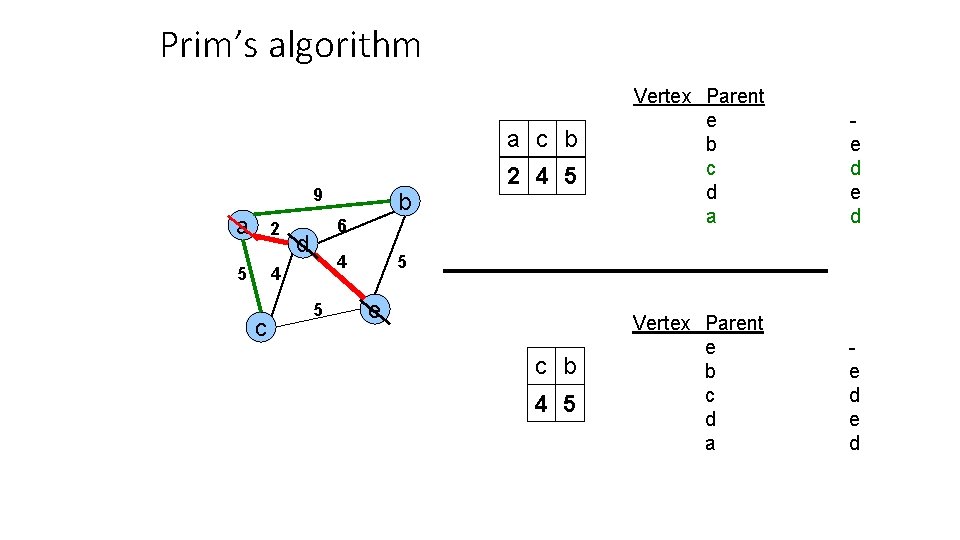
Prim’s algorithm a c b 9 a 2 5 4 c b 2 4 5 6 d 4 5 Vertex Parent e b c d a e d e d 5 e c b 4 5

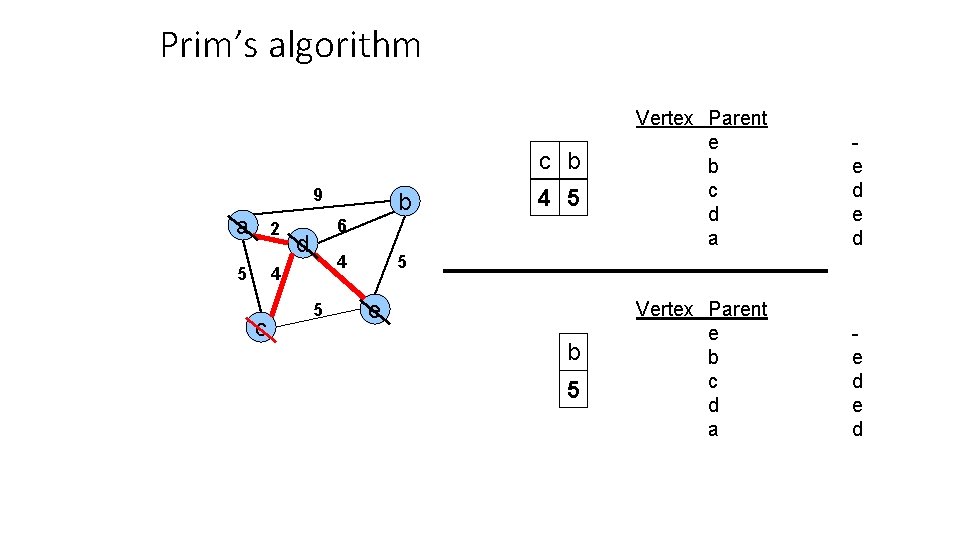
Prim’s algorithm c b 9 a 2 5 4 c b 4 5 6 d 4 5 Vertex Parent e b c d a e d e d 5 e b 5

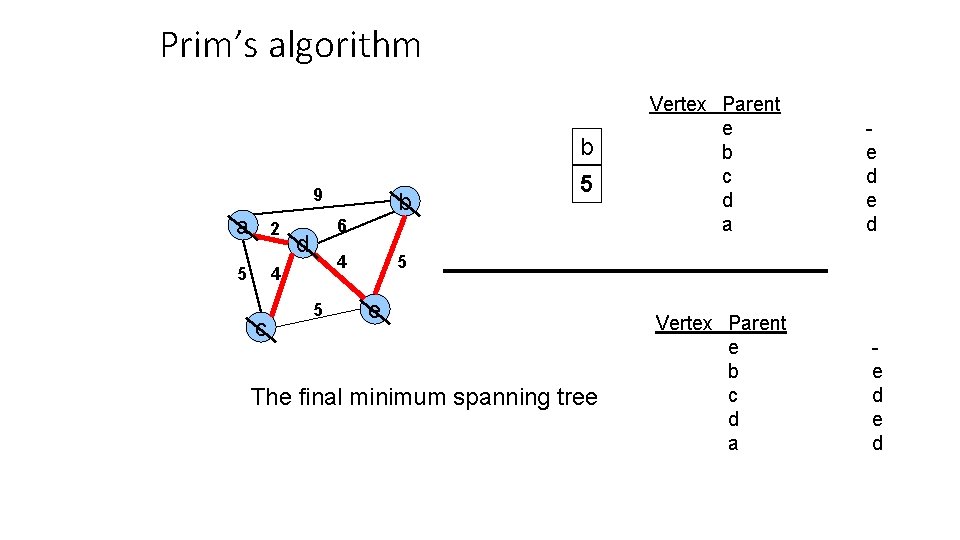
Prim’s algorithm b 9 a 2 5 4 c b 5 6 d 4 5 Vertex Parent e b c d a e d 5 e The final minimum spanning tree Vertex Parent e b c d a e d

Running time of Prim’s algorithm (without heaps) Initialization of priority queue (array): O(|V|) Update loop: |V| calls • Choosing vertex with minimum cost edge: O(|V|) • Updating distance values of unconnected vertices: each edge is considered only once during entire execution, for a total of O(|E|) updates 2)) O(|E| + |V| Overall cost without heaps: • What is the run time complexity if heaps are used?