Graphs Graphs Data structures that connect a set



![Graph Representation: Adjacency Matrix Adjacency matrix. V-by-V matrix (A) n A[i, j] = 1 Graph Representation: Adjacency Matrix Adjacency matrix. V-by-V matrix (A) n A[i, j] = 1](https://slidetodoc.com/presentation_image/008cc745c476e2ea27d5dcf2f99241ef/image-12.jpg)



- Slides: 48

Graphs

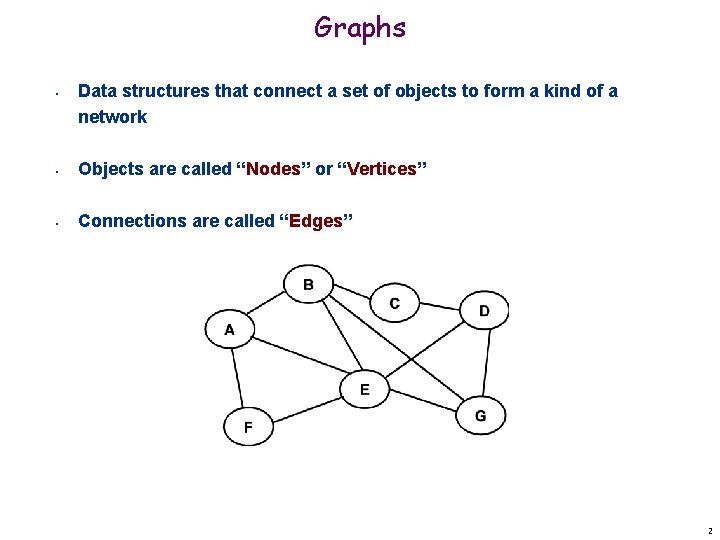
Graphs • Data structures that connect a set of objects to form a kind of a network • Objects are called “Nodes” or “Vertices” • Connections are called “Edges” 2

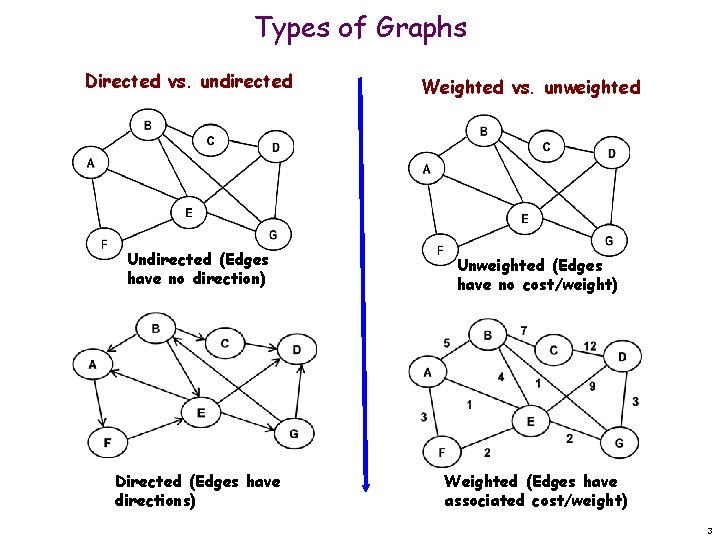
Types of Graphs Directed vs. undirected Weighted vs. unweighted Undirected (Edges have no direction) Unweighted (Edges have no cost/weight) Directed (Edges have directions) Weighted (Edges have associated cost/weight) 3

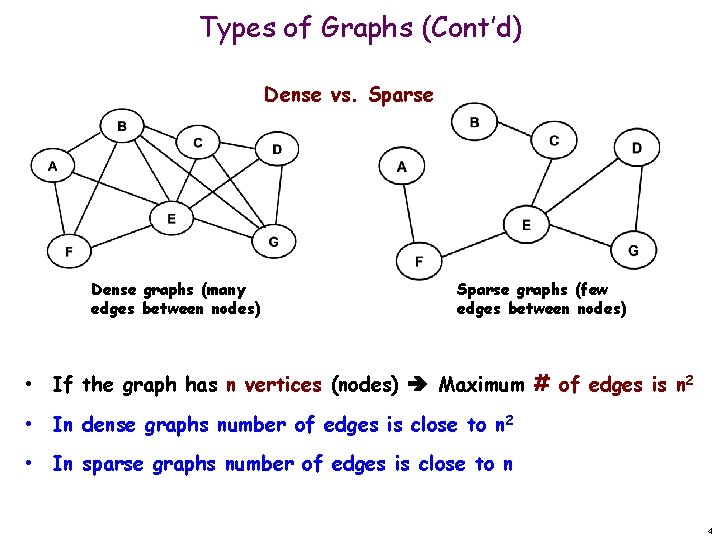
Types of Graphs (Cont’d) Dense vs. Sparse Dense graphs (many edges between nodes) Sparse graphs (few edges between nodes) • If the graph has n vertices (nodes) Maximum # of edges is n 2 • In dense graphs number of edges is close to n 2 • In sparse graphs number of edges is close to n 4

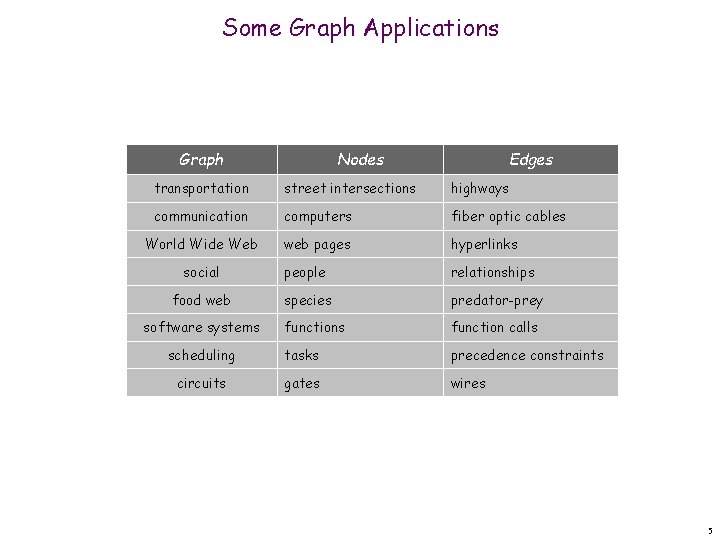
Some Graph Applications Graph Nodes Edges transportation street intersections highways communication computers fiber optic cables World Wide Web web pages hyperlinks social people relationships food web species predator-prey functions function calls scheduling tasks precedence constraints circuits gates wires software systems 5

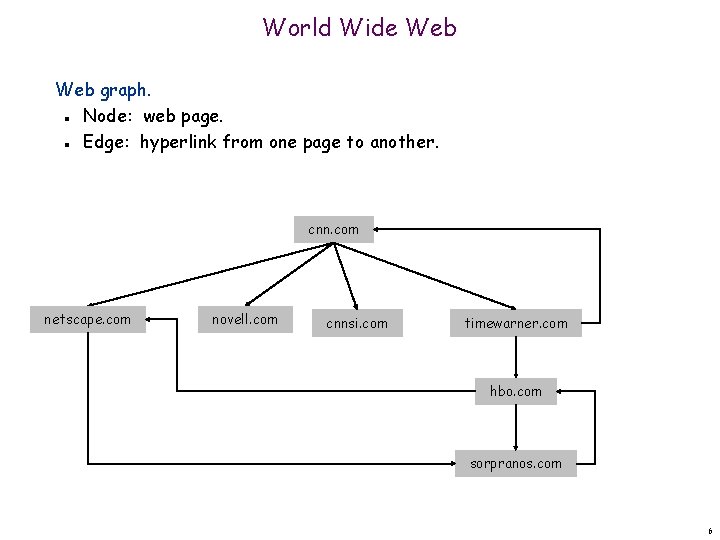
World Wide Web graph. Node: web page. Edge: hyperlink from one page to another. n n cnn. com netscape. com novell. com cnnsi. com timewarner. com hbo. com sorpranos. com 6

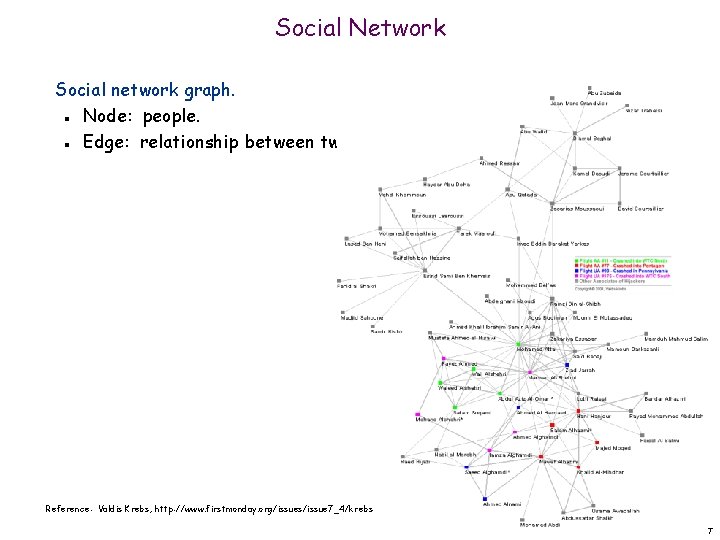
Social Network Social network graph. Node: people. Edge: relationship between two people. n n Reference: Valdis Krebs, http: //www. firstmonday. org/issues/issue 7_4/krebs 7

Protein Networks Nodes are proteins Edges are connections (interaction between proteins) 8

More Formalization 9

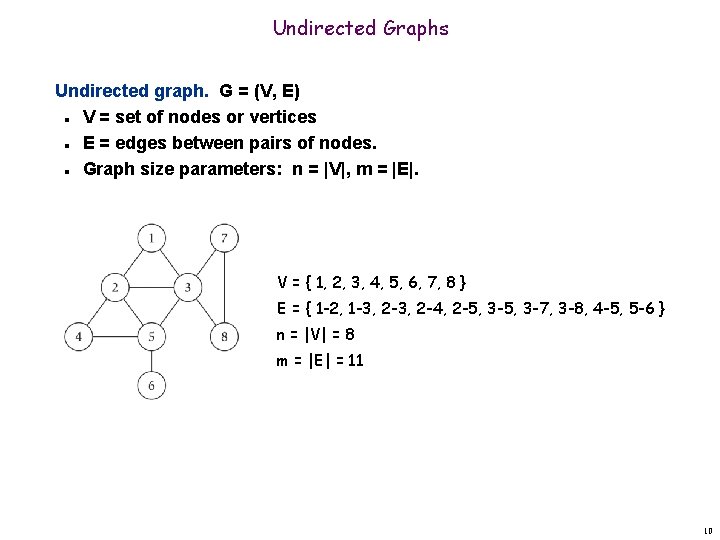
Undirected Graphs Undirected graph. G = (V, E) V = set of nodes or vertices E = edges between pairs of nodes. Graph size parameters: n = |V|, m = |E|. n n n V = { 1, 2, 3, 4, 5, 6, 7, 8 } E = { 1 -2, 1 -3, 2 -4, 2 -5, 3 -7, 3 -8, 4 -5, 5 -6 } n = |V| = 8 m = |E| = 11 10

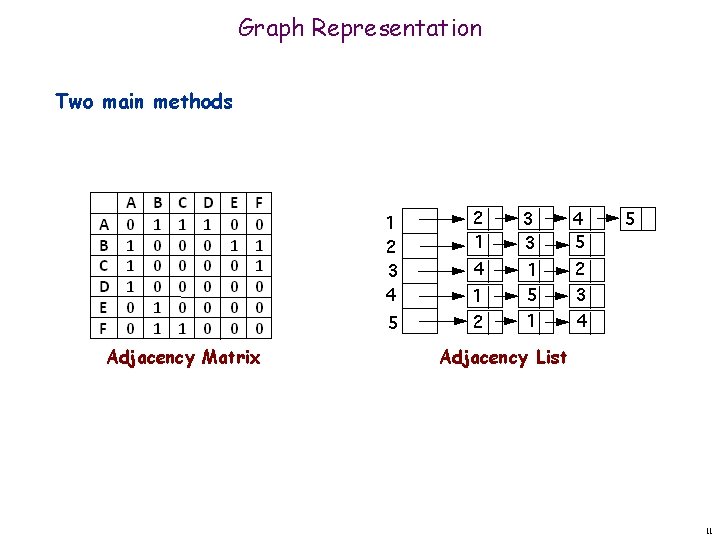
Graph Representation Two main methods Adjacency Matrix Adjacency List 11
![Graph Representation Adjacency Matrix Adjacency matrix VbyV matrix A n Ai j 1 Graph Representation: Adjacency Matrix Adjacency matrix. V-by-V matrix (A) n A[i, j] = 1](https://slidetodoc.com/presentation_image/008cc745c476e2ea27d5dcf2f99241ef/image-12.jpg)
Graph Representation: Adjacency Matrix Adjacency matrix. V-by-V matrix (A) n A[i, j] = 1 if exists edge between node i and node j n Space proportional to V 2 n Checking if (u, v) is an edge takes (1) time. n Identifying all edges takes (V 2) time. n For undirected graph matrix is symmetric across the diagonal Vertices 1 2 3 4 5 6 7 8 1 0 1 1 0 0 0 2 1 0 1 1 1 0 0 0 3 1 1 0 0 1 1 4 0 1 1 0 0 0 5 0 1 1 1 0 0 6 0 0 1 0 0 0 7 0 0 1 8 0 0 1 0 12

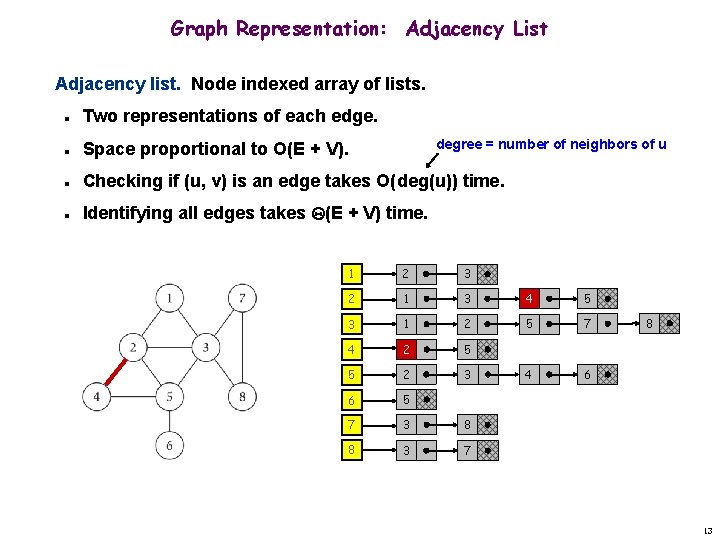
Graph Representation: Adjacency List Adjacency list. Node indexed array of lists. n Two representations of each edge. n Space proportional to O(E + V). n Checking if (u, v) is an edge takes O(deg(u)) time. n Identifying all edges takes (E + V) time. degree = number of neighbors of u 1 2 3 2 1 3 4 5 3 1 2 5 7 4 2 5 5 2 3 4 6 6 5 7 3 8 8 3 7 8 13

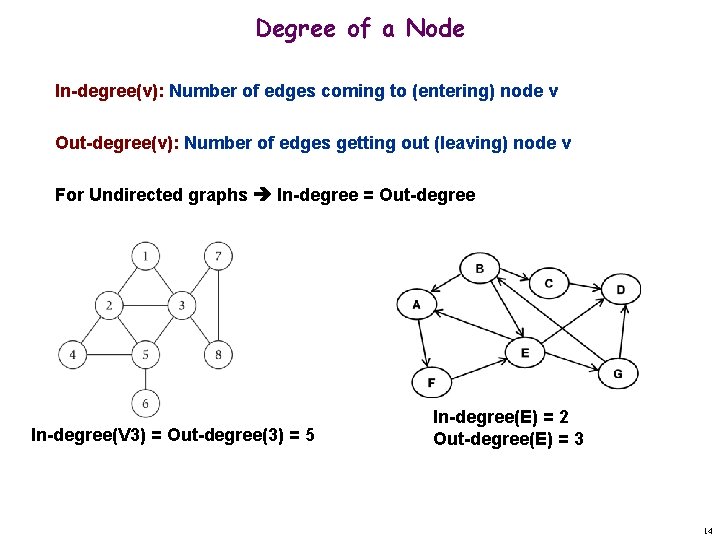
Degree of a Node In-degree(v): Number of edges coming to (entering) node v Out-degree(v): Number of edges getting out (leaving) node v For Undirected graphs In-degree = Out-degree In-degree(V 3) = Out-degree(3) = 5 In-degree(E) = 2 Out-degree(E) = 3 14

Graph Traversal 15

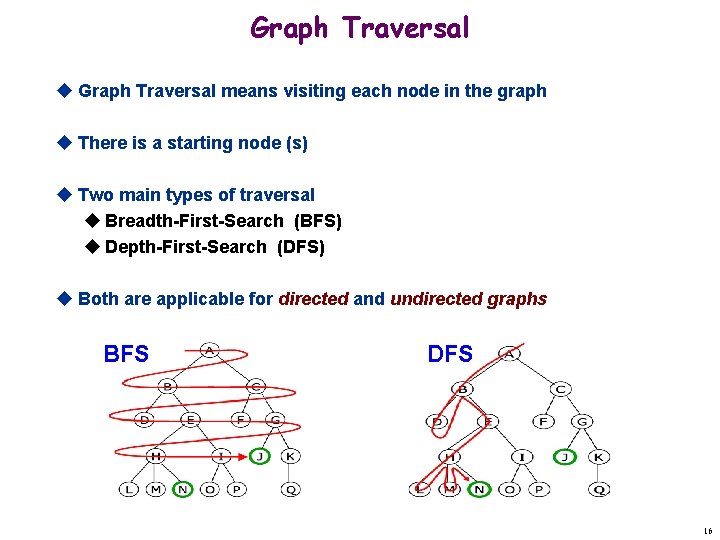
Graph Traversal u Graph Traversal means visiting each node in the graph u There is a starting node (s) u Two main types of traversal u Breadth-First-Search (BFS) u Depth-First-Search (DFS) u Both are applicable for directed and undirected graphs BFS DFS 16

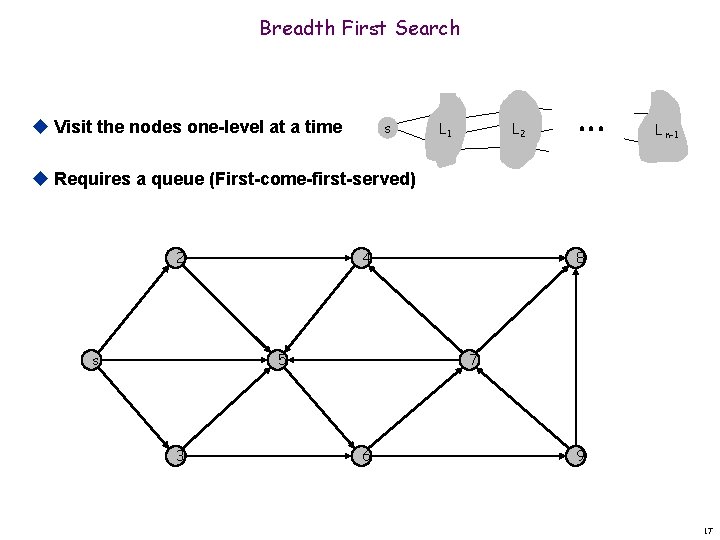
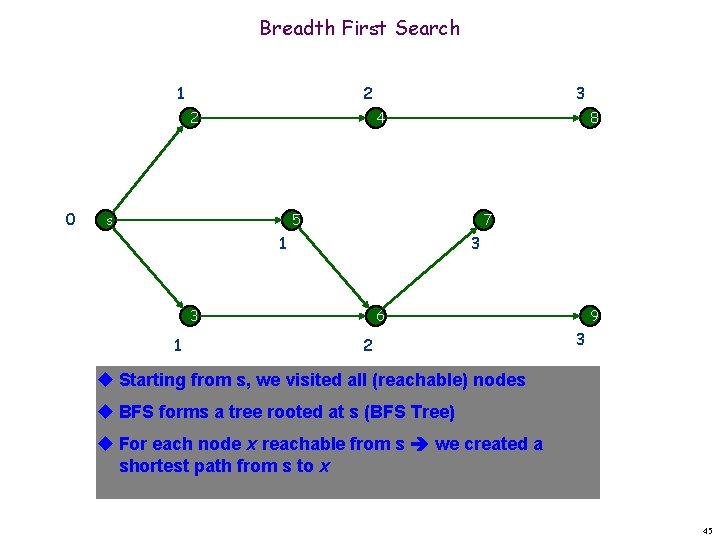
Breadth First Search u Visit the nodes one-level at a time s L 1 L 2 L n-1 u Requires a queue (First-come-first-served) 2 s 4 5 3 8 7 6 9 17

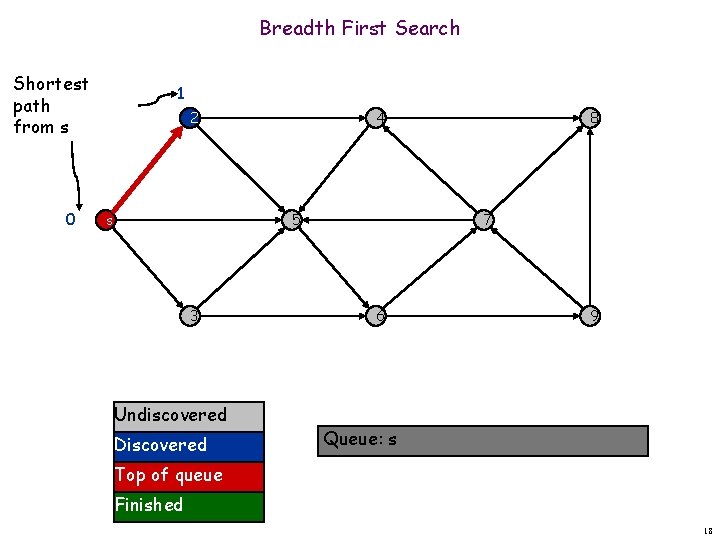
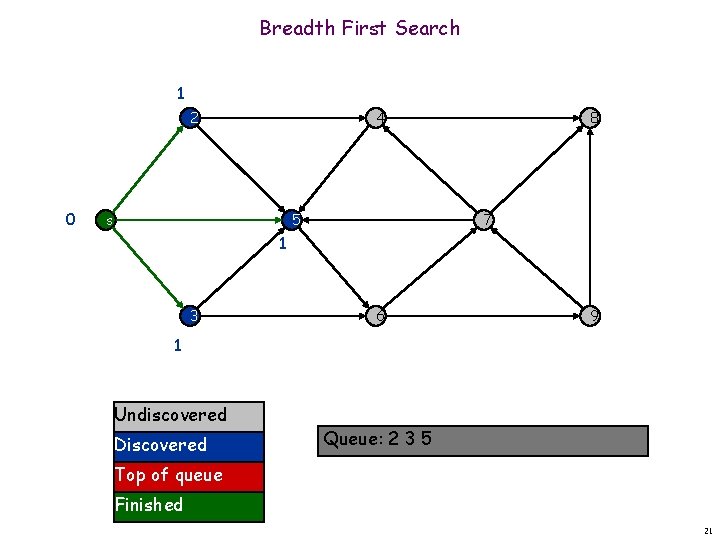
Breadth First Search Shortest path from s 0 1 2 s 4 5 3 Undiscovered Discovered 8 7 6 9 Queue: s Top of queue Finished 18

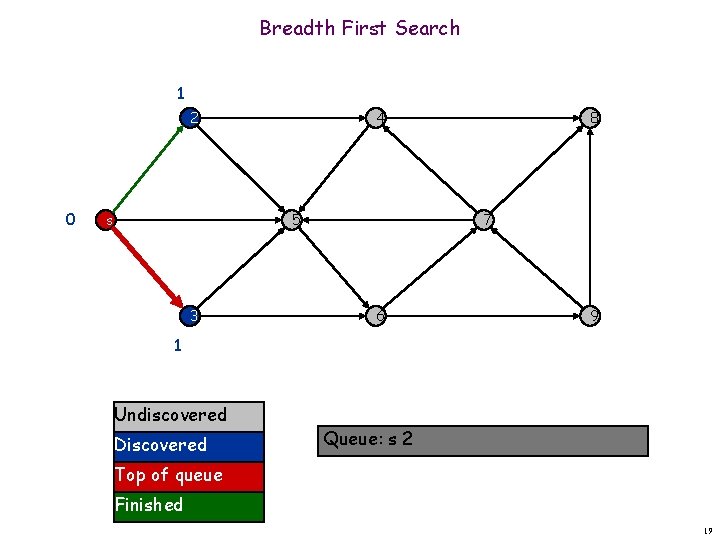
Breadth First Search 1 2 0 s 4 5 3 8 7 6 9 1 Undiscovered Discovered Queue: s 2 Top of queue Finished 19

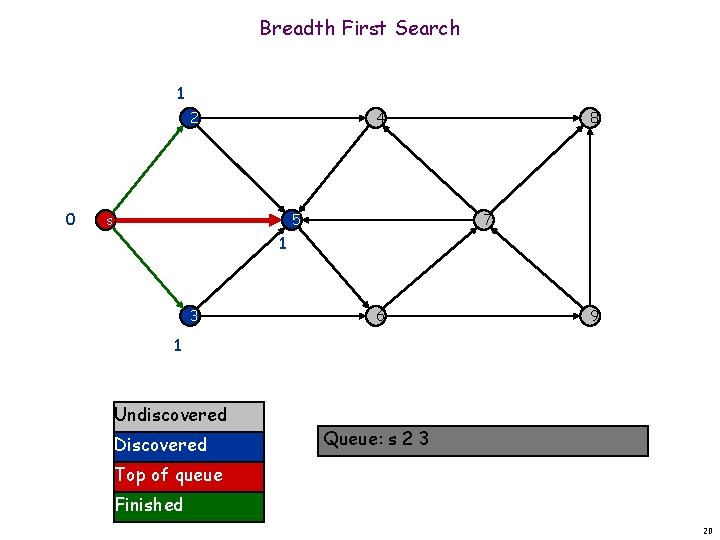
Breadth First Search 1 2 0 4 5 s 8 7 1 3 6 9 1 Undiscovered Discovered Queue: s 2 3 Top of queue Finished 20

Breadth First Search 1 2 0 4 s 5 8 7 1 3 6 9 1 Undiscovered Discovered Queue: 2 3 5 Top of queue Finished 21

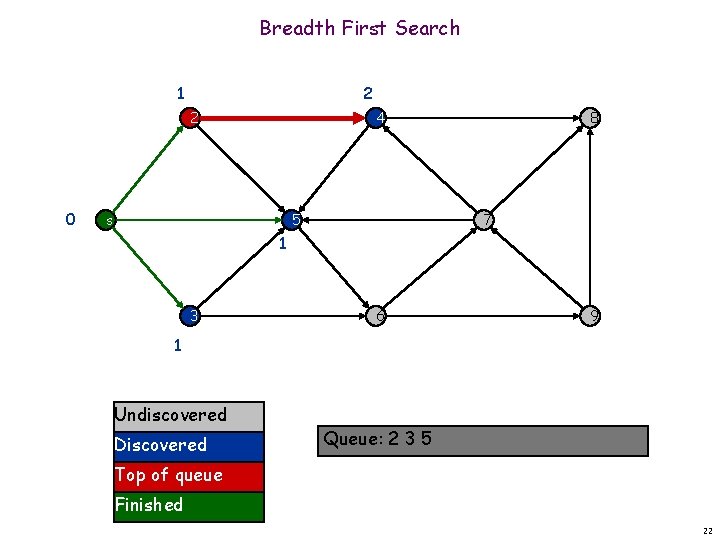
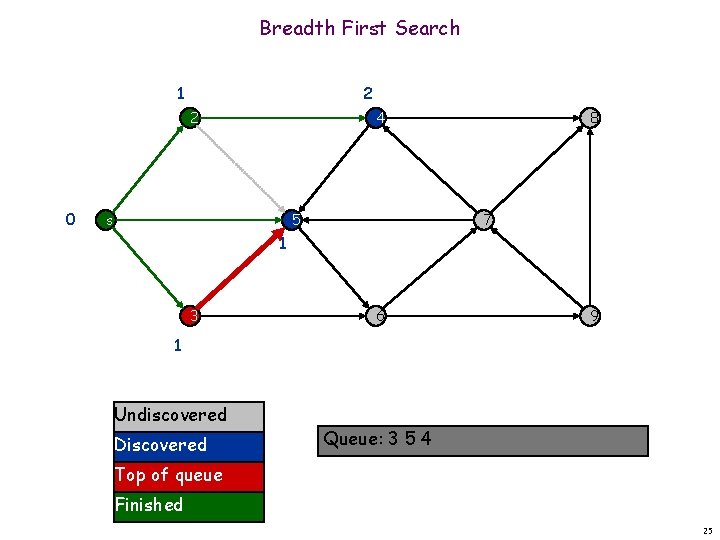
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 9 1 Undiscovered Discovered Queue: 2 3 5 Top of queue Finished 22

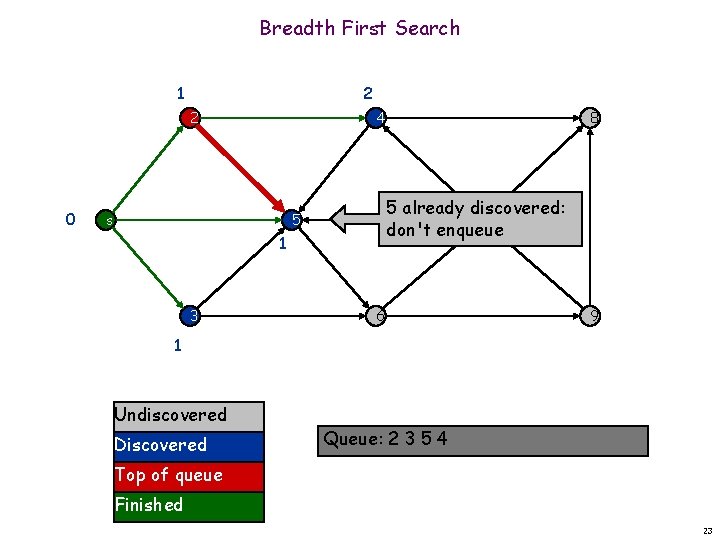
Breadth First Search 1 2 2 0 4 s 5 already discovered: 7 don't enqueue 5 1 3 8 6 9 1 Undiscovered Discovered Queue: 2 3 5 4 Top of queue Finished 23

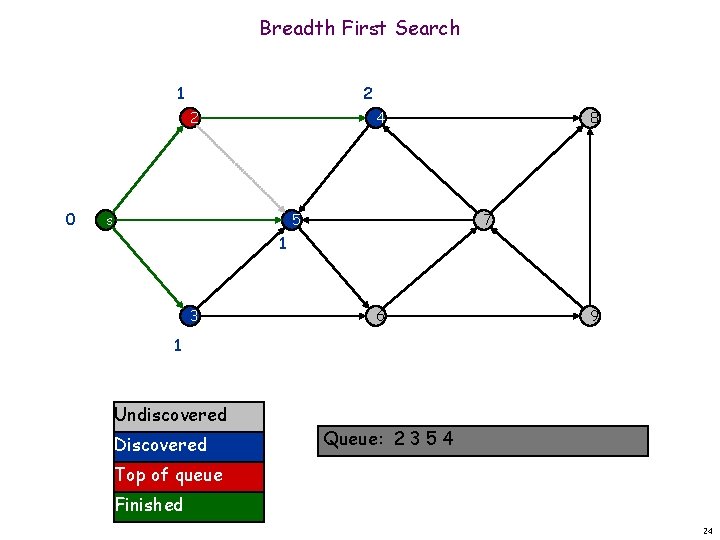
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 9 1 Undiscovered Discovered Queue: 2 3 5 4 Top of queue Finished 24

Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 9 1 Undiscovered Discovered Queue: 3 5 4 Top of queue Finished 25

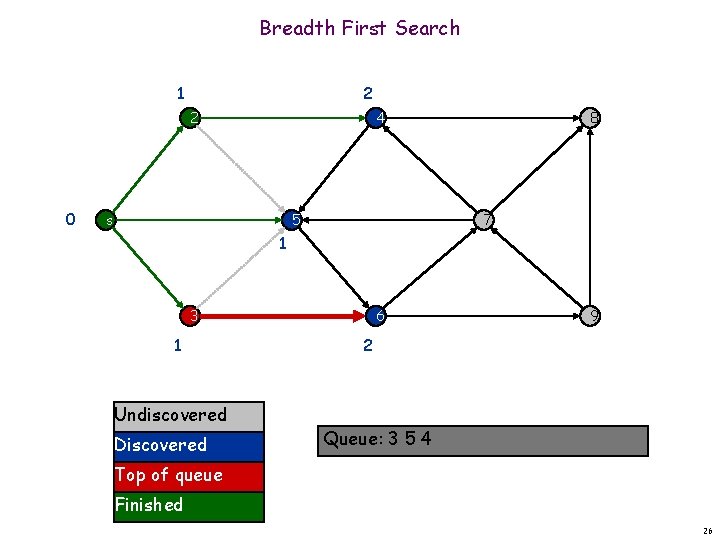
Breadth First Search 1 2 2 0 4 s 5 8 7 1 6 3 1 Undiscovered Discovered 9 2 Queue: 3 5 4 Top of queue Finished 26

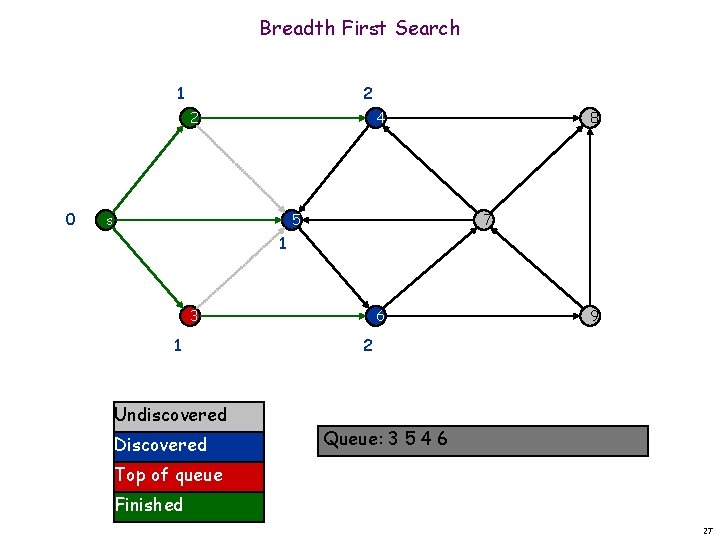
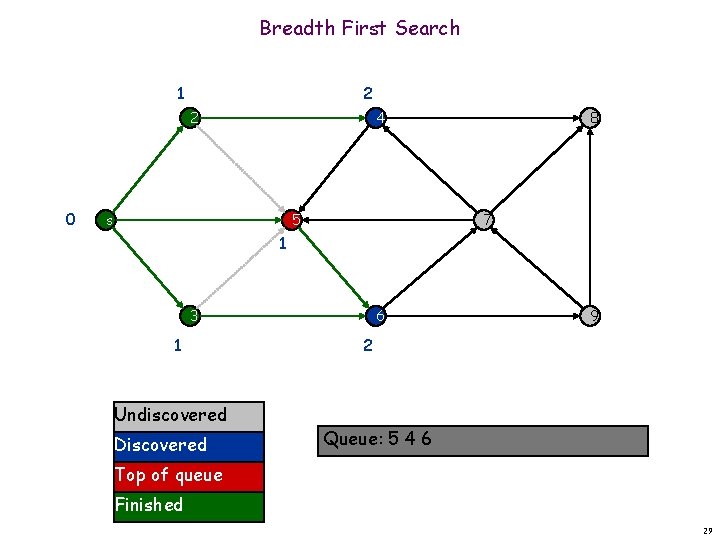
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 3 5 4 6 Top of queue Finished 27

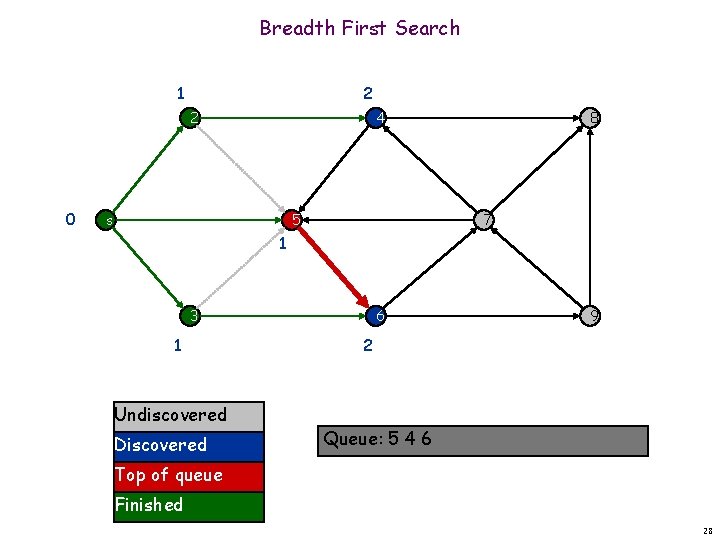
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 5 4 6 Top of queue Finished 28

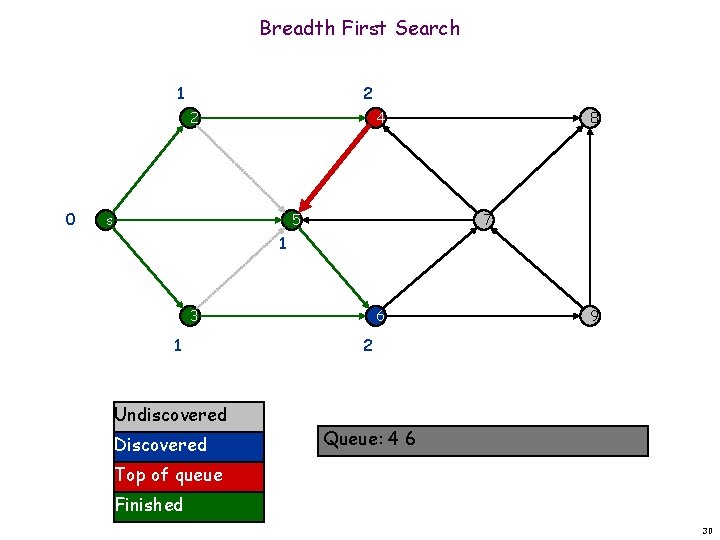
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 5 4 6 Top of queue Finished 29

Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 4 6 Top of queue Finished 30

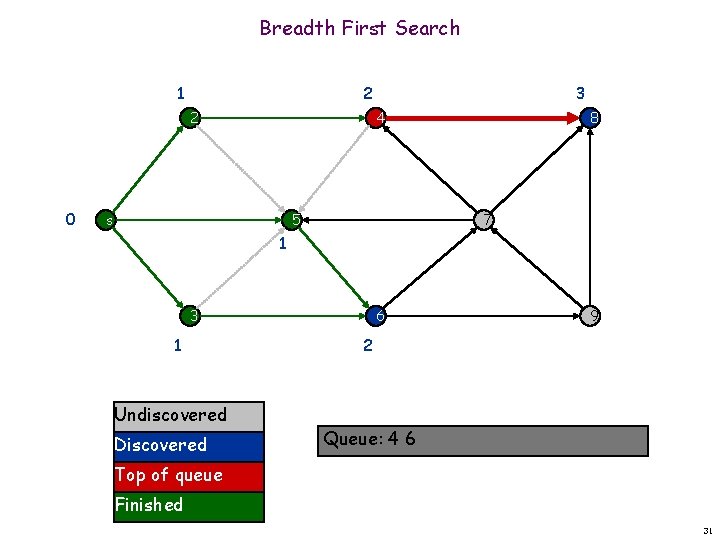
Breadth First Search 1 2 2 0 3 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 4 6 Top of queue Finished 31

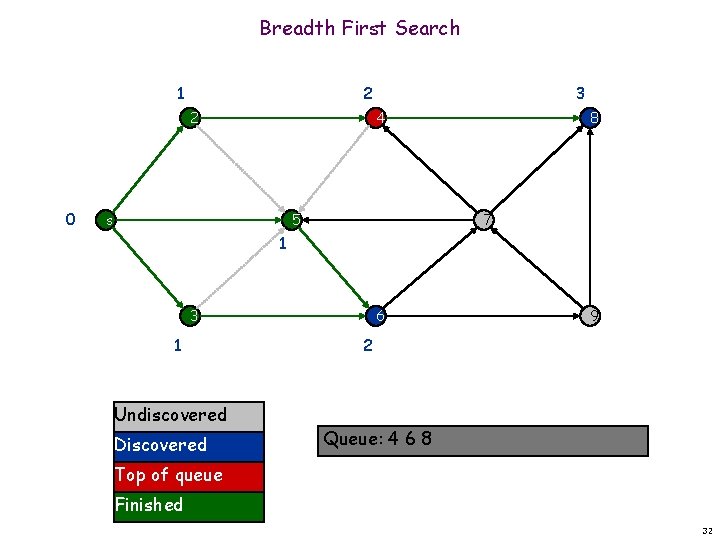
Breadth First Search 1 2 2 0 3 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 4 6 8 Top of queue Finished 32

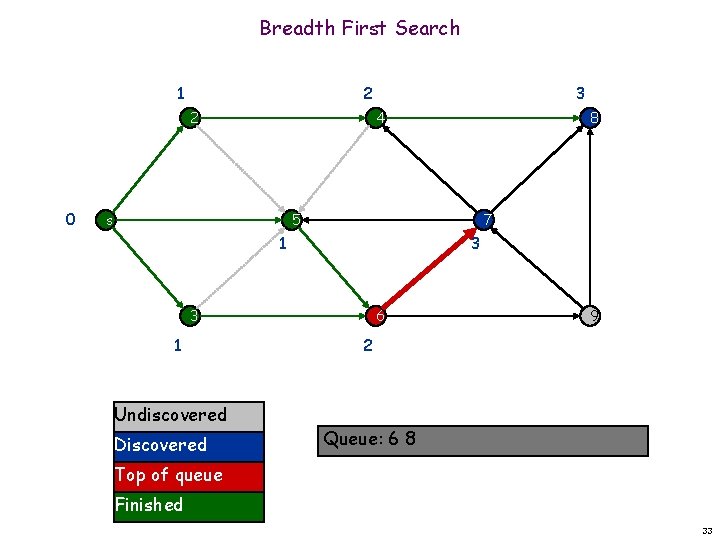
Breadth First Search 1 2 2 0 3 4 s 8 7 5 1 3 3 1 Undiscovered Discovered 6 9 2 Queue: 6 8 Top of queue Finished 33

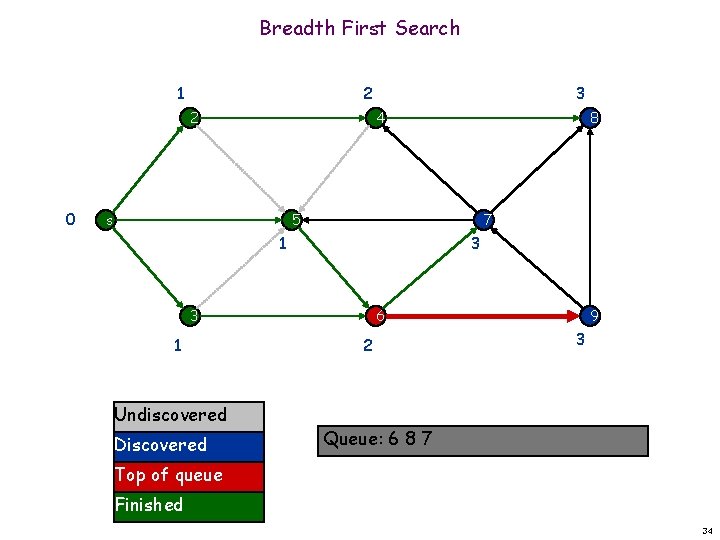
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 6 8 7 Top of queue Finished 34

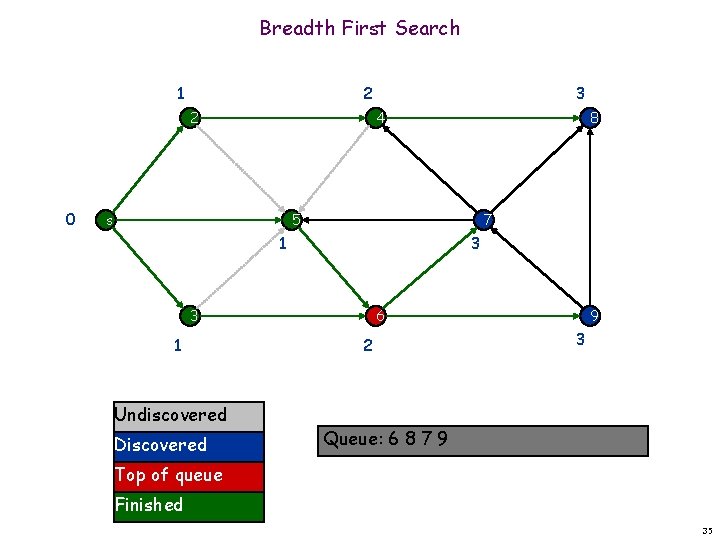
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 6 8 7 9 Top of queue Finished 35

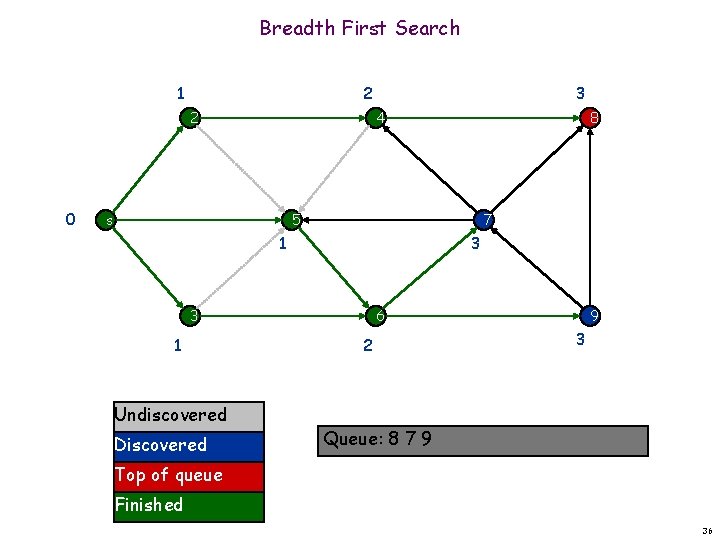
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 8 7 9 Top of queue Finished 36

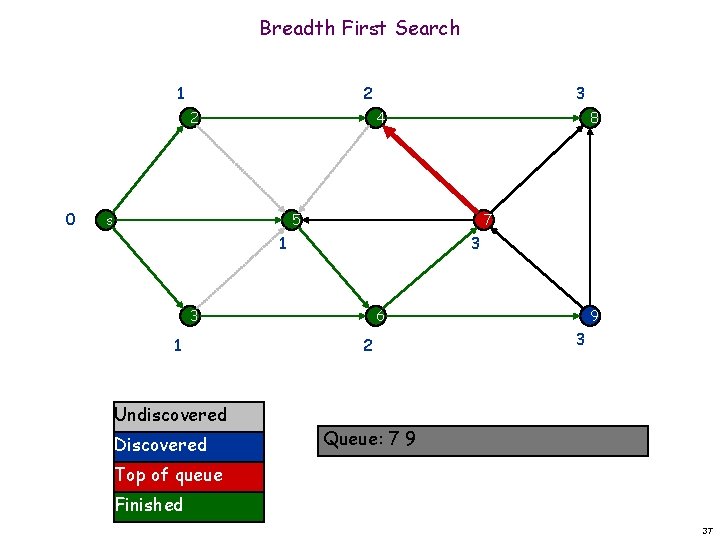
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 7 9 Top of queue Finished 37

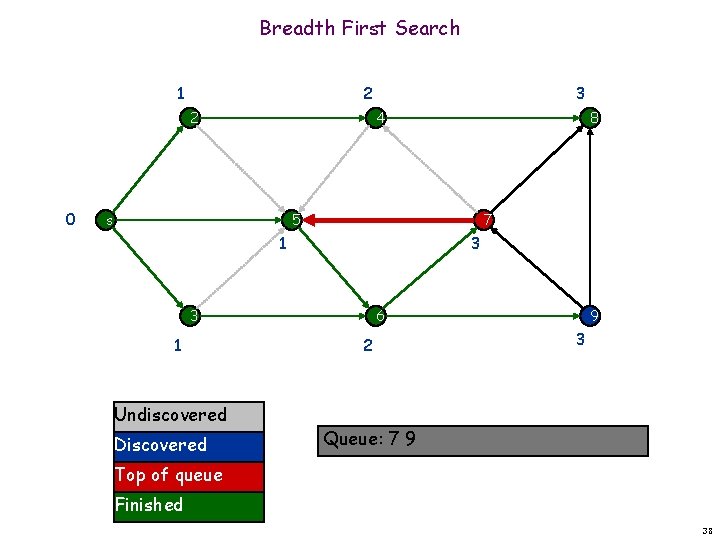
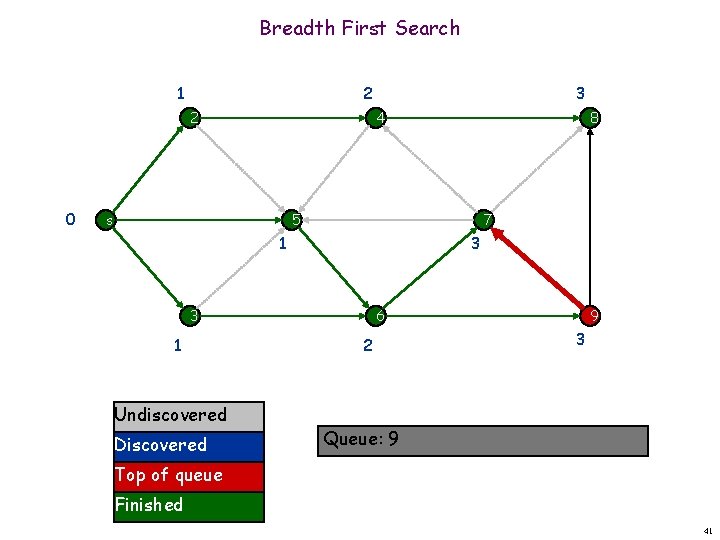
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 7 9 Top of queue Finished 38

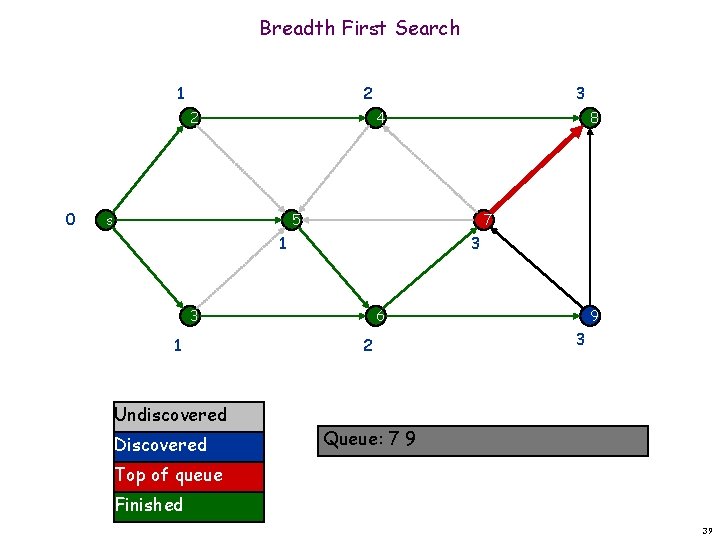
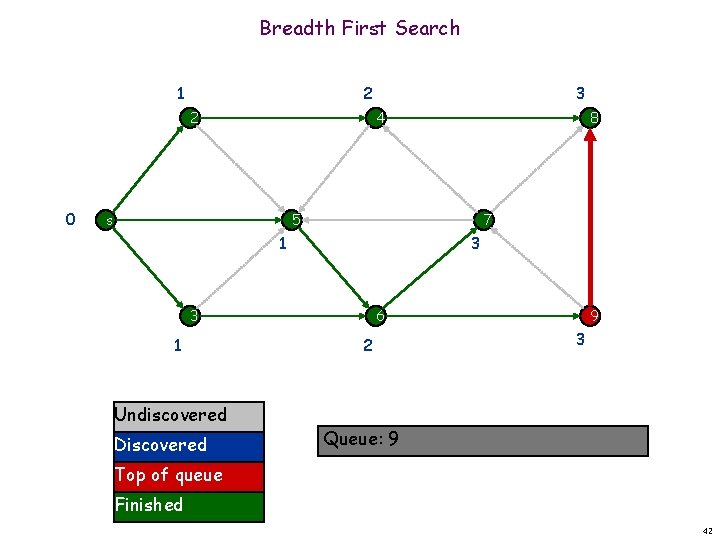
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 7 9 Top of queue Finished 39

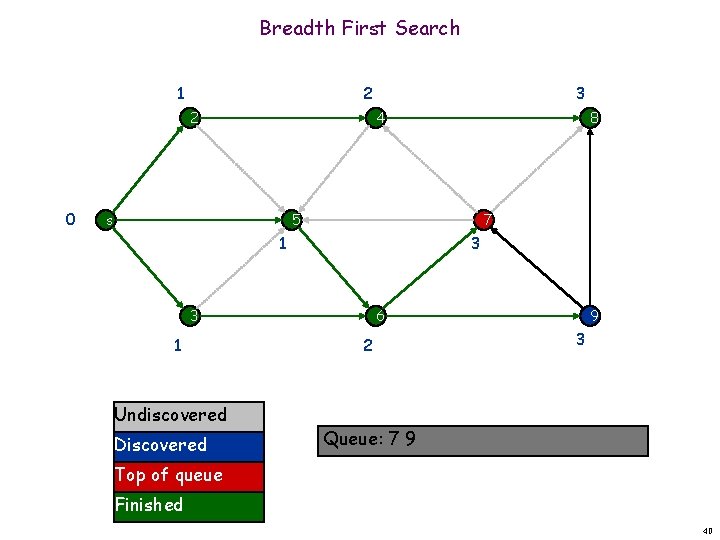
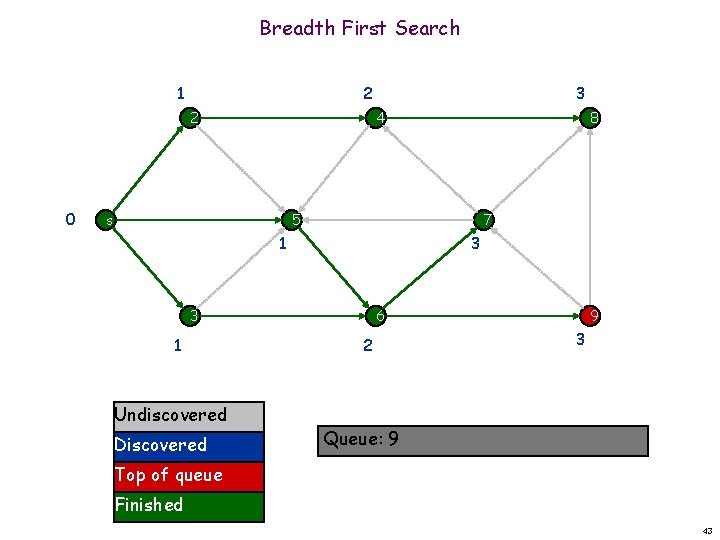
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 7 9 Top of queue Finished 40

Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 9 Top of queue Finished 41

Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 9 Top of queue Finished 42

Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 9 Top of queue Finished 43

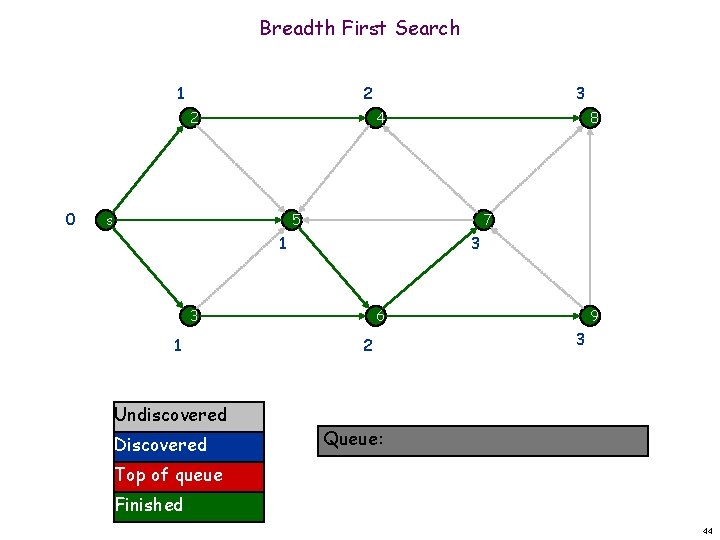
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: Top of queue Finished 44

Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 9 3 u Starting from s, we visited all (reachable) nodes u BFS forms a tree rooted at s (BFS Tree) u For each node x reachable from s we created a shortest path from s to x 45

Breadth First Search Example problems in which we use BFS u Find if node x is reachable from node y u Start from node y and do BFS u Find the shortest path from node x to node y u Start from node x and perform BFS u Search for a value v in the graph u Start from any node and perform BFS Always keep in mind whether we talk about undirected graph or directed graph 46

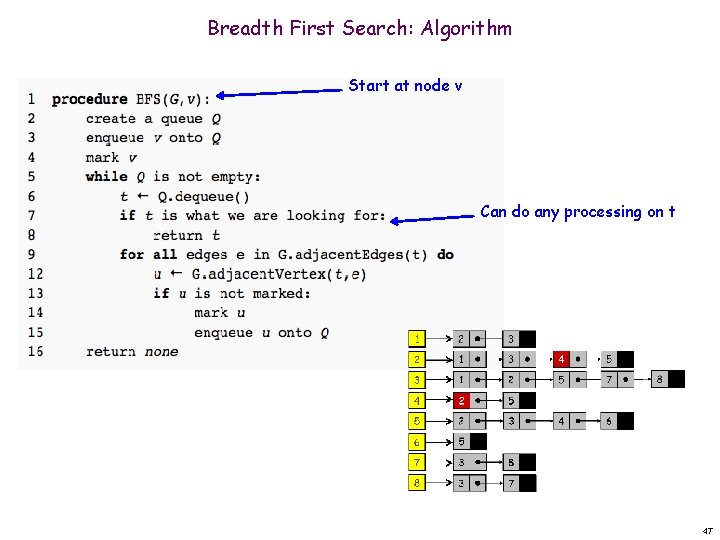
Breadth First Search: Algorithm Start at node v Can do any processing on t 47

Breadth First Search: Analysis Theorem. The above implementation of BFS runs in O(V + E) time if the graph is given by its adjacency list. Proof Each node will be queued only once O(V) For each node, we visit all its out edges O(E) – In fact each edge (u, v) is visited twice once from u’s side and once form v’s side n n n Total is O(V + E) 48
 What is the overlap of data set 1 and data set 2?
What is the overlap of data set 1 and data set 2? Total set awareness set consideration set
Total set awareness set consideration set Training set validation set test set
Training set validation set test set Phân độ lown
Phân độ lown Block av độ 2
Block av độ 2 Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Chiến lược kinh doanh quốc tế của walmart
Chiến lược kinh doanh quốc tế của walmart Tìm độ lớn thật của tam giác abc
Tìm độ lớn thật của tam giác abc Con hãy đưa tay khi thấy người vấp ngã
Con hãy đưa tay khi thấy người vấp ngã Tôn thất thuyết là ai
Tôn thất thuyết là ai Gây tê cơ vuông thắt lưng
Gây tê cơ vuông thắt lưng Sau thất bại ở hồ điển triệt
Sau thất bại ở hồ điển triệt How are the whale flipper and the human arm different
How are the whale flipper and the human arm different Networks and graphs circuits paths and graph structures
Networks and graphs circuits paths and graph structures What is state graph in software testing
What is state graph in software testing Speed and velocity
Speed and velocity Graphs that enlighten and graphs that deceive
Graphs that enlighten and graphs that deceive End behaviour chart
End behaviour chart Bounded set vs centered set
Bounded set vs centered set Fucntions
Fucntions Crisp set vs fuzzy set
Crisp set vs fuzzy set Crisp set vs fuzzy set
Crisp set vs fuzzy set Correspondence function examples
Correspondence function examples Cross connect data center
Cross connect data center The data debate
The data debate Btech smart class.com
Btech smart class.com Types of data structures in r
Types of data structures in r Oblivious data structures
Oblivious data structures Linux kernel data structures
Linux kernel data structures Introduction to data structures
Introduction to data structures Introduction to data structures
Introduction to data structures Ajit diwan iit bombay
Ajit diwan iit bombay Esoteric data structures
Esoteric data structures Geometric data structures
Geometric data structures Kevin wayne princeton
Kevin wayne princeton Data structures and algorithms tutorial
Data structures and algorithms tutorial Hadoop i/o
Hadoop i/o Recursive macro expansion
Recursive macro expansion Advanced data structures in java
Advanced data structures in java Assembler data structures
Assembler data structures Classic data structures by debasis samanta ppt
Classic data structures by debasis samanta ppt Persistent vs ephemeral data structures
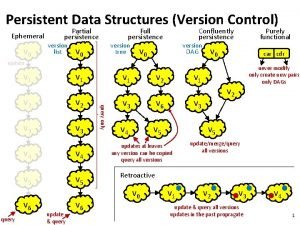
Persistent vs ephemeral data structures Php data structures
Php data structures Spatial data structures in gis
Spatial data structures in gis Information retrieval data structures and algorithms
Information retrieval data structures and algorithms Linked list java
Linked list java Recurrence data structures
Recurrence data structures Structures in c ppt
Structures in c ppt