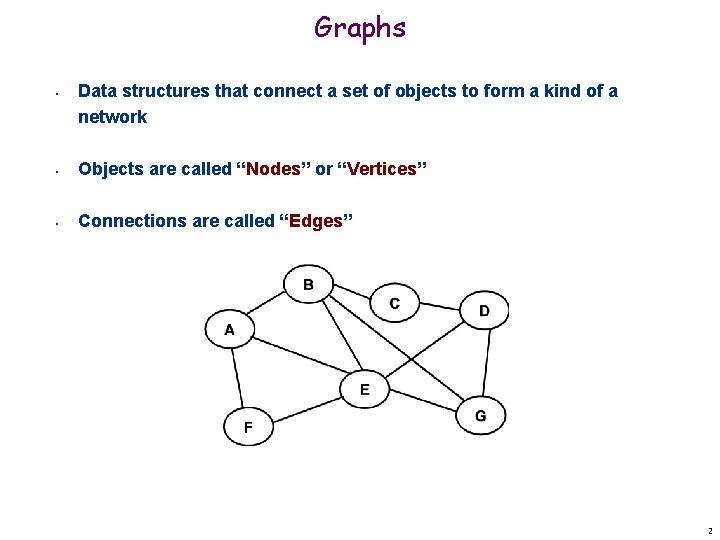
Graphs Graphs Data structures that connect a set
![Graph Representation: Adjacency Matrix Adjacency matrix. V-by-V matrix (A) n A[i, j] = 1](https://slidetodoc.com/presentation_image/008cc745c476e2ea27d5dcf2f99241ef/image-12.jpg "Graph Representation: Adjacency Matrix Adjacency matrix. V-by-V matrix (A) n A[i, j] = 1")
- Slides: 48
Graphs
Graphs • Data structures that connect a set of objects to form a kind of a network • Objects are called “Nodes” or “Vertices” • Connections are called “Edges” 2
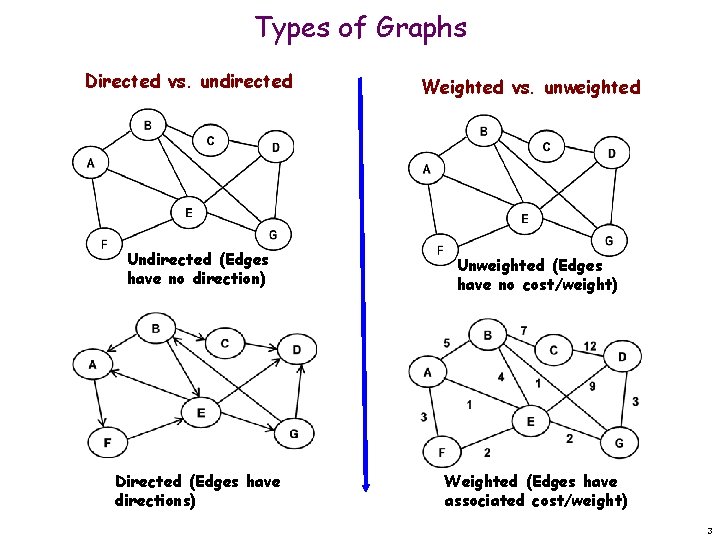
Types of Graphs Directed vs. undirected Weighted vs. unweighted Undirected (Edges have no direction) Unweighted (Edges have no cost/weight) Directed (Edges have directions) Weighted (Edges have associated cost/weight) 3
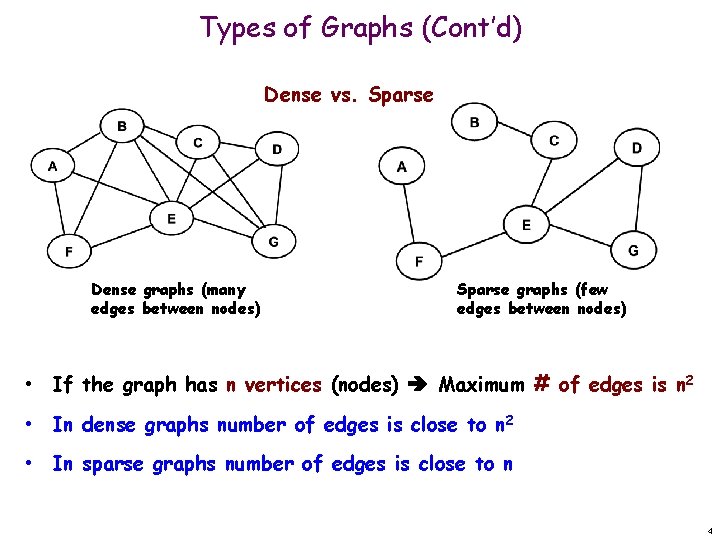
Types of Graphs (Cont’d) Dense vs. Sparse Dense graphs (many edges between nodes) Sparse graphs (few edges between nodes) • If the graph has n vertices (nodes) Maximum # of edges is n 2 • In dense graphs number of edges is close to n 2 • In sparse graphs number of edges is close to n 4
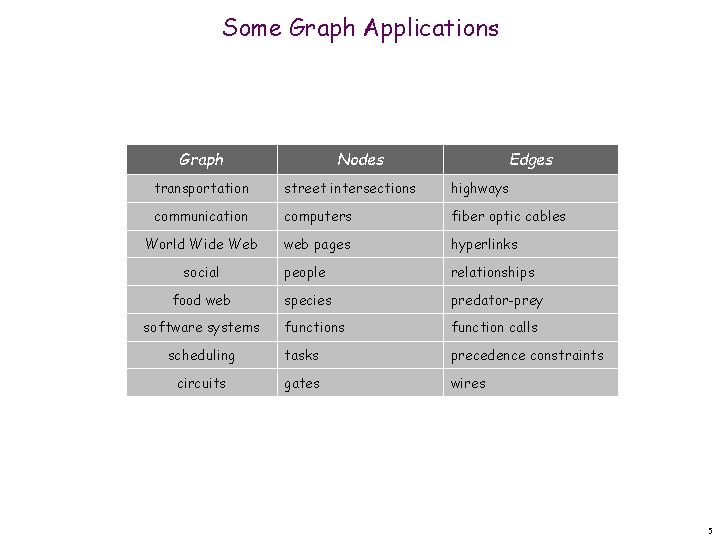
Some Graph Applications Graph Nodes Edges transportation street intersections highways communication computers fiber optic cables World Wide Web web pages hyperlinks social people relationships food web species predator-prey functions function calls scheduling tasks precedence constraints circuits gates wires software systems 5
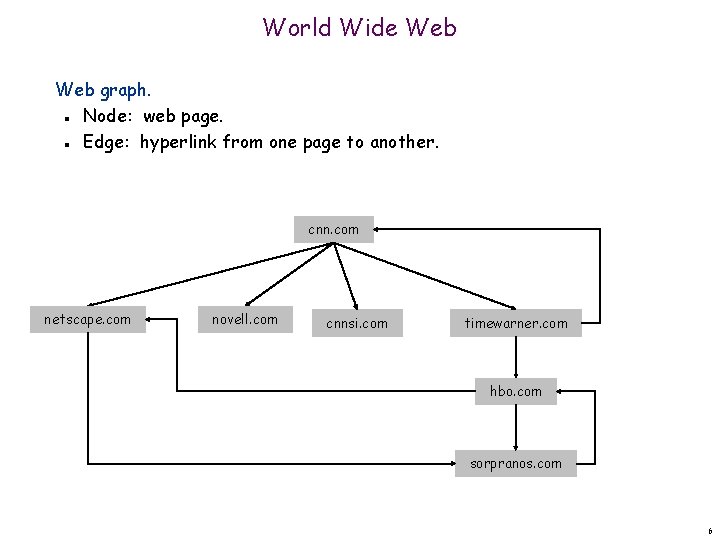
World Wide Web graph. Node: web page. Edge: hyperlink from one page to another. n n cnn. com netscape. com novell. com cnnsi. com timewarner. com hbo. com sorpranos. com 6
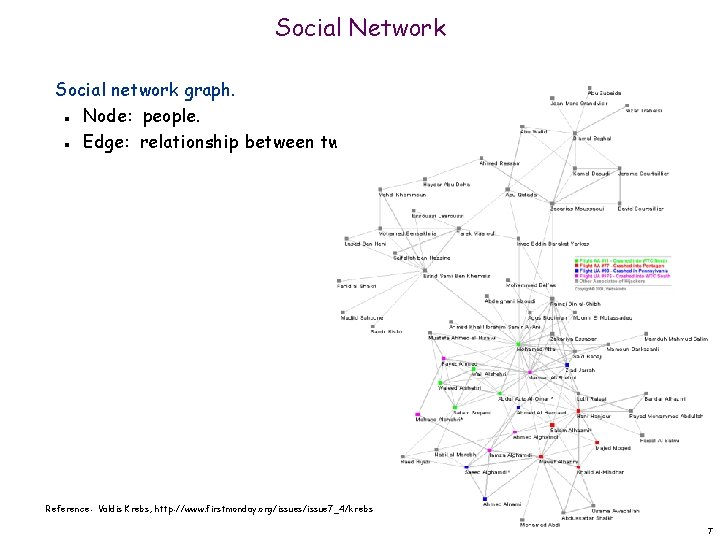
Social Network Social network graph. Node: people. Edge: relationship between two people. n n Reference: Valdis Krebs, http: //www. firstmonday. org/issues/issue 7_4/krebs 7
Protein Networks Nodes are proteins Edges are connections (interaction between proteins) 8
More Formalization 9
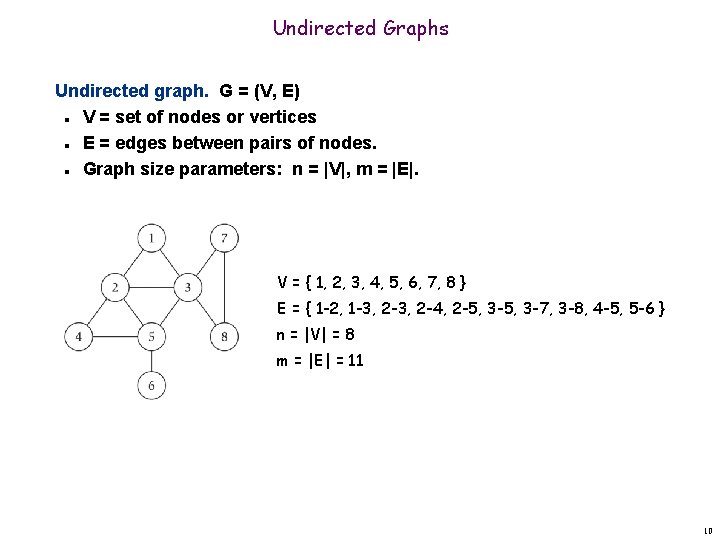
Undirected Graphs Undirected graph. G = (V, E) V = set of nodes or vertices E = edges between pairs of nodes. Graph size parameters: n = |V|, m = |E|. n n n V = { 1, 2, 3, 4, 5, 6, 7, 8 } E = { 1 -2, 1 -3, 2 -4, 2 -5, 3 -7, 3 -8, 4 -5, 5 -6 } n = |V| = 8 m = |E| = 11 10
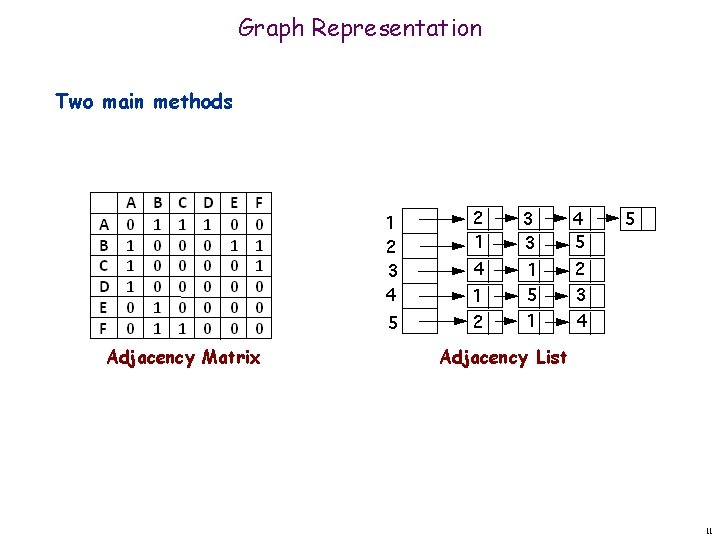
Graph Representation Two main methods Adjacency Matrix Adjacency List 11
Graph Representation: Adjacency Matrix Adjacency matrix. V-by-V matrix (A) n A[i, j] = 1 if exists edge between node i and node j n Space proportional to V 2 n Checking if (u, v) is an edge takes (1) time. n Identifying all edges takes (V 2) time. n For undirected graph matrix is symmetric across the diagonal Vertices 1 2 3 4 5 6 7 8 1 0 1 1 0 0 0 2 1 0 1 1 1 0 0 0 3 1 1 0 0 1 1 4 0 1 1 0 0 0 5 0 1 1 1 0 0 6 0 0 1 0 0 0 7 0 0 1 8 0 0 1 0 12
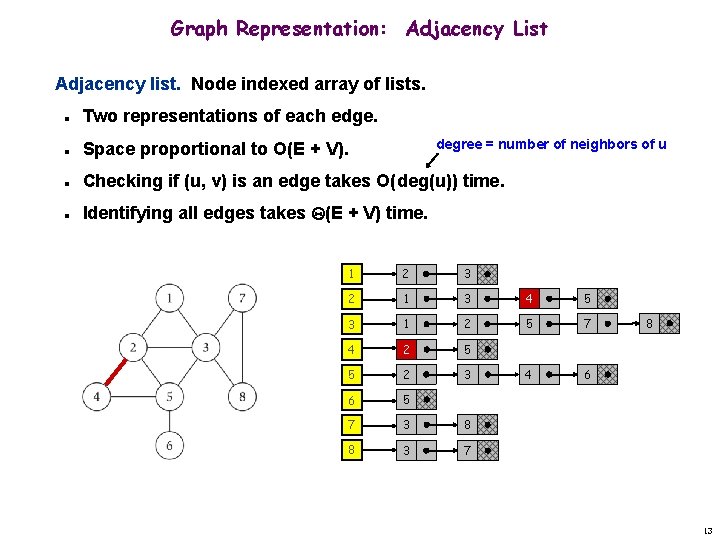
Graph Representation: Adjacency List Adjacency list. Node indexed array of lists. n Two representations of each edge. n Space proportional to O(E + V). n Checking if (u, v) is an edge takes O(deg(u)) time. n Identifying all edges takes (E + V) time. degree = number of neighbors of u 1 2 3 2 1 3 4 5 3 1 2 5 7 4 2 5 5 2 3 4 6 6 5 7 3 8 8 3 7 8 13
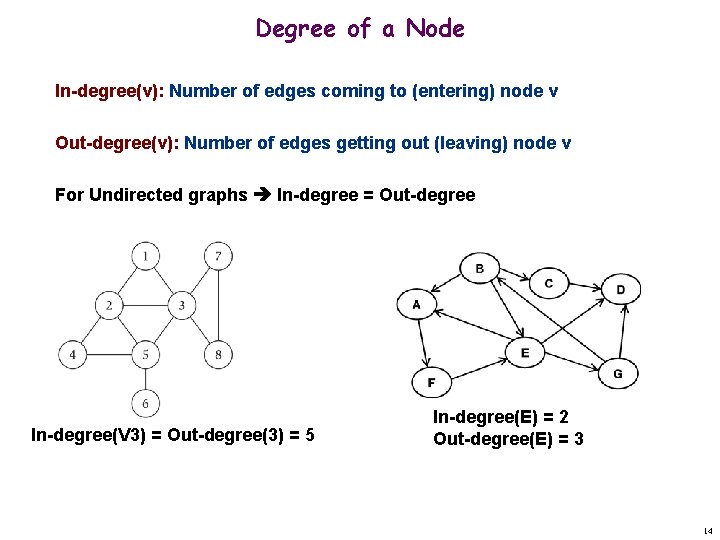
Degree of a Node In-degree(v): Number of edges coming to (entering) node v Out-degree(v): Number of edges getting out (leaving) node v For Undirected graphs In-degree = Out-degree In-degree(V 3) = Out-degree(3) = 5 In-degree(E) = 2 Out-degree(E) = 3 14
Graph Traversal 15
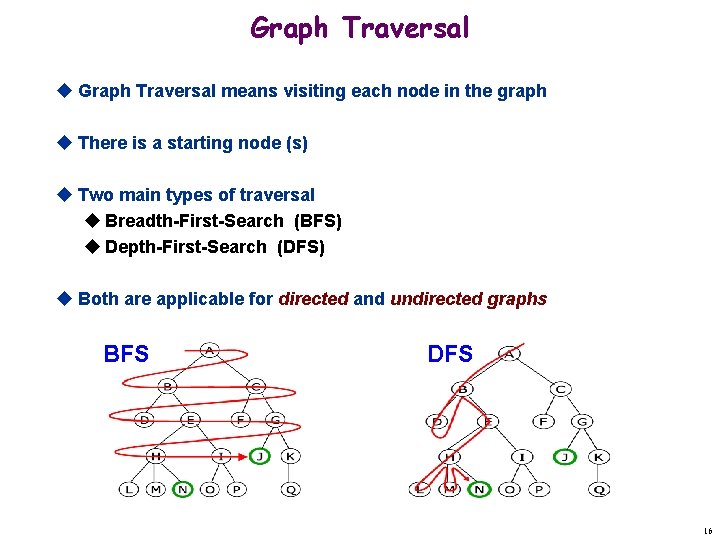
Graph Traversal u Graph Traversal means visiting each node in the graph u There is a starting node (s) u Two main types of traversal u Breadth-First-Search (BFS) u Depth-First-Search (DFS) u Both are applicable for directed and undirected graphs BFS DFS 16
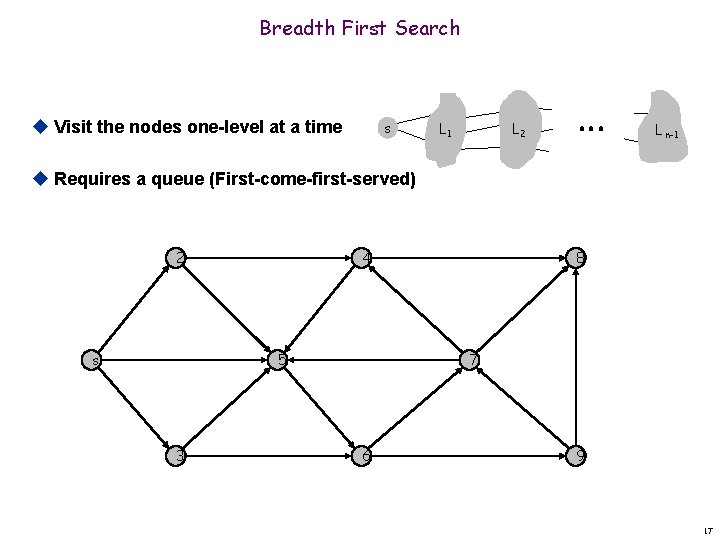
Breadth First Search u Visit the nodes one-level at a time s L 1 L 2 L n-1 u Requires a queue (First-come-first-served) 2 s 4 5 3 8 7 6 9 17
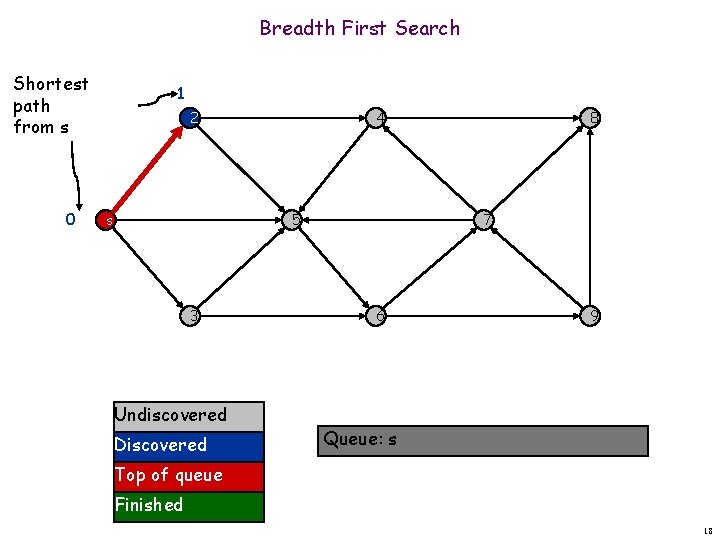
Breadth First Search Shortest path from s 0 1 2 s 4 5 3 Undiscovered Discovered 8 7 6 9 Queue: s Top of queue Finished 18
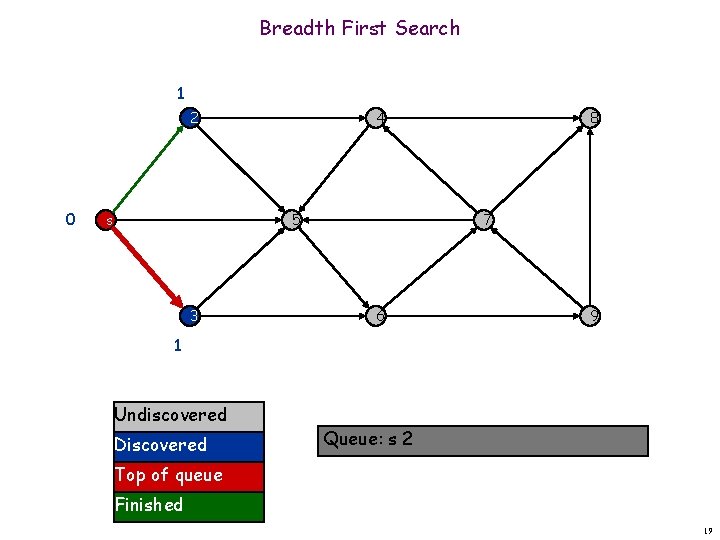
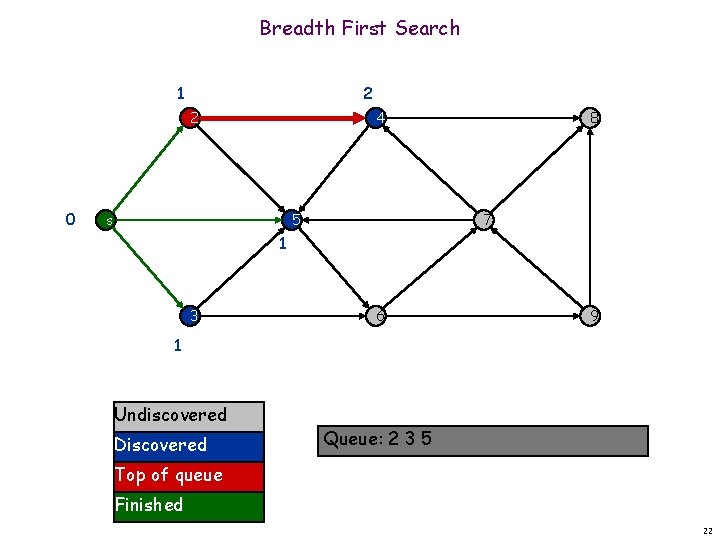
Breadth First Search 1 2 0 s 4 5 3 8 7 6 9 1 Undiscovered Discovered Queue: s 2 Top of queue Finished 19
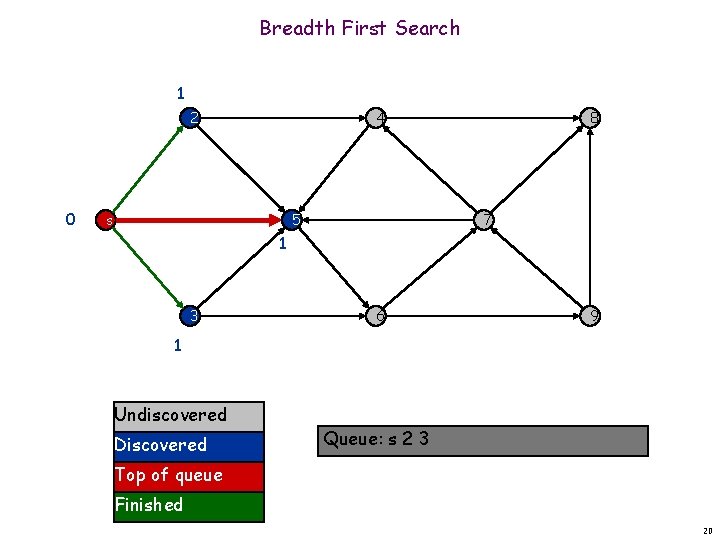
Breadth First Search 1 2 0 4 5 s 8 7 1 3 6 9 1 Undiscovered Discovered Queue: s 2 3 Top of queue Finished 20
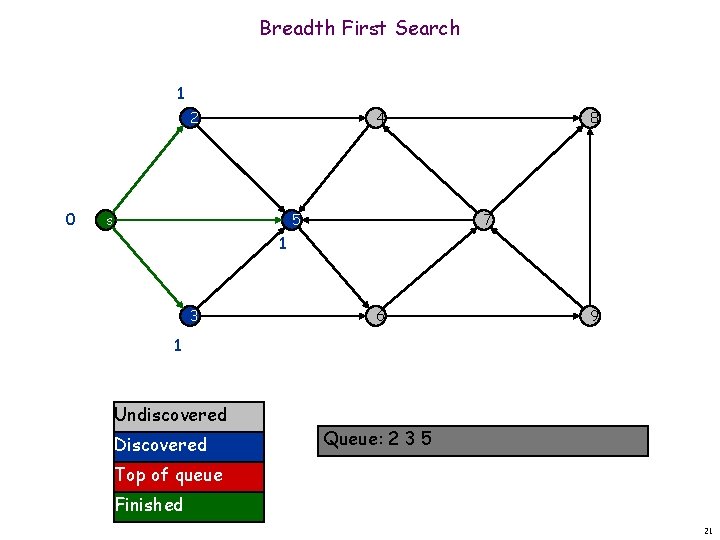
Breadth First Search 1 2 0 4 s 5 8 7 1 3 6 9 1 Undiscovered Discovered Queue: 2 3 5 Top of queue Finished 21
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 9 1 Undiscovered Discovered Queue: 2 3 5 Top of queue Finished 22
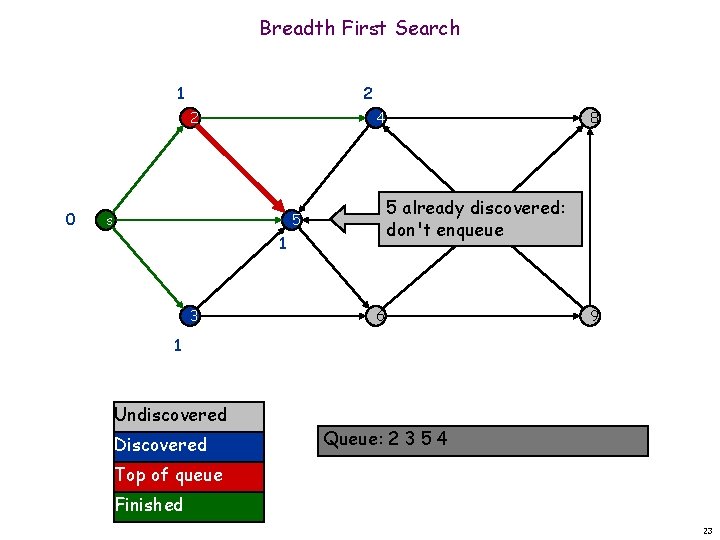
Breadth First Search 1 2 2 0 4 s 5 already discovered: 7 don't enqueue 5 1 3 8 6 9 1 Undiscovered Discovered Queue: 2 3 5 4 Top of queue Finished 23
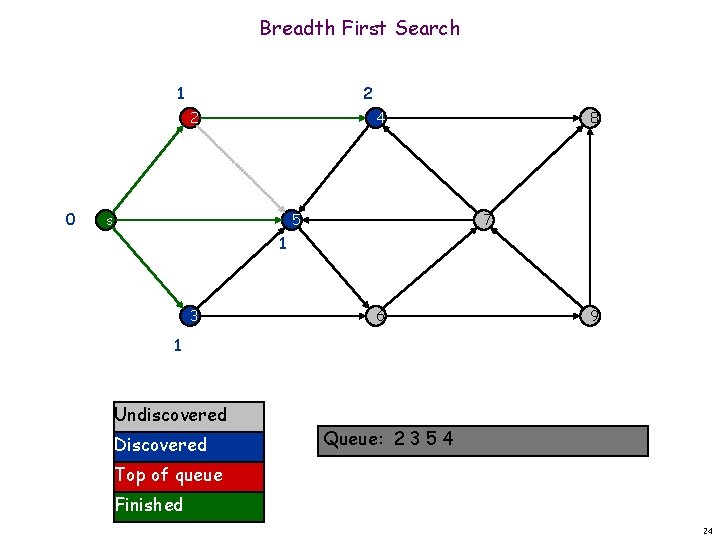
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 9 1 Undiscovered Discovered Queue: 2 3 5 4 Top of queue Finished 24
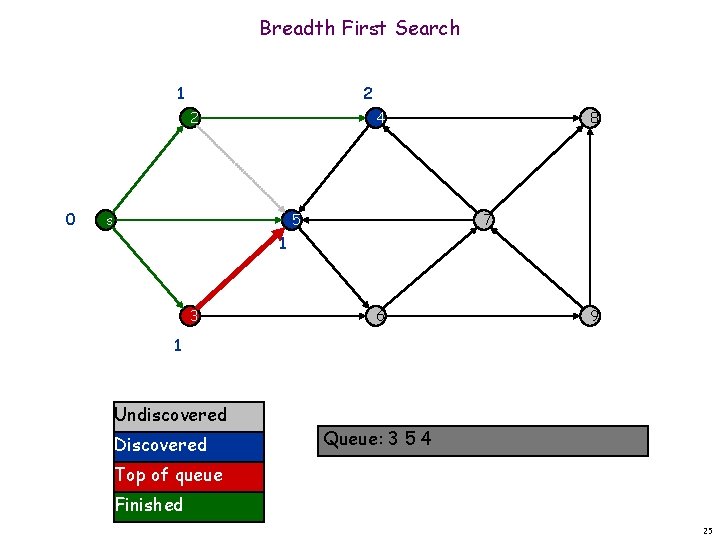
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 6 9 1 Undiscovered Discovered Queue: 3 5 4 Top of queue Finished 25
Breadth First Search 1 2 2 0 4 s 5 8 7 1 6 3 1 Undiscovered Discovered 9 2 Queue: 3 5 4 Top of queue Finished 26
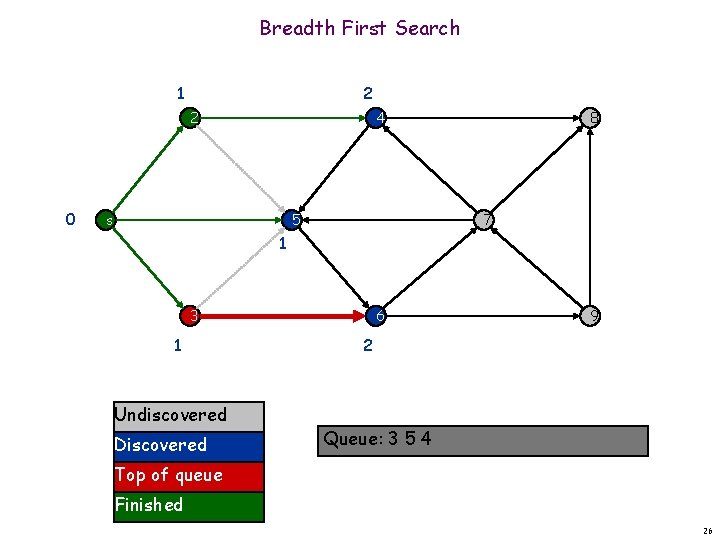
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 3 5 4 6 Top of queue Finished 27
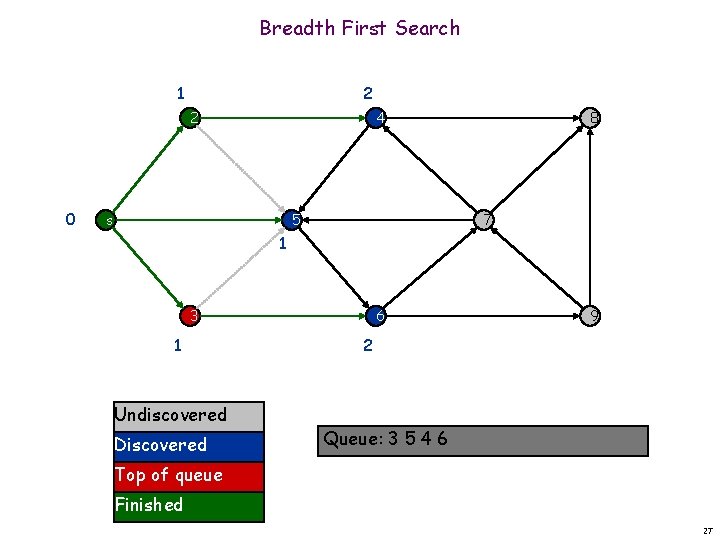
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 5 4 6 Top of queue Finished 28
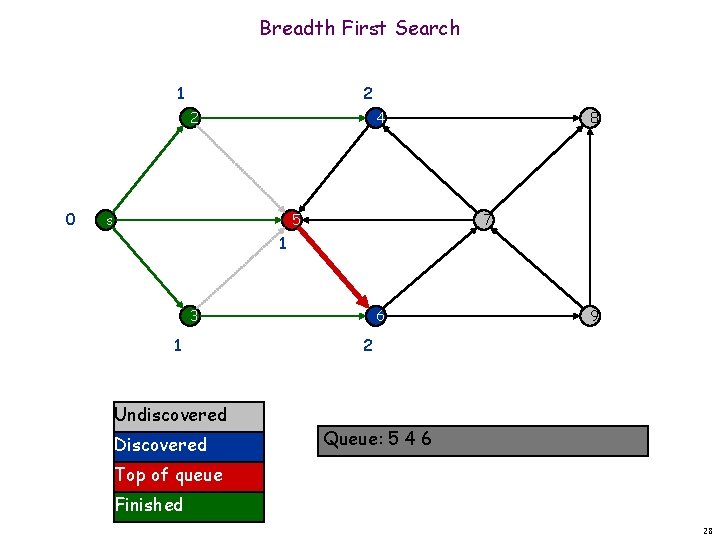
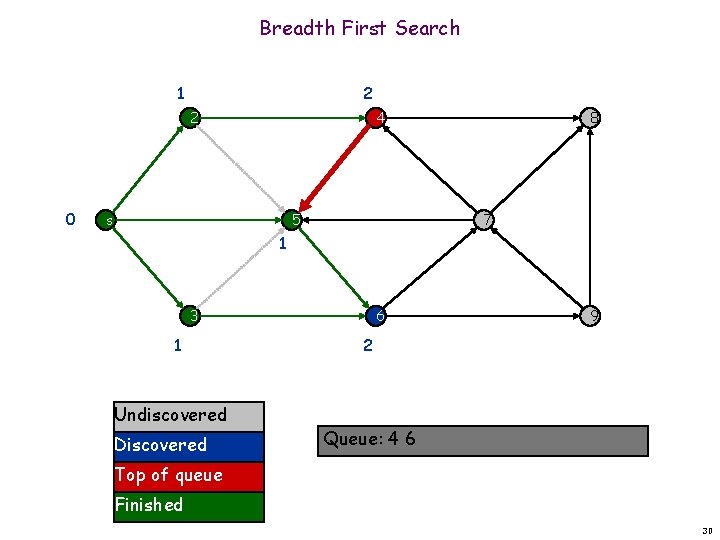
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 5 4 6 Top of queue Finished 29
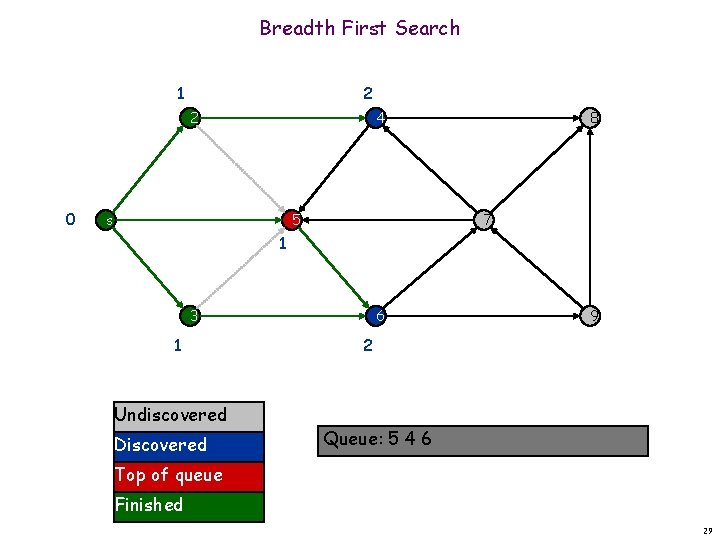
Breadth First Search 1 2 2 0 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 4 6 Top of queue Finished 30
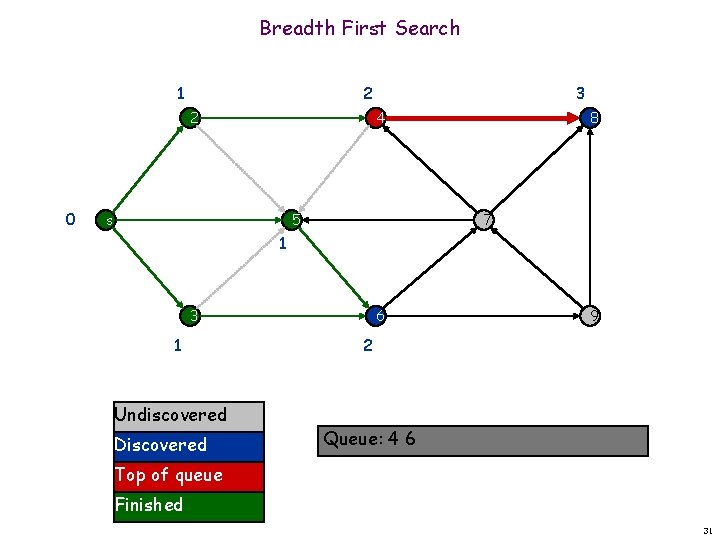
Breadth First Search 1 2 2 0 3 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 4 6 Top of queue Finished 31
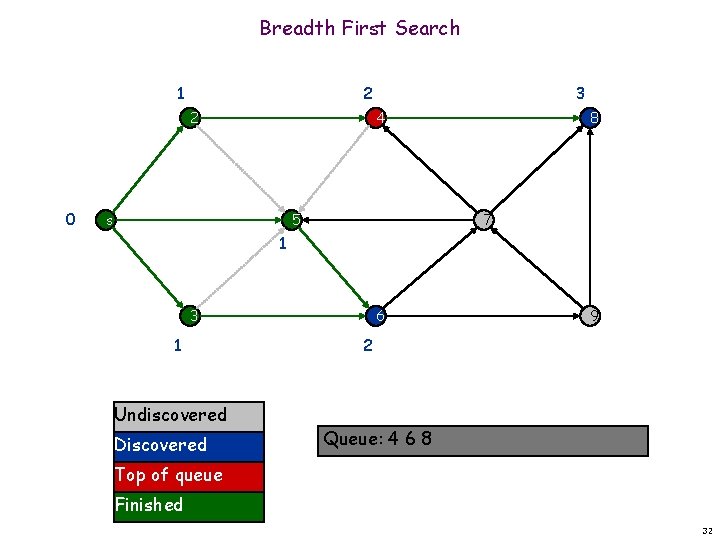
Breadth First Search 1 2 2 0 3 4 s 5 8 7 1 3 1 Undiscovered Discovered 6 9 2 Queue: 4 6 8 Top of queue Finished 32
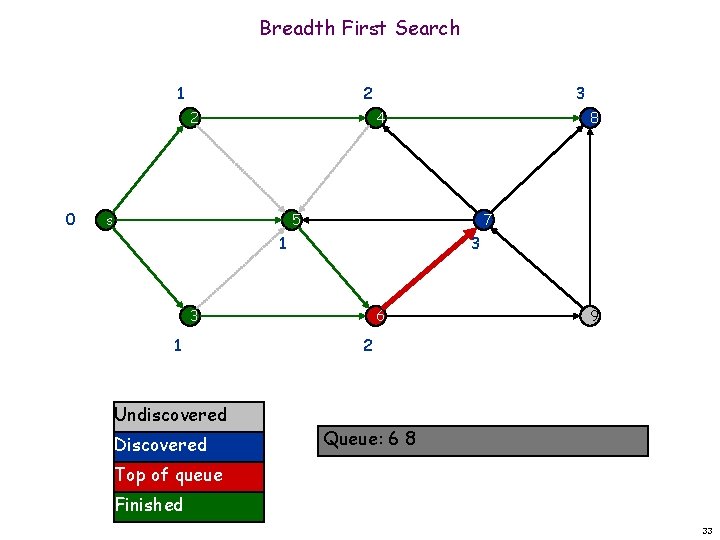
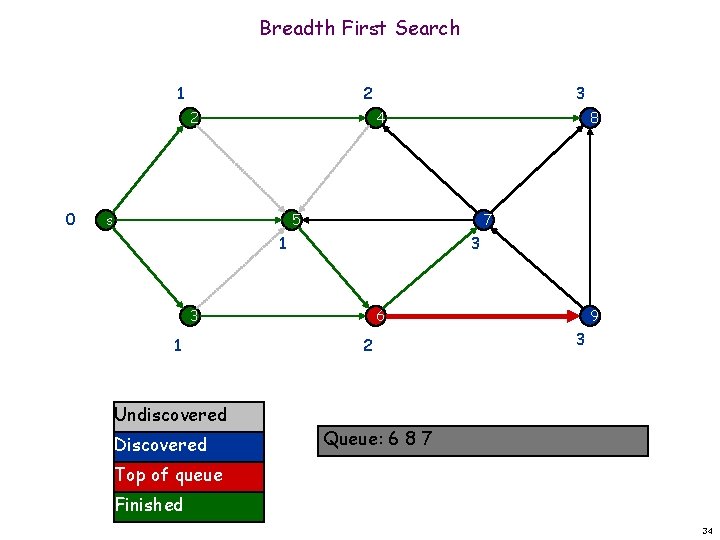
Breadth First Search 1 2 2 0 3 4 s 8 7 5 1 3 3 1 Undiscovered Discovered 6 9 2 Queue: 6 8 Top of queue Finished 33
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 6 8 7 Top of queue Finished 34
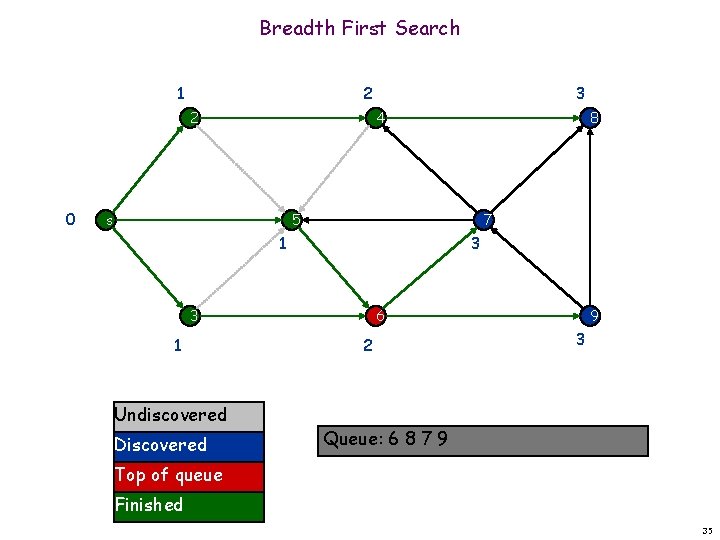
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 6 8 7 9 Top of queue Finished 35
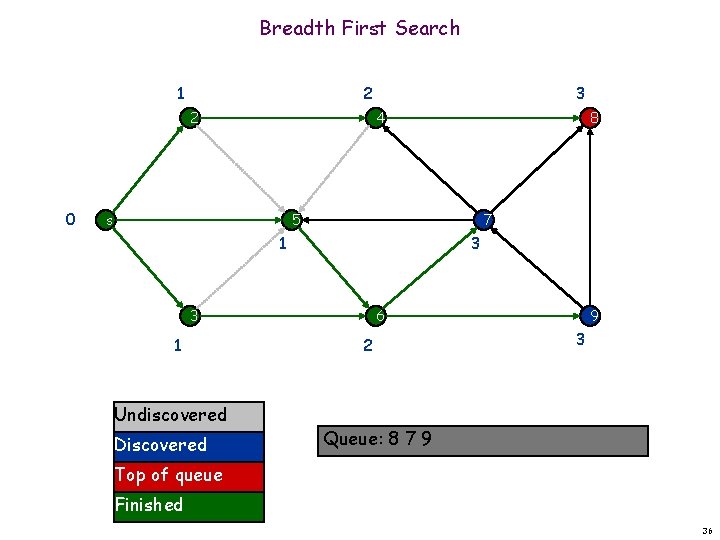
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 8 7 9 Top of queue Finished 36
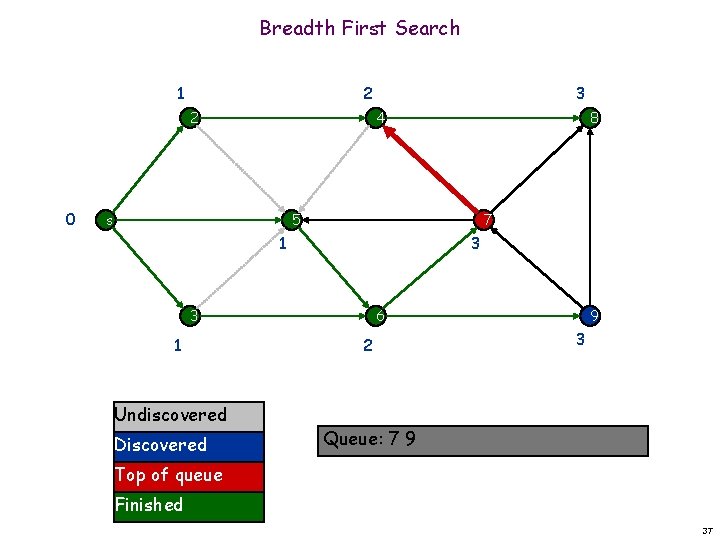
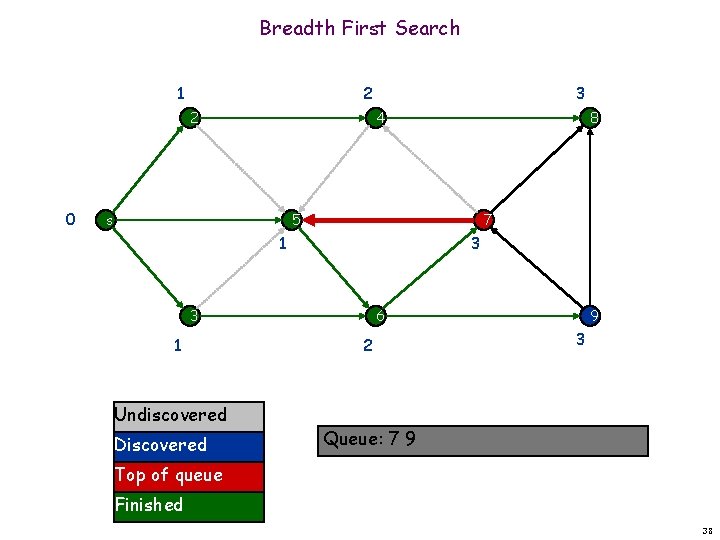
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 7 9 Top of queue Finished 37
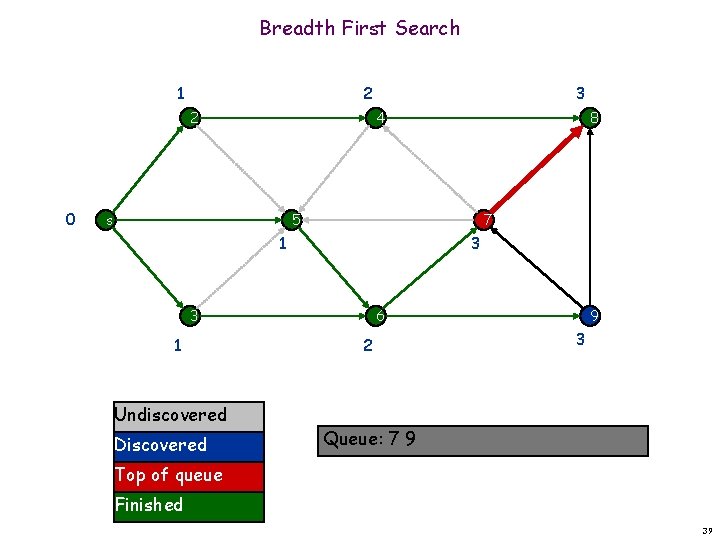
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 7 9 Top of queue Finished 38
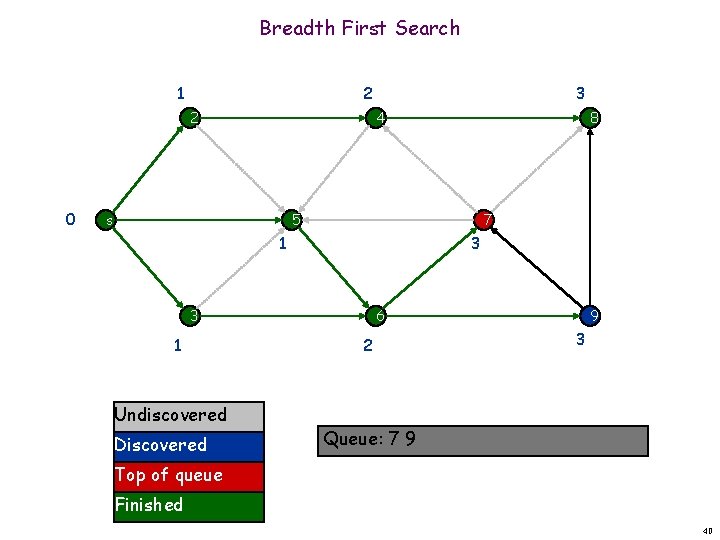
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 7 9 Top of queue Finished 39
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 7 9 Top of queue Finished 40
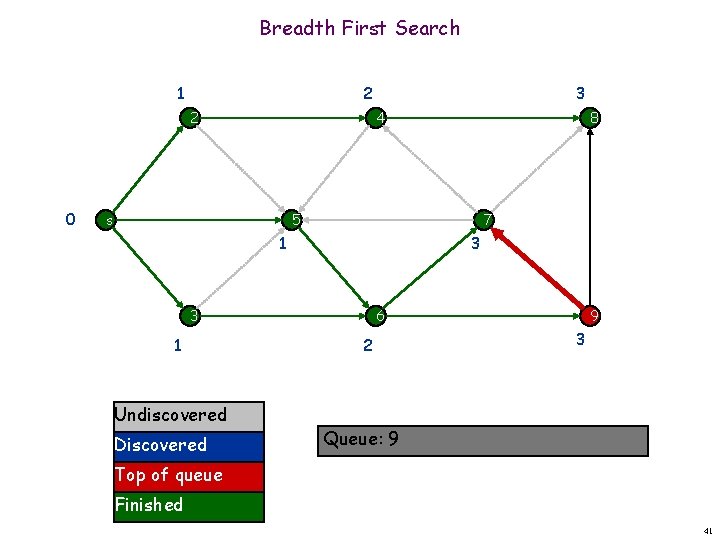
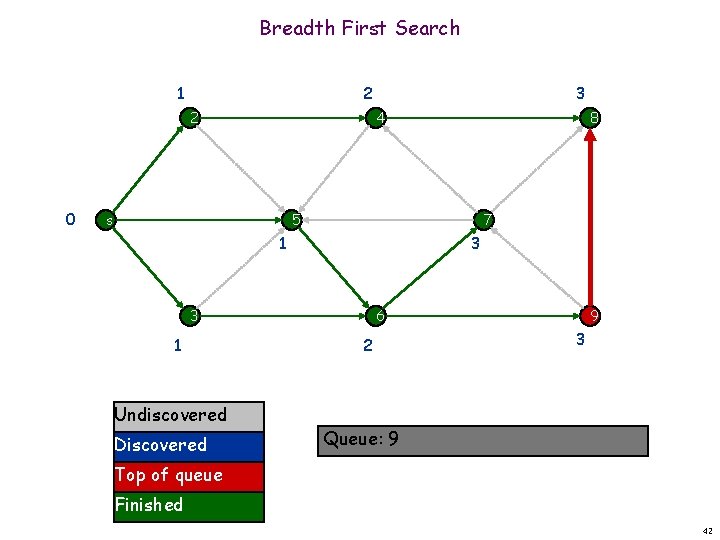
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 9 Top of queue Finished 41
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 9 Top of queue Finished 42
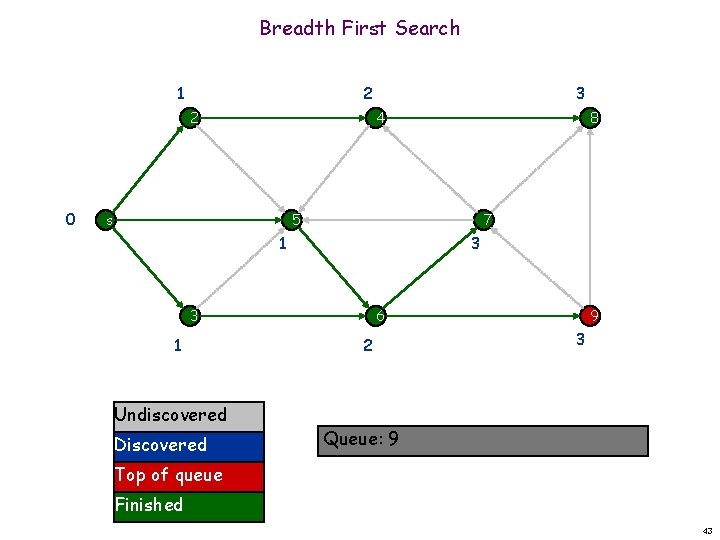
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: 9 Top of queue Finished 43
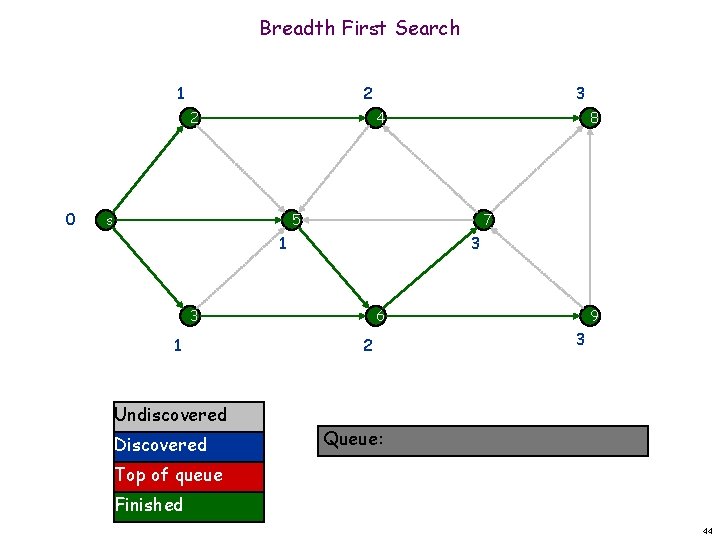
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 Undiscovered Discovered 6 2 9 3 Queue: Top of queue Finished 44
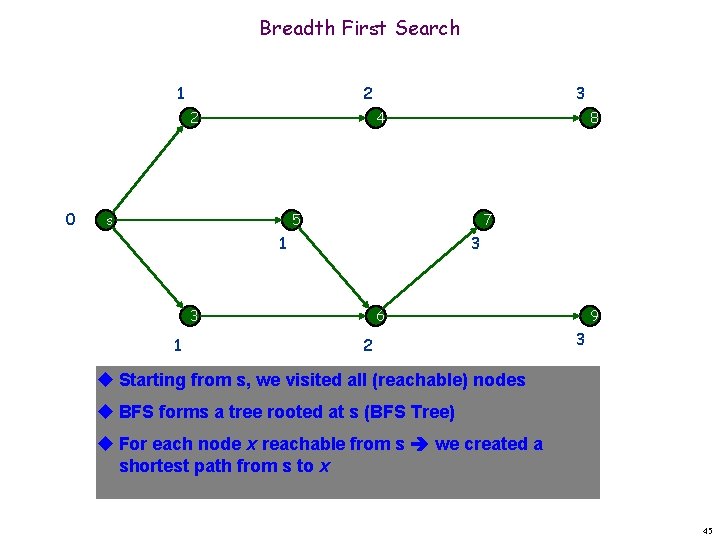
Breadth First Search 1 2 2 0 3 4 s 8 5 7 1 3 3 1 6 2 9 3 u Starting from s, we visited all (reachable) nodes u BFS forms a tree rooted at s (BFS Tree) u For each node x reachable from s we created a shortest path from s to x 45
Breadth First Search Example problems in which we use BFS u Find if node x is reachable from node y u Start from node y and do BFS u Find the shortest path from node x to node y u Start from node x and perform BFS u Search for a value v in the graph u Start from any node and perform BFS Always keep in mind whether we talk about undirected graph or directed graph 46
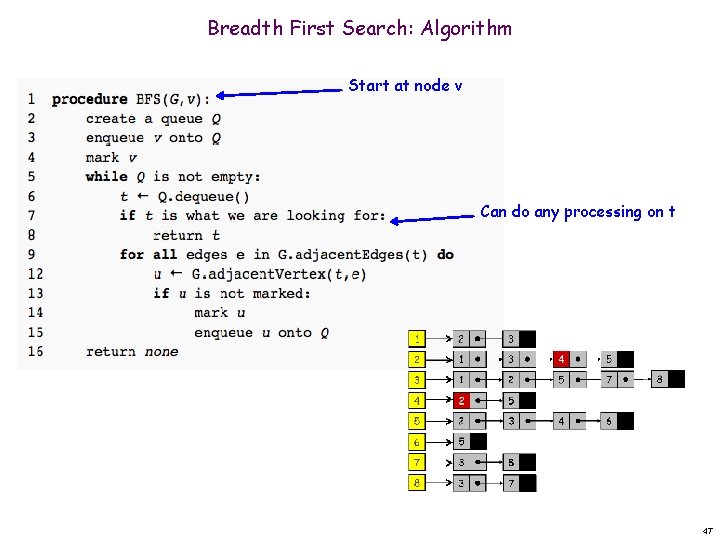
Breadth First Search: Algorithm Start at node v Can do any processing on t 47
Breadth First Search: Analysis Theorem. The above implementation of BFS runs in O(V + E) time if the graph is given by its adjacency list. Proof Each node will be queued only once O(V) For each node, we visit all its out edges O(E) – In fact each edge (u, v) is visited twice once from u’s side and once form v’s side n n n Total is O(V + E) 48