GRAPHS Graphs Data sometimes contains relationship between pairs

GRAPHS

Graphs Data sometimes contains relationship between pairs of elements which is not necessarily hierarchical in nature. Such type of data can be well modeled with the help of graphs

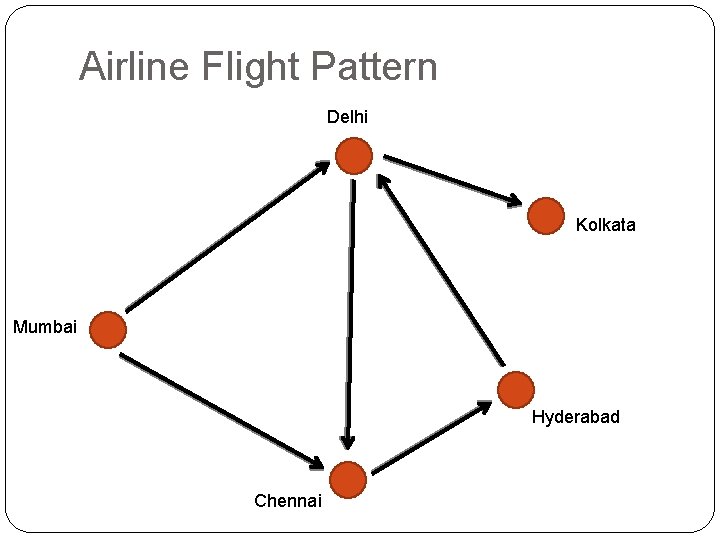
Airline Flight Pattern Delhi Kolkata Mumbai Hyderabad Chennai

Graphs A graph is a collection of nodes which are called ‘Vertices’ V, connected in pairs by line segments, called ‘Edges’ E. Types : 1. Undirected graph. 2. Directed graph.

Formal definition of graphs A graph G is defined as follows: G=(V, E) V(G): a finite, nonempty set of vertices E(G): a set of edges (pairs of vertices)

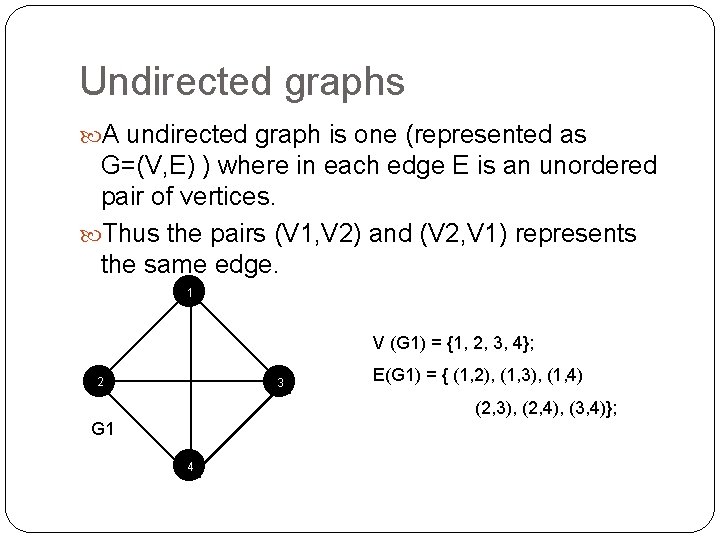
Undirected graphs A undirected graph is one (represented as G=(V, E) ) where in each edge E is an unordered pair of vertices. Thus the pairs (V 1, V 2) and (V 2, V 1) represents the same edge. 1 V (G 1) = {1, 2, 3, 4}; 2 3 E(G 1) = { (1, 2), (1, 3), (1, 4) (2, 3), (2, 4), (3, 4)}; G 1 4

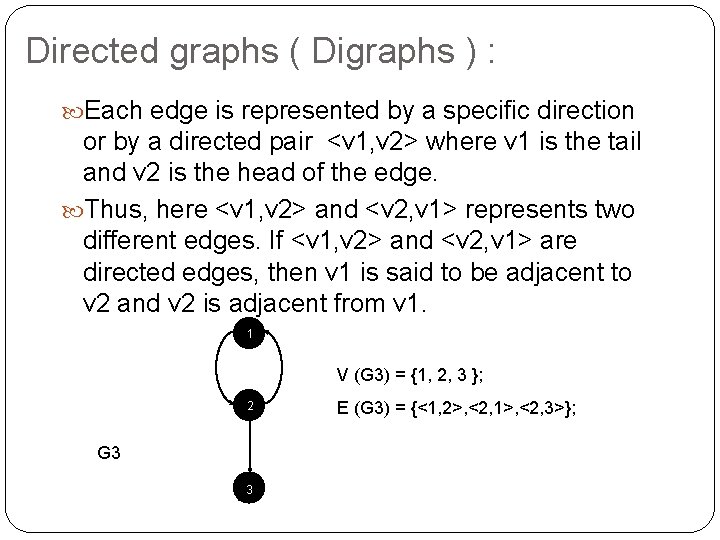
Directed graphs ( Digraphs ) : Each edge is represented by a specific direction or by a directed pair <v 1, v 2> where v 1 is the tail and v 2 is the head of the edge. Thus, here <v 1, v 2> and <v 2, v 1> represents two different edges. If <v 1, v 2> and <v 2, v 1> are directed edges, then v 1 is said to be adjacent to v 2 and v 2 is adjacent from v 1. 1 V (G 3) = {1, 2, 3 }; 2 G 3 3 E (G 3) = {<1, 2>, <2, 1>, <2, 3>};

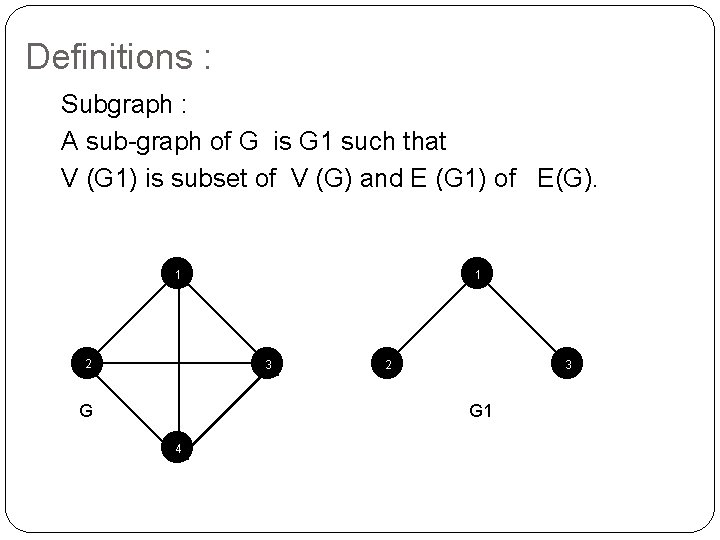
Definitions : Subgraph : A sub-graph of G is G 1 such that V (G 1) is subset of V (G) and E (G 1) of E(G). 1 2 1 3 G 2 3 G 1 4

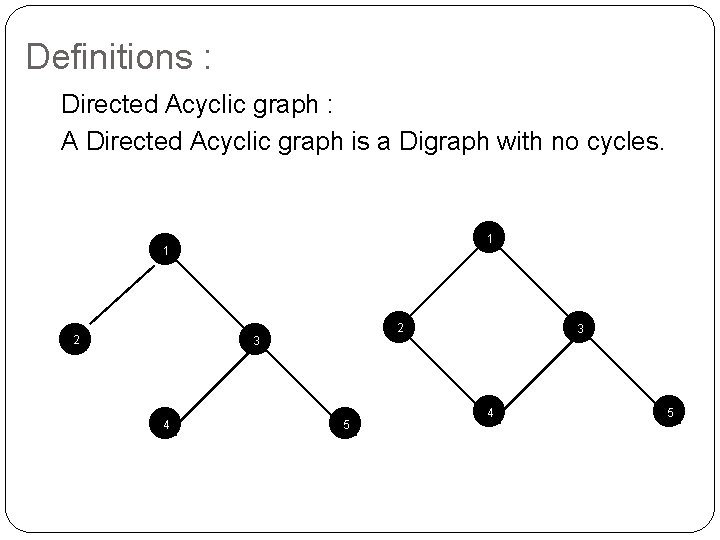
Definitions : Directed Acyclic graph : A Directed Acyclic graph is a Digraph with no cycles. 1 1 2 2 3 3 4 5

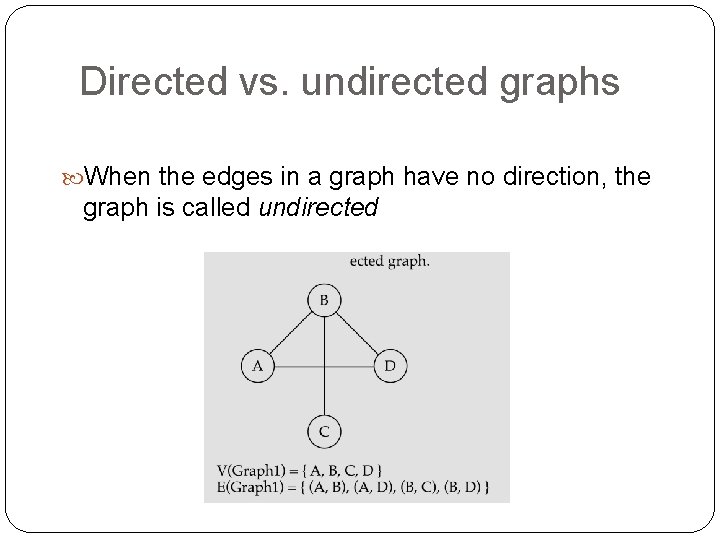
Directed vs. undirected graphs When the edges in a graph have no direction, the graph is called undirected

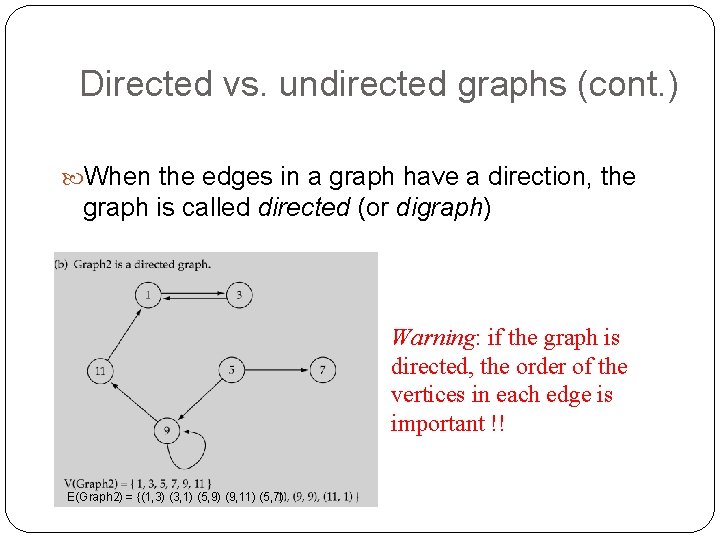
Directed vs. undirected graphs (cont. ) When the edges in a graph have a direction, the graph is called directed (or digraph) Warning: if the graph is directed, the order of the vertices in each edge is important !! E(Graph 2) = {(1, 3) (3, 1) (5, 9) (9, 11) (5, 7)

Graph terminology Adjacent nodes: two nodes are adjacent if they are connected by an edge 5 is adjacent to 7 7 is adjacent from 5 Complete graph: a graph in which every vertex is directly connected to every other vertex

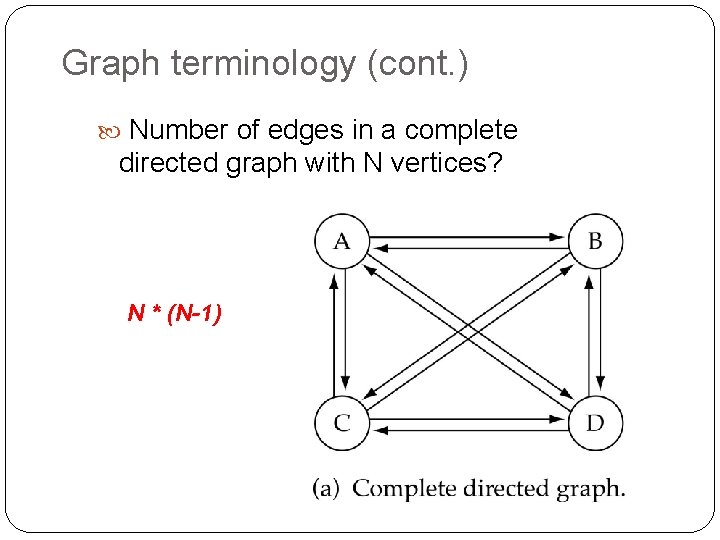
Graph terminology (cont. ) Number of edges in a complete directed graph with N vertices? N * (N-1)

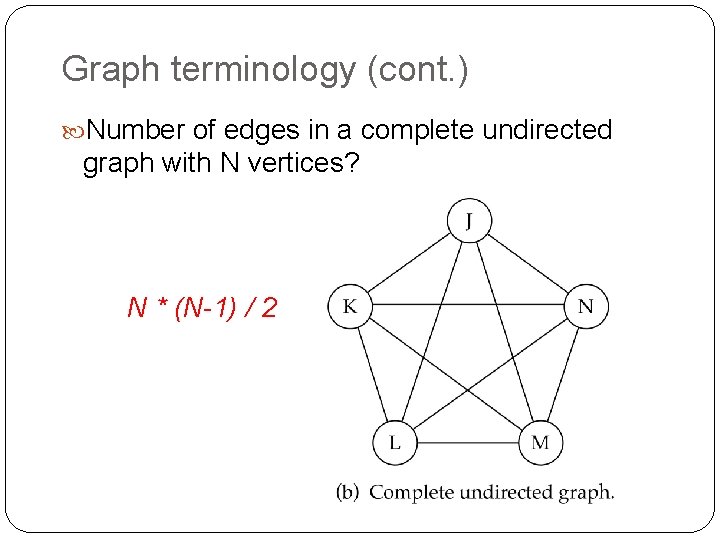
Graph terminology (cont. ) Number of edges in a complete undirected graph with N vertices? N * (N-1) / 2

Definitions : ADT Graph : Implementation of graphs : 1. Array method (Adjacency matrix) 2. Linked List (Adjacency lists)

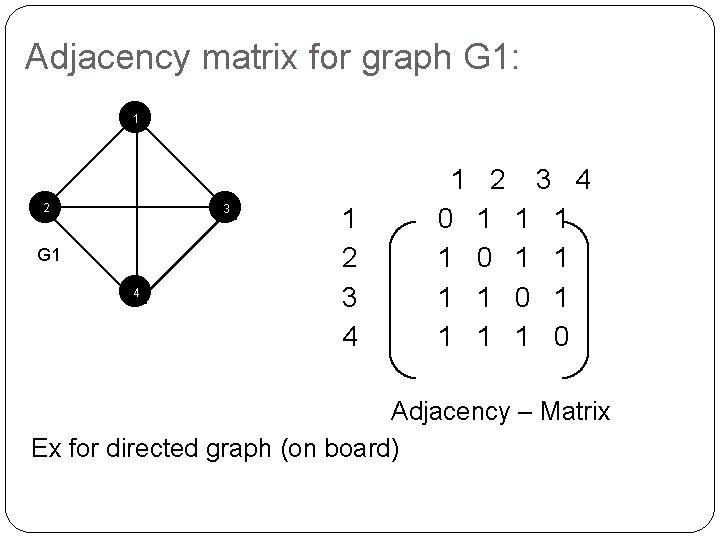
Adjacency matrix for graph G 1: 1 2 3 G 1 4 1 2 3 4 1 0 1 1 1 2 1 0 1 1 3 4 1 1 0 Adjacency – Matrix Ex for directed graph (on board)

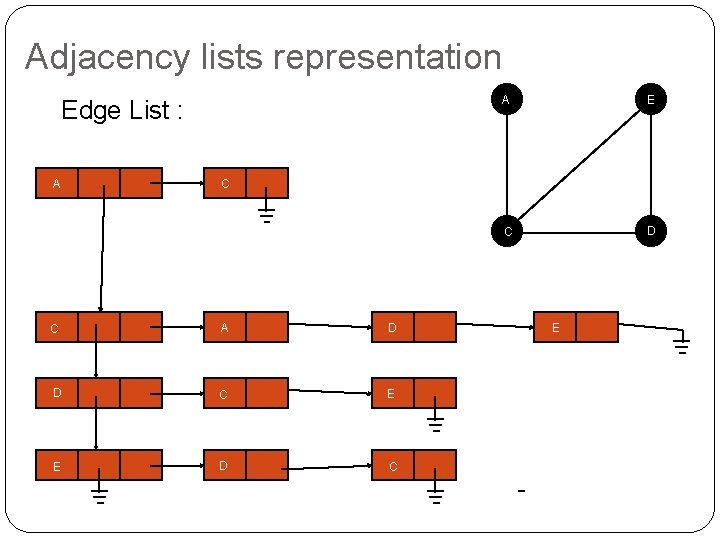
Adjacency lists representation Edge List : A A E C D C C A D D C E E D C E

Graph Traversal : Visiting all the nodes in a graph. Methods for traversal : 1. Depth - First - Search ( DFS ). 2. Breadth - First - Search ( BFS ).

Depth - First - Search ( DFS ) In this method a path is followed as deeply as possible. When there are no adjacent , nonvisited nodes , then we proceed backwards (backtrack) wherein we can repeat the process. A stack is maintained to keep track of the visited nodes. This helps backtracking.

Main steps of DFS : 1. Select any node in the graph. Mark this node as visited, push this node onto stack. 2. Find the adjacent node to the node on the top of stack, and which is not yet visited. Make this new node as visited and push onto stack. 3. Repeat step 2, until no new adjacent node to the top of the stack node can be found. When no new adjacent node can be found, pop the top of stack

Main steps of DFS (contd. . . ): 4. Repeat step 2 and 3 till stack becomes empty. 5. Repeat above steps, if there any more nodes which are still visited.

Breadth - First - Search (BFS): Nodes are examined across the breadth of the graph, before going to the next level. For BFS we use a queue. We pick a node to visit first and place its unprocessed adjacent nodes in queue. Repeatedly take a node from the front of the queue. If this node is unvisited, then we visit the node and then place all its neighbors in the queue.

Main steps of BFS : 1. Start with any node, mark it as visited. 2. Find the adjacent nodes, to the node marked in step 1. 3. Visit the node, which is at the front of queue. Delete it from queue and place its adjacent nodes in queue. 4. Repeat step 3, till the queue is not empty. 5. Stop.