Graphs Examples on some basic graph concepts and

Graphs Examples on some basic graph concepts and definitions All graphics are taken from the LEDA demos: basic_graph_algorithms, gw_shortest_paths, graphwin Geetika Tewari 252 a-al

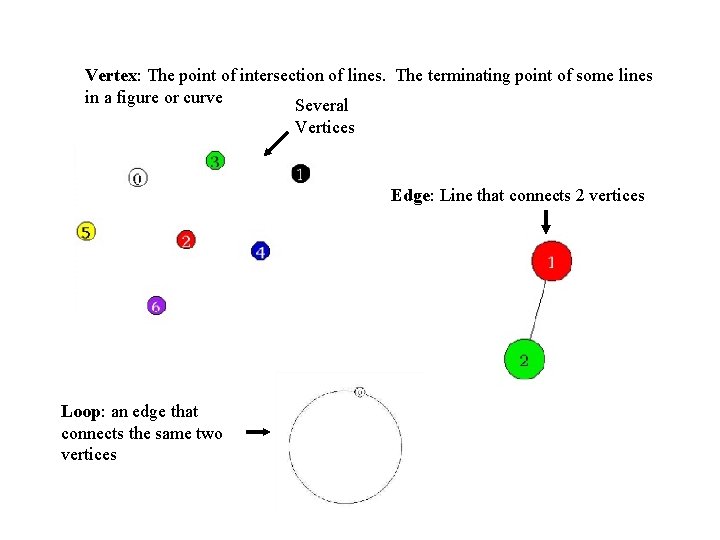
Vertex: The point of intersection of lines. The terminating point of some lines in a figure or curve Several Vertices Edge: Line that connects 2 vertices Loop: an edge that connects the same two vertices

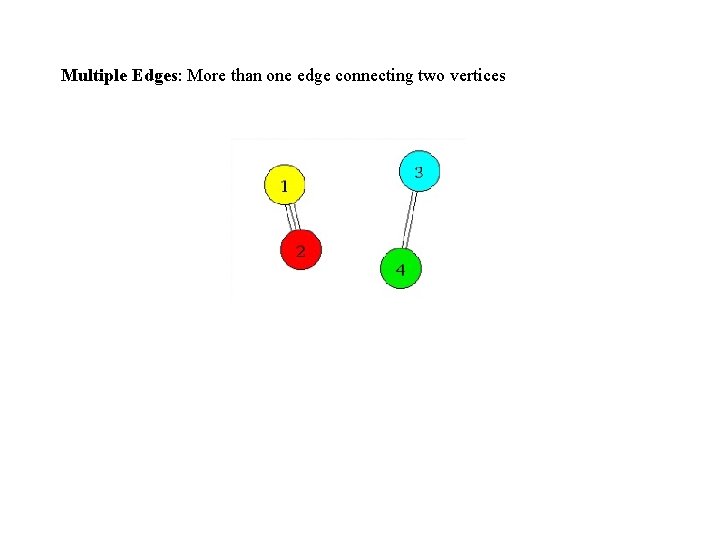
Multiple Edges: More than one edge connecting two vertices

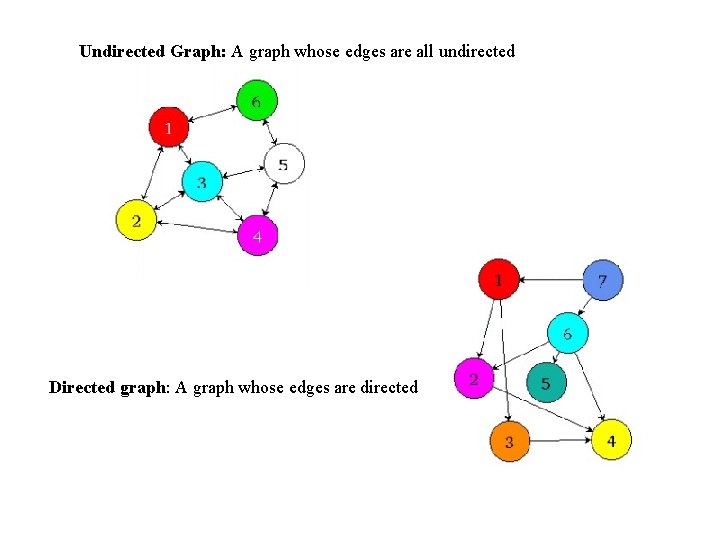
Undirected Graph: A graph whose edges are all undirected Directed graph: A graph whose edges are directed

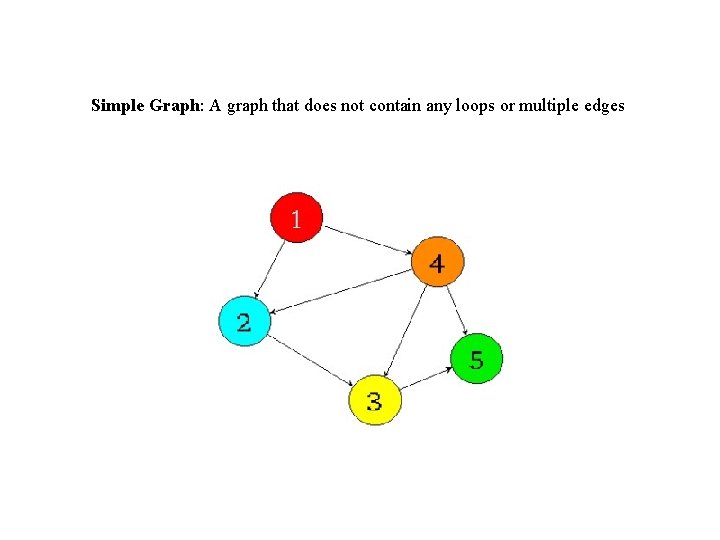
Simple Graph: A graph that does not contain any loops or multiple edges

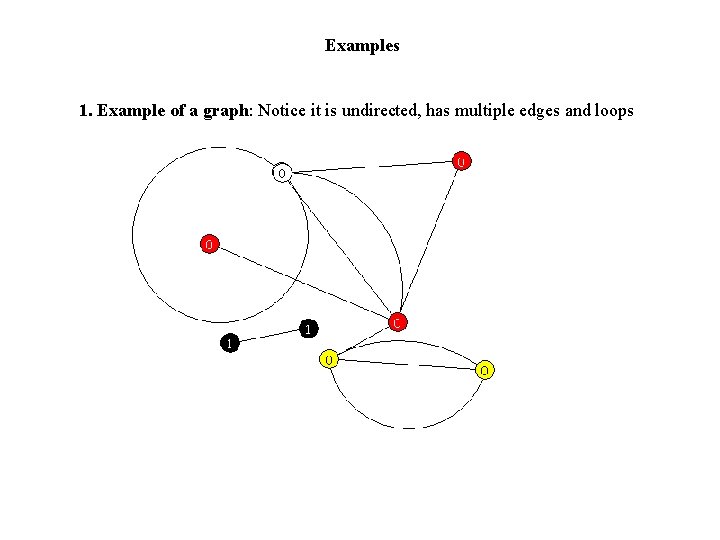
Examples 1. Example of a graph: Notice it is undirected, has multiple edges and loops

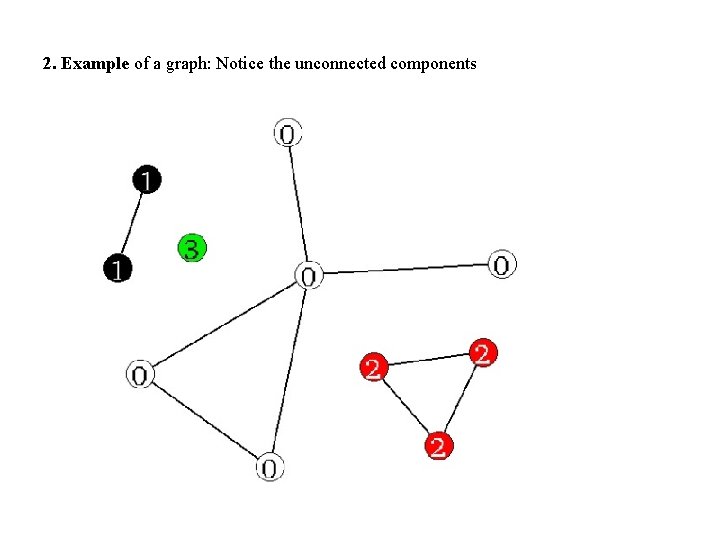
2. Example of a graph: Notice the unconnected components

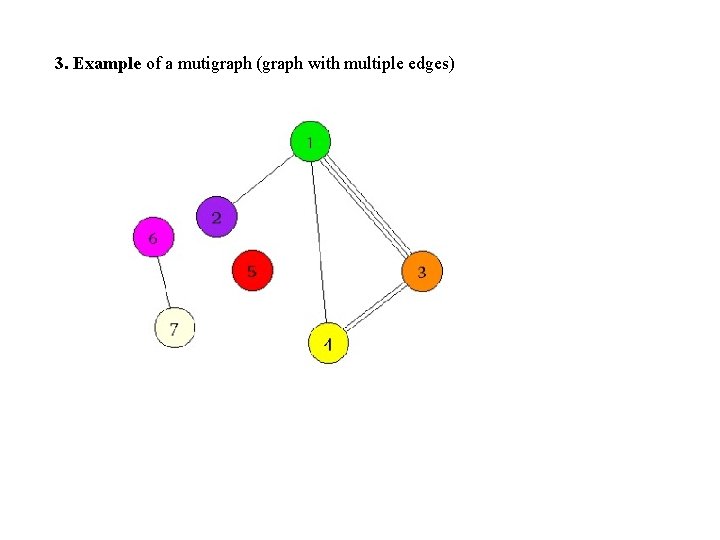
3. Example of a mutigraph (graph with multiple edges)

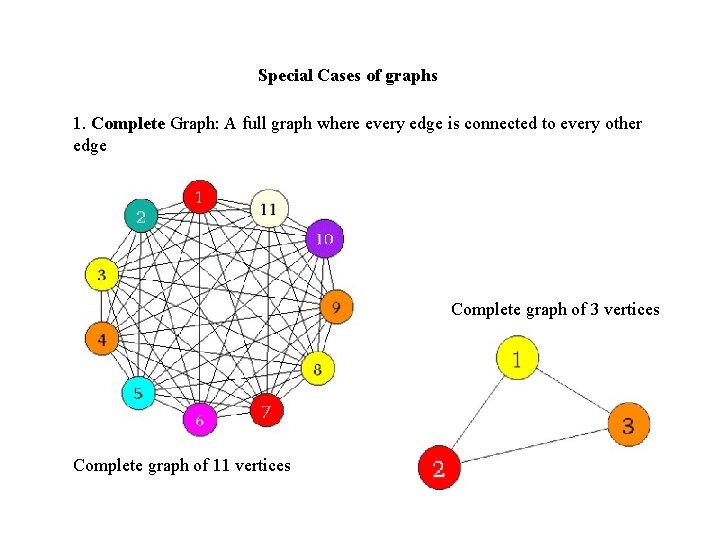
Special Cases of graphs 1. Complete Graph: A full graph where every edge is connected to every other edge Complete graph of 3 vertices Complete graph of 11 vertices

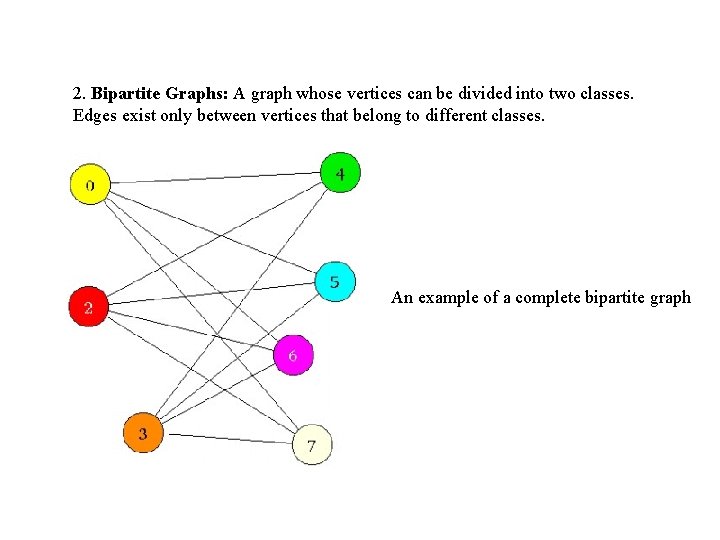
2. Bipartite Graphs: A graph whose vertices can be divided into two classes. Edges exist only between vertices that belong to different classes. An example of a complete bipartite graph

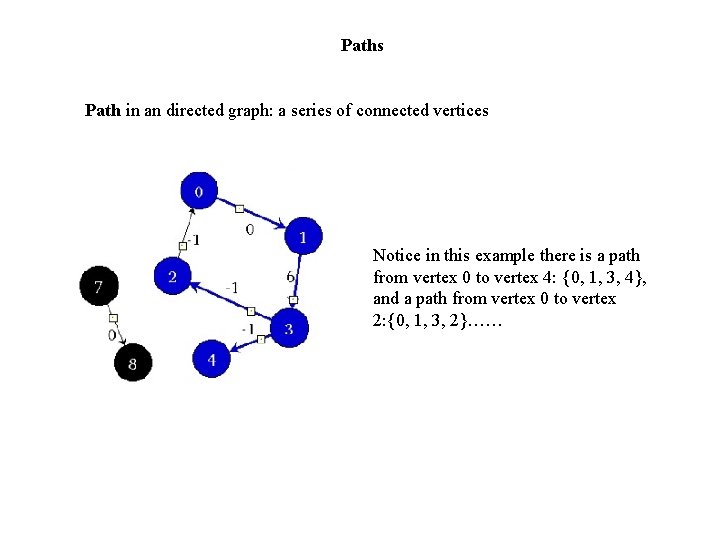
Paths Path in an directed graph: a series of connected vertices Notice in this example there is a path from vertex 0 to vertex 4: {0, 1, 3, 4}, and a path from vertex 0 to vertex 2: {0, 1, 3, 2}……

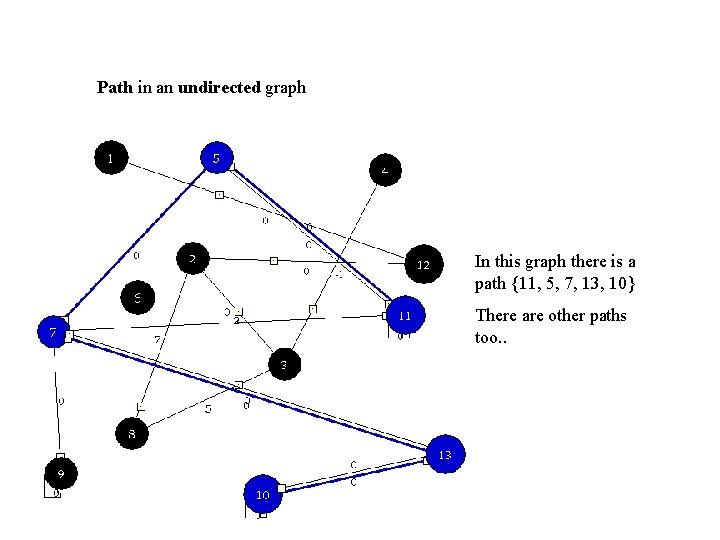
Path in an undirected graph In this graph there is a path {11, 5, 7, 13, 10} There are other paths too. .

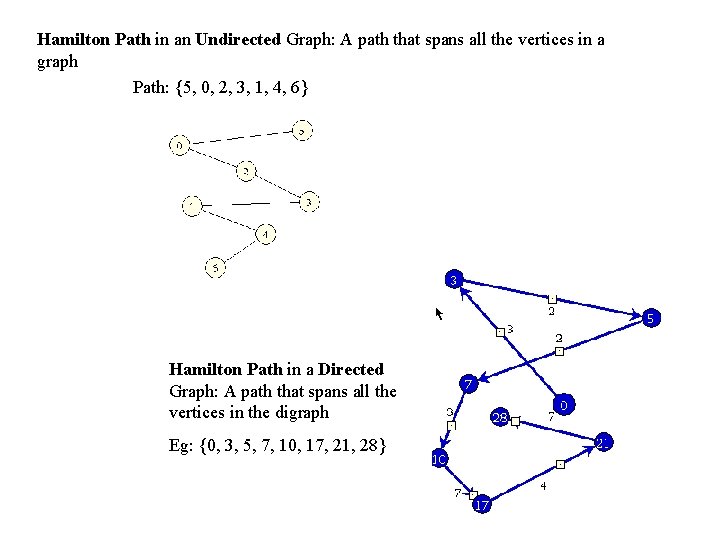
Hamilton Path in an Undirected Graph: A path that spans all the vertices in a graph Path: {5, 0, 2, 3, 1, 4, 6} Hamilton Path in a Directed Graph: A path that spans all the vertices in the digraph Eg: {0, 3, 5, 7, 10, 17, 21, 28}

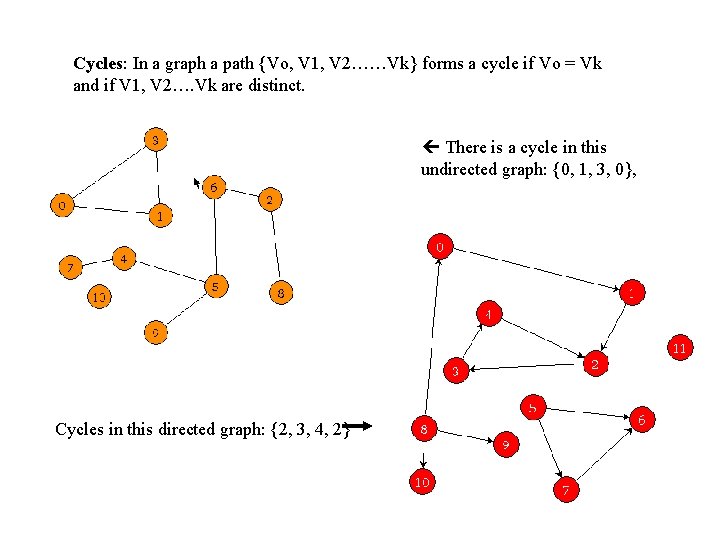
Cycles: In a graph a path {Vo, V 1, V 2……Vk} forms a cycle if Vo = Vk and if V 1, V 2…. Vk are distinct. There is a cycle in this undirected graph: {0, 1, 3, 0}, Cycles in this directed graph: {2, 3, 4, 2}

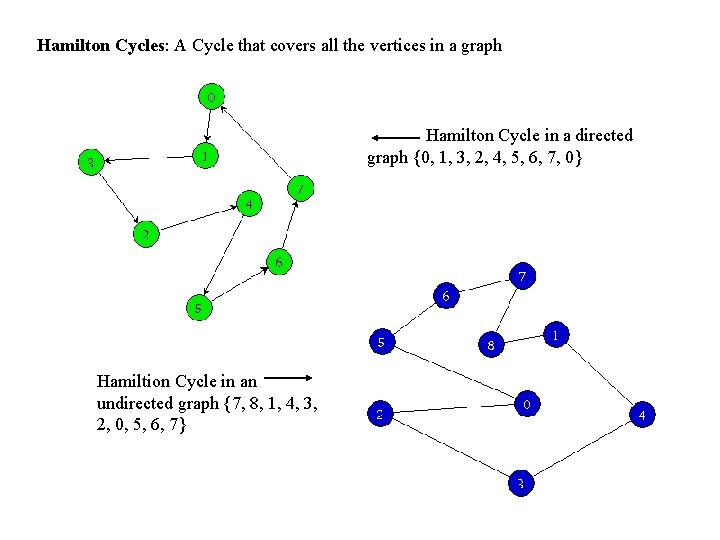
Hamilton Cycles: A Cycle that covers all the vertices in a graph Hamilton Cycle in a directed graph {0, 1, 3, 2, 4, 5, 6, 7, 0} Hamiltion Cycle in an undirected graph {7, 8, 1, 4, 3, 2, 0, 5, 6, 7}

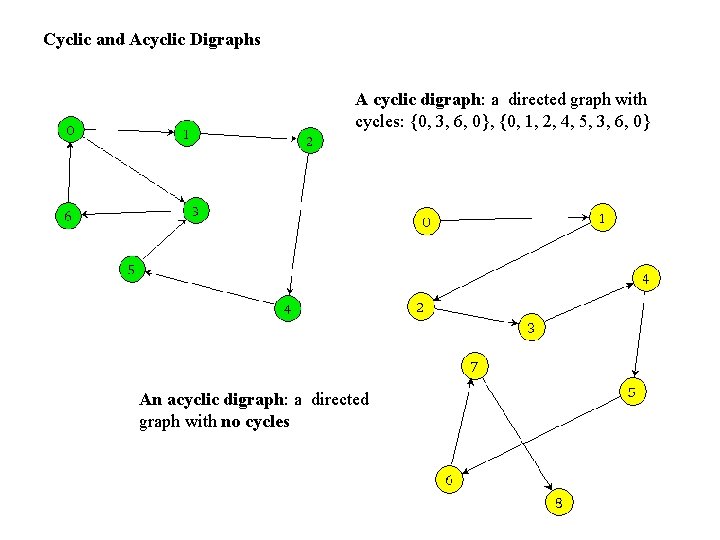
Cyclic and Acyclic Digraphs A cyclic digraph: a directed graph with cycles: {0, 3, 6, 0}, {0, 1, 2, 4, 5, 3, 6, 0} An acyclic digraph: a directed graph with no cycles

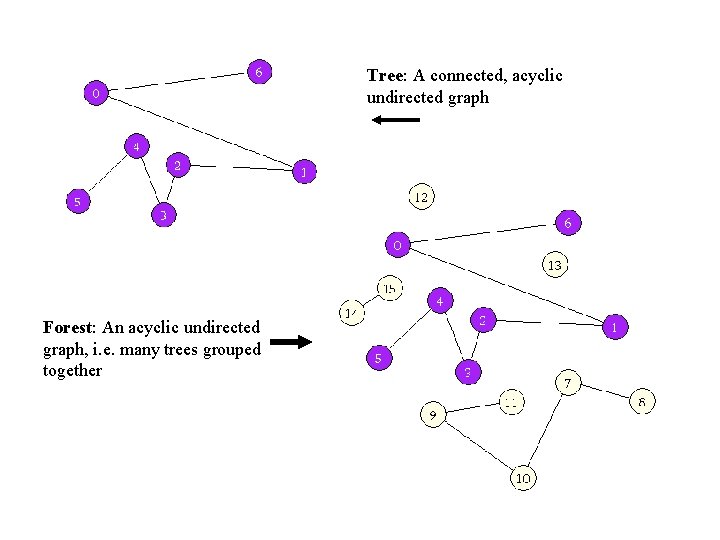
Tree: A connected, acyclic undirected graph Forest: An acyclic undirected graph, i. e. many trees grouped together

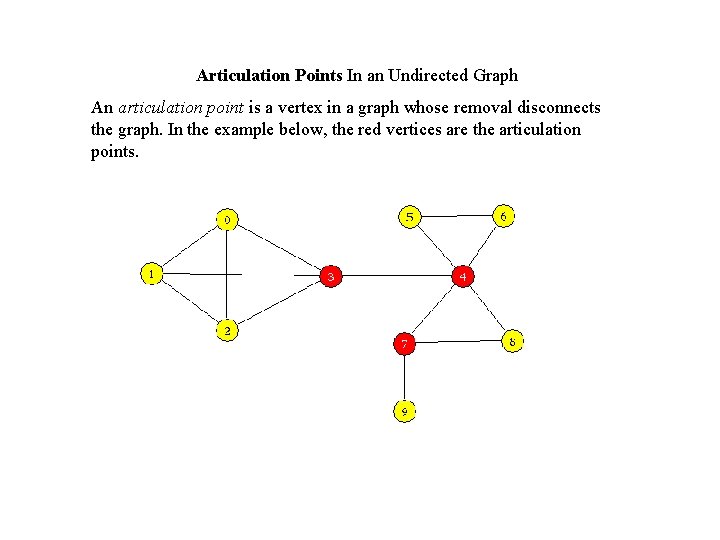
Articulation Points In an Undirected Graph An articulation point is a vertex in a graph whose removal disconnects the graph. In the example below, the red vertices are the articulation points.