GRAPHS Definition z The Graph Data Structure set

GRAPHS

Definition z. The Graph Data Structure Õset V of vertices Õcollection E of edges (pairs of vertices in V) z. Drawing of a Graph Õvertex <-> circle/oval Õedge <-> line connecting the vertex pair

Sample Uses z. Airports and flights z. Persons and acquaintance relationships z. Intersections and streets z. Computers and connections; the Internet

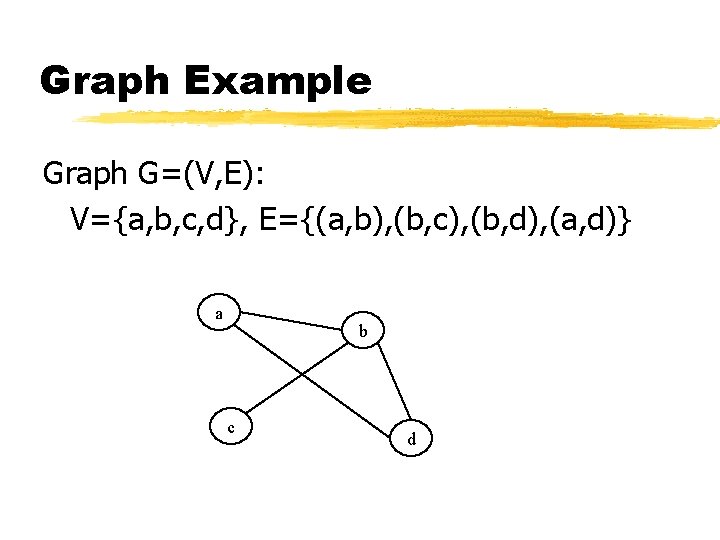
Graph Example Graph G=(V, E): V={a, b, c, d}, E={(a, b), (b, c), (b, d), (a, d)} a b c d

Adjacency z. Vertices connected by an edge are adjacent z. An edge e is incident on a vertex v (and vice-versa) if v is an endpoint of e z. Degree of a vertex v, deg(v) Õnumber of edges incident on v Õif directed graph, indeg(v) and outdeg(v)

Graph Properties Graph G with n vertices and m edges z v in G deg(v) = 2 m z v in G indeg(v) = v in G outdeg(v) = m zm is O(n 2) Õm <= n(n-1)/2 if G is undirected Õm <= n(n-1) if G is directed

Subgraphs z. Graph H a subgraph of graph G Õvertex set of H is a subset of vertex set of G Õedge set of H is a subset of edge set of G z. Spanning subgraph Õvertex set of H identical to vertex set of G

Paths and Cycles z(simple) Path Õsequence of distinct vertices such that consecutive vertices are connected through edges z(simple) Cycle Õsame as path except that first and last vertices are identical z. Directed paths and cycles Õedge directions matter

Connectivity z. Connected graph Õthere is a path between any two vertices

Graph Methods z. Container methods z. General or Global methods Õnum. Vertices(), num. Edges(), vertices(), edges() z. Directed Edge methods Õindegree(v), inadjacent. Vertices(v), inincident. Edges(v) z. Update methods Õadding/removing vertices or edges

General Methods z numvertices() -returns the number of vertices in G z numedges() - returns the number of edges in G z vertices() - return an enumeration of the vertex positions in G z edges() - returns an enumeration of the edge positions in G

General Methods z Degree (v) - returns the degree of v z adjacentvertices(v) - returns an enumeration of the vertices adjacent to v z incidentedges(v) - returns an enumeration of the edges incident upon v z endvertices(e) - return an array of size 2 storing the end vertices of e

Directed Edges z Directededges() - return an enumeration of all directed edges z indegree(v) - return the indegree of v z outdegree(v) - return the outdegree of v z origin (v) - return the origin of directed edge e z other functions - inadjacentvertices(), outadjacentvertices(), destination()

Updating Graphs z Insertedge(v, w, o) - insert and return an undirected edge between vertices v and w storing the object o at this position z Insertvertex(o) - insert and return a new vertex storing the object o at this position z removevertex (v) - remove the vertex v and all incident edges z removeedge(e) - remove edge e

Implementation of a graph data structure

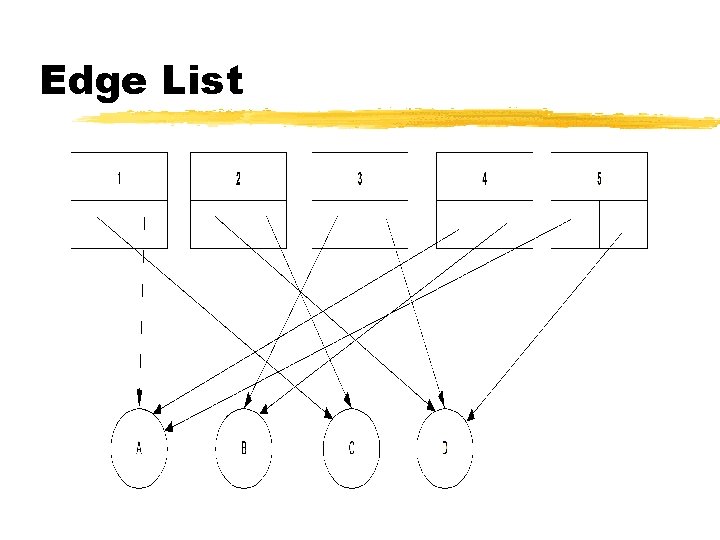
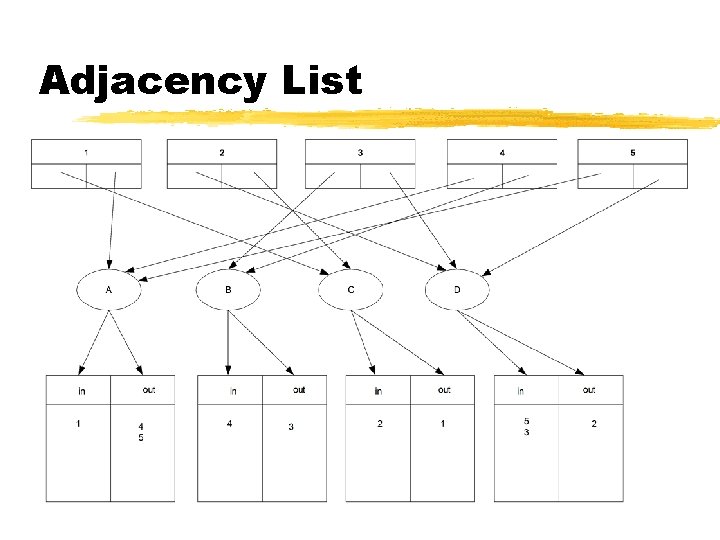
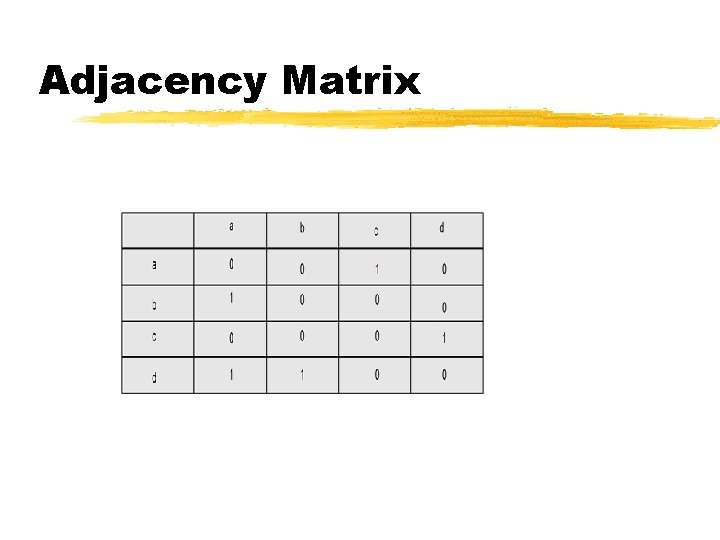
Graph Implementations z. Edge List Õvertices and edges are nodes Õedge nodes refer to incident vertex nodes z. Adjacency List Õsame as edge list but vertex nodes also refer to incident edge nodes z. Adjacency Matrix Õ 2 D matrix of vertices; entries are edges

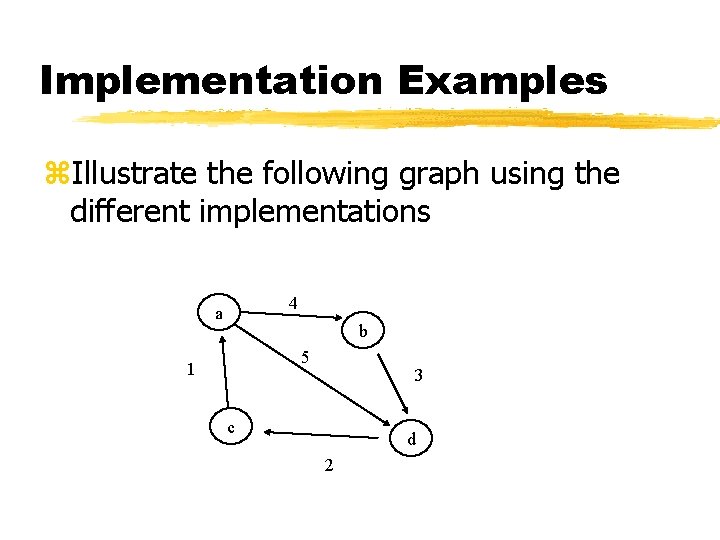
Implementation Examples z. Illustrate the following graph using the different implementations 4 a b 5 1 3 c d 2

Edge List

Adjacency List

Adjacency Matrix

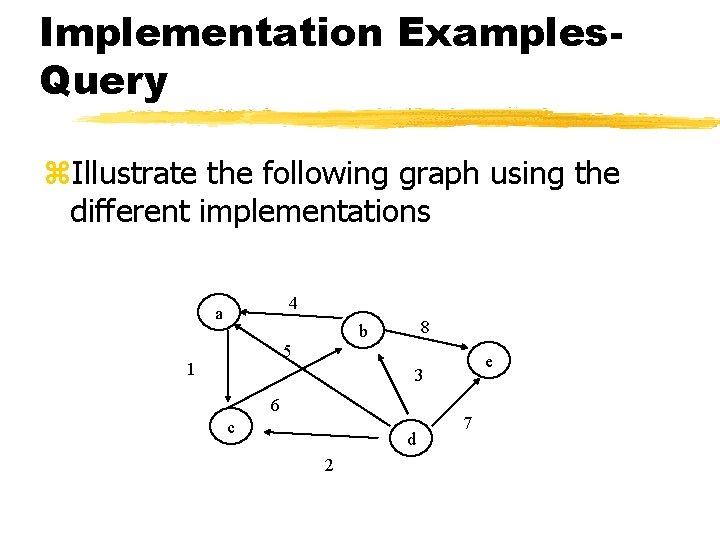
Implementation Examples. Query z. Illustrate the following graph using the different implementations 4 a 8 b 5 1 e 3 6 c d 2 7

Comparing Implementations z. Edge List Õsimplest but most inefficient z. Adjacency List Õmany vertex operations are O(d) time where d is the degree of the vertex z. Adjacency Matrix Õadjacency test is O(1) Õaddition/removal of a vertex: resize 2 D array

Graph Traversals z Traversal - A systematic procedure for exploring a graph by examining all of its vertices and edges z Consistency - rules to determine the order of visits (topdown, alphabetical, etc. ) - make the path consistent with the actual graph (don’t change conventions)

Graph Traversals z. Depth First Search (DFS) Õvisit a starting vertex s Õrecursively visit unvisited adjacent vertices z. Breadth First Search (BFS) Õvisit starting vertex s Õvisit unvisited vertices adjacent to s, then visit unvisited vertices adjacent to them, and so on … (visit by levels)

DFS Traversal z Depth First Search - recursively visit (traverse) unvisited vertices z Dead End - reaching a vertex where all the incident edges go to a previously visited vertex z Back Track - If a dead-end vertex is reached, go to the previous vertex

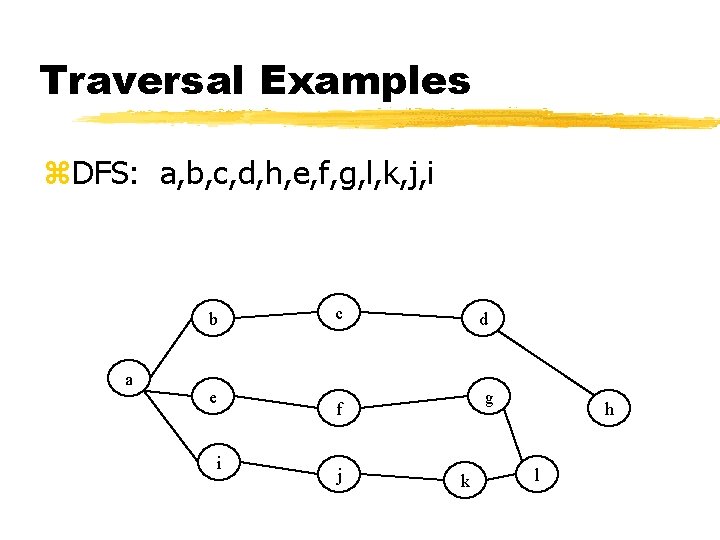
Traversal Examples z. DFS: a, b, c, d, h, e, f, g, l, k, j, i b a e i c d g f j k h l

DFS Traversal z Path of the DFS traversal - path=a, b, c, d, h - h is a dead end vertex - back track to d, c, b, a and go to another adjacent (unvisited) vertex -> e - path=a, e, f, g, k, j, i - i is a dead end vertex - back track to all the way back to a (also a dead end vertex) z finished

BFS Traversal z. Visit adjacent vertices by levels zdiscovery edges - edges that lead to an unvisited vertex zcross edge - edges that lead to a previously visited vertex

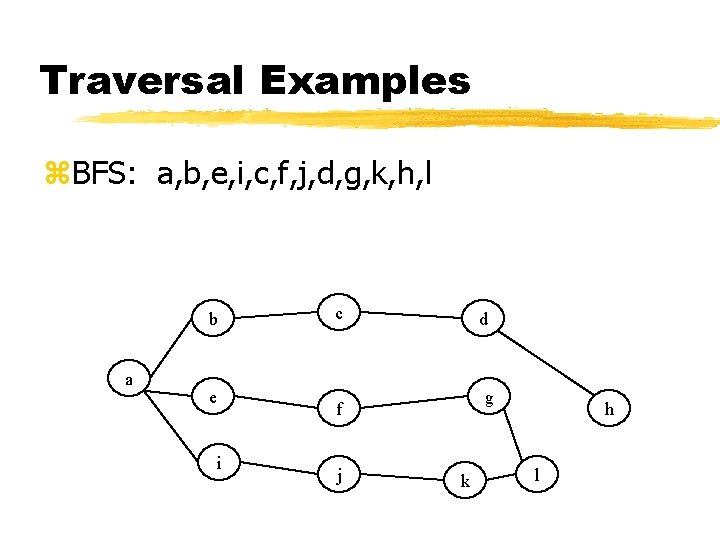
Traversal Examples z. BFS: a, b, e, i, c, f, j, d, g, k, h, l b a e i c d g f j k h l

DFS Algorithm DFS(v) Input: Vertex v Output: Depends on the application mark v as visited; perform processing for each vertex w adjacent to v do if w is unmarked then DFS(w)

BFS Algorithm BFS(s) Input: Starting vertex s Output: Depends on the application // traversal algorithm uses a queue Q // loop terminates when Q is empty

BFS Algorithm continued Q new Queue() mark s as visited and Q. enqueue(s) while not Q. is. Empty() v Q. dequeue() perform processing on v for each vertex w adjacent to v do if w is unmarked then mark w as visited and Q. enqueue(w)

Query z Let G be a graph whose vertices are the integers 1 through 8 and let the adjacent vertices of each vertex be given by the table below : Vertex Adjacent Vertices 1 (2, 3, 4) 2 (1, 3, 4) 3 (1, 2, 4) 4 (1, 2, 3, 6) 5 (6, 7, 8) 6 (4, 5, 7) 7 (5, 6, 8) 8 (5, 7)

Query z Assume that in the traversal of G, the adjacent vertices of a given vertex are returned in the same order as they are listed in the above table: a) Draw G b) Give the sequence of vertices of G visited using a DFS traversal order starting at vertex 1 c) Give the sequence of vertices visited using a BFS traversal starting at vertex 1

Weighted Graphs Overview

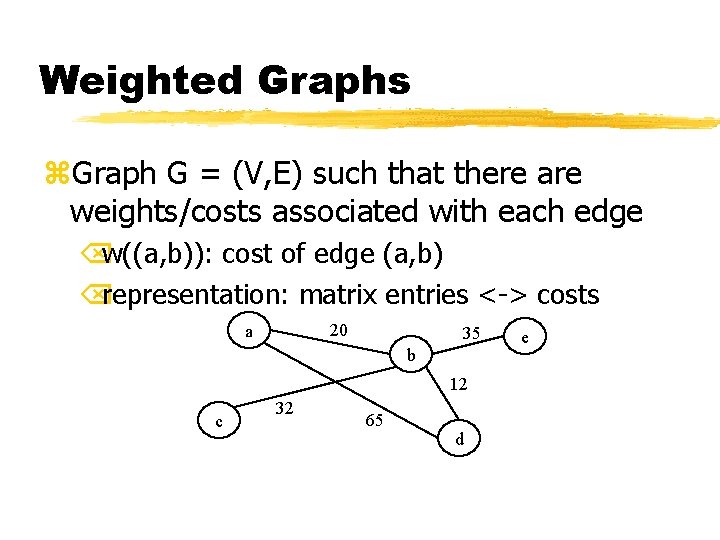
Weighted Graphs z. Graph G = (V, E) such that there are weights/costs associated with each edge Õw((a, b)): cost of edge (a, b) Õrepresentation: matrix entries <-> costs 20 a 35 b 12 c 32 65 d e

Problems on Weighted Graphs z. Minimum-cost Spanning Tree ÕGiven a weighted graph G, determine a spanning tree with minimum total edge cost z. Single-source shortest paths ÕGiven a weighted graph G and a source vertex v in G, determine the shortest paths from v to all other vertices in G ÕPath length: sum of all edges in path

Weighted Graphs-Concerns z. Minimum Cost z. Shortest Path

Weighted Graphs z. Shortest Path - Dijkstra’s Algorithm z. Minimum Spanning Trees - Kruskal’s Algorithm