GRAPHS Definition A graph is an abstract data

GRAPHS

Definition A graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from mathematics. A graph data structure consists of a finite (and possibly mutable) set of vertices or nodes or points, together with a set of unordered pairs of these vertices for an undirected graph or a set of ordered pairs for a directed graph. These pairs are known as edges, arcs, or lines for an undirected graph and as arrows, directed edges, directed arcs, or directed lines for a directed graph. The vertices may be part of the graph structure, or may be external entities represented by integer indices or references.
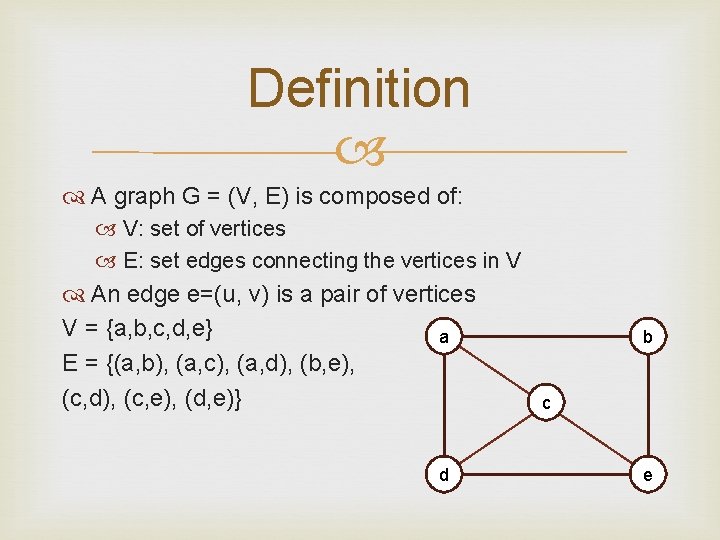
Definition A graph G = (V, E) is composed of: V: set of vertices E: set edges connecting the vertices in V An edge e=(u, v) is a pair of vertices V = {a, b, c, d, e} a E = {(a, b), (a, c), (a, d), (b, e), (c, d), (c, e), (d, e)} d b c e

Applications Electric circuits Networks Roads Flights Communications

Basic Operations Basic primary operations of a Graph − Add Vertex − Adds a vertex to the graph. Add Edge − Adds an edge between the two vertices of the graph. Display Vertex − Displays a vertex of the graph.

Graph Representations Graphs are represented using following representations: Adjacency Matrix Incidence Matrix Adjacency List
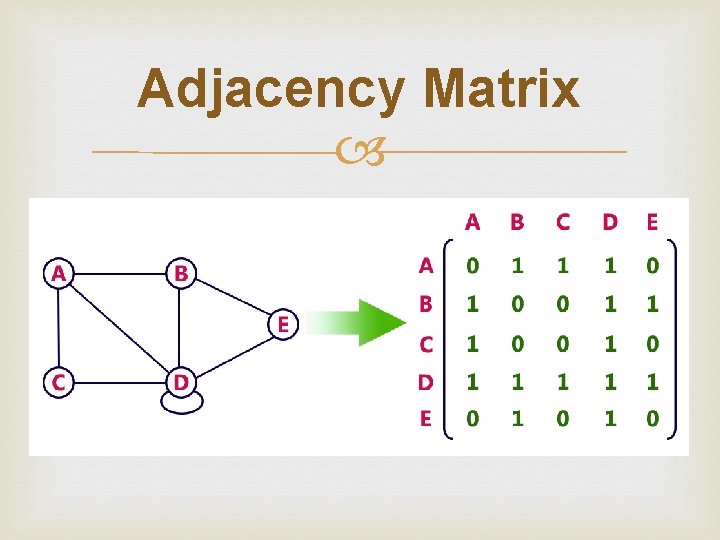
Adjacency Matrix
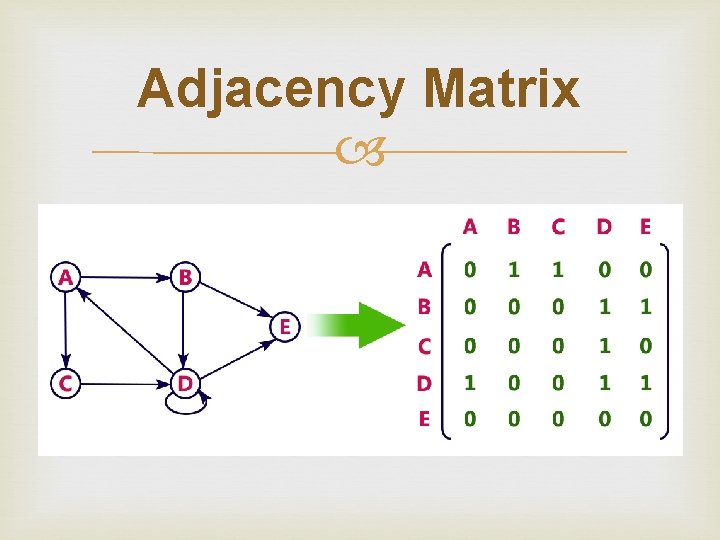
Adjacency Matrix
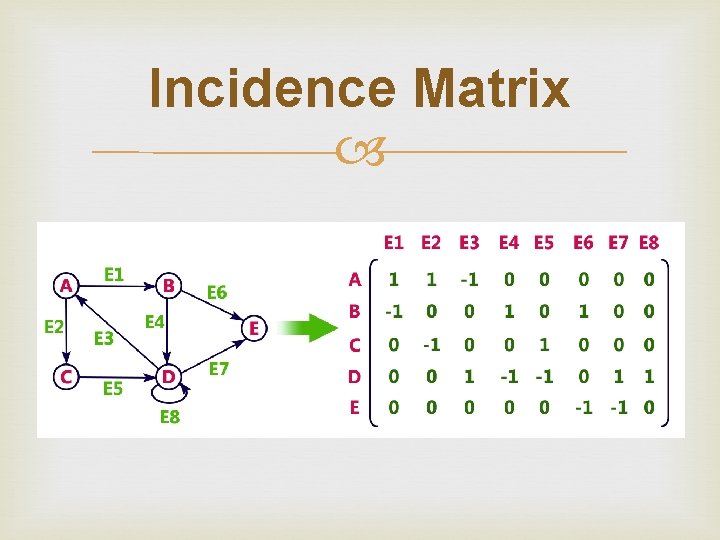
Incidence Matrix
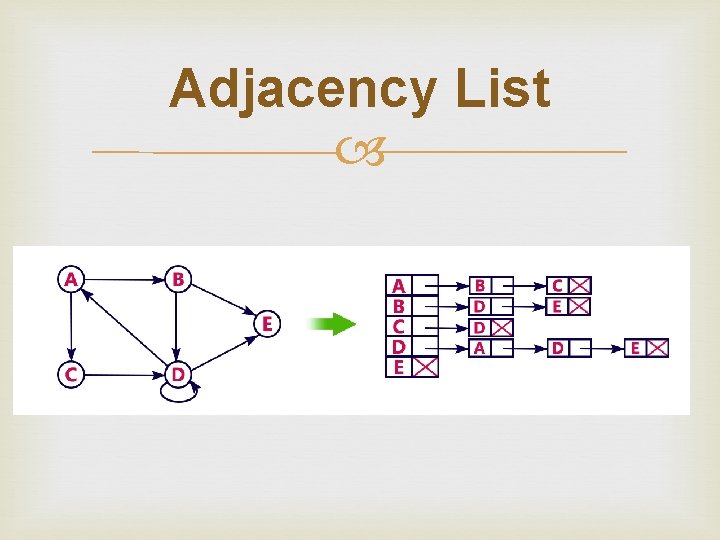
Adjacency List

Adjacent and Incident If (v 0, v 1) is an edge in an undirected graph, v 0 and v 1 are adjacent The edge (v 0, v 1) is incident on vertices v 0 and v 1 If < v 0, v 1 > is an edge in a directed graph v 0 is adjacent to v 1, and v 1 is adjacent from v 0 The edge < v 0, v 1 > is incident on v 0 and v 1

Degree of Vertex
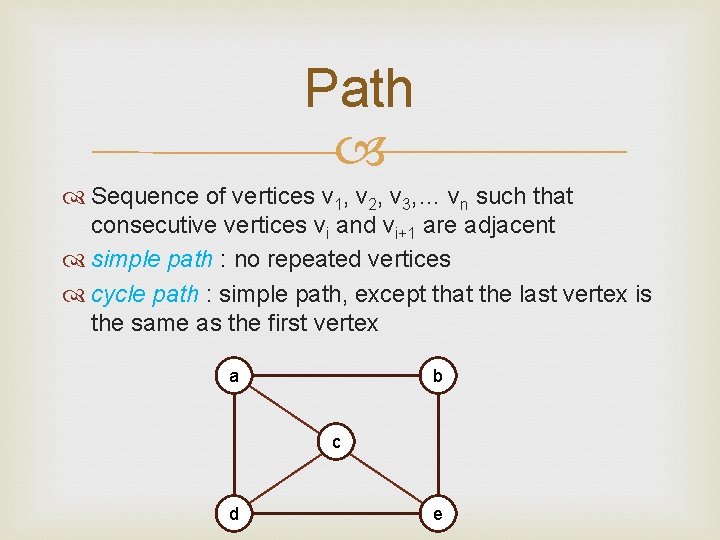
Path Sequence of vertices v 1, v 2, v 3, … vn such that consecutive vertices vi and vi+1 are adjacent simple path : no repeated vertices cycle path : simple path, except that the last vertex is the same as the first vertex a b c d e

Graph types connected graph : any two vertices are connected by some path sub graph : subset of vertices and edges forming a graph connected component : maximal connected subgraph tree : connected graph without cycles forest : collection of trees

Connectivity Let n = # of vertices and m = # of edges A complete graph one in which all pairs of vertices are adjacent Each of n vertices incident to n-1 edges, however each edge counted twice. Therefore m=n(n-1)/2 If a graph is not complete m<n(n-1)/2 If m<n-1 Graph is not connected

Directed vs. Undirected An undirected graph is one which the pair of vertices are not ordered, (v 0, v 1)=(v 1, v 0) A directed graph is one which each edge is a directed pair of vertices, < v 0, v 1 > != < v 1, v 0 >
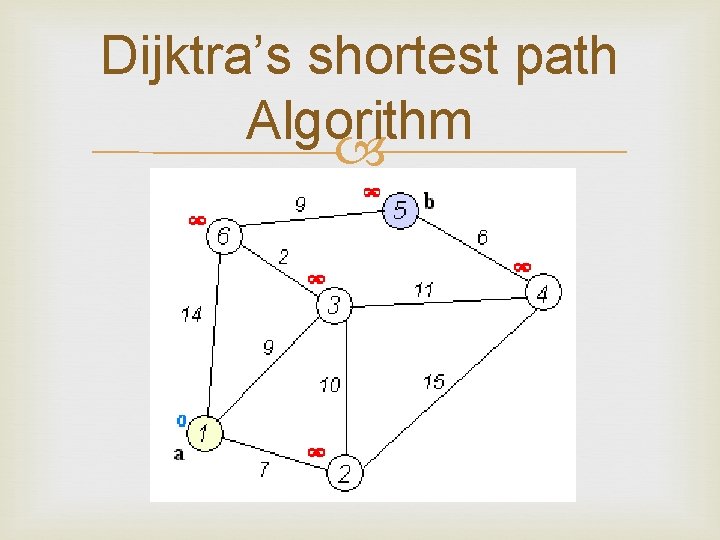
Dijktra’s shortest path Algorithm

Dijktra’s algorithm between 2 nodes

Dijkstra’s algorithm based on Euclidean distance
- Slides: 19