Graphs David Johnson Describing the Environment How do

Graphs David Johnson

Describing the Environment • How do you tell a person/robot how to get somewhere? – Tell me how to get to the student services building…

World Representation • Landmarks • Paths/Roads • Map • This is abstracted as a graph – Not in the sense of a plot

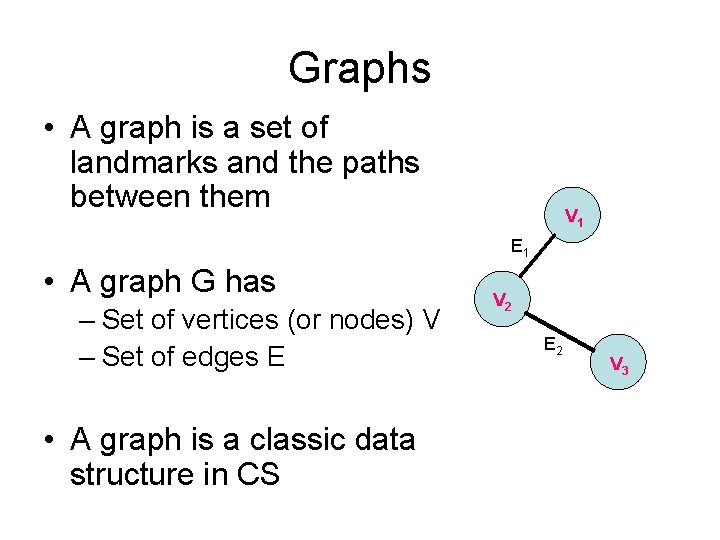
Graphs • A graph is a set of landmarks and the paths between them V 1 E 1 • A graph G has – Set of vertices (or nodes) V – Set of edges E • A graph is a classic data structure in CS V 2 E 2 V 3

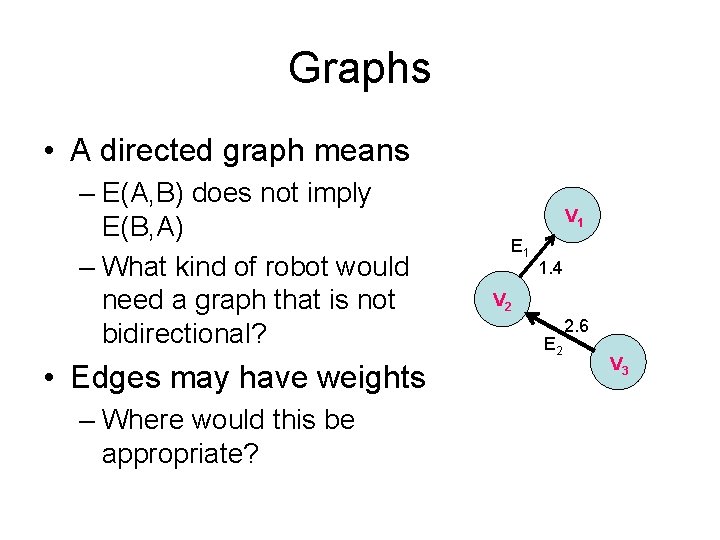
Graphs • A directed graph means – E(A, B) does not imply E(B, A) – What kind of robot would need a graph that is not bidirectional? • Edges may have weights – Where would this be appropriate? V 1 E 1 1. 4 V 2 E 2 2. 6 V 3

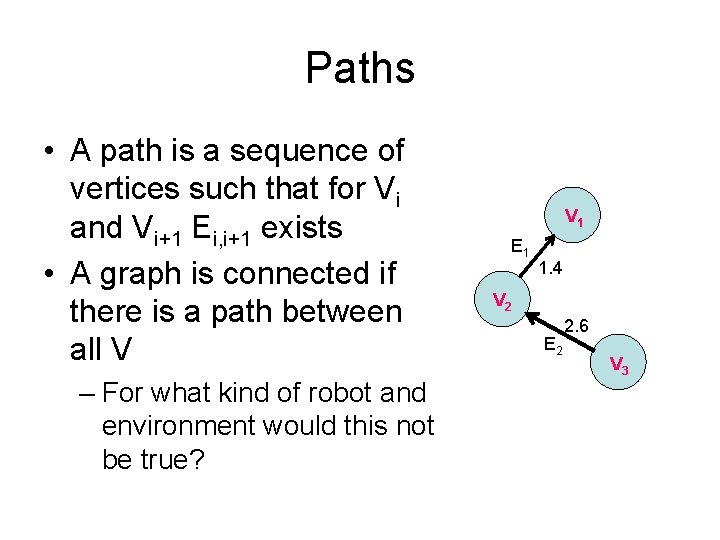
Paths • A path is a sequence of vertices such that for Vi and Vi+1 Ei, i+1 exists • A graph is connected if there is a path between all V – For what kind of robot and environment would this not be true? V 1 E 1 1. 4 V 2 E 2 2. 6 V 3

Imagine a simple robot • What is the simplest kind of robot you can think of?

Point Robots • A point robot can move along the infinitesimal width edges of a graph. • Path planning for this simple case is just searching a graph for a path.

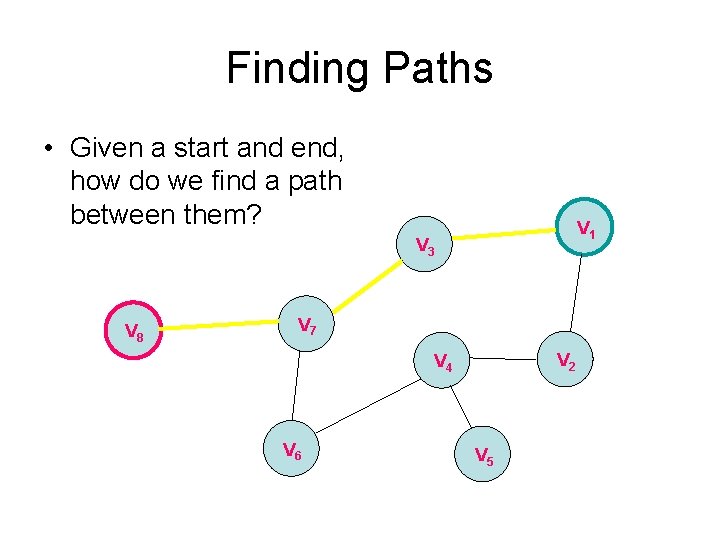
Finding Paths • Given a start and end, how do we find a path between them? V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

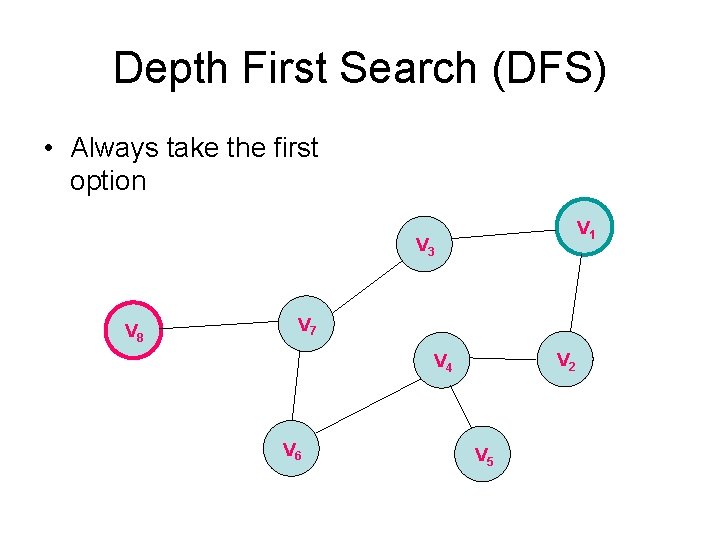
Depth First Search (DFS) • Always take the first option V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

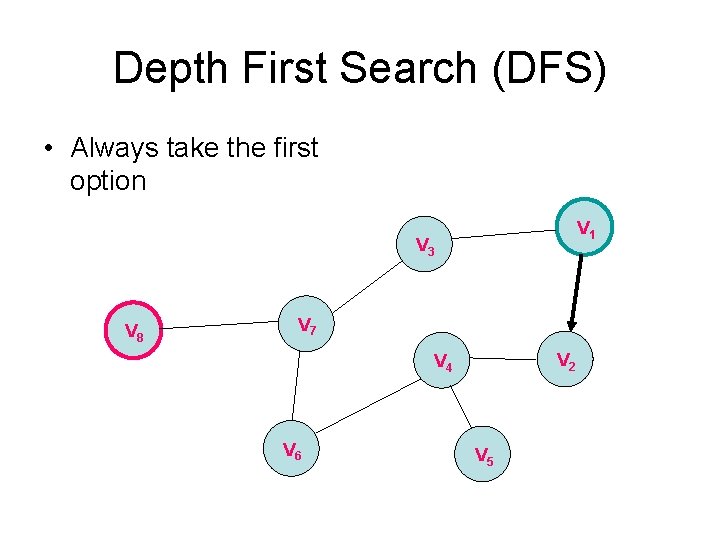
Depth First Search (DFS) • Always take the first option V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

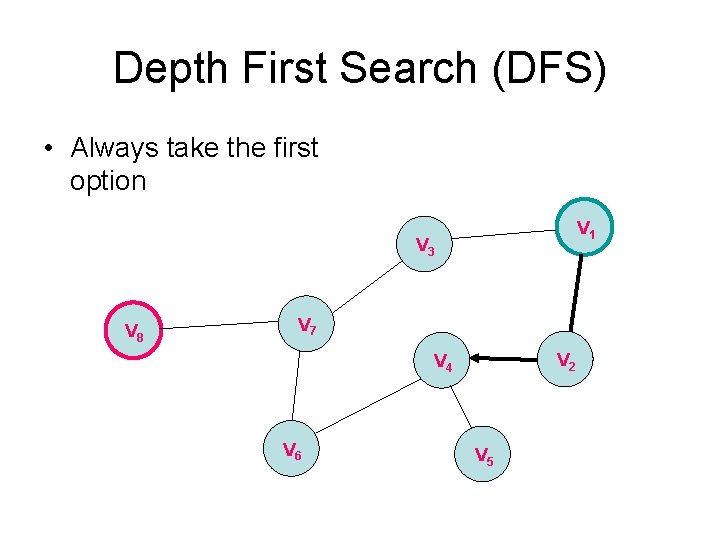
Depth First Search (DFS) • Always take the first option V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

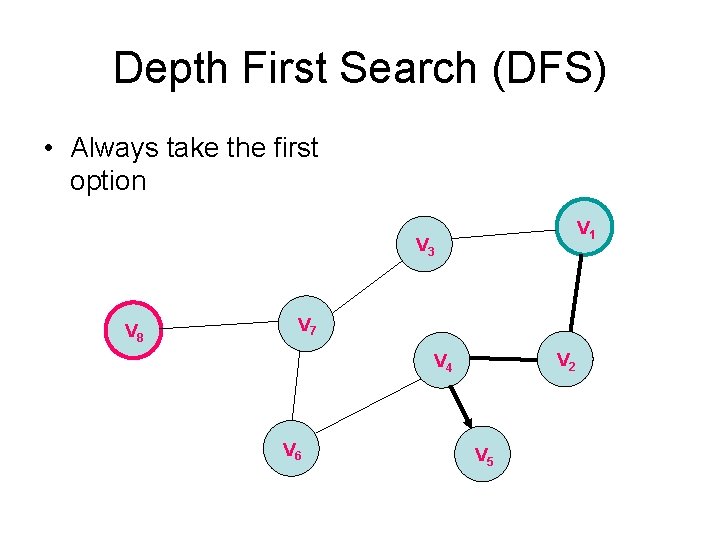
Depth First Search (DFS) • Always take the first option V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

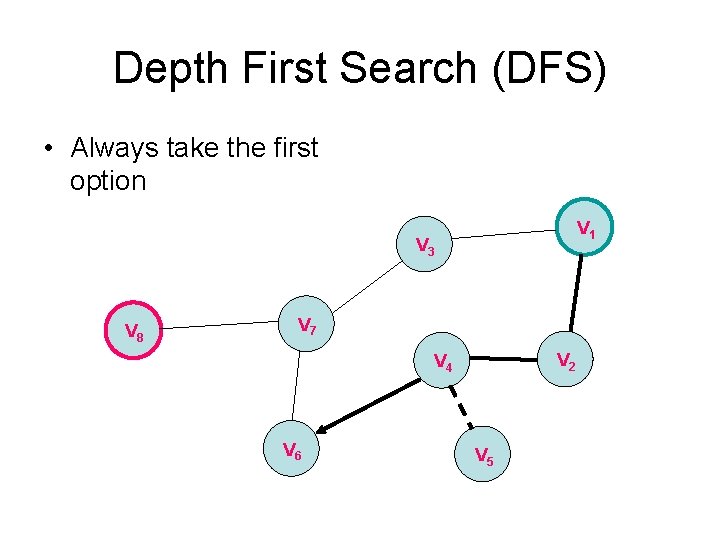
Depth First Search (DFS) • Always take the first option V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

Depth First Search (DFS) • Always take the first option V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

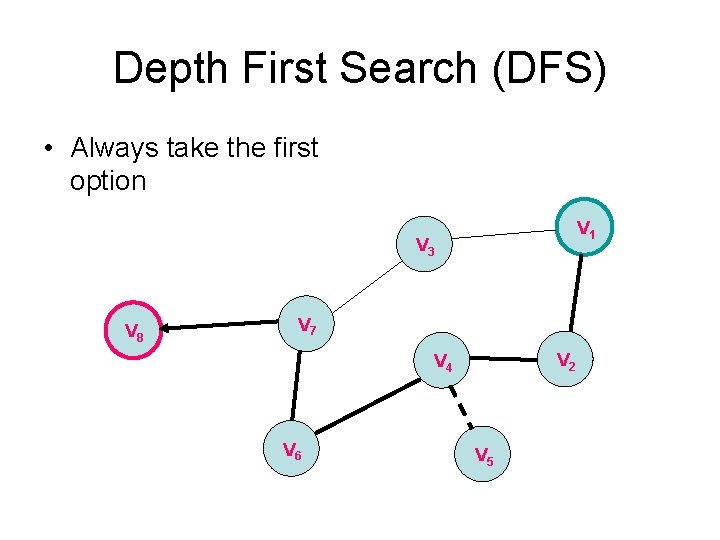
Depth First Search (DFS) • Always take the first option V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

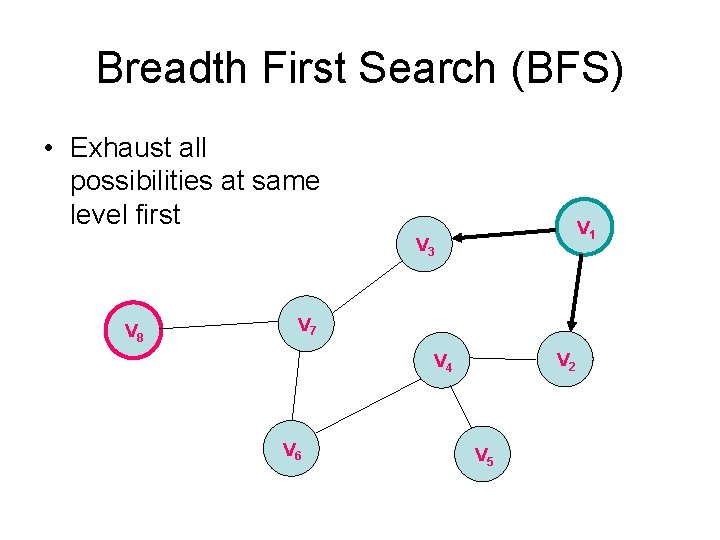
Breadth First Search (BFS) • Exhaust all possibilities at same level first V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

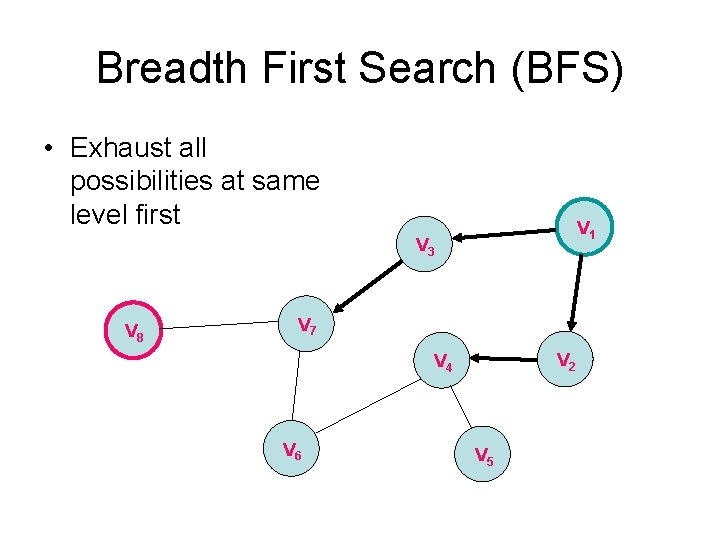
Breadth First Search (BFS) • Exhaust all possibilities at same level first V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

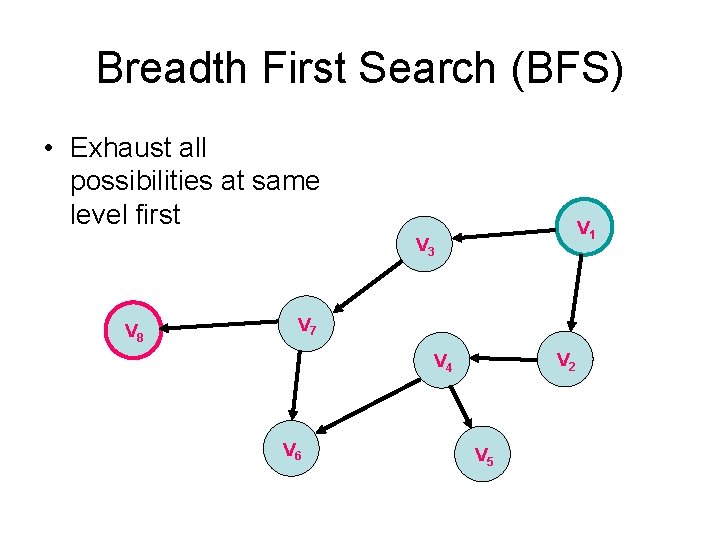
Breadth First Search (BFS) • Exhaust all possibilities at same level first V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

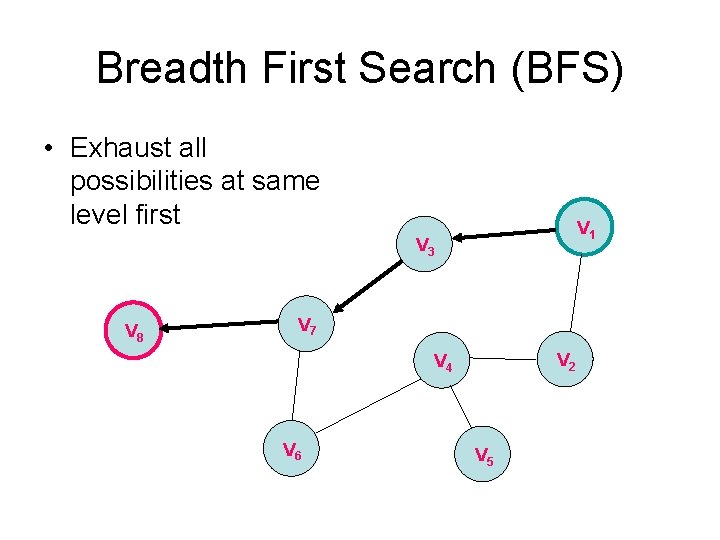
Breadth First Search (BFS) • Exhaust all possibilities at same level first V 1 V 3 V 8 V 7 V 2 V 4 V 6 V 5

Representing a graph in Matlab • Demo

Wavefront planner • Use BFS on a grid • Label cells with values – Start with zero – Expand from start – Add +1 to neighbors of current wavefront – Use gradient descent to search from goal to start

Representations: A Grid • Distance is reduced to discrete steps – For simplicity, we’ll assume distance is uniform • Direction is now limited from one adjacent cell to another

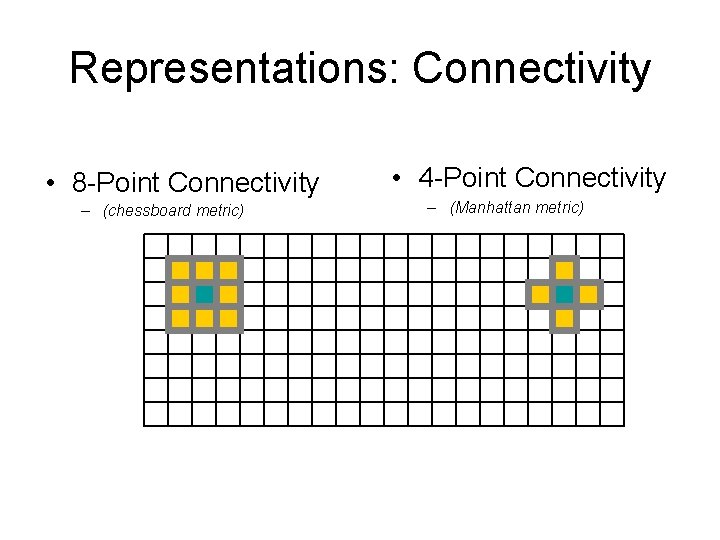
Representations: Connectivity • 8 -Point Connectivity – (chessboard metric) • 4 -Point Connectivity – (Manhattan metric)

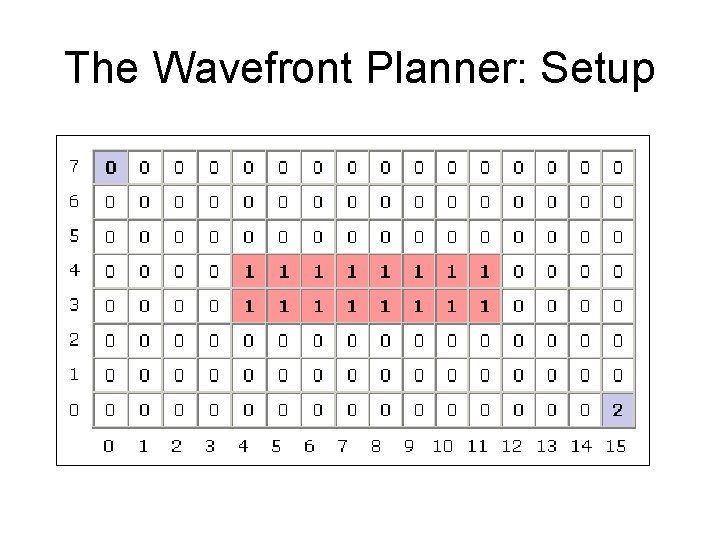
The Wavefront Planner: Setup

The Wavefront in Action (Part 1) • Starting with the goal, set all adjacent cells with “ 0” to the current cell + 1 – 4 -Point Connectivity or 8 -Point Connectivity? – Your Choice. We’ll use 8 -Point Connectivity in our example

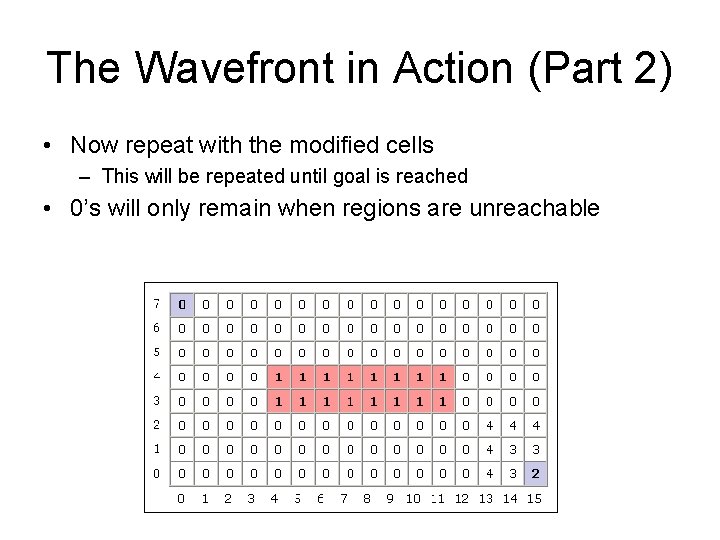
The Wavefront in Action (Part 2) • Now repeat with the modified cells – This will be repeated until goal is reached • 0’s will only remain when regions are unreachable

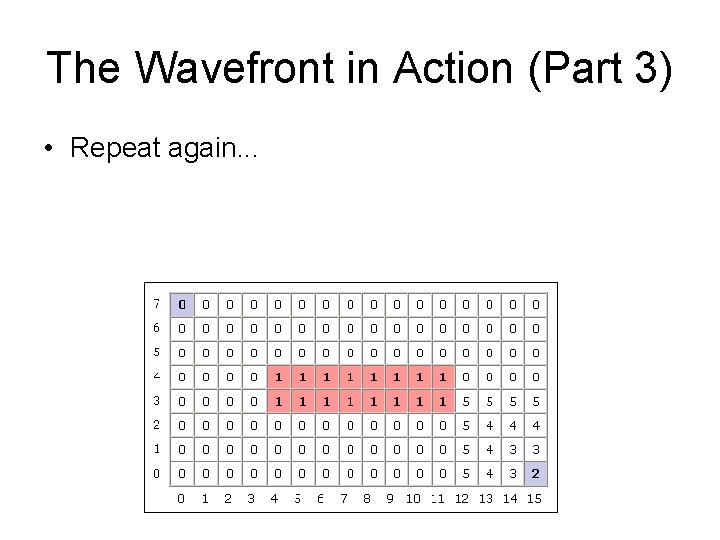
The Wavefront in Action (Part 3) • Repeat again. . .

The Wavefront in Action (Part 4) • And again. . .

The Wavefront in Action (Part 5) • And again until. . .

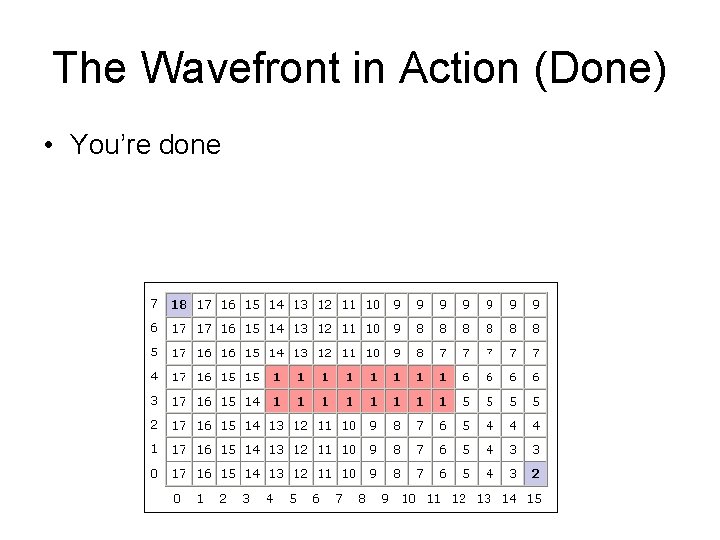
The Wavefront in Action (Done) • You’re done

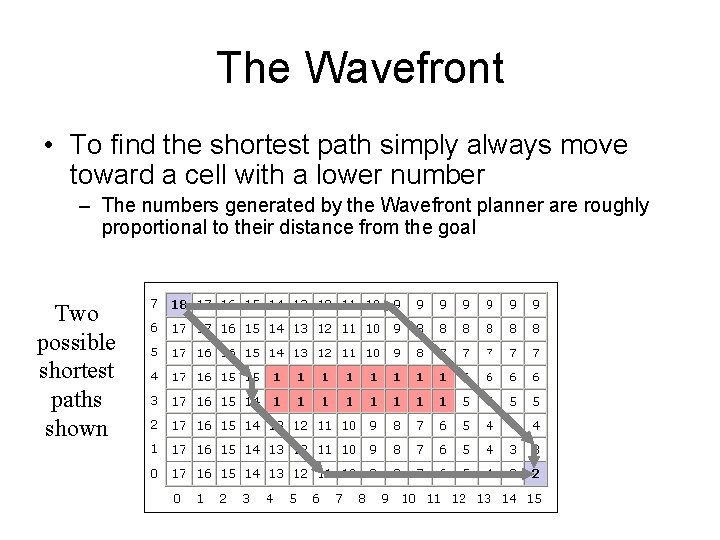
The Wavefront • To find the shortest path simply always move toward a cell with a lower number – The numbers generated by the Wavefront planner are roughly proportional to their distance from the goal Two possible shortest paths shown