Graphs CS240341 Uses for Graphs computer networks and










- Slides: 15

Graphs CS-240/341

Uses for Graphs • • • computer networks and routing airline flights geographic maps course prerequisite structures tasks for completing a job plumbing/hydraulic systems electrical circuits automatons/finite state machines grammar mappings

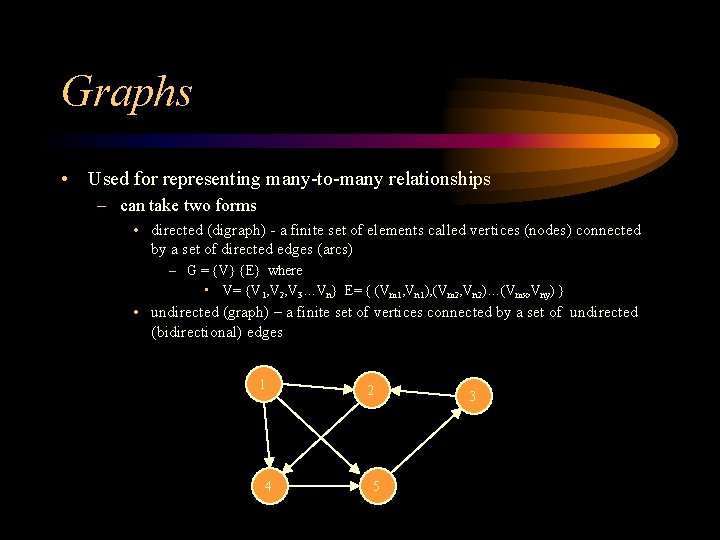
Graphs • Used for representing many-to-many relationships – can take two forms • directed (digraph) - a finite set of elements called vertices (nodes) connected by a set of directed edges (arcs) – G = {V} {E} where • V= {V 1, V 2, V 3…Vn} E= { (Vm 1, Vn 1), (Vm 2, Vn 2)…(Vmx, Vny) } • undirected (graph) – a finite set of vertices connected by a set of undirected (bidirectional) edges 1 4 2 5 3

Edges • Represent a relationship between two vertices – to ; in a digraph represents that A is adjacent to B A B 25 – from ; in a digraph B is adjacent from A – in an undirected graph an edge merely represents that the vertices are adjacent • Edges may also have an associated weight or value – if the vertices represent cities then the edge may represent a connection (road) between them and the weight may represent the distance and the direction may represent a one way street – if the graph represents a network of active components (p-n junctions, diodes/transistors) then the direction represents the direction of the pn junctions and the edges represent the way the components are connected and the weights represent the forward resistance of the junction (backward resistance is infinity)

Digraph Abstract Data Type • Data Elements: – collection of vertices and a collection of edges and weights • Basic Operations: – – – – Create an empty digraph Check if the digraph is empty Destroy a digraph Insert a new vertex Insert a new edge between two existing vertices Delete a vertex and all directed edges to or from it Delete a directed edge between to vertices search for an edge value

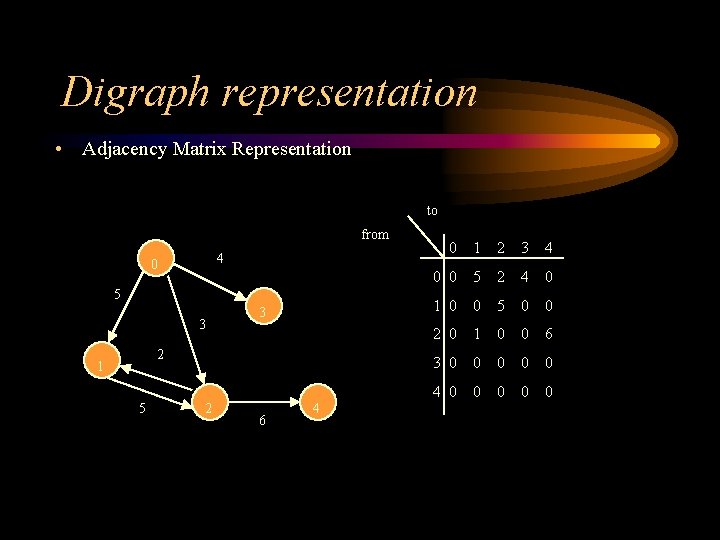
Digraph representation • Adjacency Matrix Representation to from 4 0 5 3 3 2 1 5 2 6 4 0 1 2 3 4 0 0 5 2 4 0 1 0 0 5 0 0 2 0 1 0 0 6 3 0 0 0 4 0 0 0

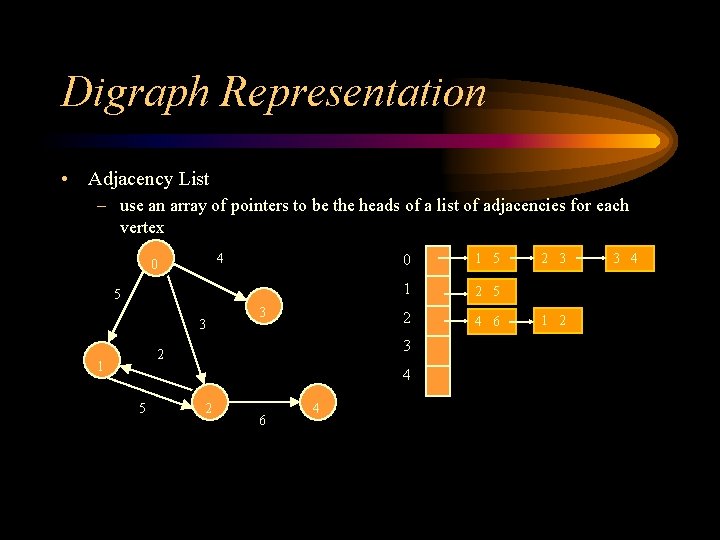
Digraph Representation • Adjacency List – use an array of pointers to be the heads of a list of adjacencies for each vertex 4 0 5 3 3 1 5 1 2 5 2 4 6 3 2 1 0 4 5 2 6 4 2 3 1 2 3 4

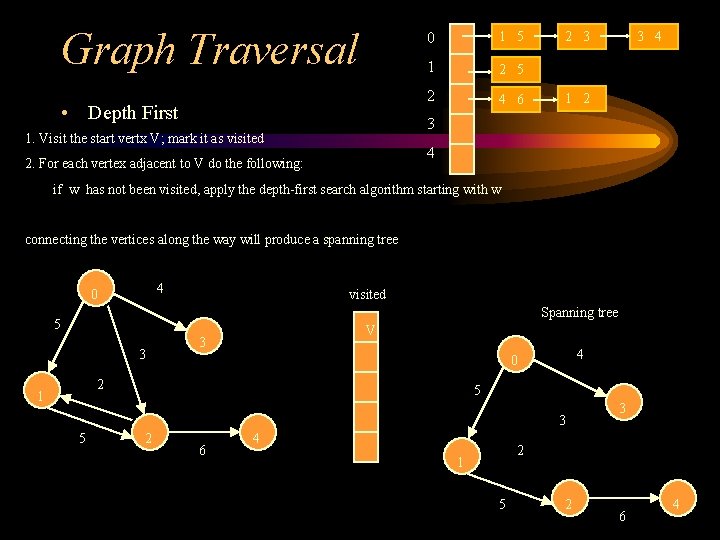
Graph Traversal • Depth First 0 1 5 1 2 5 2 4 6 2 3 3 4 1 2 3 1. Visit the start vertx V; mark it as visited 4 2. For each vertex adjacent to V do the following: if w has not been visited, apply the depth-first search algorithm starting with w connecting the vertices along the way will produce a spanning tree 4 0 visited Spanning tree 5 3 V 3 2 1 4 0 5 3 5 2 6 4 3 2 1 5 2 6 4

Graph Traversal • Breadth First 1. Visit the start vertex V 2. Initialize a queue to contain only the start vertex 3. While the queue is not empty do the following Rempve vertex V from the queue For all vertices w adjacent to v do the following: If w has not been visited then Visit W Add W to the queue

Spanning Trees • The set of vertices and edges produced by a DFS traversal produces what is known as a spanning tree – if the DFS doesn’t include all of the vertices, then do another DFS starting at a vertex not yet in the tree. This may have to be done a number of times but will eventually produce a set disjoint (not connected) spanning trees called a spanning forest.

Degree of a vertex • Digraph – In degree is the number of edges coming into a vertex – Out degree is the number of edges going out of a vertex • Undirected Graph – degree is the number of edges touching a vertex – the highest degree of any vertex is the degree of the graph In degree = 3 3 Out degree = 2

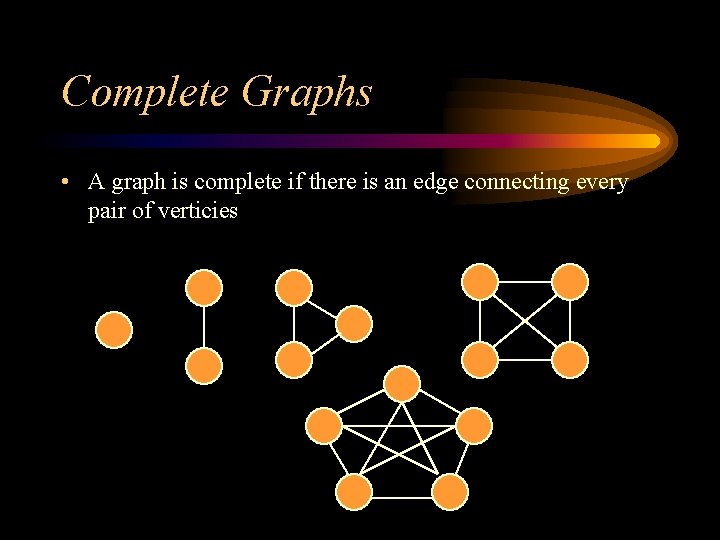
Complete Graphs • A graph is complete if there is an edge connecting every pair of verticies

Trees • A tree is a special case of a graph – a binary tree is an order 2 graph • If a tree is represented by its adjacencies (matrix or list) it can be traversed BFS or DFS • A BFS done starting at the root should yield the same traversal path as a preorder tree traversal

Connectedness • A graph is said to be connected if there is a path from every node to every other node – do a DFS starting at each vertex – that vertex is complete is the visited array is full • vertices not visited are not connected

NP-Complete Problems • NP - nondeterministic polynomial – cannot be solved in polynomial time – use a heuristic solution • guess an answer (nondeterministic) , try to prove it wrong, if you can’t prove it wrong it must be part of the solution set • P – deterministic polynomial