Graphs Chapters 10 1 and 10 2 Based

Graphs Chapters 10. 1 and 10. 2 Based on slides by Y. Peng University of Maryland 1

Introduction to Graphs Definition: A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. For each e E, e = {u, v} where u, v V. An undirected graph (not simple) may contain loops. An edge e is a loop if e = {u, u} for some u V. 2

Introduction to Graphs Definition: A directed graph G = (V, E) consists of a set V of vertices and a set E of edges that are ordered pairs of elements in V. For each e E, e = (u, v) where u, v V. An edge e is a loop if e = (u, u) for some u V. A simple graph is just like a directed graph, but with no specified direction of its edges. 3
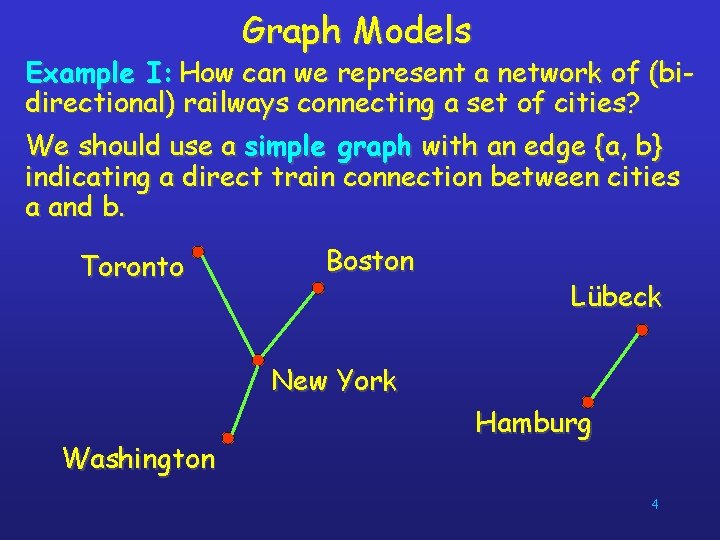
Graph Models Example I: How can we represent a network of (bidirectional) railways connecting a set of cities? We should use a simple graph with an edge {a, b} indicating a direct train connection between cities a and b. Toronto Boston Lübeck New York Washington Hamburg 4
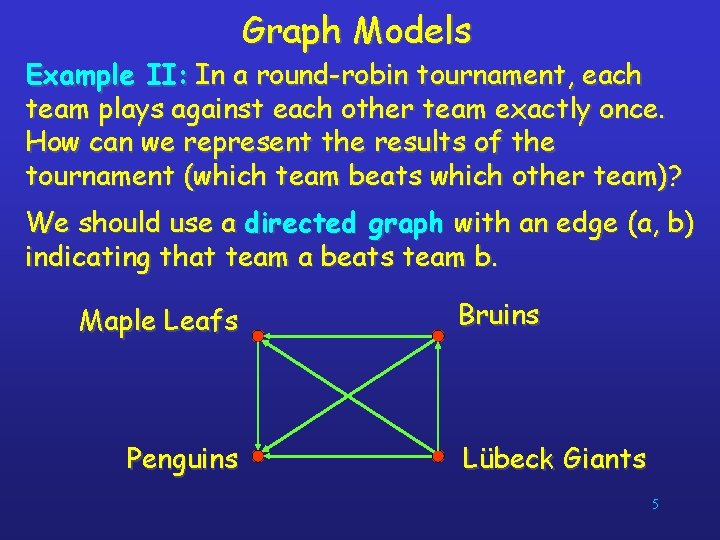
Graph Models Example II: In a round-robin tournament, each team plays against each other team exactly once. How can we represent the results of the tournament (which team beats which other team)? We should use a directed graph with an edge (a, b) indicating that team a beats team b. Maple Leafs Penguins Bruins Lübeck Giants 5

Graph Terminology Definition: Two vertices u and v in an undirected graph G are called adjacent (or neighbors ) in G if {u, v} is an edge in G. If e = {u, v}, the edge e is called incident with the vertices u and v. The edge e is also said to connect u and v. The vertices u and v are called endpoints of the edge {u, v}. 6

Graph Terminology Definition: The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex. In other words, you can determine the degree of a vertex in a displayed graph by counting the lines that touch it. The degree of the vertex v is denoted by deg(v). 7

Graph Terminology A vertex of degree 0 is called isolated , since it is not adjacent to any vertex. Note: A vertex with a loop at it has at least degree 2 and, by definition, is not isolated , even if it is not adjacent to any other vertex. A vertex of degree 1 is called pendant. It is adjacent to exactly one other vertex. 8
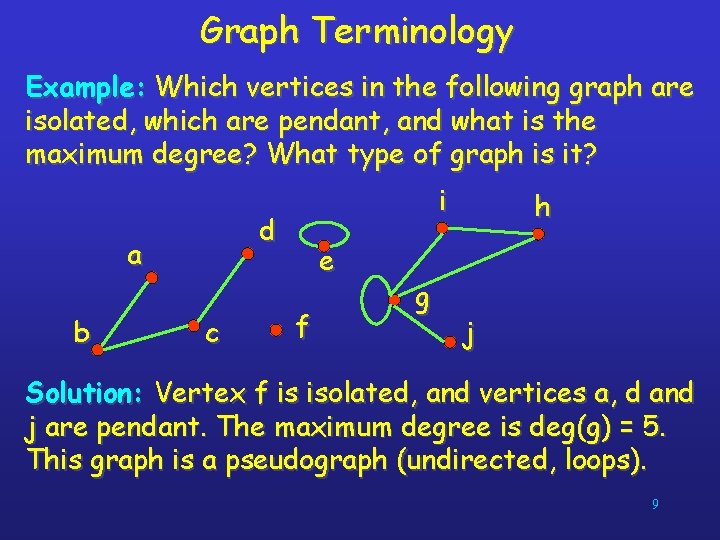
Graph Terminology Example: Which vertices in the following graph are isolated, which are pendant, and what is the maximum degree? What type of graph is it? d a b i c e f g h j Solution: Vertex f is isolated, and vertices a, d and j are pendant. The maximum degree is deg(g) = 5. This graph is a pseudograph (undirected, loops). 9
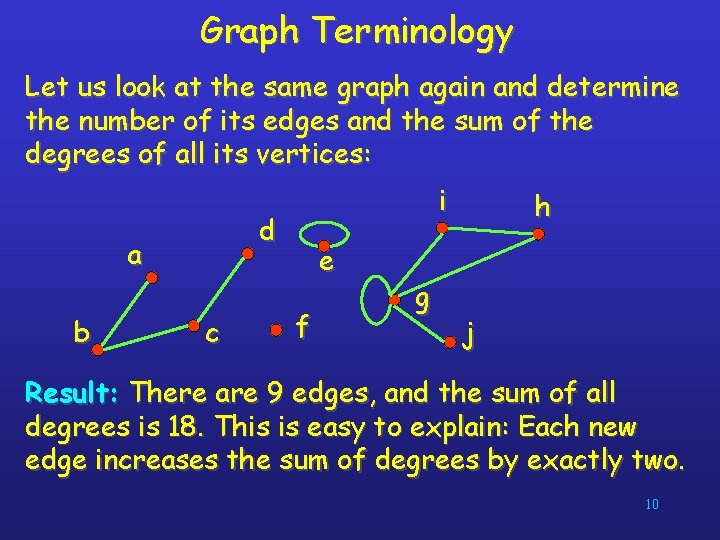
Graph Terminology Let us look at the same graph again and determine the number of its edges and the sum of the degrees of all its vertices: d a b i c e f g h j Result: There are 9 edges, and the sum of all degrees is 18. This is easy to explain: Each new edge increases the sum of degrees by exactly two. 10

Graph Terminology The Handshaking Theorem: Let G = (V, E) be an undirected graph with e edges. Then 2 e = v V deg(v) Example: How many edges are there in a graph with 10 vertices, each of degree 6? Solution: The sum of the degrees of the vertices is 6 10 = 60. According to the Handshaking Theorem, it follows that 2 e = 60, so there are 30 edges. 11

Graph Terminology Theorem: An undirected graph has an even number of vertices of odd degree. Proof: Let V 1 and V 2 be the set of vertices of even and odd degrees, respectively (Thus V 1 V 2 = , and V 1 V 2 = V). Then by Handshaking theorem 2|E| = v V deg(v) = v V 1 deg(v) + v V 2 deg(v) Since both 2|E| and v V 1 deg(v) are even, v V 2 deg(v) must be even. Since deg(v) if odd for all v V 2, |V 2| must be even. QED 12

Graph Terminology Definition: When (u, v) is an edge of the graph G with directed edges, u is said to be adjacent to v, and v is said to be adjacent from u. The vertex u is called the initial vertex of (u, v), and v is called the terminal vertex of (u, v). The initial vertex and terminal vertex of a loop are the same. 13

Graph Terminology Definition: In a graph with directed edges, the indegree of a vertex v, denoted by deg -(v) , is the number of edges with v as their terminal vertex. The out-degree of v, denoted by deg +(v) , is the number of edges with v as their initial vertex. Question: How does adding a loop to a vertex change the in-degree and out-degree of that vertex? Answer: It increases both the in-degree and the out-degree by one. 14

Graph Terminology Example: What are the in-degrees and out-degrees of the vertices a, b, c, d in this graph: deg-(a) = 1 deg+(a) = 2 deg-(d) = 2 deg+(d) = 1 a d b c deg-(b) = 4 deg+(b) = 2 deg-(c) = 0 deg+(c) = 2 15

Graph Terminology Theorem: Let G = (V, E) be a graph with directed edges. Then: v V deg-(v) = v V deg+(v) = |E| This is easy to see, because every new edge increases both the sum of in-degrees and the sum of out-degrees by one. 16
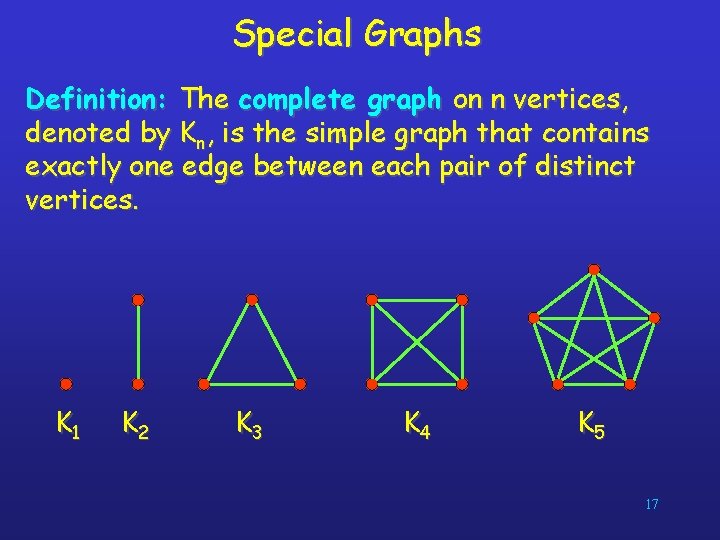
Special Graphs Definition: The complete graph on n vertices, denoted by Kn, is the simple graph that contains exactly one edge between each pair of distinct vertices. K 1 K 2 K 3 K 4 K 5 17
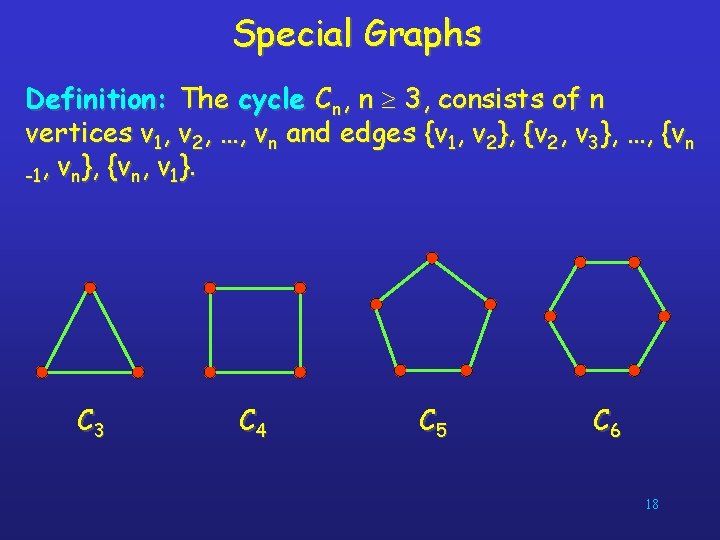
Special Graphs Definition: The cycle Cn, n 3, consists of n vertices v 1, v 2, …, vn and edges {v 1, v 2}, {v 2, v 3}, …, {vn -1, vn}, {vn, v 1}. C 3 C 4 C 5 C 6 18
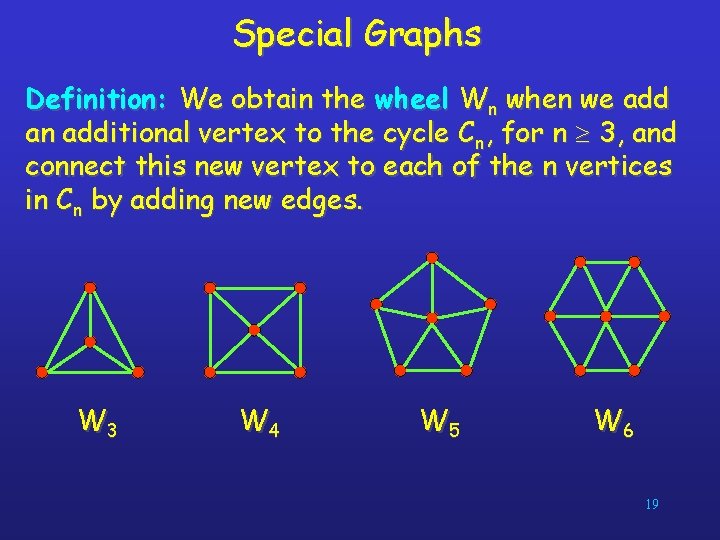
Special Graphs Definition: We obtain the wheel Wn when we add an additional vertex to the cycle Cn, for n 3, and connect this new vertex to each of the n vertices in Cn by adding new edges. W 3 W 4 W 5 W 6 19
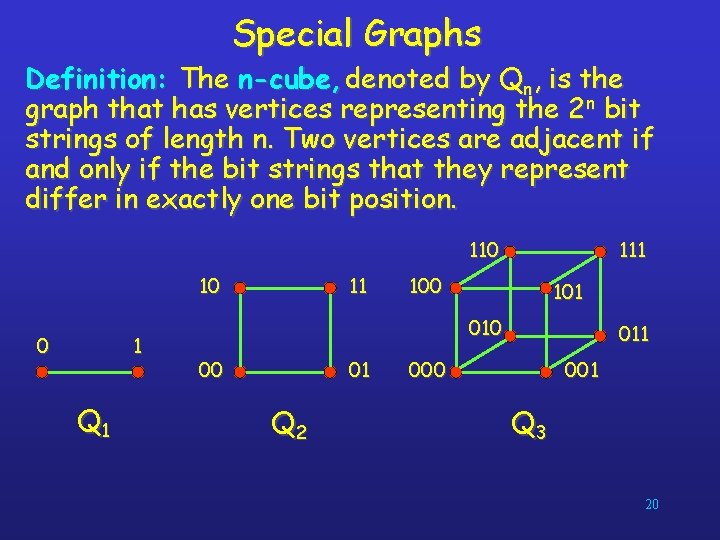
Special Graphs Definition: The n-cube, denoted by Qn, is the graph that has vertices representing the 2 n bit strings of length n. Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position. 110 10 0 1 Q 1 11 100 101 010 00 01 Q 2 011 000 001 Q 3 20

Special Graphs Definition: A simple graph is called bipartite if its vertex set V can be partitioned into two disjoint nonempty sets V 1 and V 2 such that every edge in the graph connects a vertex in V 1 with a vertex in V 2 (so that no edge in G connects either two vertices in V 1 or two vertices in V 2). For example, consider a graph that represents each person in a village by a vertex and each marriage by an edge. This graph is bipartite , because each edge connects a vertex in the subset of males with a vertex in the subset of females (if we think of traditional marriages). 21
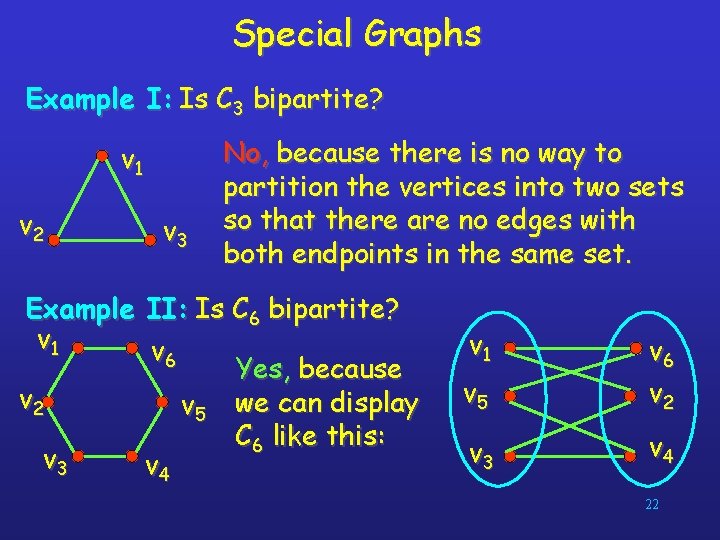
Special Graphs Example I: Is C 3 bipartite? v 1 v 2 v 3 No, because there is no way to partition the vertices into two sets so that there are no edges with both endpoints in the same set. Example II: Is C 6 bipartite? v 1 v 6 Yes, because v 2 v 5 we can display C 6 like this: v 3 v 4 v 1 v 5 v 6 v 2 v 3 v 4 22
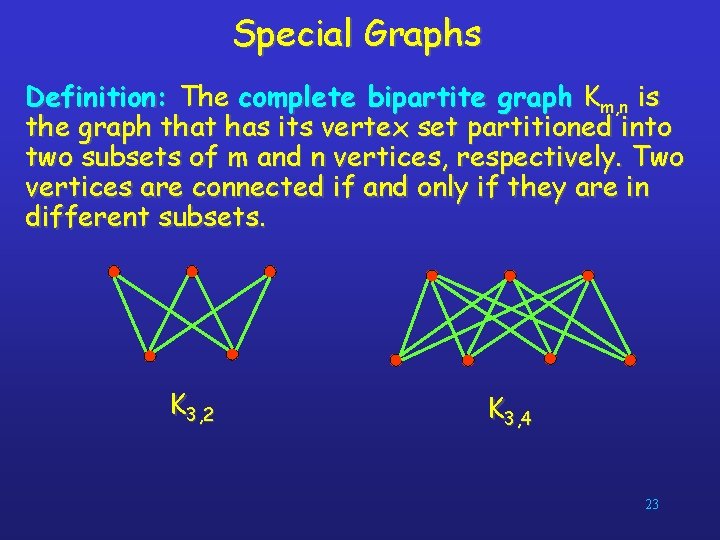
Special Graphs Definition: The complete bipartite graph Km, n is the graph that has its vertex set partitioned into two subsets of m and n vertices, respectively. Two vertices are connected if and only if they are in different subsets. K 3, 2 K 3, 4 23

Operations on Graphs Definition: A subgraph of a graph G = (V, E) is a graph H = (W, F) where W V and F E. Note: Of course, H is a valid graph, so we cannot remove any endpoints of remaining edges when creating H. Example: K 5 subgraph of K 5 24
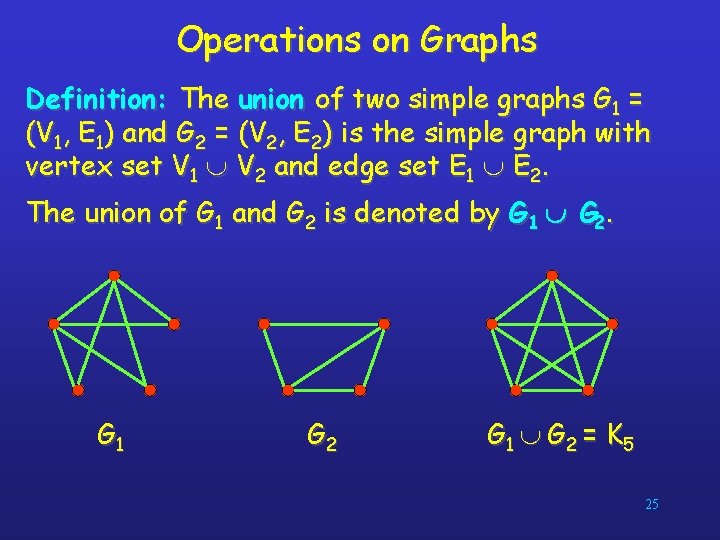
Operations on Graphs Definition: The union of two simple graphs G 1 = (V 1, E 1) and G 2 = (V 2, E 2) is the simple graph with vertex set V 1 V 2 and edge set E 1 E 2. The union of G 1 and G 2 is denoted by G 1 G 2. G 1 G 2 G 1 G 2 = K 5 25
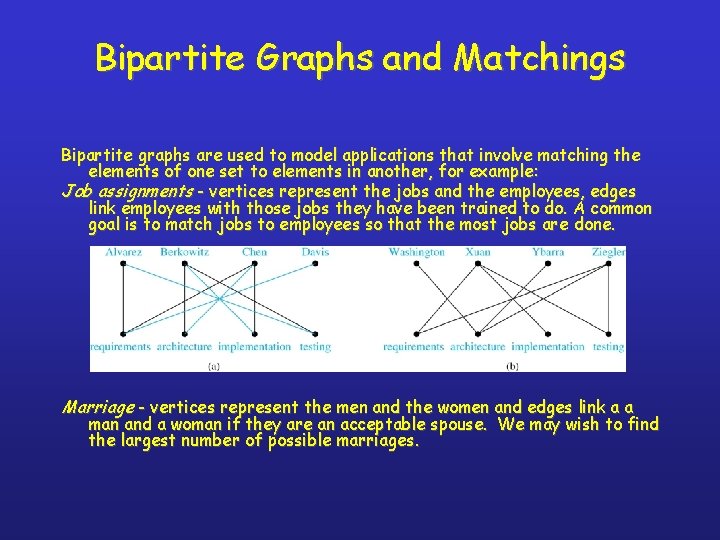
Bipartite Graphs and Matchings Bipartite graphs are used to model applications that involve matching the elements of one set to elements in another, for example: Job assignments - vertices represent the jobs and the employees, edges link employees with those jobs they have been trained to do. A common goal is to match jobs to employees so that the most jobs are done. Marriage - vertices represent the men and the women and edges link a a man and a woman if they are an acceptable spouse. We may wish to find the largest number of possible marriages.

Bipartite Graphs and Matchings A matching M in a simple graph G = (V , E) is a subset of the set E of edges of the graph such that no two edges are incident with the same vertex. A vertex that is the endpoint of an edge of a matching M is said to be matched in M; otherwise it is said to be unmatched. A maximum matching is a matching with the largest number of edges. A matching M in a bipartite graph G = (V , E) with bipartition (V 1, V 2) is a complete matching from V 1 to V 2 if every vertex in V 1 is the endpoint of an edge in the matching, or equivalently, if |M| = |V 1|. For example, to assign jobs to employees so that the largest number of jobs are assigned employees, we seek a maximum matching. To assign employees to all jobs we seek a complete matching from the set of jobs to the set of employees.

Bipartite Graphs and Matchings HALL’S MARRIAGE THEOREM (1935) The bipartite graph G = (V , E) with bipartition (V 1, V 2) has a complete matching from V 1 to V 2 if and only if |N(A)| ≥ |A| for all subsets A of V 1.
- Slides: 28