Graphs Chapter 19 Chapter Contents l Some Examples




















![Kruskal's Algorithm l Ordered edges: [1, 4], [6, 7], [3, 4], [1, 2], [4, Kruskal's Algorithm l Ordered edges: [1, 4], [6, 7], [3, 4], [1, 2], [4,](https://slidetodoc.com/presentation_image_h/a42330d1bde5a96477b19bf0d72b9a10/image-43.jpg)



- Slides: 51

Graphs Chapter 19

Chapter Contents l Some Examples and Terminology l l l l Road Maps Airline Routes Mazes Course Prerequisites Trees Traversals l l Breadth-First Traversal Dept-First Traversal Topological Order Paths l l Finding a Path Shortest Path in an Unweighted Graph Shortest Pat in a Weighted Graph Java Interfaces for the ADT Graph 2

Some Examples and Terminology l A graph is a collection of distinct vertices and distinct edges l l Edges can be directed or undirected When it has directed edges it is called a digraph Vertices or nodes are connected by edges A subgraph is a portion of a graph that itself is a graph 3

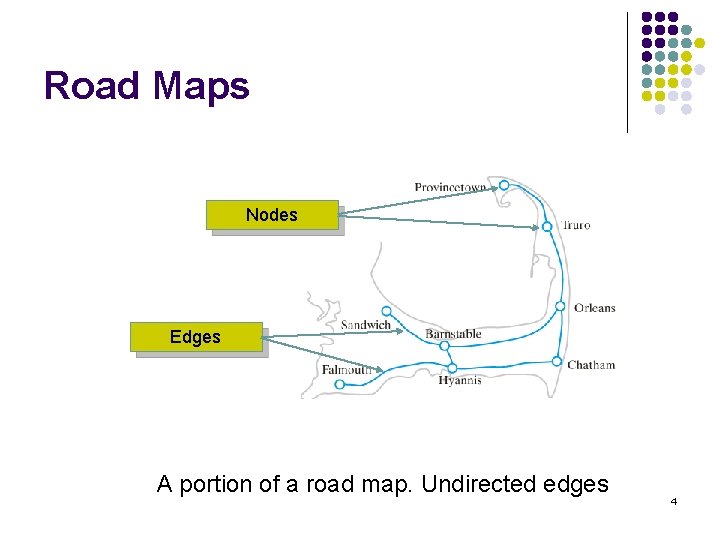
Road Maps Nodes Edges A portion of a road map. Undirected edges 4

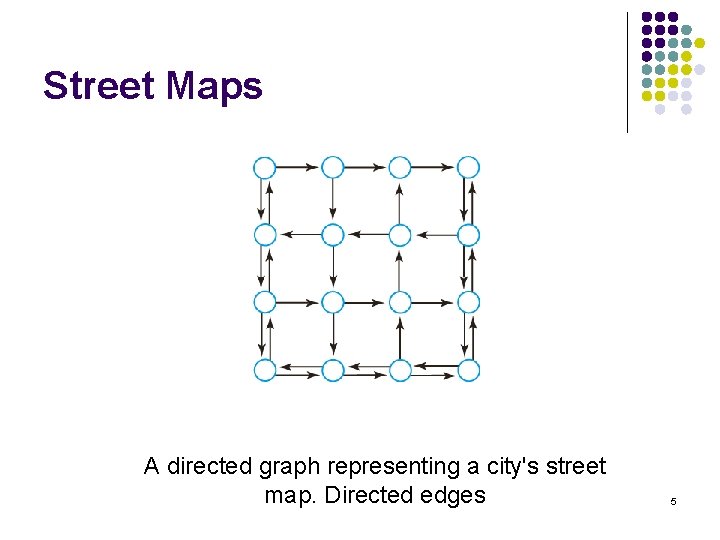
Street Maps A directed graph representing a city's street map. Directed edges 5

Path l l A sequence of edges that connect two vertices in a graph In a directed graph the direction of the edges must be considered l l A cycle is a path that begins and ends at same vertex l l Called a directed path Simple path does not pass through any vertex more than once A graph with no cycles is acyclic 6

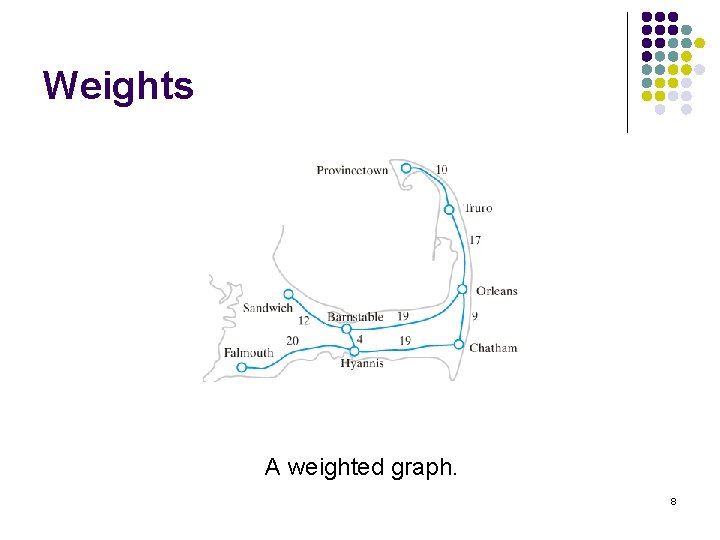
Weight l A weighted graph has values on its edges l l A path in a weighted graph also has weight or cost l l Weights or costs The sum of the edge weights Examples of weights l l l Miles between nodes on a map Driving time between nodes Taxi cost between node locations 7

Weights A weighted graph. 8

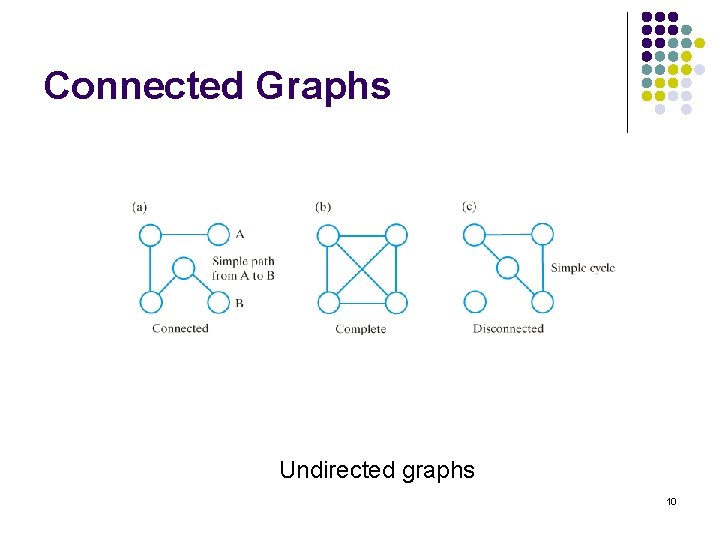
Connected Graphs l A connected graph l l A complete graph l l Has a path between every pair of distinct vertices Has an edge between every pair of distinct vertices A disconnected graph l Not connected 9

Connected Graphs Undirected graphs 10

Adjacent Vertices l l Two vertices are adjacent in an undirected graph if they are joined by an edge Sometimes adjacent vertices are called neighbors Vertex A is adjacent to B, but B is not adjacent to A. 11

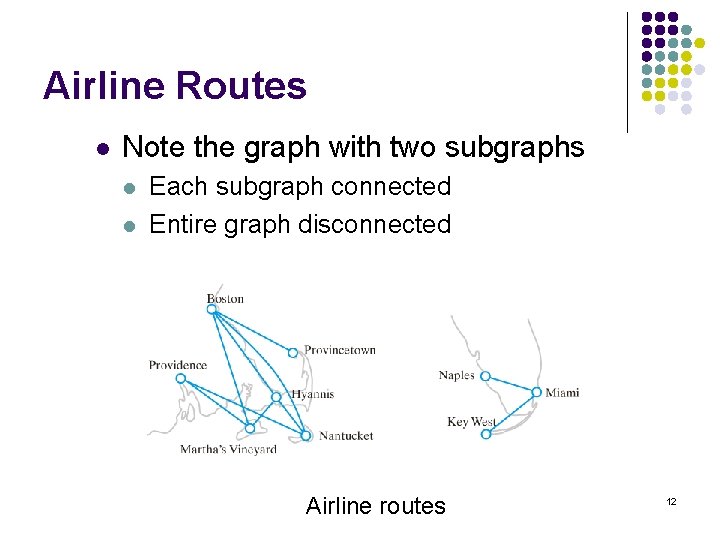
Airline Routes l Note the graph with two subgraphs l l Each subgraph connected Entire graph disconnected Airline routes 12

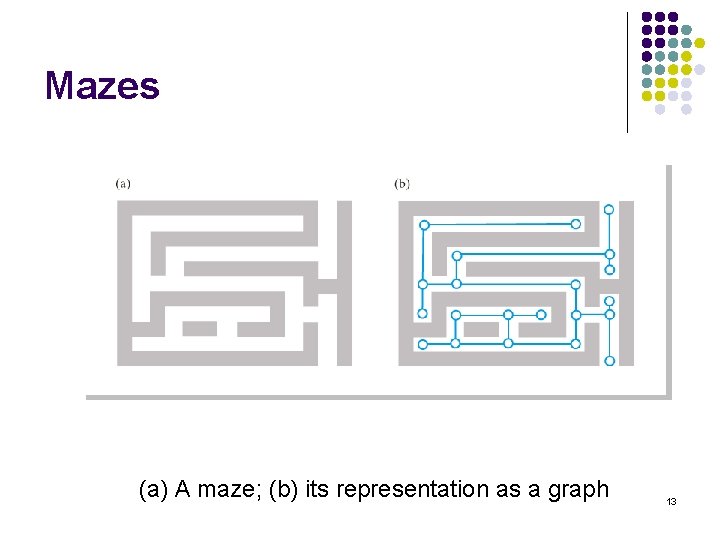
Mazes (a) A maze; (b) its representation as a graph 13

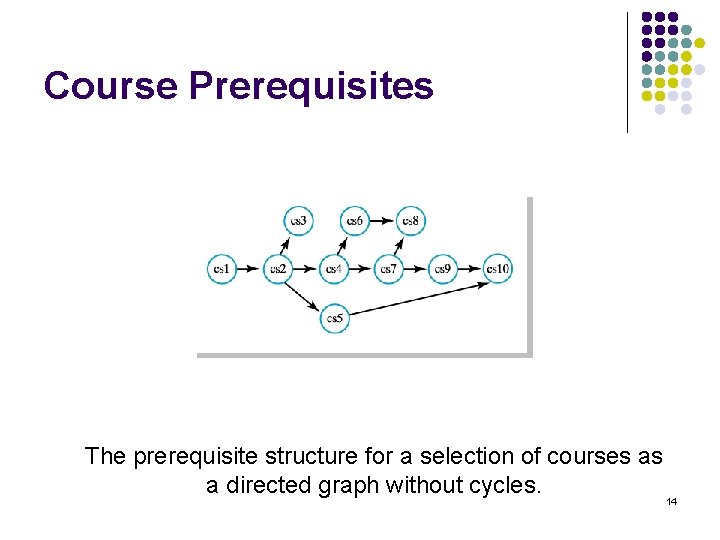
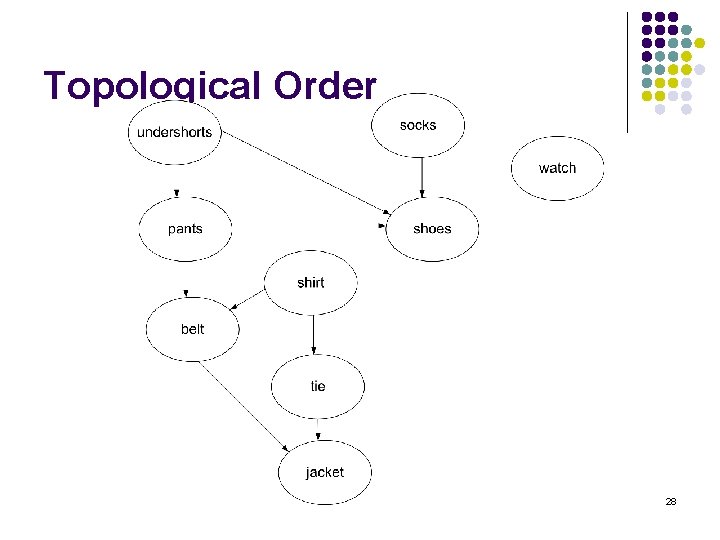
Course Prerequisites The prerequisite structure for a selection of courses as a directed graph without cycles. 14

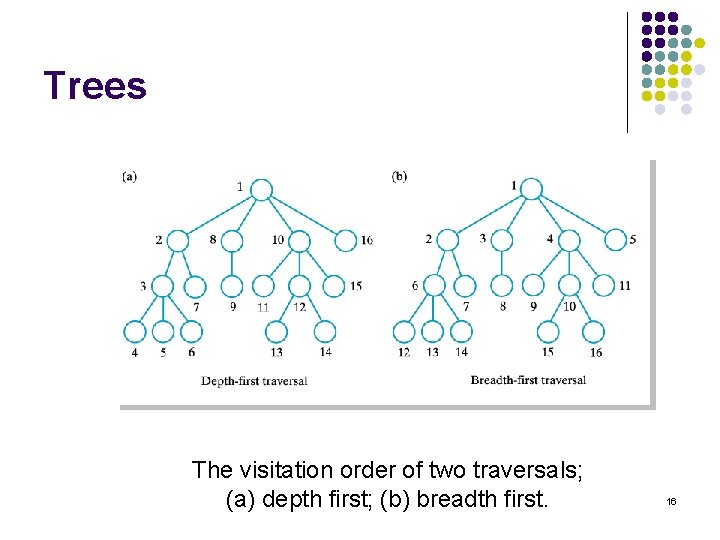
Trees l All trees are graphs l l l A tree is a connected graph without cycles Traversals l l l But not all graphs are trees Preorder, inorder, postorder traversals are examples of depth-first traversal Level-order traversal of a tree is an example of breadth-first traversal Visit a node l l For a tree: process the node's data For a graph: mark the node as visited 15

Trees The visitation order of two traversals; (a) depth first; (b) breadth first. 16

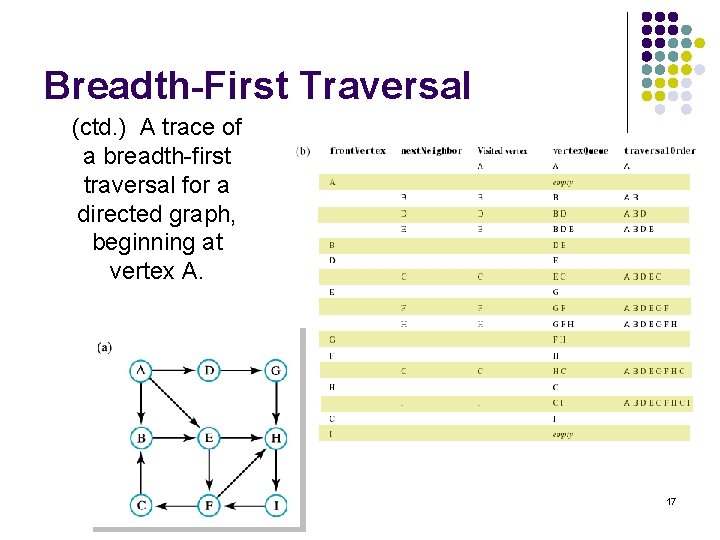
Breadth-First Traversal (ctd. ) A trace of a breadth-first traversal for a directed graph, beginning at vertex A. 17

Breadth-First Traversal l Algorithm for breadth-first traversal of nonempty graph beginning at a given vertex Algorithm get. Breadth. First. Traversal(origin. Vertex) vertex. Queue = a new queue to hold neighbors traversal. Order = a new queue for the resulting traversal order Mark origin. Vertex as visited A breadth-first traversal visits traversal. Order. enqueue(origin. Vertex) a vertex and then each of the vertex. Queue. enqueue(origin. Vertex) vertex's neighbors before while (!vertex. Queue. is. Empty()) advancing { front. Vertex = vertex. Queue. dequeue() while (front. Vertex has an unvisited neighbor) { next. Neighbor = next unvisited neighbor of front. Vertex Mark next. Neighbor as visited traversal. Order. enqueue(next. Neighbor) vertex. Queue. enqueue(next. Neighbor) } } 18 return traversal. Order

Depth-First Traversal l Visits a vertex, then l l l A neighbor of the vertex, A neighbor of the neighbor, Etc. Visit them, and push them into stack Advance as much as possible from the original vertex When no unvisited neighbor exists, back up by one level by popping up current vertex l Considers the next neighbor branch 19

Depth-First Traversal A trace of a depth-first traversal beginning at vertex A of the directed graph 20

Depth-First Traversal Algorithm get. Depth. First. Traversal(origin. Vertex) vertex. Stack = a new stack to hold vertices as they are visited traversal. Order = a new queue for the resulting traversal order Mark origin. Vertex as visited traversal. Order. enqueue(origin. Vertex) vertex. Stack. push(origin. Vertex) while (!vertex. Stack. is. Empty()) { top. Vertex = vertex. Stack. peek() if (top. Vertex has an unvisited neighbor) { next. Neighbor = next unvisited neighbor of top. Vertex Mark next. Neighbor as visited traversal. Order. enqueue(next. Neighbor) vertex. Stack. push(next. Neighbor) } else // all neighbors are visited vertex. Stack. pop() 21

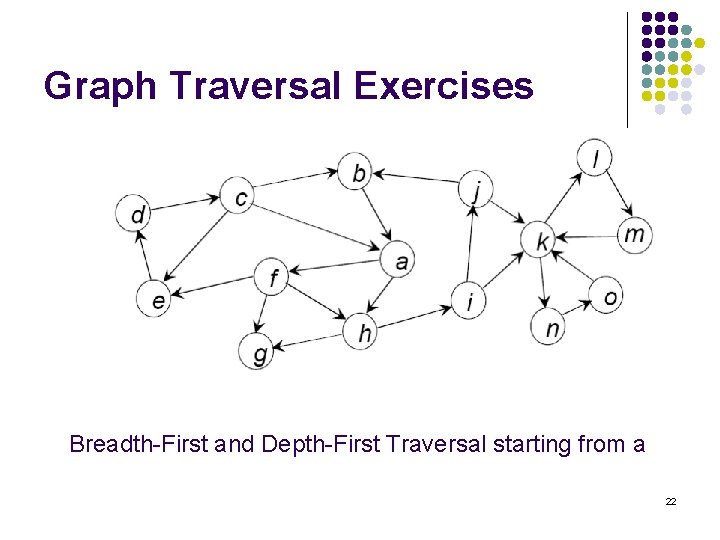
Graph Traversal Exercises Breadth-First and Depth-First Traversal starting from a 22

Some of the possible Answers l Breadth-first l l a f h e g i d j k c l n b m o Depth-first l a f e d c b g h i j k l m n o 23

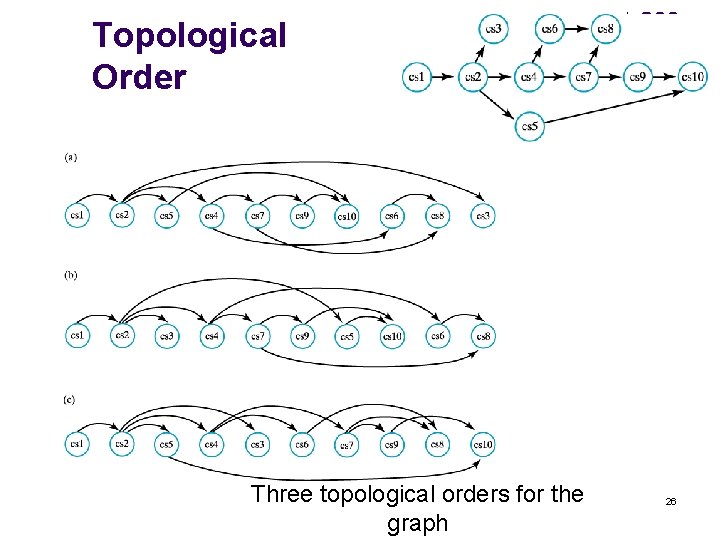
Topological Order l l l Given a directed graph without cycles (DAG) An ordering of vertices in a directed acyclic graph. In a topological order l l Vertex a precedes vertex b whenever A directed edge exists from a to b 24

Topological Order l l First find any vertex with no incoming edges. Print this vertex, and remove it, along with its edges from the graph. Then we apply the same strategy to the rest of graph. Indegree of node: Incoming number of edges 25

Topological Order Three topological orders for the graph 26

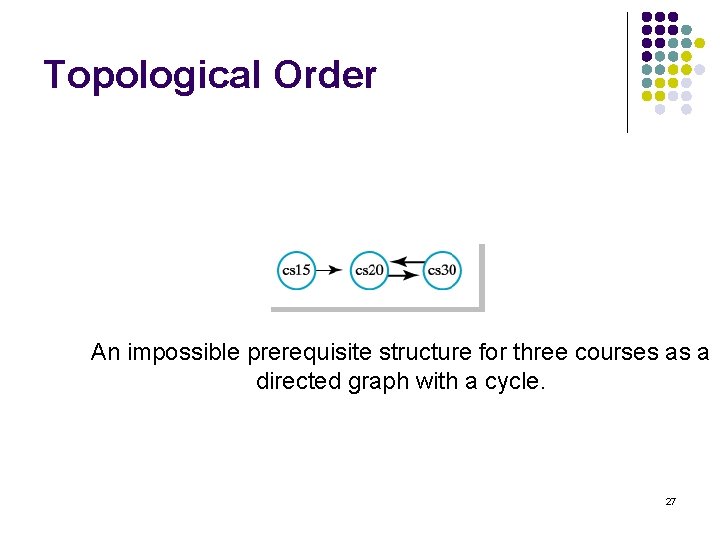
Topological Order An impossible prerequisite structure for three courses as a directed graph with a cycle. 27

Topological Order 28

Topological Order 29

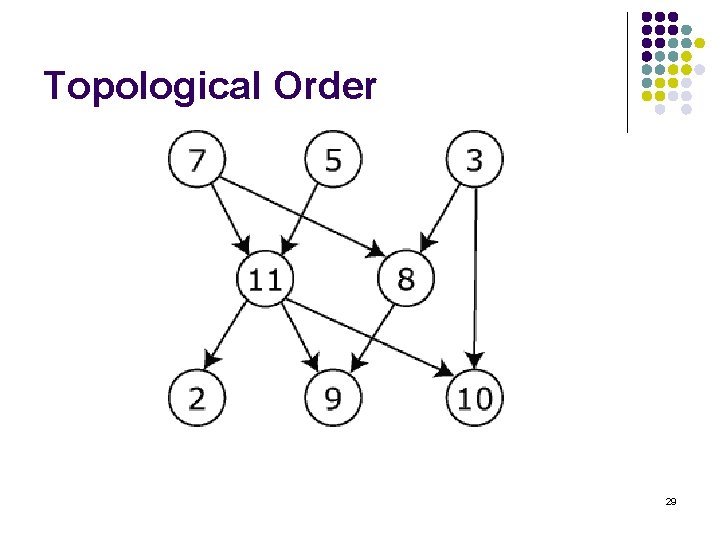
Topological Order l l The graph shown has many valid topological sorts, including: 7, 5, 3, 11, 8, 2, 9, 10 7, 5, 11, 2, 3, 10, 8, 9 3, 7, 8, 5, 11, 10, 9, 2 30

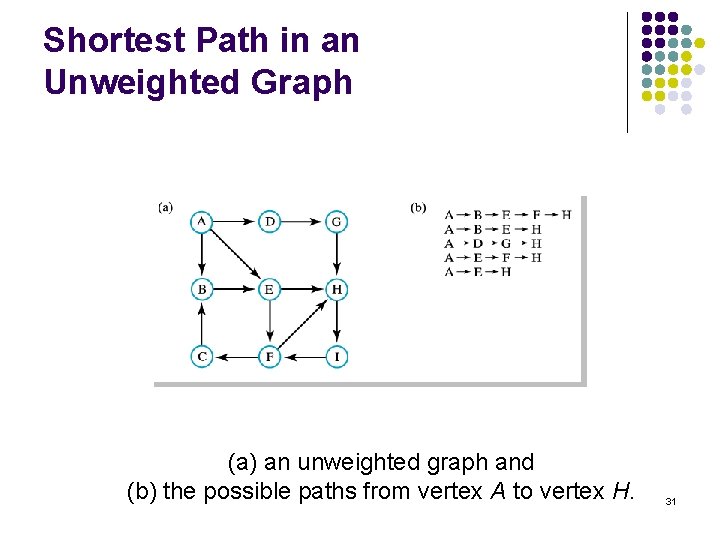
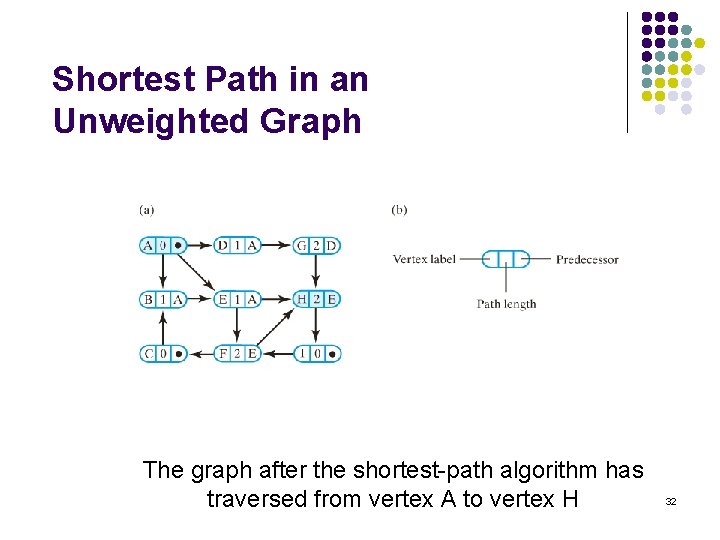
Shortest Path in an Unweighted Graph (a) an unweighted graph and (b) the possible paths from vertex A to vertex H. 31

Shortest Path in an Unweighted Graph The graph after the shortest-path algorithm has traversed from vertex A to vertex H 32

Shortest Path in an Unweighted Graph Finding the shortest path from vertex A to vertex H in the 33 unweighted graph

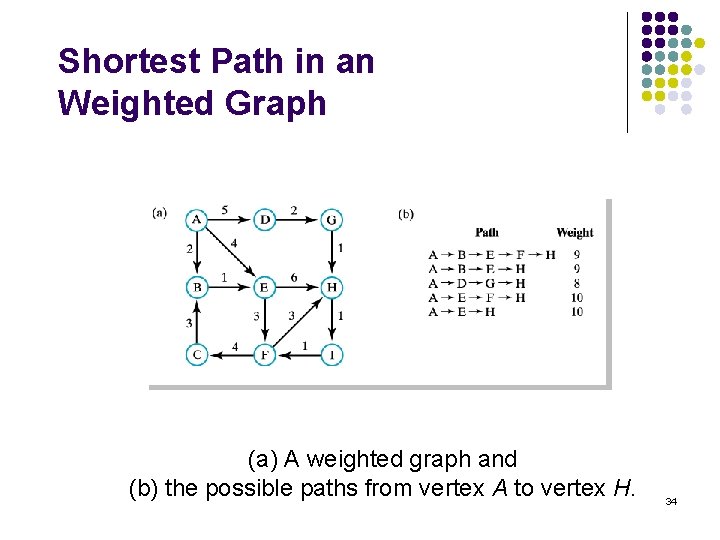
Shortest Path in an Weighted Graph (a) A weighted graph and (b) the possible paths from vertex A to vertex H. 34

Shortest Path in an Weighted Graph l Shortest path between two given vertices l l l Smallest edge-weight sum Algorithm based on breadth-first traversal (Dijkstra algorithm) Several paths in a weighted graph might have same minimum edge-weight sum l Algorithm given by text finds only one of these paths 35

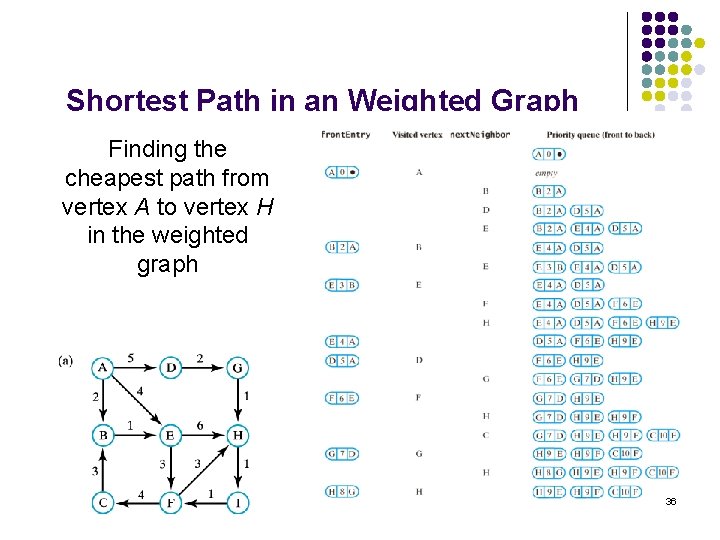
Shortest Path in an Weighted Graph Finding the cheapest path from vertex A to vertex H in the weighted graph 36

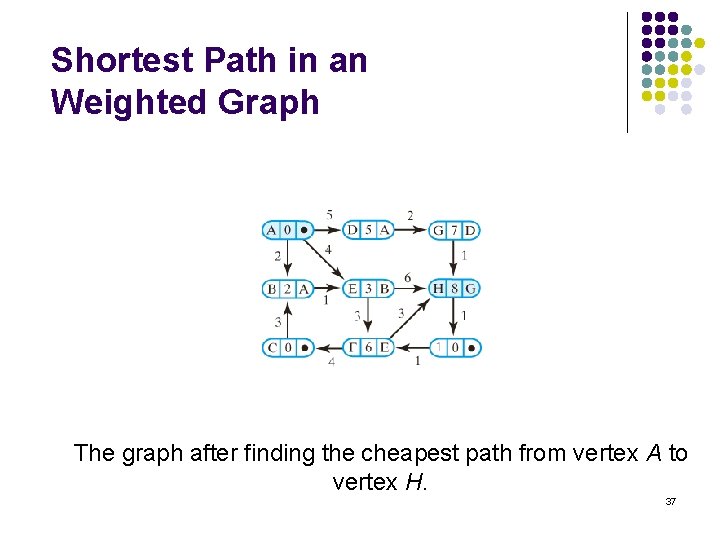
Shortest Path in an Weighted Graph The graph after finding the cheapest path from vertex A to vertex H. 37

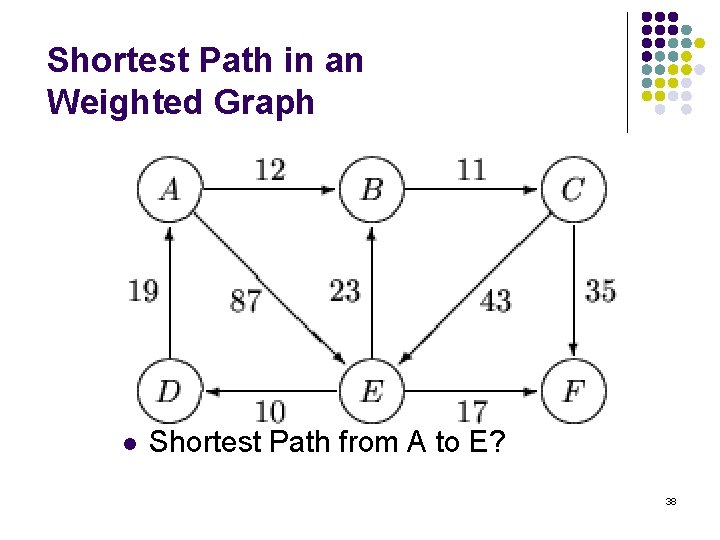
Shortest Path in an Weighted Graph l Shortest Path from A to E? 38

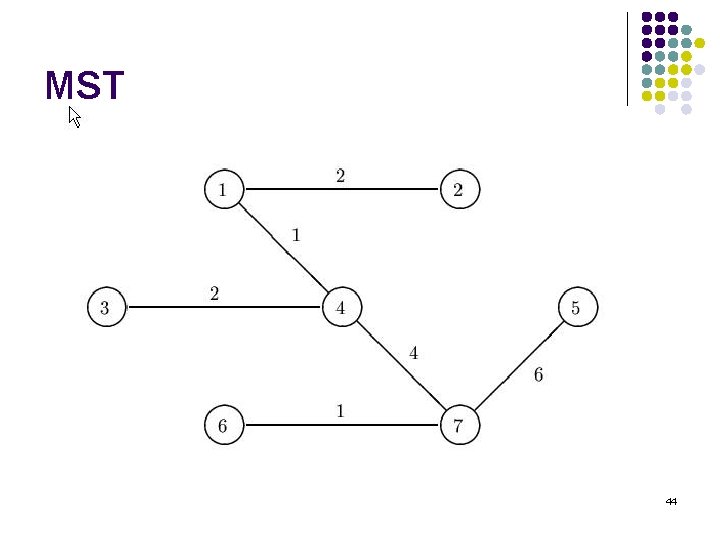
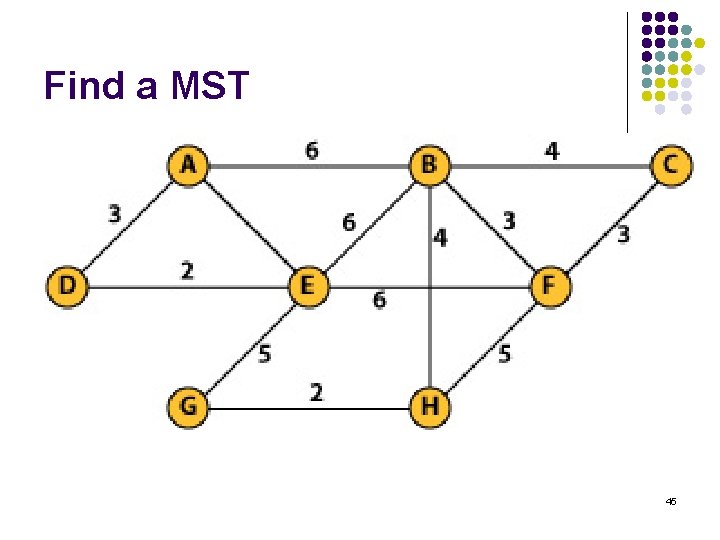
Minimum Spanning Tree l l The minimum spanning tree (MST) of a graph defines the cheapest subset of edges that keeps the graph in one connected component. Telephone companies are particularly interested in minimum spanning trees, because the minimum spanning tree of a set of sites defines the wiring scheme that connects the sites using as little wire as possible. 39

Greedy Algorithm l l Greedy algorithms work in phases. In each phase, a decision is made that appears to be good, without regard for future consequences. A greedy algorithm makes the locally optimum choice at each phase with the hope of finding the global optimum. 40

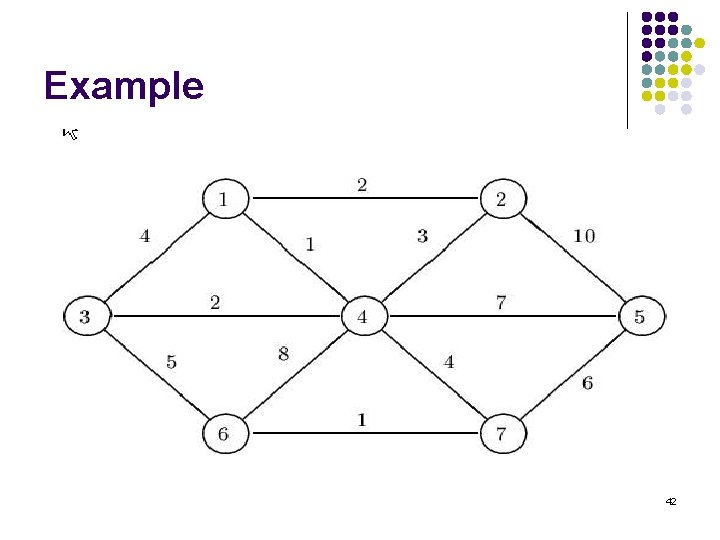
Kruskal's Algorithm l l l Let G be a connected graph with n vertices Initialize n components, each one containing one vertex of G. Now sort the edges in increasing order by weight and set T = the empty set. Now examine each edge in turn. If an edge joins two components, add it to T and merge the two components into one. If not, discard the edge. Stop when only one component remains. 41

Example 42
![Kruskals Algorithm l Ordered edges 1 4 6 7 3 4 1 2 4 Kruskal's Algorithm l Ordered edges: [1, 4], [6, 7], [3, 4], [1, 2], [4,](https://slidetodoc.com/presentation_image_h/a42330d1bde5a96477b19bf0d72b9a10/image-43.jpg)
Kruskal's Algorithm l Ordered edges: [1, 4], [6, 7], [3, 4], [1, 2], [4, 2], [3, 1], [4, 7], [3, 6], [7, 5], [4, 5], [6, 4], [2, 5] l Components l T (edges) 1, 2, 3, 4, 5, 6, 7 empty [1, 4], 2, 3, 5, 6, 7 [1, 4], 2, 3, 5, [6, 7] [1, 4], [6, 7] [1, 4, 3], 2, 5, [6, 7] [1, 4], [6, 7], [3, 4] [1, 4, 3, 2], 5, [6, 7] [1, 4], [6, 7], [3, 4], [1, 2] [1, 4, 3, 2, 6, 7], 5 [1, 4], [6, 7], [3, 4], [1, 2], [4, 7] [1, 4, 3, 2, 6, 7, 5] [1, 4], [6, 7], [3, 4], [1, 2], [4, 7], [7, 5] 43

MST 44

Find a MST 45

Java Interfaces for the ADT Graph l Methods in the Basic. Graph. Interface l l l l add. Vertex add. Edge has. Edge is. Empty get. Number. Of. Vertices get. Number. Of. Edges clear 46

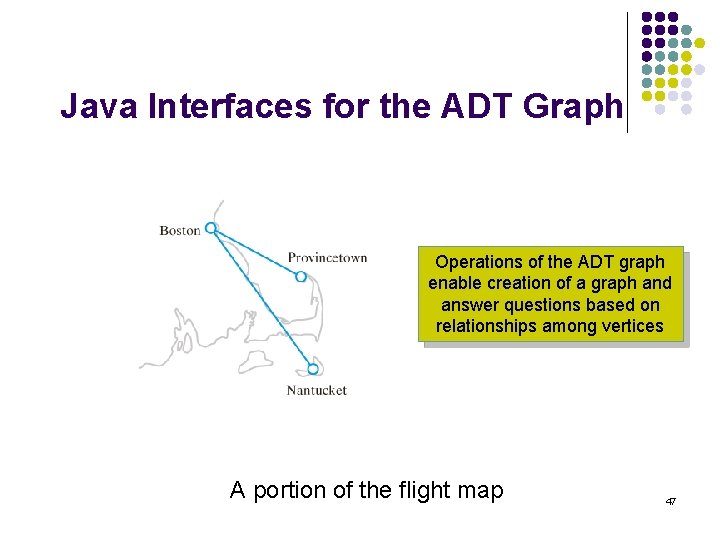
Java Interfaces for the ADT Graph Operations of the ADT graph enable creation of a graph and answer questions based on relationships among vertices A portion of the flight map 47

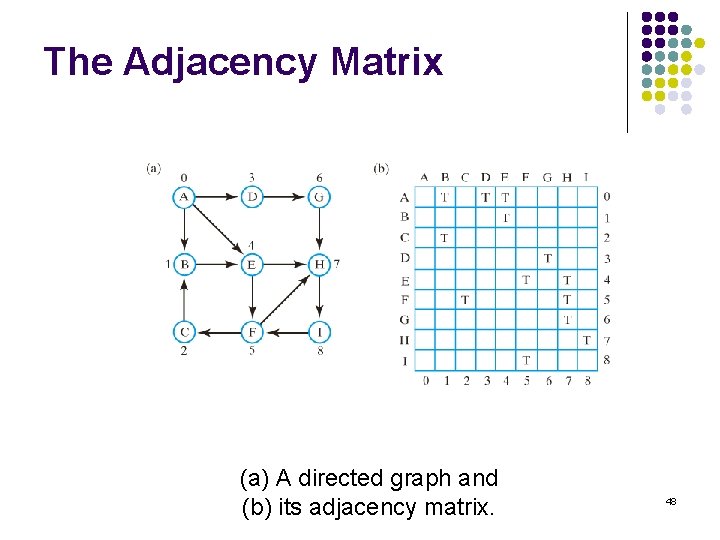
The Adjacency Matrix (a) A directed graph and (b) its adjacency matrix. 48

The Adjacency Matrix l Adjacency matrix uses fixed amount of space l l l Depends on number of vertices Does not depend on number of edges Typically the matrix will be sparse Presence of an edge between two vertices can be known immediately All neighbors of a vertex found by scanning entire row for that vertex 49

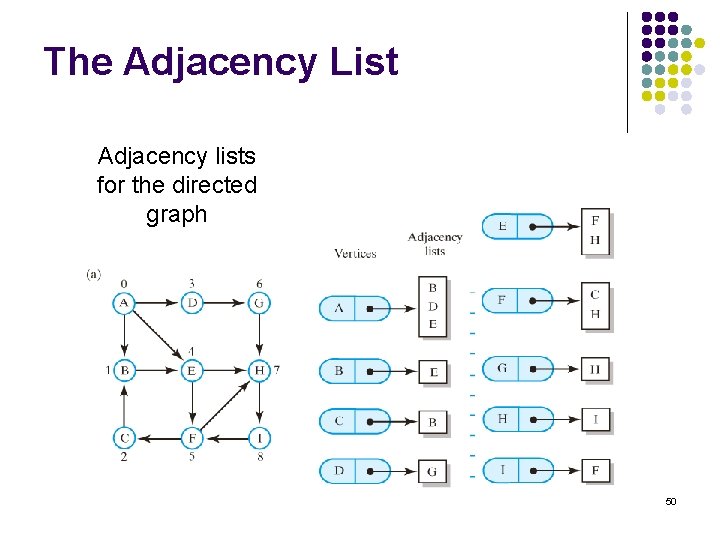
The Adjacency List Adjacency lists for the directed graph 50

The Adjacency List l l Represents only edges that originate from the vertex Space not reserved for edges that do not exist l l Uses less memory than corresponding adjacency matrix Thus more often used than adjacency matrix 51