Graphs Chapter 12 B Ramamurthy 1 Introduction A

Graphs Chapter 12 B. Ramamurthy 1

Introduction A structure that represents connectivity information. A tree is kind of graph. Applications include maps in geographic information system, transportation, electrical circuits, and computer network and our project 3’s Scotland Yard map. B. Ramamurthy 2

Graph ADT A graph G is a pair {V, E} where V is a set of vertices, and E is a collection of pairs of vertices from V, called the edges. Vertices == nodes, edges == arcs Edges can be directed or undirected. Directed graph: all edges are directed (digraph) Undirected graph: all edges are undirected Mixed graph: There also mixed graphs: City map with one-way routes is an example for mixed graph. B. Ramamurthy 3

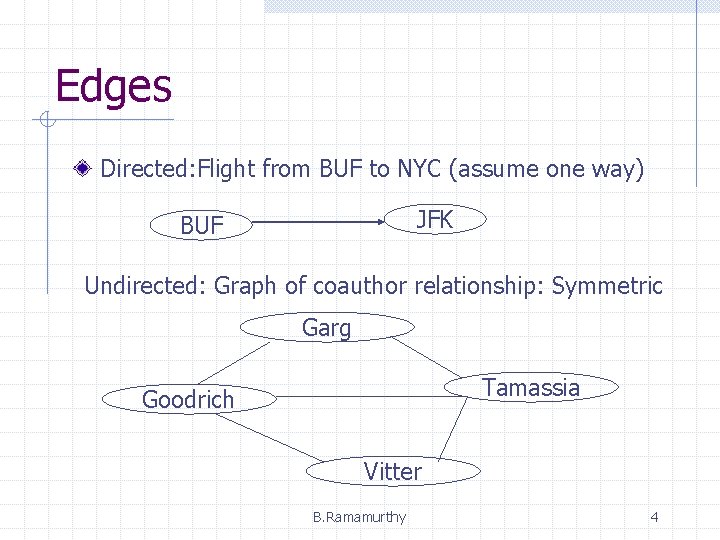
Edges Directed: Flight from BUF to NYC (assume one way) JFK BUF Undirected: Graph of coauthor relationship: Symmetric Garg Tamassia Goodrich Vitter B. Ramamurthy 4

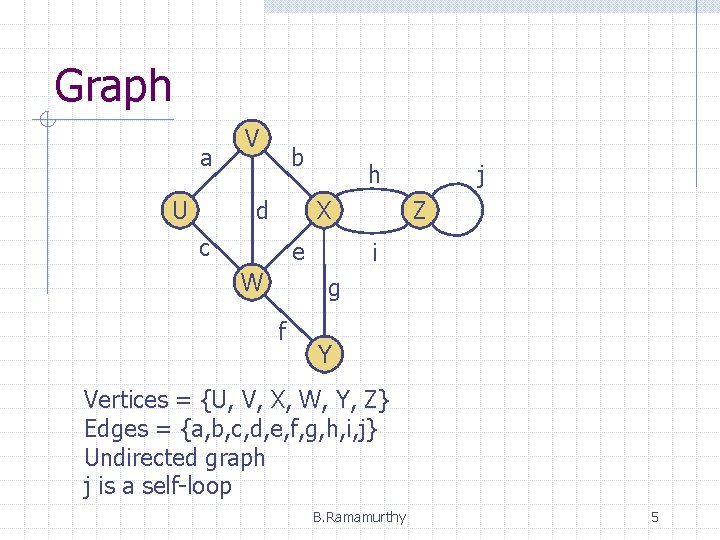
Graph a V b d U h X c e W j Z i g f Y Vertices = {U, V, X, W, Y, Z} Edges = {a, b, c, d, e, f, g, h, i, j} Undirected graph j is a self-loop B. Ramamurthy 5

Path is a sequence of alternating vertices and edges that starts at a vertex and ends at a vertex. Example: {W, c, U, a, V} A simple path is a path where all its vertices and edges are distinct Cycle is a path where the start and end vertices are the same. B. Ramamurthy 6

Graph Properties Adjacency: Two vertices are said to be adjacent if they are end points of the same edge. Incoming edge: of a vertex is an edge whose destination is that vertex. Outgoing edge: of a vertex is an edge whose origin is that vertex. The in-degree and out-degree of a vertex v are the number of incoming and outgoing edges respectively. Degree of a vertex is in-degree + out-degree B. Ramamurthy 7

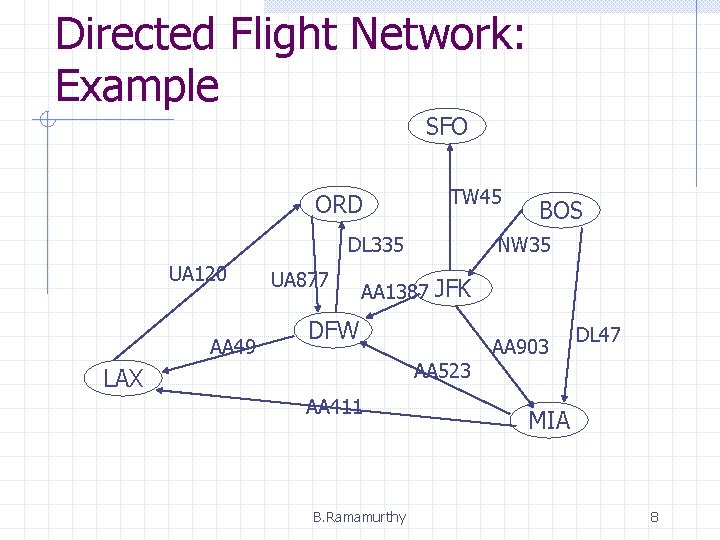
Directed Flight Network: Example SFO ORD TW 45 DL 335 UA 120 AA 49 UA 877 BOS NW 35 AA 1387 JFK DFW AA 523 LAX AA 411 B. Ramamurthy AA 903 DL 47 MIA 8

Graph ADT (Tomassia and Goodrich’s text) Vertices and edges n n Update methods are positions store elements n n Accessor methods n n n n n a. Vertex() incident. Edges(v) end. Vertices(e) is. Directed(e) origin(e) destination(e) opposite(v, e) are. Adjacent(v, w) n n insert. Vertex(o) insert. Edge(v, w, o) insert. Directed. Edge(v, w, o) remove. Vertex(v) remove. Edge(e) Generic methods n n B. Ramamurthy num. Vertices() num. Edges() vertices() edges() 9

Implementation of Graph ADT Matrix (a two dimensional array): adjacency matrix Vertices are used for row and column index Entry in a cell indicates an edge between the vertex at row index and vertex at column index. B. Ramamurthy 10

Airline Graph Matrix (p. 555) B. Ramamurthy 11

Adjacency List When a matrix is sparsely filled it is called a sparse matrix. Sparse matrix can be simplified into lists, row-lists, column-list, or cell type lists Location (from) Location(to) Transportation(bus, taxi, train) Scotland Yard Board 12