Graphs C Data Structure Runtimes Data Structure Insert

Graphs

C++ Data Structure Runtimes Data Structure Insert Find Delete vector O(n) O(1) amortized O(n) O(1) if index is known O(n) sorted vector O(n) O(log(n)) O(n) linked list (list, stack, queue) O(1) *Given an Iterator O(n) O(1) *Given an Iterator balanced binary tree (map, set) O(log(n)) hash table (unordered_set, unordered_map) O(1) Heap (priority_queue) O(log(n)) N/A O(1) to find min O(log(n))

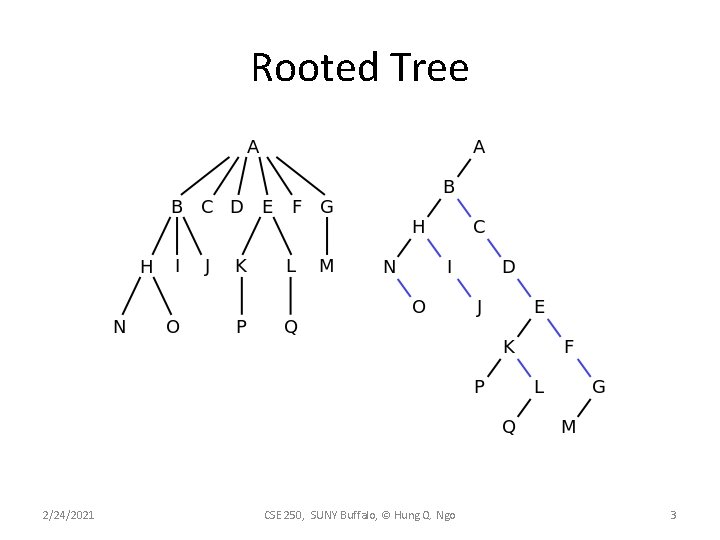
Rooted Tree 2/24/2021 CSE 250, SUNY Buffalo, © Hung Q. Ngo 3

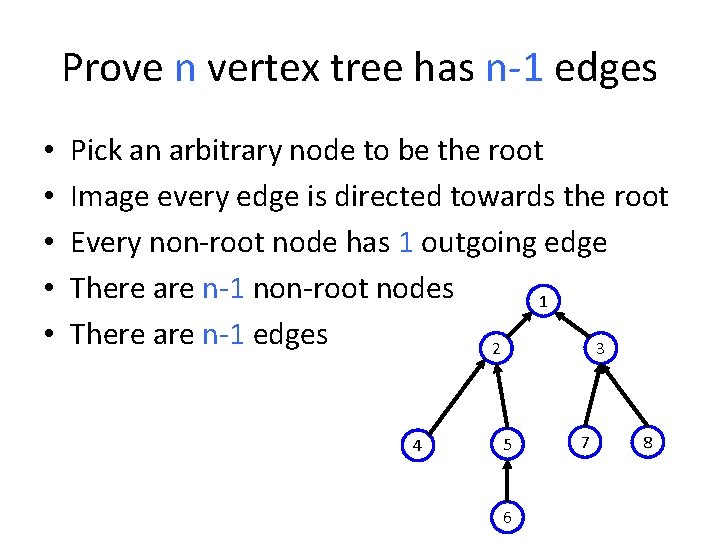
Prove a tree with n vertices has n -1 edges

Prove n vertex tree has n-1 edges • • • Pick an arbitrary node to be the root Image every edge is directed towards the root Every non-root node has 1 outgoing edge There are n-1 non-root nodes 1 There are n-1 edges 2 3 4 5 6 7 8

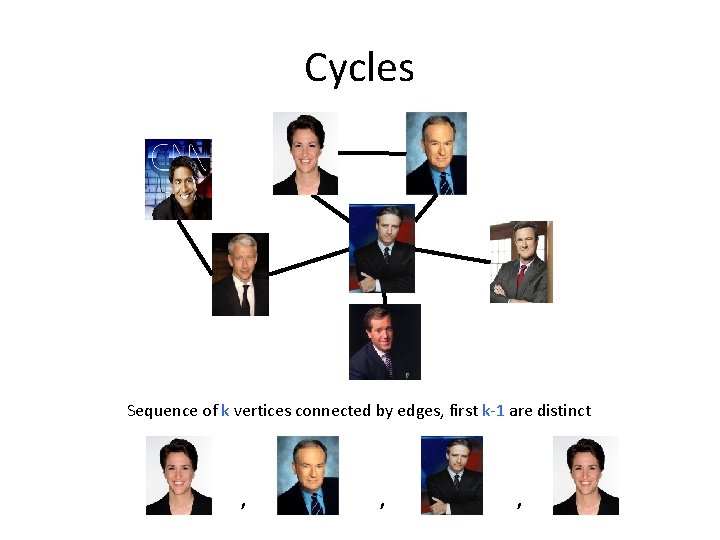
Trees -> Graphs • We’ve only seen rooted trees – Trees don’t need to be rooted • All Trees are graphs • Not all graphs are trees • What if we add another edge to a tree?

Cycles Sequence of k vertices connected by edges, first k-1 are distinct , , ,

Graphs • Consists of – Nodes – Edges • Node – Contains information – Data depends on application • Edge – Connects 2 nodes – Definition of connected depends on application

Graphs are omnipresent Airline Route maps

What does this graph represent? Internet

And this one? Math articles on Wikipedia

And this one?

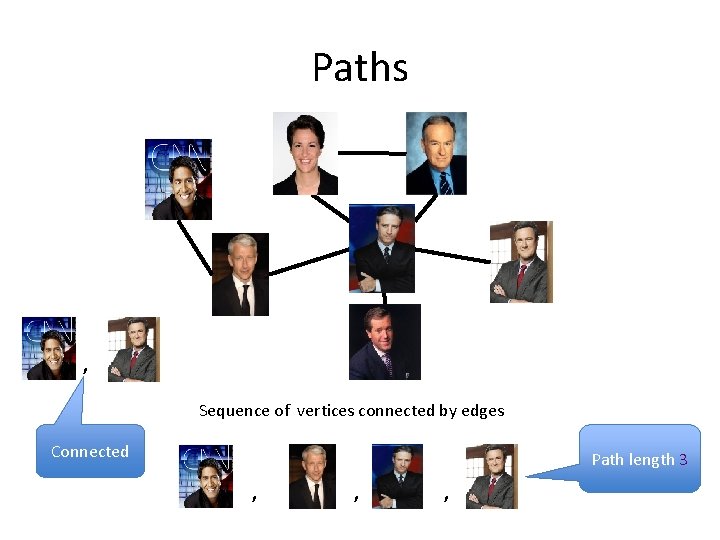
Paths , Sequence of vertices connected by edges Connected Path length 3 , , ,

Connectivity u and w are connected iff there is a path between them A graph is connected iff all pairs of vertices are connected

Questions About Graphs • Are two nodes in a graph connected? • What is the shortest path to travel between two nodes? • Give the set of nodes connected to a node by at most 3 edges?

What about large graphs? s t Are s and t connected?

Discussion: How to Store a Graph? What Data Structures will we use?

First Some Definitions • n – The number of nodes in a graph • m – The number of edges in a graph • nv – The number of nodes connected to node v by a single edge (neighbors of v)

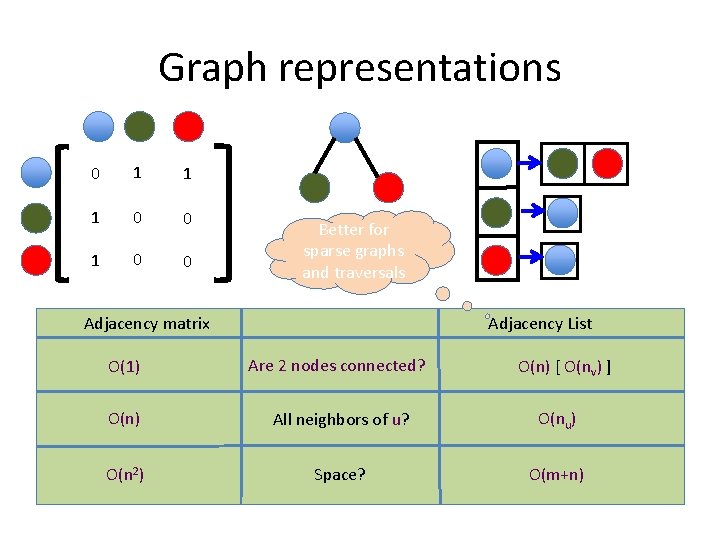
Graph representations 0 1 1 1 0 0 Better for sparse graphs and traversals Adjacency matrix Adjacency List O(1) Are 2 nodes connected? O(n) All neighbors of u? O(nu) O(n 2) Space? O(m+n) O(n) [ O(nv) ]

Graph Representations in C++ • No graph in STL • Combine STL data structures to represent a graph – Best representation depends on the application How do we represent a graph in C++?

Nodes • Graph stores – A collection of nodes – Tracks all edges • Query if nodes are connected

Adjacency List in C++

Adjacency List in C++

Playing it Safe • CSE 116 review • Protection from misuse of the function • Helps to find bugs

Adjacency List in C++ • Space – nodes. size() = number of nodes, n – adjacency list has 1 entry for every edge, m – Total space is n+m – Great for sparse graphs • Small m (<< n 2)

Adjacency List in C++ • Runtime of get. All. Neighbors – O(log(n)) – O(mu) to iterate list (number of neighbors of node) • Could we return the list in O(1) time? – unordered_map – hash table

Adjacency Matrix

Adjacency Matrix

Adjacency Matrix

Adjacency Matrix • Space – nodes. size() = number of nodes, n – adjacency matrix has 1 entry for every pair of nodes, O(n 2) – Total space is O(n 2)

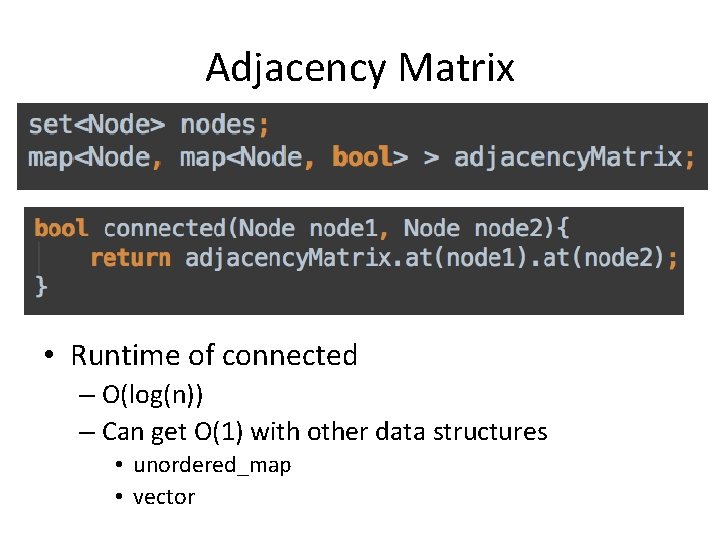
Adjacency Matrix • Runtime of connected – O(log(n)) – Can get O(1) with other data structures • unordered_map • vector

Adjacency Matrix - Alternate • If nodes have consecutive ID’s starting at 0 • Use ID’s to access vector in O(1) time • Not robust – Must maintain ID’s – Deleting a node means a missing row and column

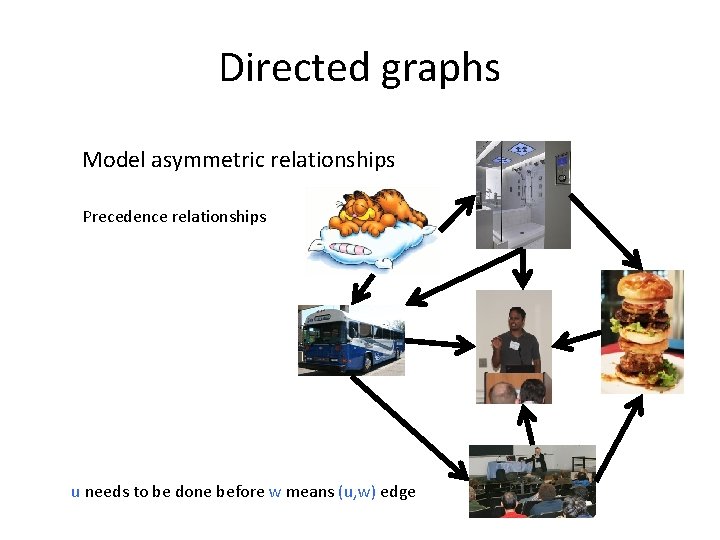
Directed graphs Model asymmetric relationships Precedence relationships u needs to be done before w means (u, w) edge