Graphs and Matrices Four Representations of a Graph

Graphs and Matrices

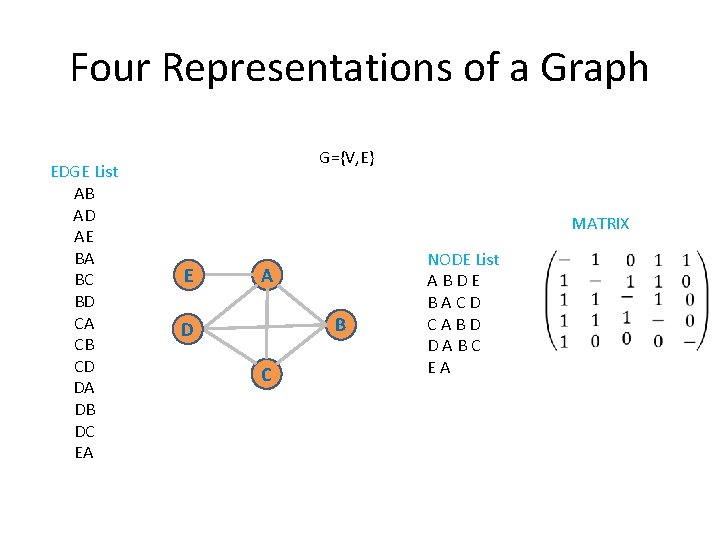
Four Representations of a Graph EDGE List AB AD AE BA BC BD CA CB CD DA DB DC EA G={V, E} MATRIX E A B D C NODE List ABDE BACD CABD DABC EA

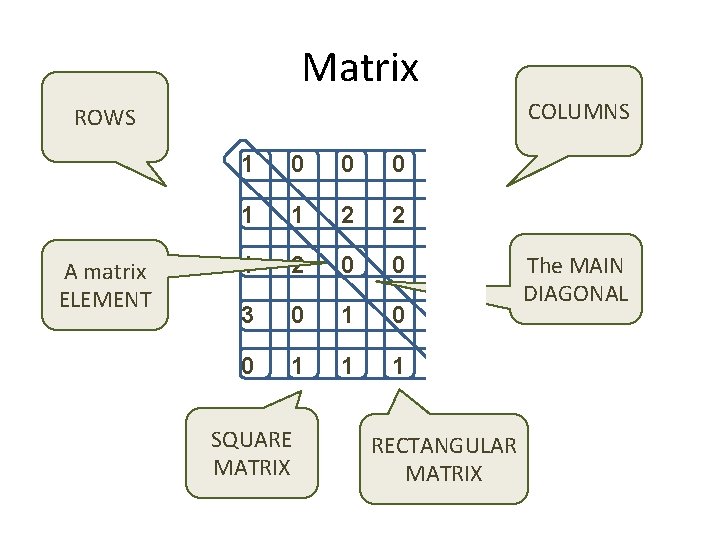
Matrix COLUMNS ROWS A matrix ELEMENT 1 0 0 0 1 1 1 2 2 0 1 2 0 0 0 3 0 1 0 0 0 1 1 SQUARE MATRIX RECTANGULAR MATRIX The MAIN DIAGONAL

Nomenclature: nrows by mcols 1 0 0 0 1 1 2 2 1 2 0 3 0 0 1 5 x 2 matrix 2 x 4 matrix 3 x 3 matrix 1 3 0 3 x 1 matrix

Matrix •

Sometimes we say “Vector” • Each row (or column) in a matrix can be thought of as an ordered set of numbers describing an object. • For a graph matrix, a row or a column is a “vector” of a vertex’s connections • The fourth vertex is connected to the first, second, and third, but not the fifth

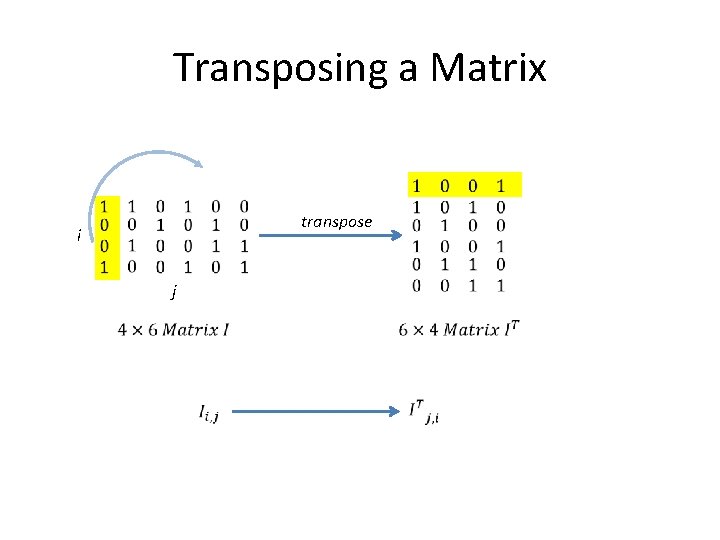
Transpose • The transpose of a matrix is a swapping of its rows and columns

Transposing a Matrix transpose i j

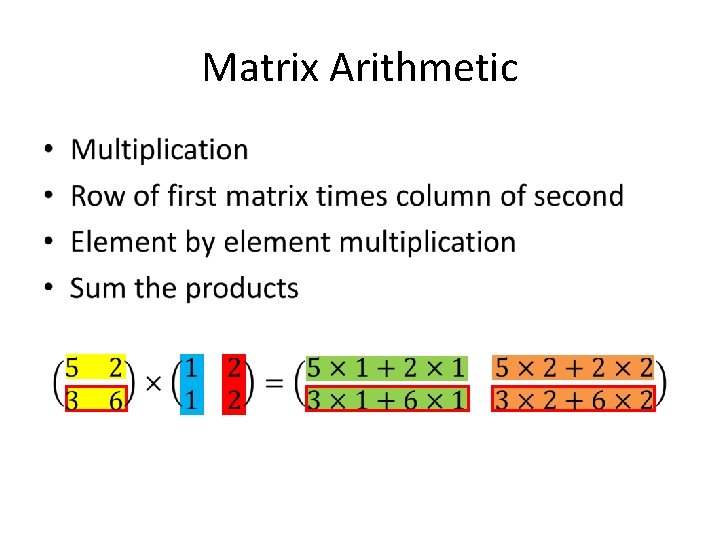
Matrix Arithmetic •

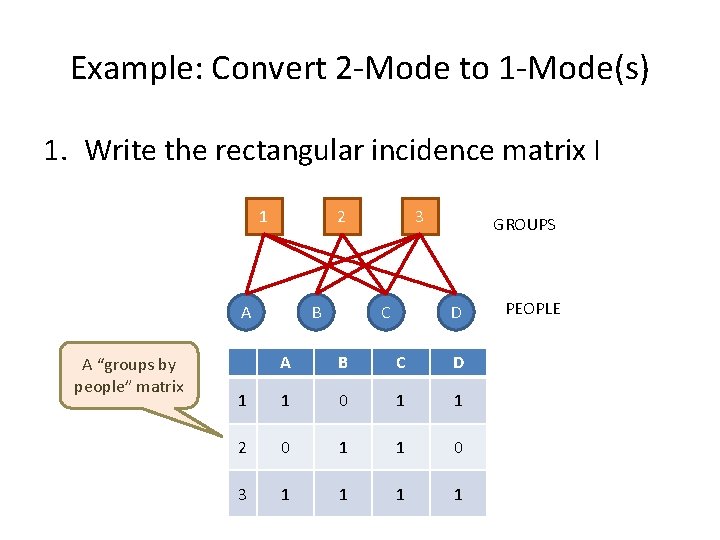
Example: Convert 2 -Mode to 1 -Mode(s) 1. Write the rectangular incidence matrix I 1 2 A A “groups by people” matrix B 3 C GROUPS D A B C D 1 1 0 1 1 2 0 1 1 0 3 1 1 PEOPLE

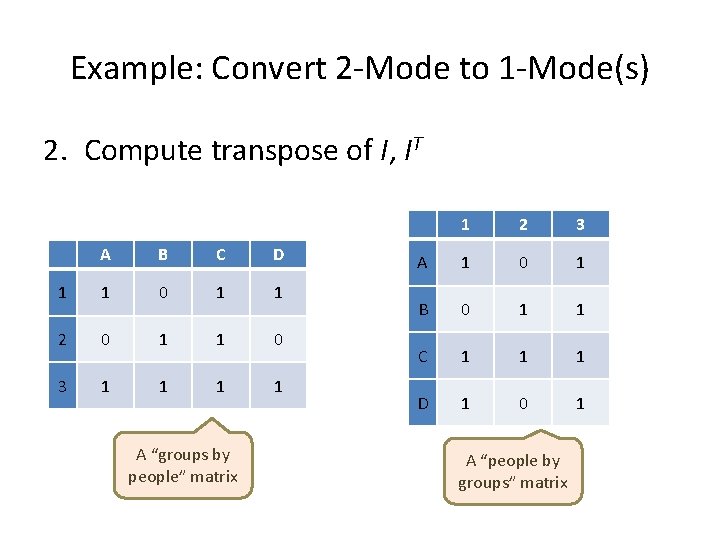
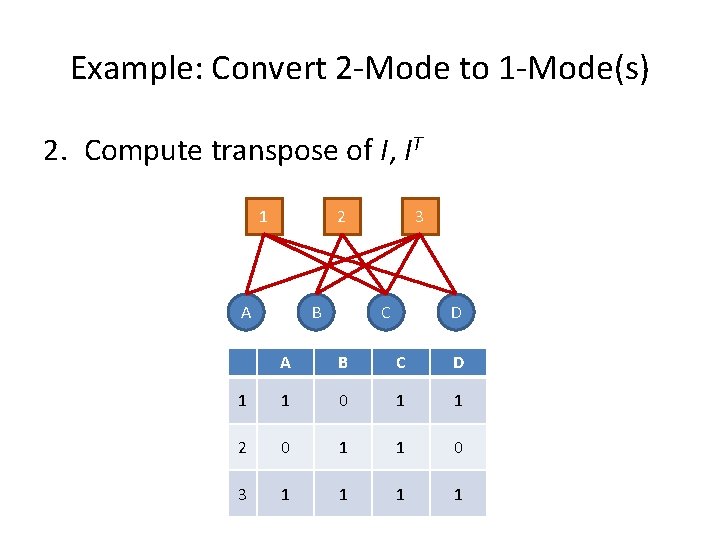
Example: Convert 2 -Mode to 1 -Mode(s) 2. Compute transpose of I, IT A B C D 1 1 0 1 1 2 0 1 1 0 3 1 1 A “groups by people” matrix 1 2 3 A 1 0 1 B 0 1 1 C 1 1 1 D 1 0 1 A “people by groups” matrix

When we multiply matrices… • Columns of first factor = rows of second factor • (People x Groups) X (Groups x People) = (People x People) • (Groups x People) X (People x Groups) = (Groups x Groups) I 1011 0110 x 1111 IT 101 011 101 AGx. G = 313 122 324 IT 101 011 101 I 1011 x 0110 = 1111 APx. P 2122 1221 2232 2122

Degree • 1 0 0 0 1 1 1 0 0 1 1 -

Mean(average) Degree •

Degree and Edges •

Adjacency Matrix •

Matrix Arithmetic • See also: http: //www. jtaylor 1142001. net/calcjat/Contents/CMatrix. htm#Matrix. Mult

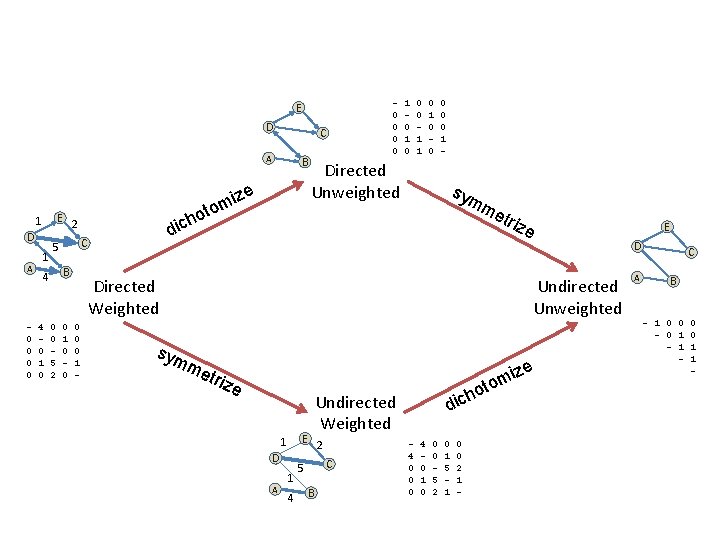
0 0 E D C A B e E 1 D A 0 0 1 4 0 1 0 C B 0 0 5 2 0 1 0 0 1 1 0 0 0 1 - Directed Unweighted sym me h dic 2 5 4 iz m o ot 1 0 triz e D Undirected Unweighted Directed Weighted 0 0 0 1 - E sym me triz e e E 1 D A 1 4 B dic Undirected Weighted 2 C 5 h iz m o ot 4 0 0 0 4 0 1 0 0 0 5 2 0 1 5 1 0 0 2 1 - A C B - 1 0 0 - 0 1 - 0 0 1 1 -

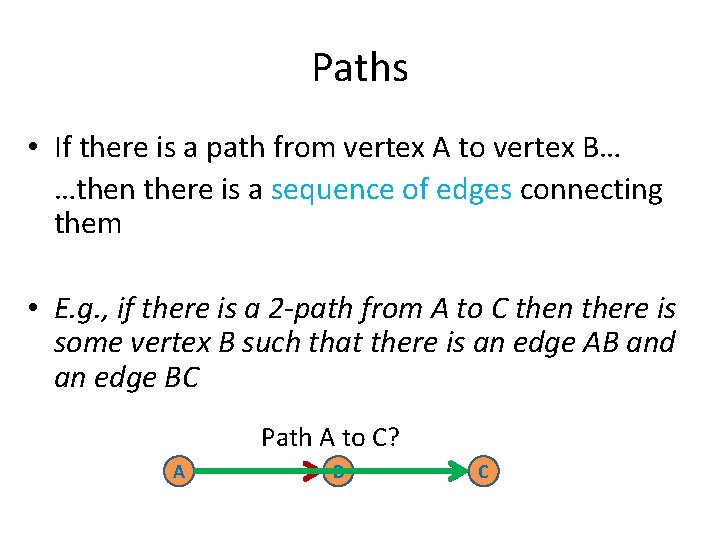
Paths • If there is a path from vertex A to vertex B… …then there is a sequence of edges connecting them • E. g. , if there is a 2 -path from A to C then there is some vertex B such that there is an edge AB and an edge BC Path A to C? A B C

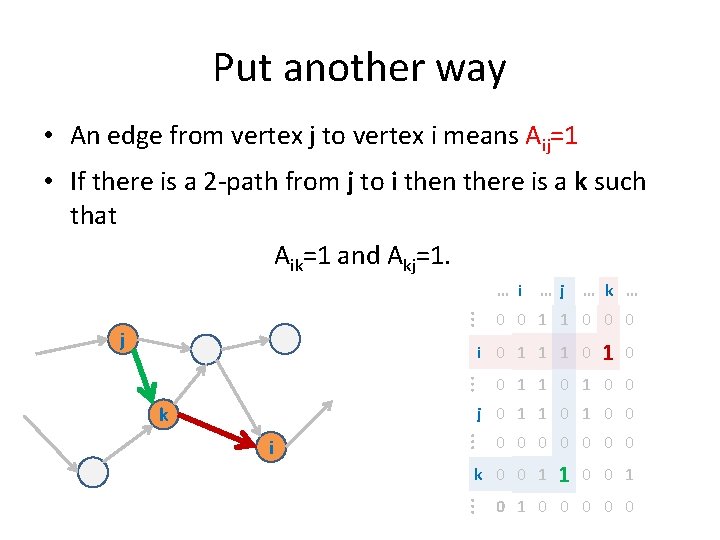
Put another way • An edge from vertex j to vertex i means Aij=1 • If there is a 2 -path from j to i then there is a k such that Aik=1 and Akj=1. … i …j j … k … 0 0 1 1 0 0 0 i 0 1 1 1 0 1 0 0 j 0 1 1 0 0 k i 0 0 0 0 k 0 0 1 1 0 0 0

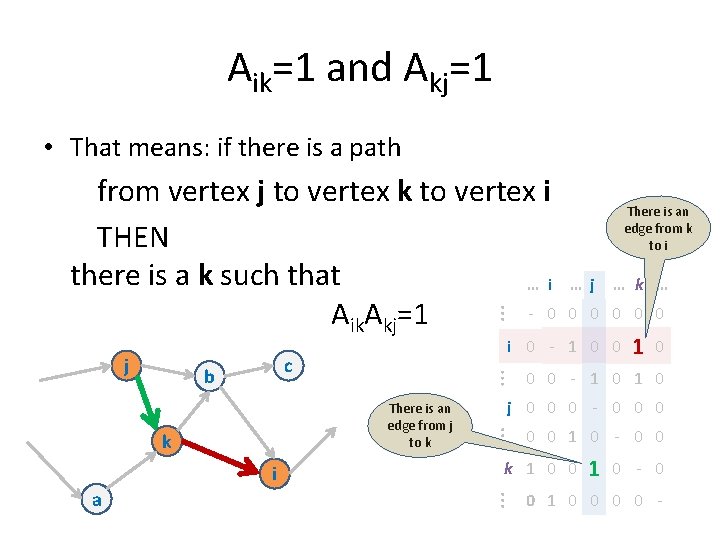
Aik=1 and Akj=1 • That means: if there is a path from vertex j to vertex k to vertex i THEN there is a k such that … i - 0 Aik. Akj=1 c b i 0 0 0 1 0 0 0 - 1 0 0 0 1 0 - 0 0 k 1 0 0 a … k … j 0 0 0 - 0 0 0 There is an edge from j to k k …j i 0 - 1 0 0 j There is an edge from k to i 1 0 - 0 0 1 0 0 -

Another way to see it… • • If vertex j is connected to vertex k AND Vertex I is connected to k THEN Row I will have a 1 in position k AND Column j will have a 1 in position k

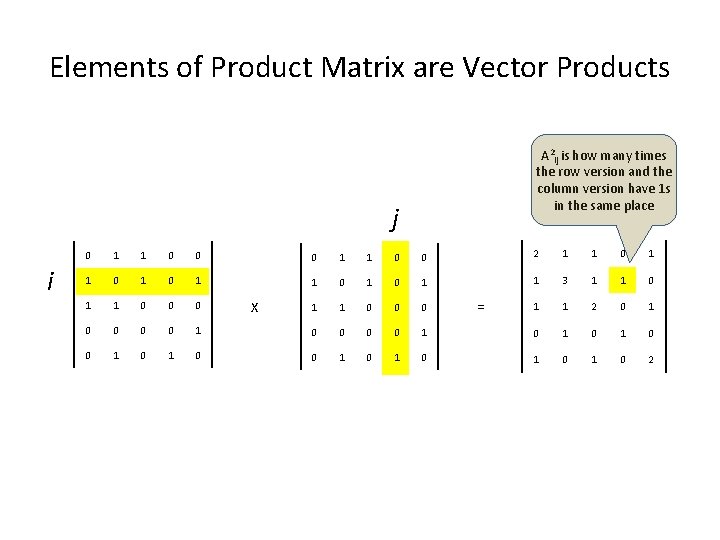
Elements of Product Matrix are Vector Products A 2 ij is how many times the row version and the column version have 1 s in the same place j i 0 1 1 0 0 2 1 1 0 1 0 1 0 1 1 3 1 1 0 0 0 1 1 2 0 1 0 0 0 0 1 0 1 0 1 0 2 X =

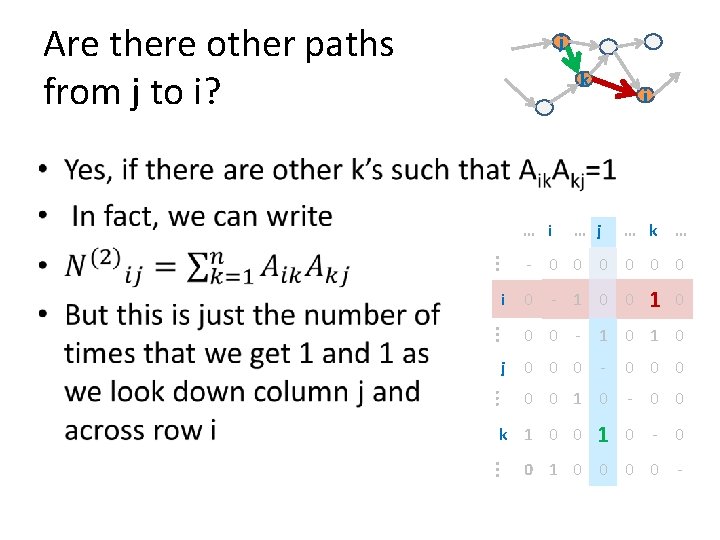
Are there other paths from j to i? j k i • … i i … j … k … - 0 0 0 0 - 1 0 j 0 0 0 - 0 0 0 1 0 - 0 k 1 0 0 0 1 0 0 -

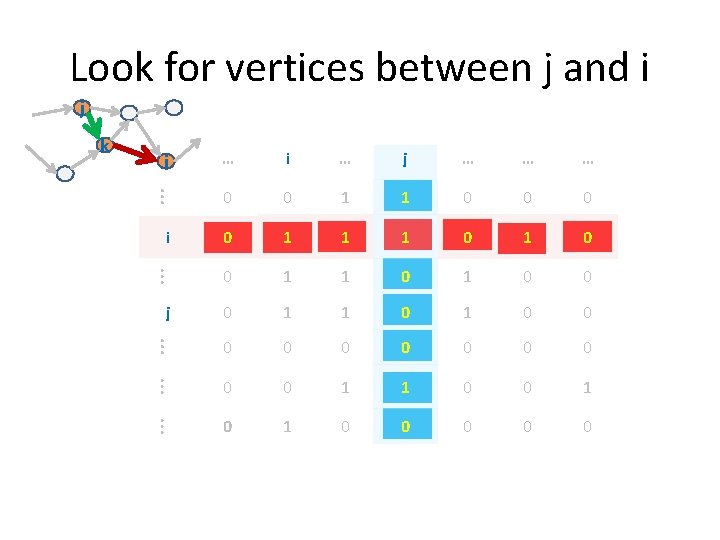
Look for vertices between j and i j i … j … … … 0 0 1 1 0 0 0 i 0 1 1 1 0 1 0 0 j 0 1 1 0 0 0 1 1 0 0 1 k 0 1 0 0 0

Example: Convert 2 -Mode to 1 -Mode(s) 2. Compute transpose of I, IT 1 2 A B 3 C D A B C D 1 1 0 1 1 2 0 1 1 0 3 1 1

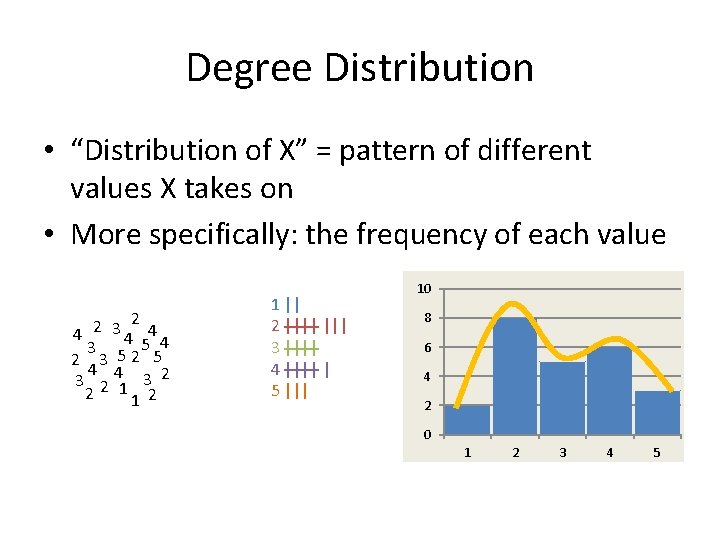
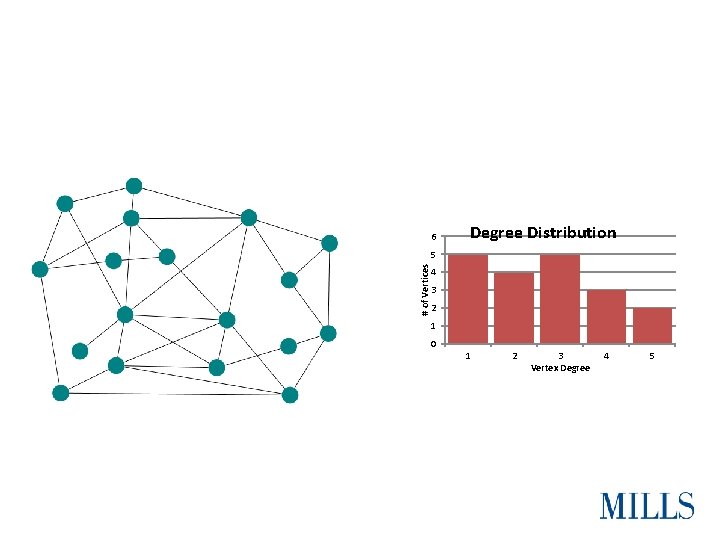
Degree Distribution • “Distribution of X” = pattern of different values X takes on • More specifically: the frequency of each value 2 2 3 4 4 4 3 5 5 4 2 3 2 5 4 3 2 41 3 2 2 1 || 2 |||| 3 |||| 4 |||| | 5 ||| 10 8 6 4 2 0 1 2 3 4 5

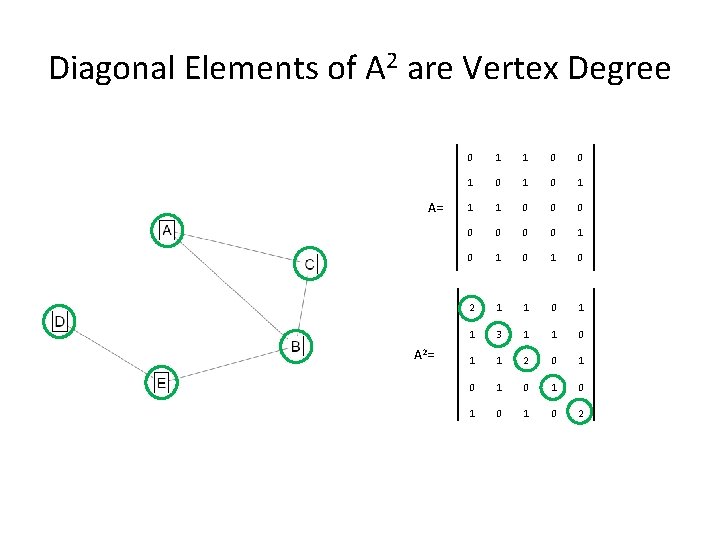
Diagonal Elements of A 2 are Vertex Degree A= A 2= 0 1 1 0 0 1 0 1 1 1 0 0 0 0 1 0 1 0 2 1 1 0 1 1 3 1 1 0 1 1 2 0 1 0 1 0 1 0 2

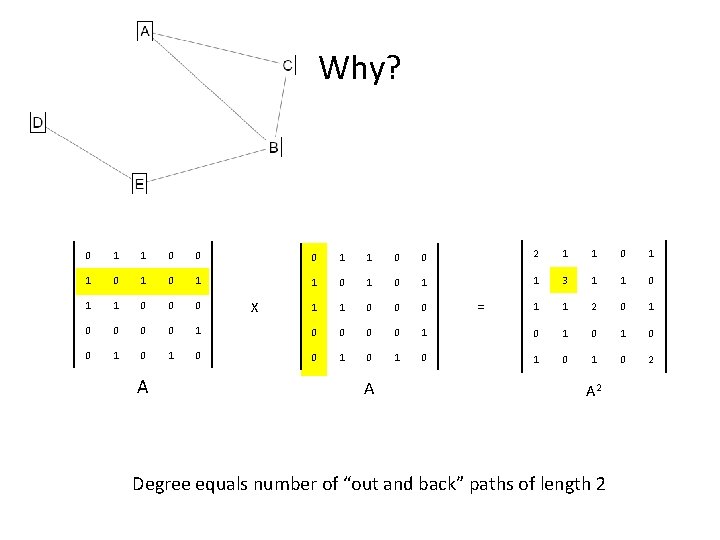
Why? 0 1 1 0 0 2 1 1 0 1 0 1 0 1 1 3 1 1 0 0 0 1 1 2 0 1 0 0 0 0 1 0 1 0 1 0 2 A X A = A 2 Degree equals number of “out and back” paths of length 2

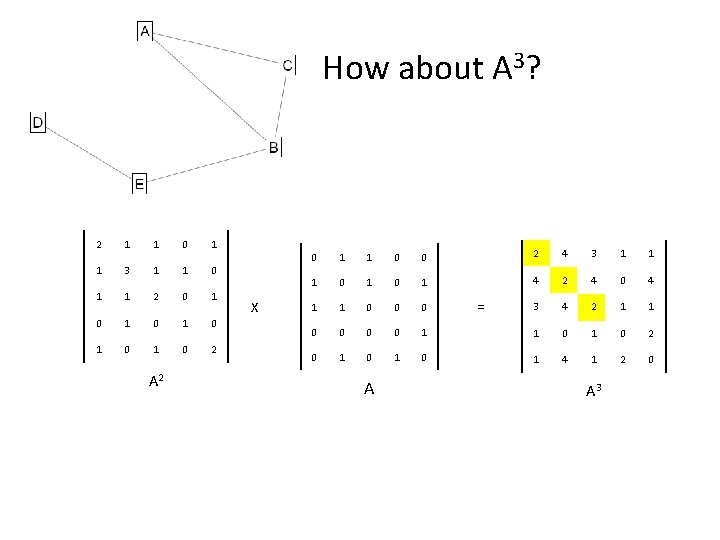
How about A 3? 2 1 1 0 1 1 3 1 1 0 1 1 2 0 1 0 1 0 1 0 2 A 2 X 0 1 1 0 0 2 4 3 1 1 1 0 1 4 2 4 0 4 1 1 0 0 0 3 4 2 1 1 0 0 1 1 0 2 0 1 0 1 4 1 2 0 A = A 3

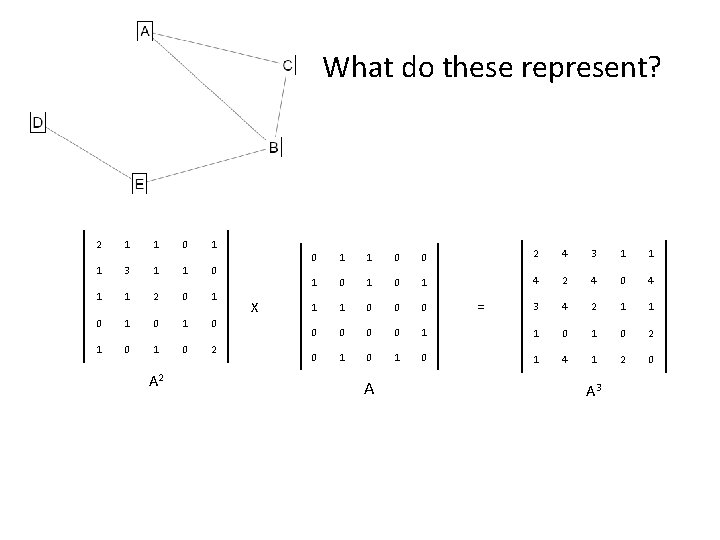
What do these represent? 2 1 1 0 1 1 3 1 1 0 1 1 2 0 1 0 1 0 1 0 2 A 2 X 0 1 1 0 0 2 4 3 1 1 1 0 1 4 2 4 0 4 1 1 0 0 0 3 4 2 1 1 0 0 1 1 0 2 0 1 0 1 4 1 2 0 A = A 3

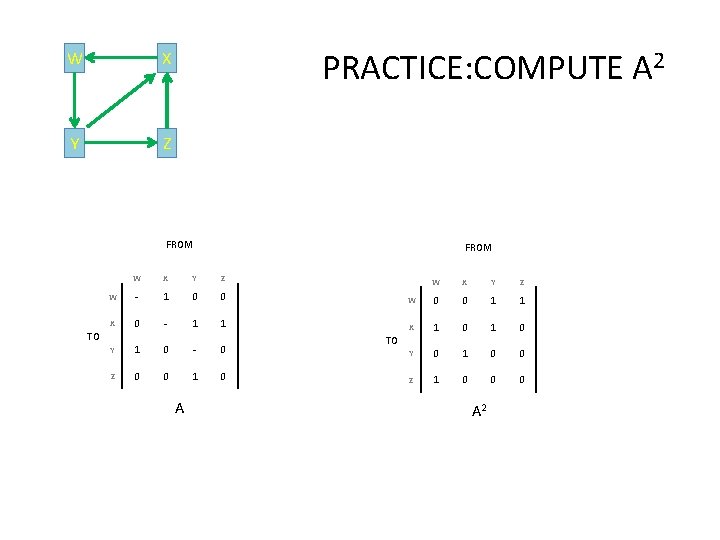
W X Y Z PRACTICE: COMPUTE A 2 FROM W X Y Z W - 1 0 0 X 0 - 1 1 TO Y 1 0 - 0 Z 0 0 1 0 A W X Y Z W 0 0 1 1 X 1 0 Y 0 1 0 0 Z 1 0 0 0 TO A 2

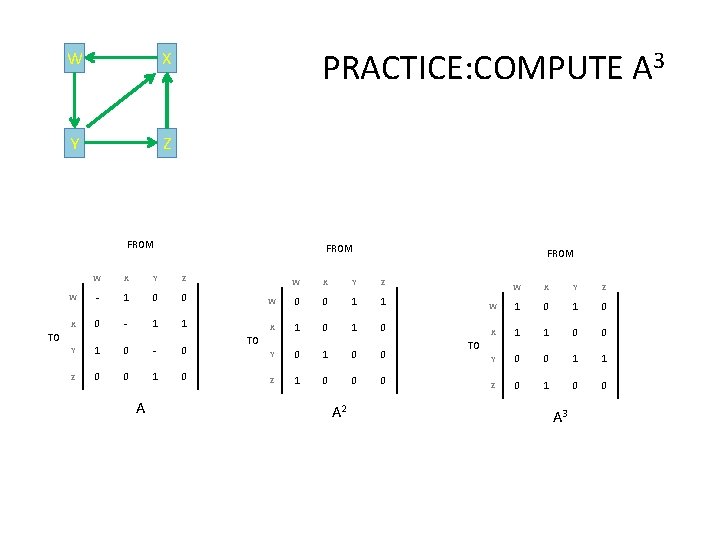
W X Y Z PRACTICE: COMPUTE A 3 FROM W X Y Z W - 1 0 0 X 0 - 1 1 TO Y 1 0 - 0 Z 0 0 1 0 A FROM W X Y Z W 0 0 1 1 X 1 0 TO Y 0 1 0 0 Z 1 0 0 0 A 2 W X Y Z W 1 0 X 1 1 0 0 Y 0 0 1 1 Z 0 1 0 0 TO A 3

6 Degree Distribution # of Vertices 5 4 3 2 1 0 1 2 3 Vertex Degree 4 5

Are there other paths from j to i? • j k i… i …j … k … - 0 0 0 i 0 - 1 0 0 0 - 1 0 j 0 0 0 - 0 0 0 1 0 - 0 0 k 1 0 0 1 0 - 0 0 1 0 0 -