GRAPHS 1 Graph Theory A graph is Mathematically

GRAPHS 1

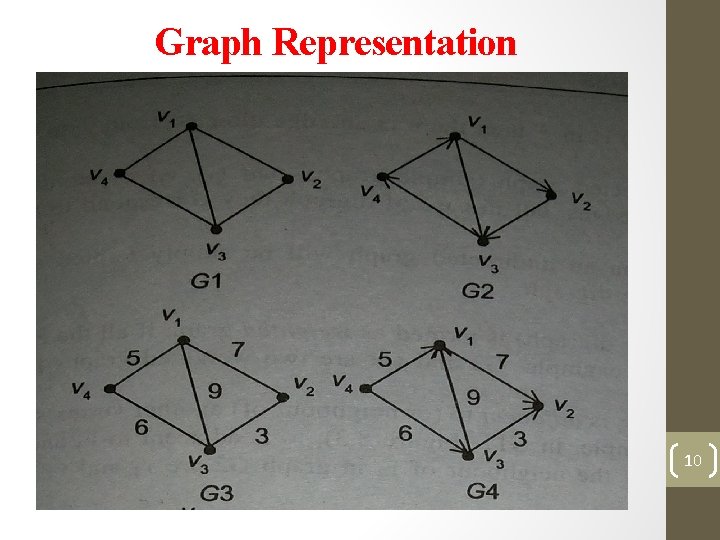
Graph Theory A graph is Mathematically denoted by G= { V, E} Where V= nonempty set of node or Vertices and E= set of edges of the graph. [G 1] • V and E are considered to be finite in number. • Every edge e in Set E associate a pair of nodes of the graph. 2

Graph Terminology Adjacent nodes: Any two nodes which are connected by an edge e in set E in a graph are called adjacent nodes A graph may a directed graph or undirected graph. [G 1] Directed Edge: an edge which is directed from one node to another node is called Directed edge is represented by arrow. [G 2] Undirected Edge: edge which has no specific direction is called undirected edge. Represented using line. [G 1] 3

Graph Terminology Continue… Directed Graph: a graph in which every edge is directed is called digraph. [G 2] Undirected graph: a graph in which every edge is undirected is called undirected graph [G 1] Mixed Graph: if some edges are directed and some are undirected then graph is called mixed graph. Initial node and Terminating node: in directed graph if edge e between pair of node {x, y} then node x is called initial node and y is called terminating node 4

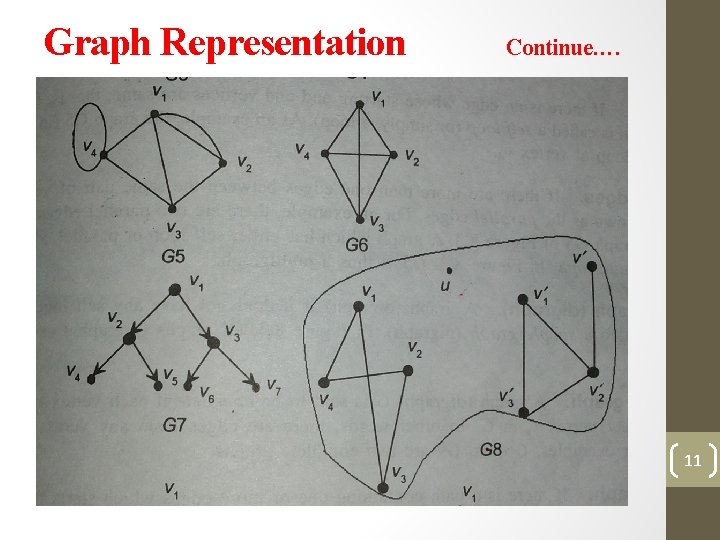
Graph Terminology Loop: Continue… an edge in graph which initiate from the node and terminating at same node then it is called loop. [G 5] Loop at least contain one node. Distinct Edges: in directed graph, two edges between a pair of nodes and in opposite direction are distinct edges. Parallel Edges: if pair of nodes joined by more than one edges than edges are called parallel edges. [G 5] those 5

Graph Terminology Continue… Multigraph: if graph contain some parallel edges is called multi graph. Simple Graph: if there is no more than one edge between a pair of nodes then such graph is called the simple graph. Weighted Graph: a graph in which weights are assigned to every edge is called a weighted graph. [G 3, G 4] isolated node: a node which is not adjacent to any other node in the graph is called an isolated node. [G 8] 6

Graph Terminology Continue… Null Graph: a graph contain only the isolated nodes is called the null graph. Out degree of a node: set of edges for any node X which has X as initiator node called the out degree of node X [G 4] In degree of a node: set of edges for any node X which has X as terminator node called the in degree of node X [G 4] Total degree: the some of in degree and out degree of node X is called the total degree of node X. [G 4] 7

Graph Terminology Continue… Total Degree of node in Undirected graph: The number of edges incident to a node X is called the total degree of node X. Path: a path is said to be sequence of edges such that originating in the initial node of the first edge and ending in the terminating node of the last edge in the sequence. Length of Path: of a path. the number of edges appearing in the sequence 8

Graph Terminology Continue… Simple Path: if number of edges are distinct in given path then it is called the simple path. OR A Graph if it does not have any self loop or parallel edges is called simple graph) Elementary Path: a path in which all the nodes through which it traverse are distinct than it is elementary path. Any path which is not elementary contains cycle. Acyclic Graph: a simple diagraph which does not contain any cycle is called the acyclic. 9

Graph Representation 10

Graph Representation Continue…. 11

Graph Representation Continue…. 12

Graph Traversal Two Traversals: DFS : Depth First Search BFS : Breadth First Search DFS: • Traversing a graph using the DFS algorithm requires to visit each node only once in down word starting from the root node. • Each node is visited only once and it is marked as visited. • We follow single root in traversing un till that node have no single node remained to be visited. • Once we reach the node which has no child node then we backtrack our process to parent node of that node and continue our process in other available direction i. e. the search returns to the last node which still has unmarked adjacent nodes and continue marking untill all nodes are marked. 13

Graph Traversal Process : DFS (Recursive) Visit Node X Visit left child of node X Visit Right Child of node X • Apply above three steps recursively un till all nodes get visited starting from root node. • DFS use Stack Data structures. 14

Graph Traversal BFS: BFS require node and it successors at the same level visited immediately. BFS visit each node only once and marked as visited only when it successor are visited. Process : BFS 1. let L be the traversed list (just like variable). it is initially empty. 2. start with root node and add it to list L. 3. visit its successors and add them to end of the list. 4. Pick next node in the list L and visit its successors and add them to end of the list. 5. Repeat above process un till all the nodes from all the levels are visited in this fashion. 6. The sequence in list L gives u a traversing sequence. 15

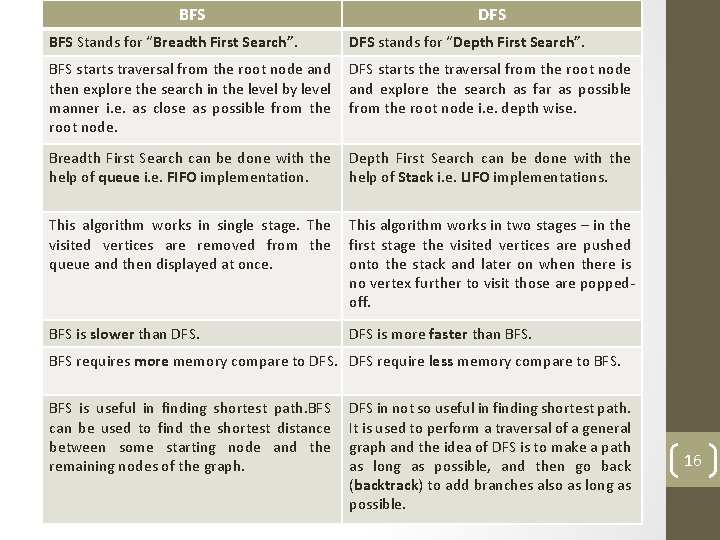
BFS Stands for “Breadth First Search”. DFS stands for “Depth First Search”. DFSBFS starts the traversal from the root node Difference Between and DFS BFS starts traversal from the root node and then explore the search in the level by level manner i. e. as close as possible from the root node. and explore the search as far as possible from the root node i. e. depth wise. Breadth First Search can be done with the help of queue i. e. FIFO implementation. Depth First Search can be done with the help of Stack i. e. LIFO implementations. This algorithm works in single stage. The visited vertices are removed from the queue and then displayed at once. This algorithm works in two stages – in the first stage the visited vertices are pushed onto the stack and later on when there is no vertex further to visit those are poppedoff. BFS is slower than DFS is more faster than BFS requires more memory compare to DFS require less memory compare to BFS is useful in finding shortest path. BFS can be used to find the shortest distance between some starting node and the remaining nodes of the graph. DFS in not so useful in finding shortest path. It is used to perform a traversal of a general graph and the idea of DFS is to make a path as long as possible, and then go back (backtrack) to add branches also as long as possible. 16

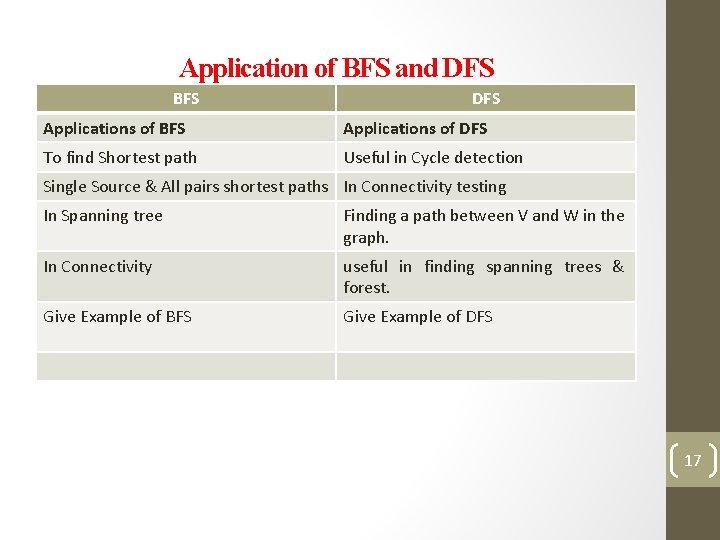
Application of BFS and DFS BFS DFS Applications of BFS Applications of DFS To find Shortest path Useful in Cycle detection Single Source & All pairs shortest paths In Connectivity testing In Spanning tree Finding a path between V and W in the graph. In Connectivity useful in finding spanning trees & forest. Give Example of BFS Give Example of DFS 17