Graphing Rational Functions A rational function is a

Graphing Rational Functions

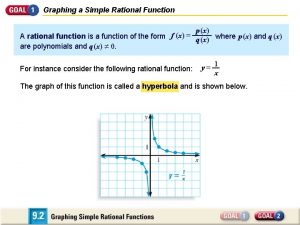
A rational function is a function of the form f(x) = where P(x) and Q(x) are polynomials and Q(x) = 0. Example: f (x) = f(x) = , is defined for all real numbers except x = 0. x f(x) 2 0. 5 -2 -0. 5 1 1 -1 -1 0. 5 2 -0. 5 -2 0. 1 10 -0. 1 -10 0. 01 100 -0. 01 -100 0. 001 1000 -0. 001 -1000 As x → 0+, f(x) → +∞. As x → 0–, f(x) → -∞. 2

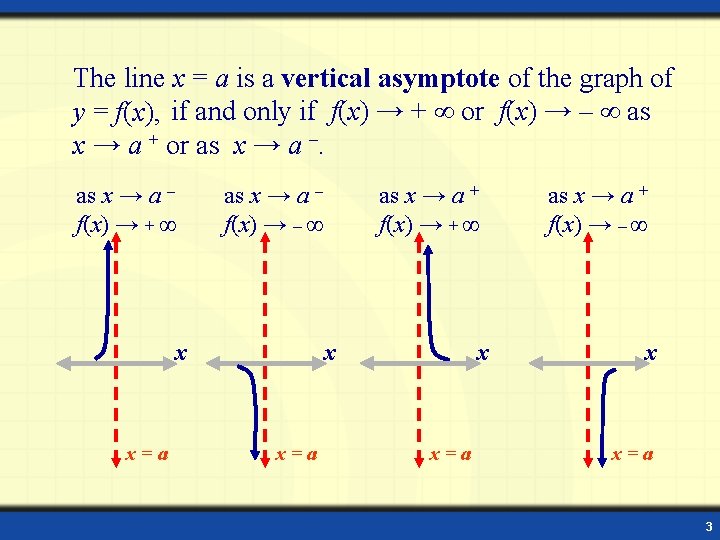
The line x = a is a vertical asymptote of the graph of y = f(x), if and only if f(x) → + ∞ or f(x) → – ∞ as x → a + or as x → a – f(x) → + ∞ as x → a – f(x) → – ∞ x x x=a as x → a + f(x) → + ∞ x=a x x=a as x → a + f(x) → – ∞ x x=a 3

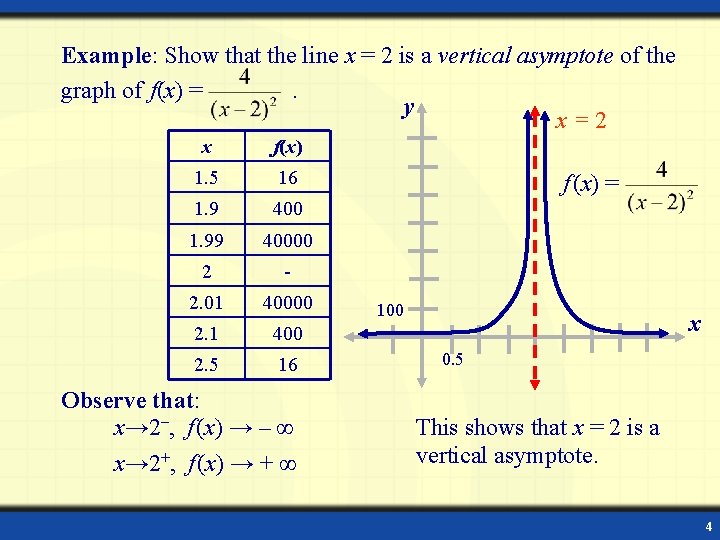
Example: Show that the line x = 2 is a vertical asymptote of the graph of f(x) =. y x=2 x f(x) 1. 5 16 1. 9 400 1. 99 40000 2 - 2. 01 40000 2. 1 400 2. 5 16 Observe that: x→ 2–, f (x) → – ∞ x→ 2+, f (x) → + ∞ f (x) = 100 x 0. 5 This shows that x = 2 is a vertical asymptote. 4

A rational function may have a vertical asymptote at x = a for any value of a such that Q(a) = 0. Example: Find the vertical asymptotes of the graph of f(x) = . Set the denominator equal to zero and solve. Solve the quadratic equation x 2 + 4 x – 5. (x – 1)(x + 5) = 0 Therefore, x = 1 and x = -5 are the values of x for which f may have a vertical asymptote. As x → 1– , f(x) → – ∞. As x → -5–, f(x) → + ∞. As x → 1+, f(x) → + ∞. As x →-5+, f(x) → – ∞. x = 1 is a vertical asymptote. x = -5 is a vertical asymptote. 5

Example: Find the vertical asymptotes of the graph of f(x) = . 1. Find the roots of the denominator. 0 = x 2 – 4 = (x + 2)(x – 2) Possible vertical asymptotes are x = -2 and x = +2. 2. Calculate the values approaching -2 and +2 from both sides. x → -2, f(x) → -0. 25; so x = -2 is not a vertical asymptote. x → +2–, f(x) → – ∞ and x →+2+, f(x) → + ∞. y So, x = 2 is a vertical asymptote. x=2 f is undefined at -2 A hole in the graph of f at (-2, -0. 25) shows a removable singularity. (-2, -0. 25) x 6

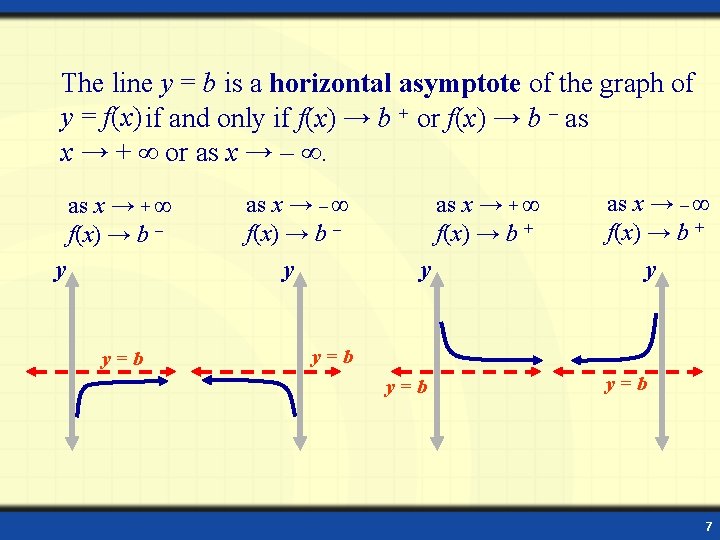
The line y = b is a horizontal asymptote of the graph of y = f(x) if and only if f(x) → b + or f(x) → b – as x → + ∞ or as x → – ∞. as x → + ∞ f(x) → b – y as x → – ∞ f(x) → b – y y=b as x → + ∞ f(x) → b + y as x → – ∞ f(x) → b + y y=b y=b 7

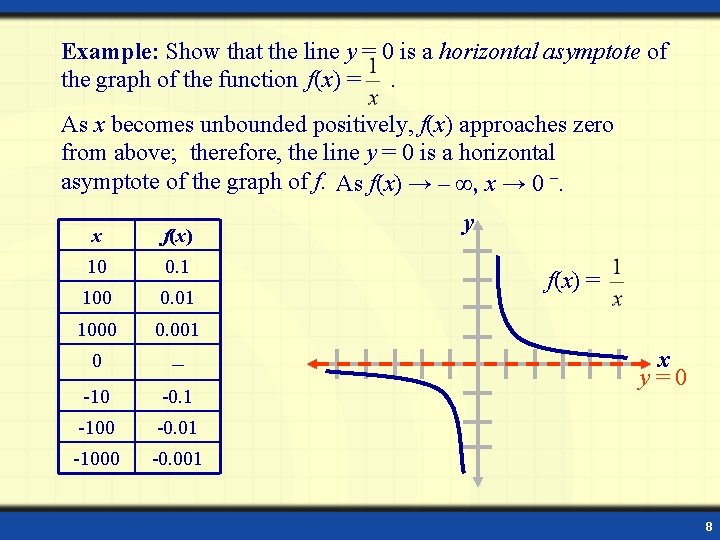
Example: Show that the line y = 0 is a horizontal asymptote of the graph of the function f(x) =. As x becomes unbounded positively, f(x) approaches zero from above; therefore, the line y = 0 is a horizontal asymptote of the graph of f. As f(x) → – ∞, x → 0 –. x f(x) 10 0. 1 100 0. 01 1000 0. 001 0 – -10 -0. 1 -100 -0. 01 -1000 -0. 001 y f(x) = x y=0 8

Example: Determine the horizontal asymptotes of the graph of f(x) =. Divide x 2 + 1 into x 2. As x → +∞, f(x) = 1 – → 0– ; so, f(x) = 1 – Similarly, as x → – ∞, f(x) → 1–. Therefore, the graph of f has y = 1 as a horizontal asymptote. → 1 –. y y=1 x 9

Finding Asymptotes for Rational Functions Given a rational function: f (x) = P(x) Q(x) = am xm + lower degree terms bn xn + lower degree terms • If c is a real number which is a root of both P(x) and Q(x), then there is a removable singularity at c. • If c is a root of Q(x) but not a root of P(x), then x = c is a vertical asymptote. • If m > n, then there are no horizontal asymptotes. • If m < n, then y = 0 is a horizontal asymptote. • If m = n, then y = am is a horizontal asymptote. bn 10

Example: Find all horizontal and vertical asymptotes of f (x) = . Factor the numerator and denominator. The only root of the numerator is x = -1. The roots of the denominator are x = -1 and x = 2. x=2 Since -1 is a common root of both, there y is a hole in the graph at -1. Since 2 is a root of the denominator but not the numerator, x = 2 will be a vertical asymptote. y=3 x Since the polynomials have the same degree, y = 3 will be a horizontal asymptote. 11

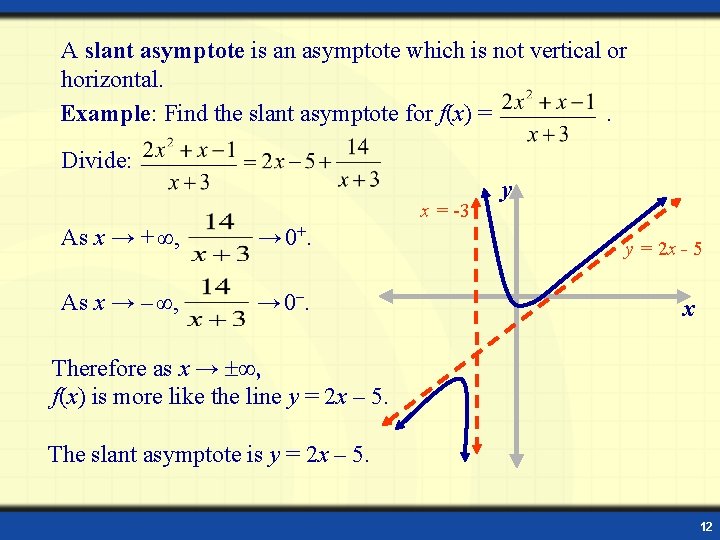
A slant asymptote is an asymptote which is not vertical or horizontal. Example: Find the slant asymptote for f(x) =. Divide: x = -3 As x → + ∞, → 0+. As x → – ∞, → 0–. y y = 2 x - 5 x Therefore as x → ∞, f(x) is more like the line y = 2 x – 5. The slant asymptote is y = 2 x – 5. 12