Graphing Quadratic Functions MA 912 A 7 1






- Slides: 14

Graphing Quadratic Functions MA. 912. A. 7. 1 Graph quadratic equations. MA. 912. A. 7. 6 Identify the axis of symmetry, vertex, domain, range, and intercept(s) for a given parabola

Quadratic Function y = ax 2 + bx + c Quadratic Term Linear Term Constant Term 2 What is the linear term of y = 4 x – 3? 0 x 2 What is the linear term of y = x - 5 x ? -5 x What is the constant term of y = x 2 – 5 x? 0 Can the quadratic term be zero? No!

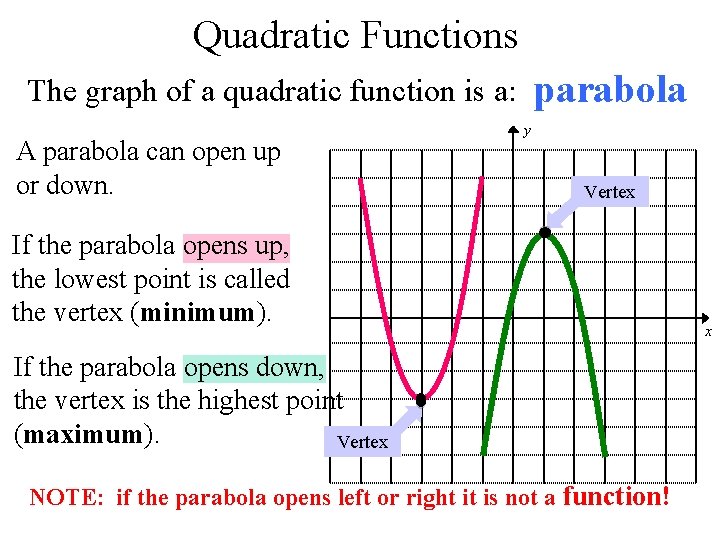
Quadratic Functions parabola The graph of a quadratic function is a: A parabola can open up or down. y Vertex If the parabola opens up, the lowest point is called the vertex (minimum). If the parabola opens down, the vertex is the highest point (maximum). Vertex NOTE: if the parabola opens left or right it is not a function! x

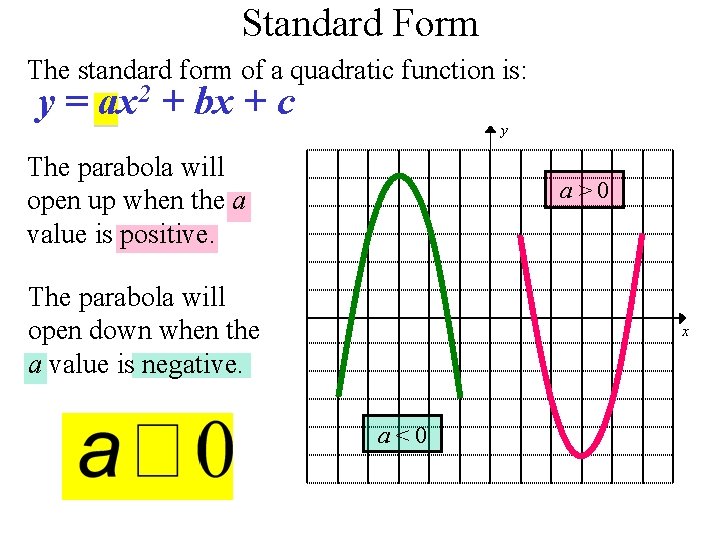
Standard Form The standard form of a quadratic function is: y = ax 2 + bx + c y The parabola will open up when the a value is positive. a>0 The parabola will open down when the a value is negative. x a<0

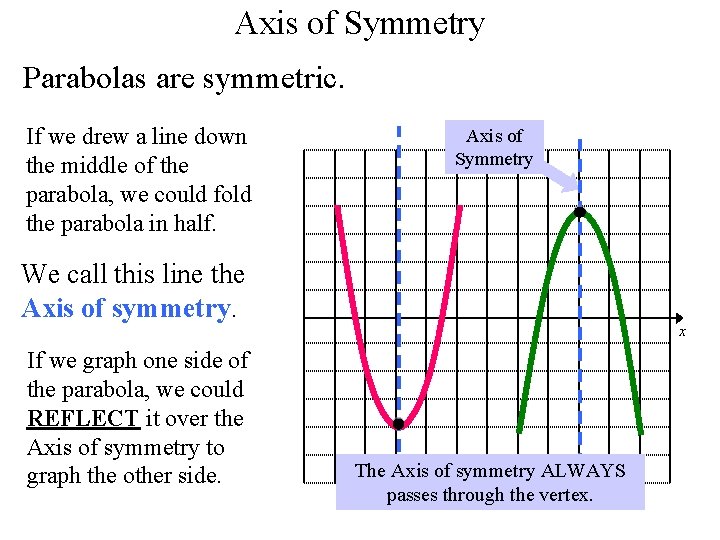
Axis of Symmetry Parabolas are symmetric. If we drew a line down the middle of the parabola, we could fold the parabola in half. Axisy of Symmetry We call this line the Axis of symmetry. x If we graph one side of the parabola, we could REFLECT it over the Axis of symmetry to graph the other side. The Axis of symmetry ALWAYS passes through the vertex.

Finding the Axis of Symmetry When a quadratic function is in standard form y = ax 2 + bx + c, the equation of the Axis of symmetry is This is best read as … ‘the opposite of b divided by the quantity of 2 times a. ’ Find the Axis of symmetry for y = 3 x 2 – 18 x + 7 a = 3 b = -18 The Axis of symmetry is x = 3.

Finding the Vertex The Axis of symmetry always goes through the Vertex Thus, the Axis of symmetry gives _______. X-coordinate of the vertex. us the ______ Find the vertex of y = -2 x 2 + 8 x - 3 STEP 1: Find the Axis of symmetry a = -2 b=8 The xcoordinate of the vertex is 2

Finding the Vertex Find the vertex of y = -2 x 2 + 8 x - 3 STEP 1: Find the Axis of symmetry STEP 2: Substitute the x – value into the original equation to find the y –coordinate of the vertex. The vertex is (2 , 5)

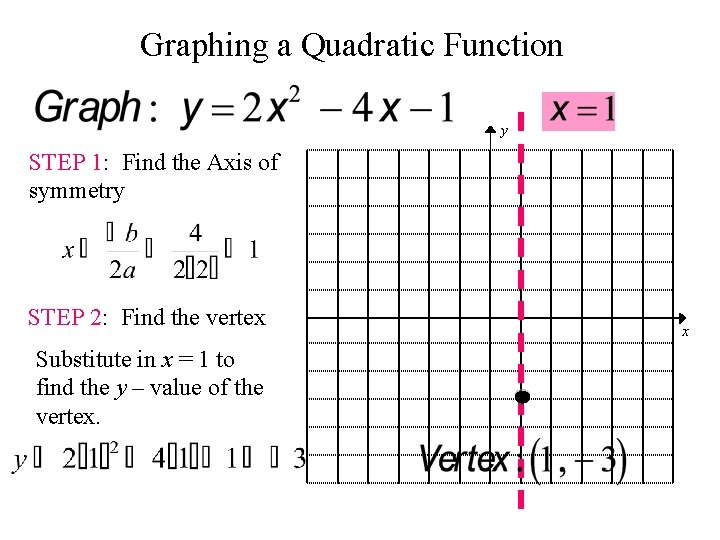
Graphing a Quadratic Function There are 3 steps to graphing a parabola in standard form. STEP 1: Find the Axis of symmetry using: STEP 2: Find the vertex STEP 3: Find two other points and reflect them across the Axis of symmetry. Then connect the five points with a smooth curve. MAKE A TABLE using x – values close to the Axis of symmetry.

Graphing a Quadratic Function y STEP 1: Find the Axis of symmetry STEP 2: Find the vertex Substitute in x = 1 to find the y – value of the vertex. x

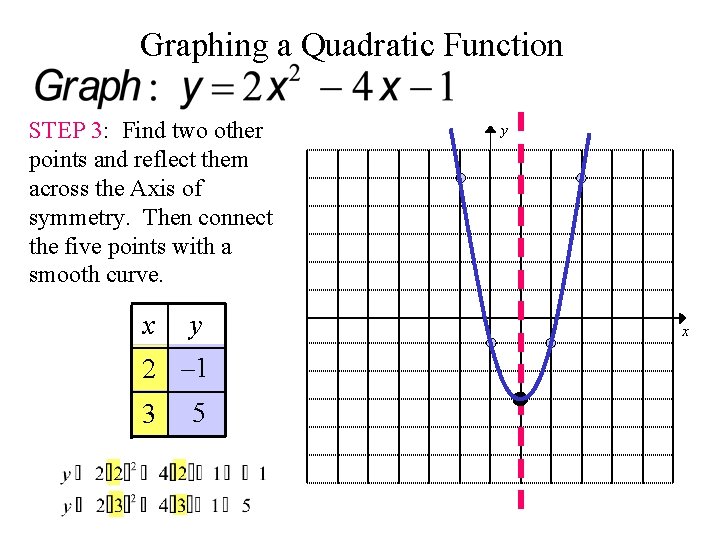
Graphing a Quadratic Function STEP 3: Find two other points and reflect them across the Axis of symmetry. Then connect the five points with a smooth curve. x y 2 – 1 3 5 y x

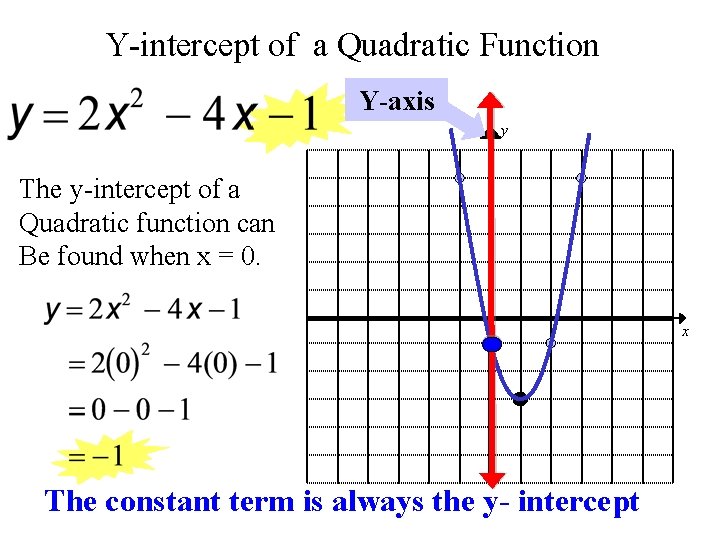
Y-intercept of a Quadratic Function Y-axis y The y-intercept of a Quadratic function can Be found when x = 0. x The constant term is always the y- intercept

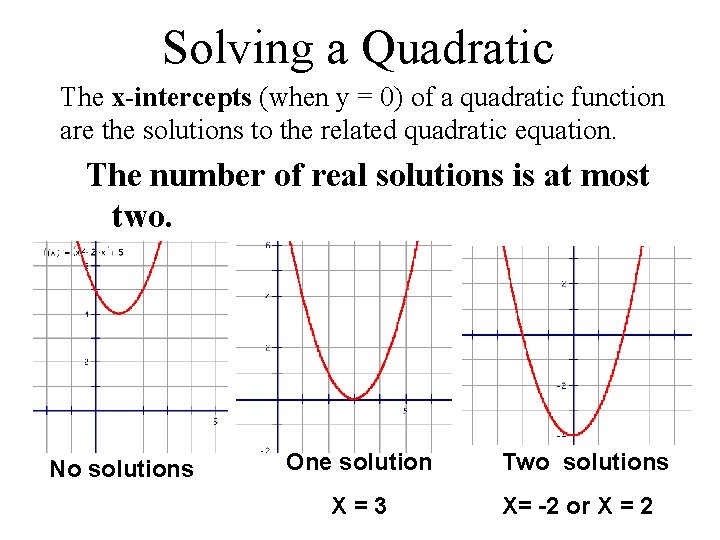
Solving a Quadratic The x-intercepts (when y = 0) of a quadratic function are the solutions to the related quadratic equation. The number of real solutions is at most two. No solutions One solution X=3 Two solutions X= -2 or X = 2

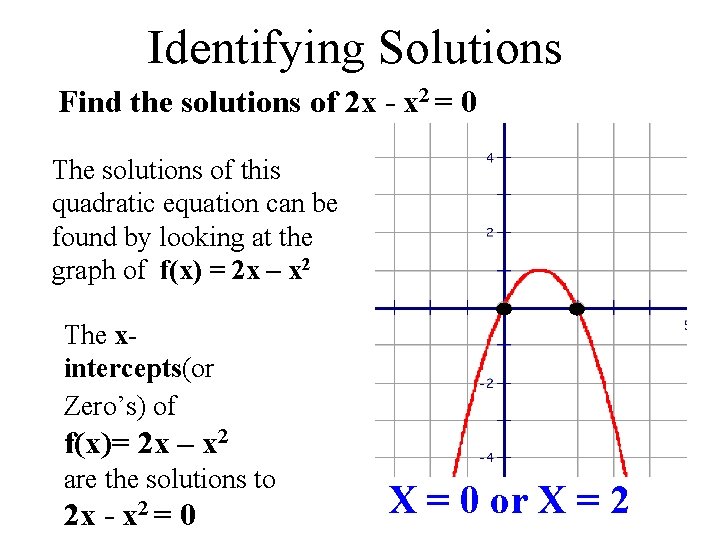
Identifying Solutions Find the solutions of 2 x - x 2 = 0 The solutions of this quadratic equation can be found by looking at the graph of f(x) = 2 x – x 2 The xintercepts(or Zero’s) of f(x)= 2 x – x 2 are the solutions to 2 x - x 2 = 0 X = 0 or X = 2