Graphing Quadratic Functions General Form It is assumed








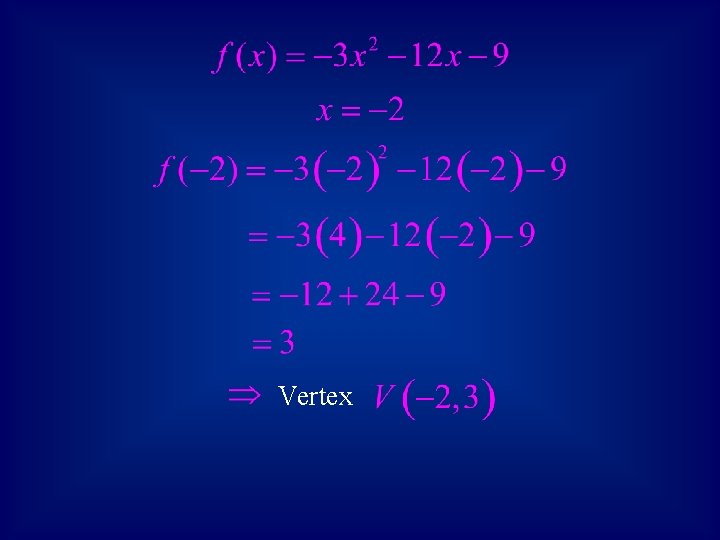



- Slides: 14

Graphing Quadratic Functions – General Form • It is assumed that you have already viewed the previous three slide shows titled Graphing Quadratic Functions – Concept Graphing Quadratic Functions – Standard Form Graphing Quadratic Functions – Converting General Form To Standard Form • The next three pages are summaries from those shows, and are important to understanding this module.

Standard Form of a Quadratic Function General Form of a Quadratic Function

Graphing a Quadratic Function in Standard Form Face Up Face Down Narrow Wide Vertex Axis of symmetry

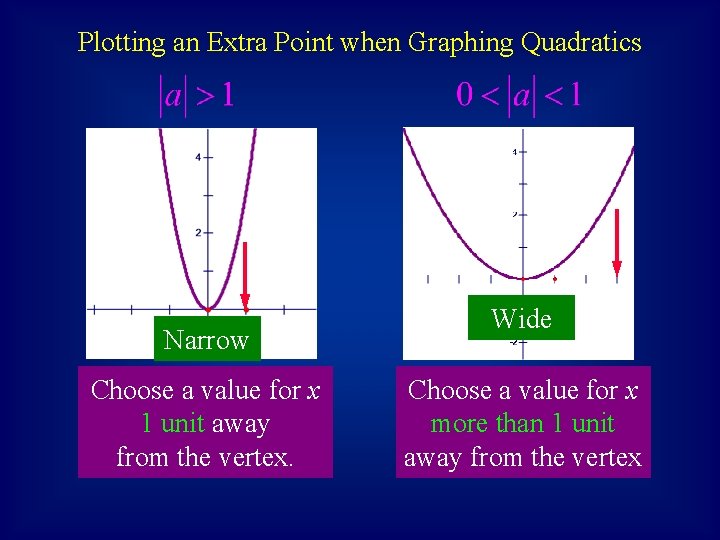
Plotting an Extra Point when Graphing Quadratics Narrow Choose a value for x 1 unit away from the vertex. Wide Choose a value for x more than 1 unit away from the vertex

Vertex of the Graph of a Quadratic Function in General Form • Given the general form of a quadratic function … …the x-value of the vertex is given by

• There are two other helpful concepts for graphing a quadratic function that is in general form. • Concept 1: We already know that the x-value of the vertex is given by … The y-value of the vertex is given by …

Thus, the vertex of the graph of the quadratic function in general form is given by • Concept 2: The a of the general form is the same value as the a in the standard form. This means that the a in the general form can be used to determine the face up/face down and narrow/wide behavior, just as it did in the standard form.

Summary for Graphing Quadratics in General Form Face Up Vertex Face Down Narrow Wide Axis of symmetry

• Example: Sketch the graph of the given quadratic function. Face down Narrow Vertex:
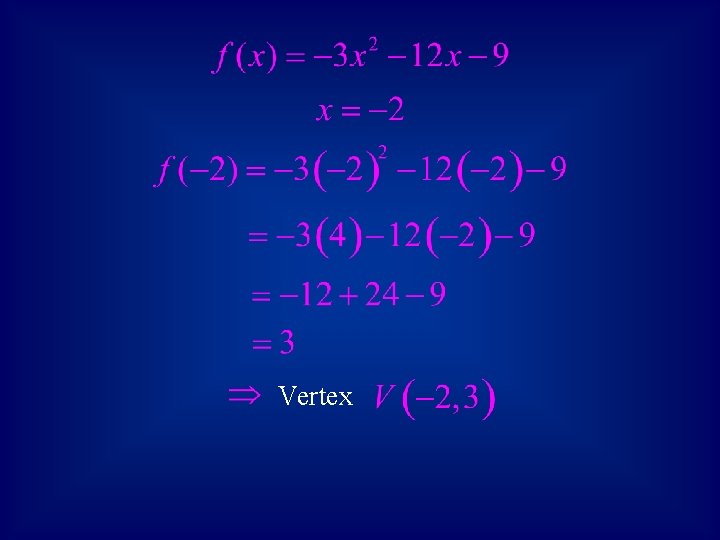
Vertex

Axis of Symmetry: x = x-value of vertex Point: since the parabola is narrow, use an x-value that is only one unit from the vertex.

Summary: Function: Face down Narrow Axis: Point:

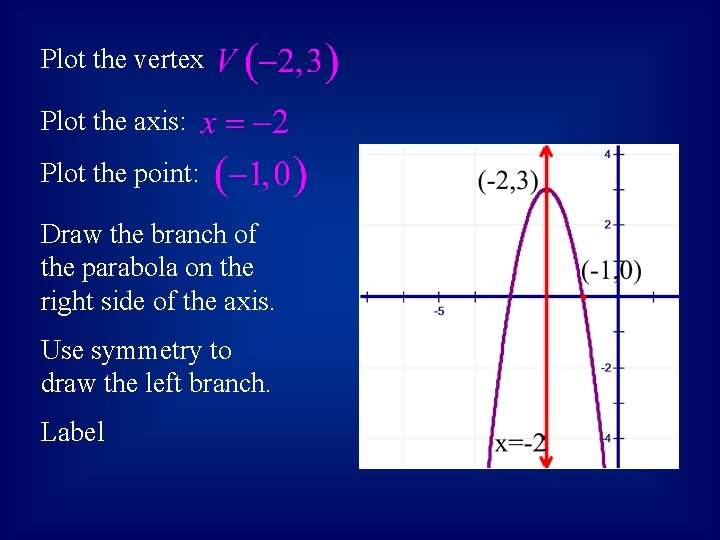
Plot the vertex Plot the axis: Plot the point: Draw the branch of the parabola on the right side of the axis. Use symmetry to draw the left branch. Label
