Graphing Quadratic Equations a stepbystep guide with practice

Graphing Quadratic Equations a step-by-step guide with practice

Graphing from Standard Form l Graph y = x 2 – 6 x + 8.

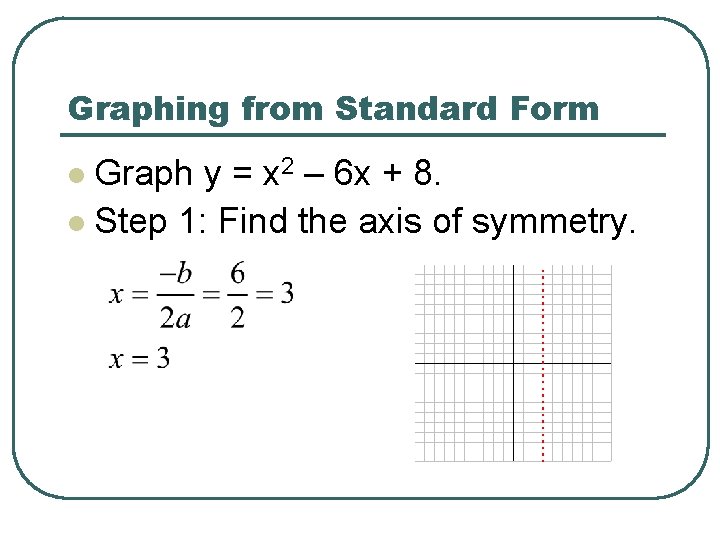
Graphing from Standard Form Graph y = x 2 – 6 x + 8. l Step 1: Find the axis of symmetry. l

Graphing from Standard Form Graph y = x 2 – 6 x + 8. l Step 2: Find the vertex. l l Vertex: (3, – 1)

Graphing from Standard Form Graph y = x 2 – 6 x + 8. l Step 3: Graph using quadratic pattern. l

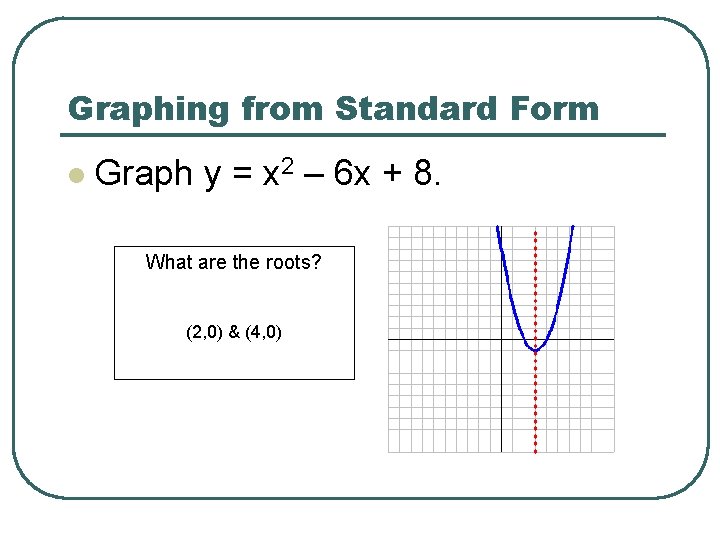
Graphing from Standard Form l Graph y = x 2 – 6 x + 8. What are the roots? (2, 0) & (4, 0)

Graphing from Intercept Form l Graph y = (x – 4)(x + 2).

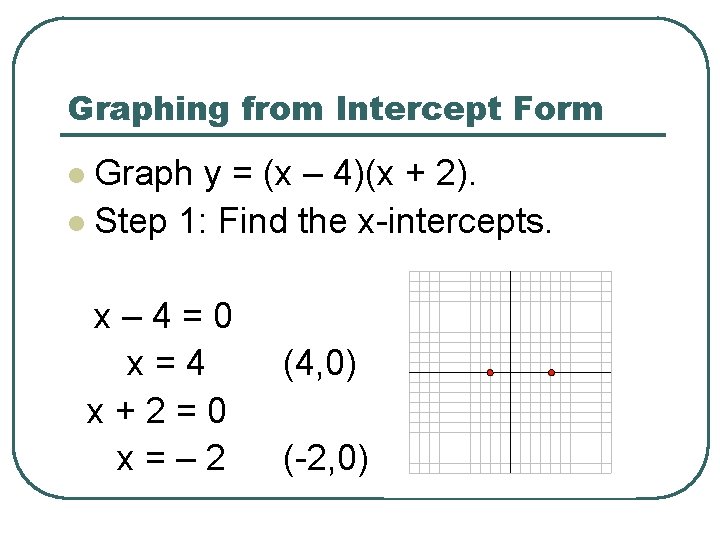
Graphing from Intercept Form Graph y = (x – 4)(x + 2). l Step 1: Find the x-intercepts. l x– 4=0 x=4 x+2=0 x=– 2 (4, 0) (-2, 0)

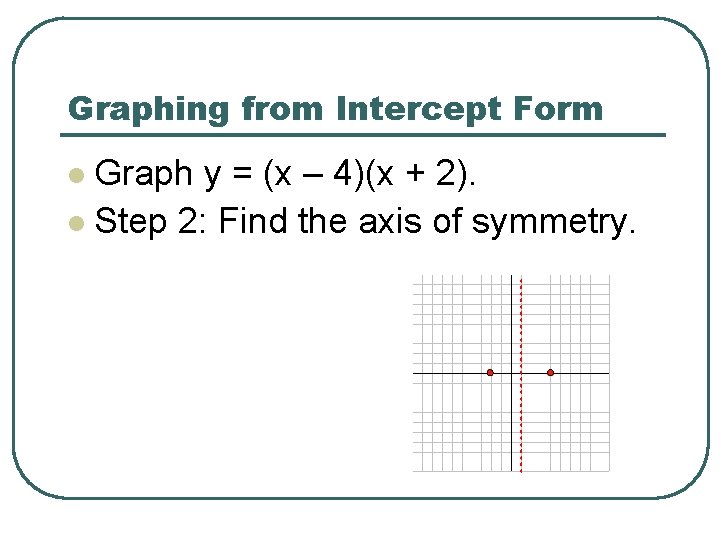
Graphing from Intercept Form Graph y = (x – 4)(x + 2). l Step 2: Find the axis of symmetry. l

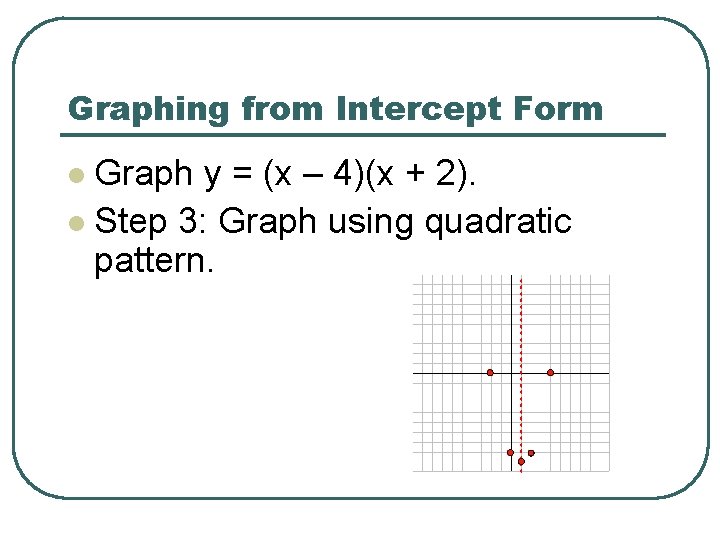
Graphing from Intercept Form Graph y = (x – 4)(x + 2). l Step 3: Graph using quadratic pattern. l

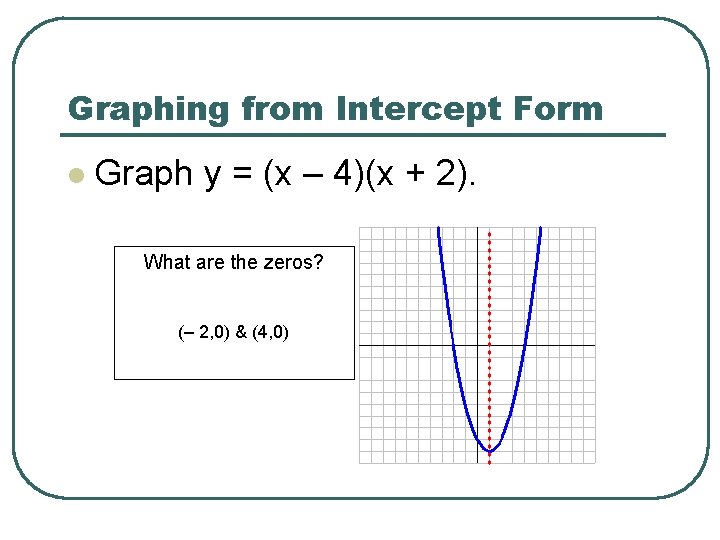
Graphing from Intercept Form l Graph y = (x – 4)(x + 2). What are the zeros? (– 2, 0) & (4, 0)

Graphing from Vertex Form l Graph y = 2(x – 1)2 + 3

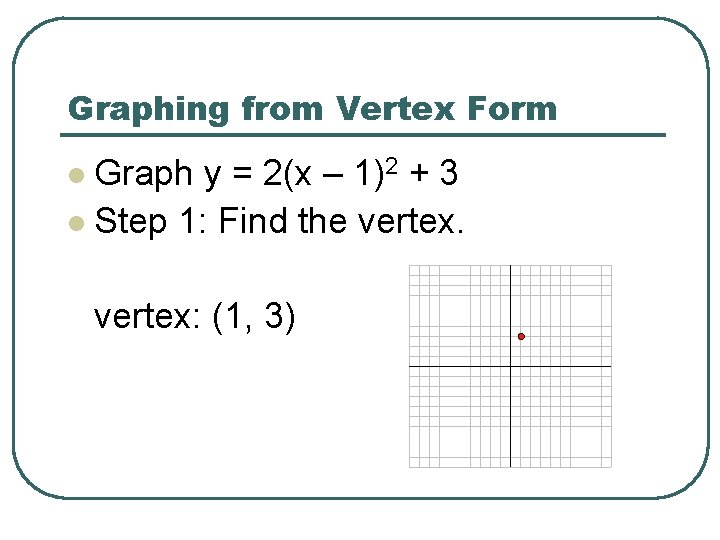
Graphing from Vertex Form Graph y = 2(x – 1)2 + 3 l Step 1: Find the vertex. l vertex: (1, 3)

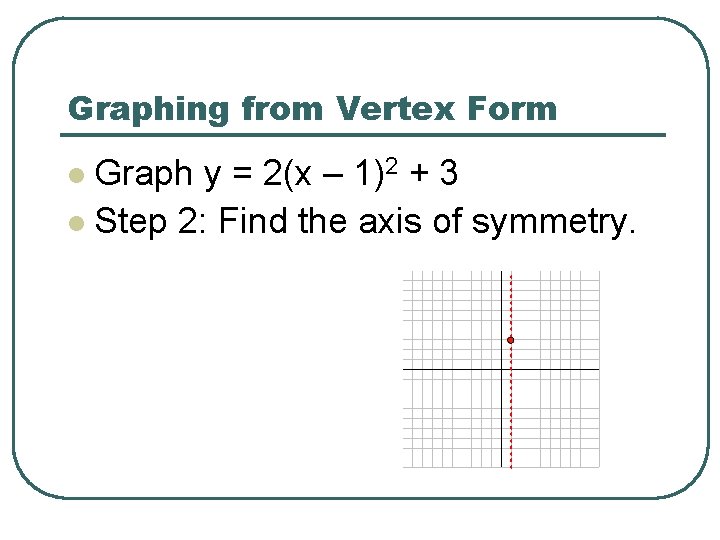
Graphing from Vertex Form Graph y = 2(x – 1)2 + 3 l Step 2: Find the axis of symmetry. l

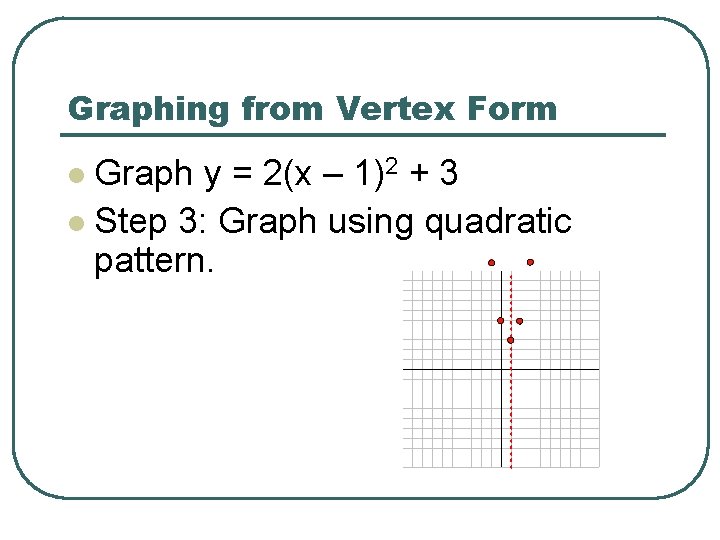
Graphing from Vertex Form Graph y = 2(x – 1)2 + 3 l Step 3: Graph using quadratic pattern. l

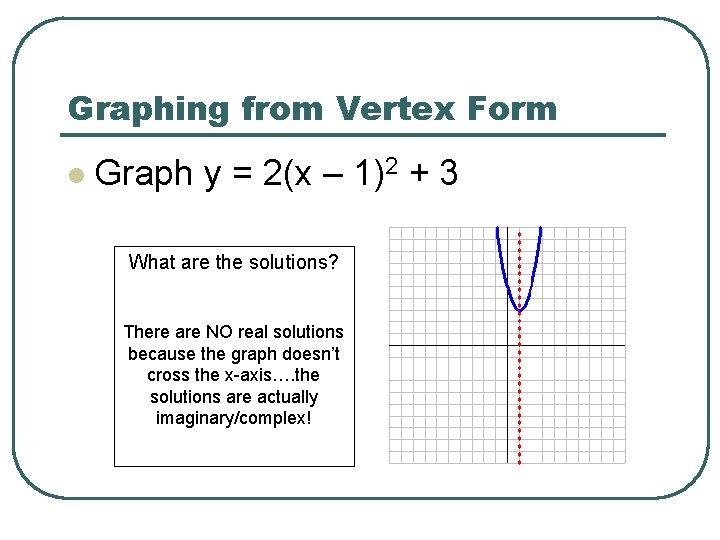
Graphing from Vertex Form l Graph y = 2(x – 1)2 + 3 What are the solutions? There are NO real solutions because the graph doesn’t cross the x-axis…. the solutions are actually imaginary/complex!